1．已知集合 $ A=｛x|-1 < x < 1｝ $ ， $ B=｛x|0\leqslant x\leqslant 2｝ $ ，则 $ A\cup B= $ （ ）
A． $ ｛x|-1 < x < 2｝ $
B． $ ｛x|-1 < x\leqslant 2｝ $
C． $ ｛x|0\leqslant x < 1｝ $
D． $ ｛x|0\leqslant x\leqslant 2｝ $
因为 $ A=｛x|-1 < x < 1｝ $ ， $ B=｛x|0\leqslant x\leqslant 2｝ $ ，所以 $ A\cup B=｛x|-1 < x\leqslant 2｝ $ .故选 $ \mathrm{B} $ .
2．已知 $ A\cup B=｛x\in \boldsymbol{N}|1\leqslant x\leqslant 6｝ $ ，集合 $ A=｛1,3,5,6｝ $ ，则集合 $ B $ 可以是（ ）
A． $ ｛1,2｝ $
B． $ ｛4,5｝ $
C．{2,4, $ 5｝ $
D． $ ｛1,2,3｝ $
$ A\cup B=｛x\in \boldsymbol{N}|1\leqslant x\leqslant 6｝=｛1,2,3,4,5,6｝ $ ,集合 $ A=｛1,3,5,6｝ $ ,所以集合 $ B $ 中必有元素2,4,可能有元素1,3,5,6,只有选项 $ \mathrm{C} $ 符合.
3．已知集合 $ A=｛-1 {\rm ,0,1,2} $ , $ 3｝ $ ， $ B=｛x|\dfrac{x+1}{2}\in \boldsymbol{N}｝ $ ，则 $ A\cap B= $ （ ）
A． $ ｛0,1,2｝ $
B． $ ｛-1 {\rm ,1} $ , $ 3｝ $
C． $ ｛1,2｝ $
D． $ ｛1,3｝ $
因为集合 $ B=｛x|\dfrac{x+1}{2}\in \boldsymbol{N}｝=｛-1 {\rm ,1,3,5} $ , $ \cdots ｝ $ ， $ A=｛-1 {\rm ,0,1,2} $ , $ 3｝ $ ，所以 $ A\cap B=｛-1 {\rm ,1} $ , $ 3｝ $ .故选 $ \mathrm{B} $ .
4．已知集合 $ A=｛x|-6 < 2-x < -2｝ $ ， $ B=｛y|y=\dfrac{3}{4}x,x\in A｝ $ ，则 $ A\cap B= $ （ ）
A． $ ｛x|3 < x < 6｝ $
B． $ ｛x|4 < x < 6｝ $
C． $ ｛x|3 < x < 8｝ $
D． $ ｛x|4 < x < 8｝ $
由 $ -6 < 2-x < -2 $ 可得 $ 2 < x-2 < 6 $ ，所以 $ 4 < x < 8 $ ，所以 $ 3 < \dfrac{3}{4}x < 6 $ ，
所以 $ A=｛x|4 < x < 8｝ $ ， $ B=｛y|3 < y < 6｝ $ .
所以 $ A\cap B=｛x|4 < x < 6｝ $ .故选 $ \mathrm{B} $ .
5．设全集 $ U=\boldsymbol{R} $ ，集合 $ A=｛x|1 < x < 4｝ $ ， $ B=｛x|\dfrac{2}{x}\leqslant 1｝ $ ，则 $ A\cup ({\complement }_{U}B)= $ （ ）
A． $ ｛x|1 < x\leqslant 2｝ $
B． $ ｛x|1 < x < 2｝ $
C． $ ｛x|0 < x < 4｝ $
D． $ ｛x|0\leqslant x < 4｝ $
由 $ \dfrac{2}{x}\leqslant 1 $ ,解得 $ x < 0 $ 或 $ x\geqslant 2 $ ，即 $ B=｛x|x < 0 $ 或 $ x\geqslant 2｝ $ ，因此 $ {\complement }_{U}B=｛x|0\leqslant x < 2｝ $ .又 $ A=｛x|1 < x < 4｝ $ ，所以 $ A\cup ({\complement }_{U}B)=｛x|0\leqslant x < 4｝ $ .故选 $ \mathrm{D} $ .
6．已知集合 $ A=｛x|-2 < x < 1｝ $ ， $ B=｛x|x\leqslant 2｝ $ ，则集合 $ ｛x|x\leqslant -2 $ 或 $ x\geqslant 1｝= $ （ ）
A． $ A\cup B $
B． $ A\cap B $
C． $ {\complement }_{\boldsymbol{R}}(A\cup B) $
D． $ {\complement }_{\boldsymbol{R}}(A\cap B) $
因为 $ A=｛x|-2 < x < 1｝ $ , $ B=｛x|x\leqslant 2｝ $ ,所以 $ A\cup B=｛x|x\leqslant 2｝ $ , $ A\cap B=｛x|-2 < x < 1｝ $ ,所以 $ {\complement }_{\boldsymbol{R}}(A\cup B)=｛x|x > 2｝ $ , $ {\complement }_{\boldsymbol{R}}(A\cap B)=｛x|x\leqslant -2 $ 或 $ x\geqslant 1｝ $ .故选 $ \mathrm{D} $ .
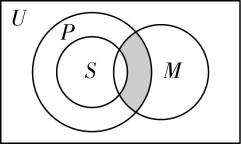
7．如图， $ U $ 为全集， $ M $ ， $ P $ ， $ S $ 是 $ U $ 的三个子集，则阴影部分所表示的集合是（ ）
A． $ (M\cap P)\cap S $
B． $ (M\cap P)\cup S $
C． $ (M\cap P)\cap ({\complement }_{U}S) $
D． $ (M\cap P)\cup ({\complement }_{U}S) $
在题图阴影部分所表示的集合中任取一个元素 $ x $ ，则 $ x\in M $ ， $ x\in P $ ， $ x\notin S $ ，所以阴影部分所表示的集合为 $ (M\cap P)\cap ({\complement }_{U}S). $ 故选 $ \mathrm{C} $ .
8．已知集合 $ A=｛2a-1 $ , $ {a}^{2} $ , $ 0｝ $ , $ B=｛1-a $ , $ a-5 $ , $ 9｝ $ ，若 $ A\cap B=｛9｝ $ ，则实数 $ a $ 的值为（ ）
A．5或 $ -3 $
B． $ ±3 $
C．5
D． $ -3 $
因为 $ A\cap B=｛9｝ $ ，所以 $ 9\in A $ ，所以 $ 2a-1=9 $ 或 $ {a}^{2}=9 $ .
若 $ 2a-1=9 $ ，则 $ a=5 $ ， $ A=｛9,25,0｝ $ , $ B=｛-4 {\rm ,0} $ , $ 9｝ $ ，此时 $ A\cap B=｛0,9｝ $ ,不符合题意；
若 $ {a}^{2}=9 $ ，则 $ a=3 $ 或 $ a=-3 $ ，
当 $ a=3 $ 时， $ 1-a=-2 $ , $ a-5=-2 $ ， $ B $ 中有两元素相等，故不符合题意；
当 $ a=-3 $ 时， $ A=｛-7 {\rm ,9} $ , $ 0｝ $ , $ B=｛4 $ , $ -8 $ , $ 9｝ $ ，此时 $ A\cap B=｛9｝ $ ，符合题意.
综上， $ a=-3 $ .故选 $ \mathrm{D} $ .
9．已知集合 $ A=｛x|(x-3)(x-a)=0 $ , $ a\in \boldsymbol{R}｝ $ ， $ B=｛x|(x-4)(x-1)=0｝ $ ，若 $ A\cap B=\mathrm{⌀} $ ， $ A\cup B=｛1,3,4｝ $ ，则实数 $ a $ 的值为（ ）
A．1
B． $ -3 $
C．4
D．3
集合 $ B=｛x|(x-4)(x-1)=0｝=｛1,4｝ $ ,易知 $ 3\in A $ , $ a\in A $ ,
$ \because A\cap B=\mathrm{⌀} $ , $ \therefore a\notin B $ .
$ \because A\cup B=｛1,3,4｝ $ , $ \therefore a=3 $ .故选 $ \mathrm{D} $ .
10．已知集合 $ M=｛x|x+m\geqslant 0｝ $ ， $ N=｛x|-2 < x < 4｝ $ ．若全集 $ U=\boldsymbol{R} $ ，且 $ ({\complement }_{U}M)\cap N=\mathrm{⌀} $ ，则实数 $ m $ 的取值范围是（ ）
A． $ ｛m|m < 2｝ $
B． $ ｛m|m\leqslant 2｝ $
C． $ ｛m|m\geqslant 2｝ $
D． $ ｛m|m\geqslant 2 $ 或 $ m\leqslant -4｝ $
因为 $ M=｛x|x+m\geqslant 0｝ $ , $ U=\boldsymbol{R} $ ,
所以 $ {\complement }_{U}M=｛x|x < -m｝ $ ,又 $ N=｛x|-2 < x < 4｝ $ ,
且 $ ({\complement }_{U}M)\cap N=\mathrm{⌀} $ ,所以 $ -m\leqslant -2 $ ,得 $ m\geqslant 2 $ ．故选 $ \mathrm{C} $ ．
11．已知 $ a\in \boldsymbol{R} $ ，集合 $ M=｛1 $ , $ {a}^{2}｝ $ , $ N=｛a $ , $ -1｝ $ .若 $ M\cup N $ 有三个元素，则 $ M\cap N= $ （ ）
A． $ ｛0,1｝ $
B． $ ｛0 $ , $ -1｝ $
C． $ ｛0｝ $
D． $ ｛1｝ $
因为集合 $ M=｛1 $ , $ {a}^{2}｝ $ , $ N=｛a $ , $ -1｝ $ , $ M\cup N $ 有三个元素,所以 $ {a}^{2}=a $ 且 $ a\ne ±1 $ ,解得 $ a=0 $ .此时 $ M\cap N=｛0｝ $ .故选 $ \mathrm{C} $ .
12．已知集合 $ A=｛x|x > 5｝ $ ， $ B=｛x|5a-1 < x < a+11｝ $ ，且 $ A\cup B=A $ ，则实数 $ a $ 的取值范围为（ ）
A． $ ｛a|a\leqslant -6｝ $
B． $ ｛a|a\geqslant \dfrac{6}{5}｝ $
C． $ ｛a|\dfrac{6}{5}\leqslant a < 3｝ $
D． $ ｛a|a\geqslant 3｝ $
因为 $ A\cup B=A $ ，所以 $ B\subseteq A $ .
若 $ B=\mathrm{⌀} $ ，则 $ 5a-1\geqslant a+11 $ ，即 $ a\geqslant 3 $ ；
若 $ B\ne \mathrm{⌀} $ ，则 $ \begin{cases}a < 3,\\ 5a-1\geqslant 5,\end{cases} $ 解得 $ \dfrac{6}{5}\leqslant a < 3 $ .综上，实数 $ a $ 的取值范围为 $ ｛a|a\geqslant \dfrac{6}{5}｝ $ .故选 $ \mathrm{B} $ .
1．已知全集 $ U=｛1,3,5,7,9,11｝ $ ，集合 $ A=｛3,5,7｝ $ ， $ B=｛3,7,9｝ $ ，则 $ ｛1,11｝= $ （ ）
A． $ A\cap B $
B． $ A\cup B $
C． $ {\complement }_{U}(A\cap B) $
D． $ {\complement }_{U}(A\cup B) $
由于 $ A\cap B=｛3,7｝ $ , $ A\cup B=｛3,5,7,9｝ $ ，从而 $ {\complement }_{U}(A\cap B)=｛1,5,9,11｝ $ , $ {\complement }_{U}(A\cup B)=｛1,11｝ $ ．故选 $ \mathrm{D} $ ．
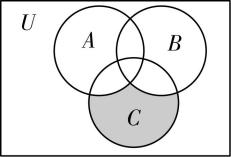
2．如图所示， $ U $ 为全集， $ A $ ， $ B $ ， $ C $ 为 $ U $ 的子集，则阴影部分所表示的集合可以为（ ）
A． $ (A\cup B)\cap C $
B． $ ({\complement }_{U}A)\cup (B\cap C) $
C． $ ({\complement }_{U}A)\cap (B\cup C) $
D． $ ({\complement }_{U}(A\cup B))\cap C $
由题图可知，阴影部分所表示的集合为集合 $ A $ 与集合 $ B $ 的并集在全集 $ U $ 中的补集再与集合 $ C $ 的交集，用符号表示为 $ ({\complement }_{U}(A\cup B))\cap C $ ，即 $ \mathrm{D} $ 符合，其他选项的表示不符合.故选 $ \mathrm{D} $ .
3．已知集合 $ A=｛x\left|\mathrm{ }\right|x-1| > 2｝ $ ，集合 $ B=｛x|mx+1 < 0｝ $ ，若 $ A\cup B=A $ ，则实数 $ m $ 的取值范围是（ ）
A． $ ｛m|-\dfrac{1}{3}\leqslant m\leqslant 0｝ $
B． $ ｛m|-\dfrac{1}{3}\leqslant m\leqslant 1｝ $
C． $ ｛m|0\leqslant m\leqslant 1｝ $
D． $ ｛m|-\dfrac{1}{3}\leqslant m < 0或0 < m\leqslant 1｝ $
因为 $ \left|x-1\right| > 2 $ ,所以 $ x-1 > 2 $ 或 $ x-1 < -2 $ ,解得 $ x > 3 $ 或 $ x < -1 $ ,
即 $ A=｛x|x > 3 $ 或 $ x < -1｝ $ .
因为 $ A\cup B=A $ ,所以 $ B\subseteq A $ .当 $ m=0 $ 时, $ B=\mathrm{⌀} $ ,满足要求.
当 $ m > 0 $ 时, $ mx+1 < 0⇒x < -\dfrac{1}{m}. $ ,由 $ B\subseteq A $ ,
可得 $ -\dfrac{1}{m}\leqslant -1⇒m\leqslant 1. $ ,即 $ 0 < m\leqslant 1 $ .
当 $ m < 0 $ 时, $ mx+1 < 0⇒x > -\dfrac{1}{m}. $ ,由 $ B\subseteq A $ ,
可得 $ -\dfrac{1}{m}\geqslant 3⇒m\geqslant -\dfrac{1}{3}. $ ,即 $ -\dfrac{1}{3}\leqslant m < 0 $ .
综上所述, $ -\dfrac{1}{3}\leqslant m\leqslant 1 $ .故选B.
4．已知全集为 $ U $ ，集合 $ M $ ， $ \mathbf{N} $ 满足 $ M\subseteq N\subseteq U $ ，则下列运算结果一定为 $ U $ 的是（ ）
A． $ M\cup N $
B． $ ({\complement }_{U}N)\cup ({\complement }_{U}M) $
C． $ M\cup ({\complement }_{U}N) $
D． $ N\cup ({\complement }_{U}M) $
由 $ M\subseteq N\subseteq U $ 得当 $ N⫋U $ 时, $ M\cup N=N⫋U $ ,故选项 $ \mathrm{A} $ 不正确；
$ ({\complement }_{U}N)\cup ({\complement }_{U}M)={\complement }_{U}(M\cap N)={\complement }_{U}M $ ,当 $ M\ne \mathrm{⌀} $ 时, $ {\complement }_{U}M⫋U $ ,故选项 $ \mathrm{B} $ 不正确；
当 $ M⫋N $ 时, $ M\cup ({\complement }_{U}N)⫋U $ ,故选项 $ \mathrm{C} $ 不正确；
因为 $ M\subseteq N\subseteq U $ ,所以 $ N\cup ({\complement }_{U}M)=U $ ,故选项 $ \mathrm{D} $ 正确.
故选 $ \mathrm{D} $ .
5．已知集合 $ A=｛{x}^{2}+8|x\in \boldsymbol{N}｝ $ , $ B=｛{y}^{2}+17|y\in \boldsymbol{N}｝ $ .若 $ A\cap B=C $ ，则集合 $ C $ 中的元素个数为（ ）
A．0
B．1
C．2
D．3
由 $ A\cap B=C $ 可得集合 $ C $ 为集合 $ A $ ， $ B $ 的公共元素，需满足 $ {x}^{2}+8={y}^{2}+17 $ ，即 $ {x}^{2}-{y}^{2}=9 $ ，即 $ (x+y)\cdot (x-y)=9 $ ，又 $ x $ , $ y\in \boldsymbol{N} $ ，所以 $ \begin{cases}x+y=9,\\ x-y=1\end{cases} $ 或 $ \begin{cases}x+y=3,\\ x-y=3,\end{cases} $
解得 $ \begin{cases}x=5,\\ y=4\end{cases} $ 或 $ \begin{cases}x=3,\\ y=0.\end{cases} $ 此时集合 $ C=｛17,33｝ $ 有2个元素.故选 $ \mathrm{C} $ .
6．某校举行“语文情境默写”“英语读后续写”两项竞赛，某班派出20人参赛，据了解其中擅长语文的有10名同学，擅长英语的有12名同学，两项都擅长的有5名同学，则20人中两项均不擅长的同学的人数为（ ）
A．1
B．2
C．3
D．5
设这20名同学构成全集 $ U $ ，其中擅长语文的同学构成集合 $ A $ ，擅长英语的同学构成集合 $ B $ ，
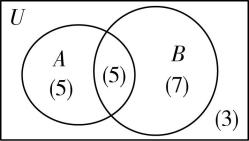
则 $ \mathrm{c}\mathrm{a}\mathrm{r}\mathrm{d}(U)=20 $ ， $ \mathrm{c}\mathrm{a}\mathrm{r}\mathrm{d}(A)=10 $ ， $ \mathrm{c}\mathrm{a}\mathrm{r}\mathrm{d}(B)=12 $ ， $ \mathrm{c}\mathrm{a}\mathrm{r}\mathrm{d}(A\cap B)=5 $ ，
$ \therefore \mathrm{c}\mathrm{a}\mathrm{r}\mathrm{d}(A\cup B)=\mathrm{c}\mathrm{a}\mathrm{r}\mathrm{d}(A)+\mathrm{c}\mathrm{a}\mathrm{r}\mathrm{d}(B)-\mathrm{c}\mathrm{a}\mathrm{r}\mathrm{d}(A\cap B)=10+12-5=17 $ ， $ \therefore \mathrm{c}\mathrm{a}\mathrm{r}\mathrm{d}({\complement }_{U}(A\cup B))=20-17=3 $ ，
$ \therefore $ 语文和英语均不擅长的同学的人数为3．故选 $ \mathrm{C} $ ．
7．（多选）定义集合运算 $ M-N=｛x|x\in M $ 且 $ x\notin \mathbf{N}｝ $ ，称为集合 $ M $ 与集合 $ \mathbf{N} $ 的差集；定义集合运算 $ M\mathrm{\Delta }N=(M-N)\cup (N-M) $ ,称为集合 $ M $ 与集合 $ \mathbf{N} $ 的对称差.有以下四个等式,其中正确的是（ ）（多选）
A． $ M\mathrm{\Delta }N=N\mathrm{\Delta }M $
B． $ (M\mathrm{\Delta }N)\mathrm{\Delta }P=M\mathrm{\Delta }(N\mathrm{\Delta }P) $
C． $ M\cap (N\mathrm{\Delta }P)=(M\cap N)\mathrm{\Delta }(M\cap P) $
D． $ M\cup (N\mathrm{\Delta }P)=(M\cup N)\mathrm{\Delta }(M\cup P) $
$ \mathrm{A} $ 选项,假设全集为 $ U $ ，由题意得 $ M-N=M\cap ({\complement }_{U}N) $ , $ N-M=N\cap ({\complement }_{U}M) $ ,所以 $ M\mathrm{\Delta }N=(M\cap ({\complement }_{U}N))\cup (N\cap ({\complement }_{U}M)) $ , $ N\mathrm{\Delta }M=(N\cap ({\complement }_{U}M))\cup (M\cap ({\complement }_{U}N)) $ ,所以 $ M\mathrm{\Delta }N=N\mathrm{\Delta }M $ , $ \mathrm{A} $ 正确.
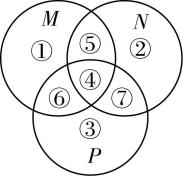
由题意, $ M\mathrm{\Delta }N $ 表示的运算为集合 $ M $ 与 $ \mathbf{N} $ 的并集中去掉 $ M $ 与 $ \mathbf{N} $ 的交集部分,
不妨设 $ M $ , $ \mathbf{N} $ , $ P $ 均有交集,如图所示.
$ \mathrm{B} $ 选项, $ M\mathrm{\Delta }N $ 表示①②⑥⑦部分的并集, $ (M\mathrm{\Delta }N)\mathrm{\Delta }P $ 表示①②⑥⑦与③④⑥⑦的并集去掉两者的交集,
即 $ (M\mathrm{\Delta }N)\mathrm{\Delta }P $ 表示①②③④部分的并集,
$ \mathbf{N}\mathrm{\Delta }P $ 表示②③⑤⑥部分的并集, $ M\mathrm{\Delta }(N\mathrm{\Delta }P) $ 表示②③⑤⑥与①④⑤⑥的并集去掉两者的交集,
即 $ M\mathrm{\Delta }(N\mathrm{\Delta }P) $ 表示①②③④部分的并集,故 $ (M\mathrm{\Delta }N)\mathrm{\Delta }P=M\mathrm{\Delta }(N\mathrm{\Delta }P) $ , $ \mathrm{B} $ 正确.
$ \mathrm{C} $ 选项,通过推理知 $ M\cap (N\mathrm{\Delta }P) $ , $ (M\cap N)\mathrm{\Delta } $
$ (M\cap P) $ 均表示⑤⑥部分的并集, $ \mathrm{C} $ 正确.
$ \mathrm{D} $ 选项,通过推理得到 $ M\cup (N\mathrm{\Delta }P) $ 表示①②③④⑤⑥部分的并集,
$ M\cup N $ 表示①②④⑤⑥⑦部分的并集, $ M\cup P $ 表示①③④⑤⑥⑦部分的并集,
$ (M\cup N)\mathrm{\Delta }(M\cup P) $ 表示①②④⑤⑥⑦与①③④⑤⑥⑦的并集去掉两者的交集,
即②③部分的并集, $ \mathrm{D} $ 错误.
故选 $ \mathrm{A}\mathrm{B}\mathrm{C} $ .
8．已知集合 $ A=｛x|0 < x < 3｝ $ ， $ B=｛x|a-3 < x < 2a-1｝ $ ．
（1） 若 $ a=4 $ ，求 $ ({\complement }_{\boldsymbol{R}}A)\cup B $ ；
（2） 若 $ A\cup B=B $ ，求实数 $ a $ 的取值范围．
（1） 【解】由 $ a=4 $ 得， $ B=｛x|1 < x < 7｝ $ ，
因为 $ A=｛x|0 < x < 3｝ $ ， $ {\complement }_{\boldsymbol{R}}A=｛x|x\leqslant 0 $ 或 $ x\geqslant 3｝ $ ，
所以 $ ({\complement }_{\boldsymbol{R}}A)\cup B=｛x|x\leqslant 0 $ 或 $ x > 1｝ $ ．
（2） 因为 $ A\cup B=B $ ，所以 $ A\subseteq B $ ．
由于 $ A=｛x|0 < x < 3｝ $ ，故 $ B\ne \mathrm{⌀} $ ，
可得 $ \begin{cases}2a-1 > a-3,\\ a-3\leqslant 0,\\ 2a-1\geqslant 3\end{cases}⇒\begin{cases}a > -2,\\ a\leqslant 3,\\ a\geqslant 2,\end{cases} $ 故 $ 2\leqslant a\leqslant 3 $ ．
综上可知，实数 $ a $ 的取值范围为 $ ｛a|2\leqslant a\leqslant 3｝ $ ．
9．全集 $ U $ 有2 024个元素，若 $ |A|=2000 $ ， $ |B|=1978 $ ， $ |C|=1958 $ ，且 $ U=A\cup B\cup C $ ，则 $ |A\cap B\cap C{|}_{ \min }= $ .
注： $ |A| $ 表示集合 $ A $ 中的元素个数.
1 888
$ |A\cap B|=|A|+|B|-|A\cup B|\geqslant 2000+1978-2024=1954 $ ，
$ |A\cap C|=|A|+|C|-|A\cup C|\geqslant 2000+1958-2024=1934 $ ，
$ |B\cap C|=|B|+|C|-|B\cup C|\geqslant 1978+1958-2024=1912 $ .
由 $ U=A\cup B\cup C $ 及集合的容斥原理有 $ |A\cap B\cap C|=|U|-|A|-|B|-|C|+|A\cap B|+|A\cap C|+|B\cap C|\geqslant 1888 $ ，
等号可在 $ A\cup B=A\cup C=B\cup C=U $ 时取得.
10．设集合 $ A=｛(x,y)|x+y=1｝ $ , $ B=｛(x,y)|{x}^{2}+{y}^{2}=2｝ $ , $ C=A\cap B $ ,则集合 $ C $ 的子集的个数是 ．
4
联立 $ \begin{cases}x+y=1,\\ {x}^{2}+{y}^{2}=2,\end{cases} $ 消去 $ y $ 得 $ 2{x}^{2}-2x-1=0 $ , $ \mathrm{\Delta }=(-2)^{2}+4×2×1 > 0 $ ,可知方程有两个不同的解，故集合 $ C $ 中有2个元素，故 $ C $ 的子集有 $ {2}^{2}=4 $ 个．