6.定义差集 $ A-B={x|x\in A $ ,且 $ x\notin B} $ ,现有三个集合 $ A $ , $ B $ , $ C $ 分别用圆表示,则集合 $ C-(A-B) $ 用阴影部分表示正确的为( )
A.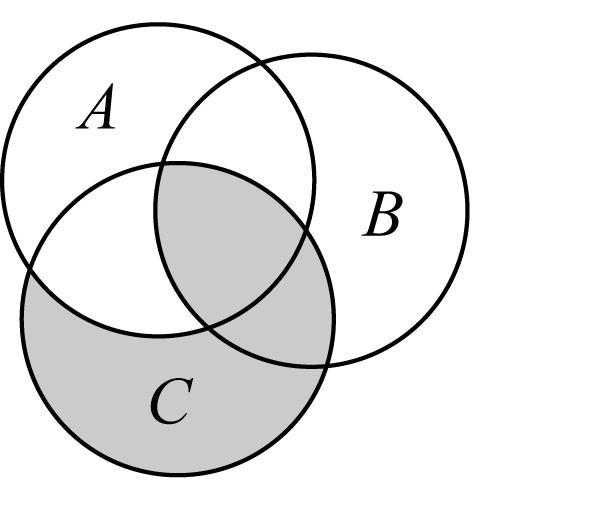
B.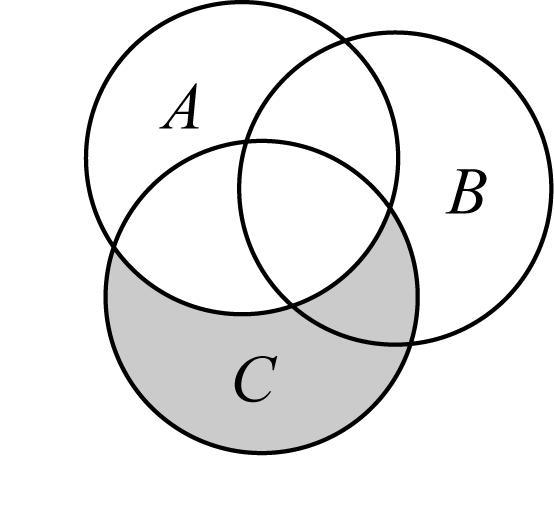
C.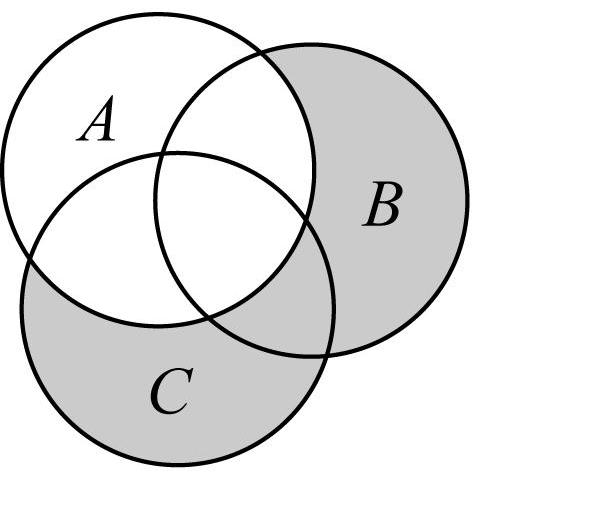
D.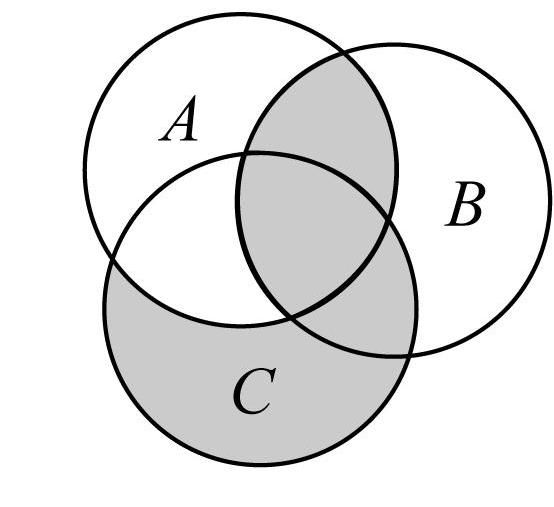
如图所示, $ A-B $ 表示图中阴影部分,故集合 $ C-(A-B) $ 所含元素属于 $ C $ ,但不属于图中阴影部分,故选 $ \mathrm{A} $ .
1.已知集合 $ A={x|-2\leqslant x\leqslant 10} $ , $ B={x|1-m\leqslant x\leqslant 1+m} $ .若 $ \mathrm{B}\cap ({\complement }_{\boldsymbol{R}}A)=\mathrm{⌀} $ ,则实数 $ m $ 的取值范围为( )
A. $ {m|m\leqslant 3} $
B. $ {m|m\leqslant 9} $
C. $ {m|m\leqslant 3 $ 或 $ m\geqslant 9} $
D. $ {m|3\leqslant m\leqslant 9} $
$ {\complement }_{\boldsymbol{R}}A={x|x < -2 $ 或 $ x > 10} $ .因为 $ B\cap ({\complement }_{\boldsymbol{R}}A)=\mathrm{⌀} $ ,所以 $ B\subseteq A $ .已知 $ B={x|1-m\leqslant x\leqslant 1+m} $ ,要满足 $ B\subseteq A $ ,
则当 $ B=\mathrm{⌀} $ 时, $ 1-m > 1+m $ ,解得 $ m < 0 $ .
当 $ B\ne \mathrm{⌀} $ 时,有 $ \begin{cases}m\geqslant 0,\\ 1-m\geqslant -2,\\ 1+m\leqslant 10,\end{cases} $ 解得 $ 0\leqslant m\leqslant 3 $ .
综上,实数 $ m $ 的取值范围为 $ {m|m\leqslant 3} $ .故选 $ \mathrm{A} $ .
2.已知集合 $ A={x|1\leqslant x\leqslant 5} $ , $ B={x|ax-1\geqslant 0} $ .
(1) 若 $ a=\dfrac{1}{2} $ ,求 $ A\cap ({\complement }_{\boldsymbol{R}}B) $ .
(2) 从 $ \mathrm{①}A\cap B=A $ ; $ \mathrm{②}B\cup ({\complement }_{\boldsymbol{R}}A)=\boldsymbol{R} $ ; $ \mathrm{③}A\cap ({\complement }_{\boldsymbol{R}}B)=\mathrm{⌀} $ 这三个条件中任选一个,补充在下面的横线上,并进行解答.
问题:若 ,求实数 $ a $ 的取值范围.
注:若选择多个条件分别解答,则按第一个解答计分.
(1) 【解】当 $ a=\dfrac{1}{2} $ 时, $ B={x|\dfrac{1}{2}x-1\geqslant 0}={x|x\geqslant 2} $ ,则 $ {\complement }_{\boldsymbol{R}}B={x|x < 2} $ ,则 $ A\cap ({\complement }_{\boldsymbol{R}}B)={x|1\leqslant x < 2} $ .
(2) 【解】若选①, $ A\cap B=A $ ,可得 $ A\subseteq B $ ,则 $ B\ne \mathrm{⌀} $ ,即 $ a\ne 0 $ .
当 $ a < 0 $ 时, $ B={x|x\leqslant \dfrac{1}{a}} $ ,由 $ {x|1\leqslant x\leqslant 5}\subseteq {x|x\leqslant \dfrac{1}{a}} $ ,可得 $ \dfrac{1}{a}\geqslant 5 $ ,此时无解;
当 $ a > 0 $ 时, $ B={x|x\geqslant \dfrac{1}{a}} $ ,由 $ {x|1\leqslant x\leqslant 5}\subseteq {x|x\geqslant \dfrac{1}{a}} $ ,可得 $ \dfrac{1}{a}\leqslant 1 $ ,解得 $ a\geqslant 1 $ .
综上,实数 $ a $ 的取值范围为 $ {a|a\geqslant 1} $ .
若选②,因为 $ {\complement }_{\boldsymbol{R}}A={x|x < 1 $ 或 $ x > 5} $ ,又 $ B\cup ({\complement }_{\boldsymbol{R}}A)=\boldsymbol{R} $ ,则 $ B\ne \mathrm{⌀} $ ,即 $ a\ne 0 $ .
当 $ a < 0 $ 时, $ B={x|x\leqslant \dfrac{1}{a}} $ ,需使 $ \dfrac{1}{a}\geqslant 5 $ ,此时无解;
当 $ a > 0 $ 时, $ B={x|x\geqslant \dfrac{1}{a}} $ ,需使 $ \dfrac{1}{a}\leqslant 1 $ ,解得 $ a\geqslant 1 $ .
综上,实数 $ a $ 的取值范围为 $ {a|a\geqslant 1} $ .
若选③,因为 $ A\cap ({\complement }_{\boldsymbol{R}}B)=\mathrm{⌀} $ ,所以 $ A\subseteq B $ ,则 $ B\ne \mathrm{⌀} $ ,即 $ a\ne 0 $ .
当 $ a < 0 $ 时, $ B={x|x\leqslant \dfrac{1}{a}} $ ,需使 $ \dfrac{1}{a}\geqslant 5 $ ,此时无解;
当 $ a > 0 $ 时, $ B={x|x\geqslant \dfrac{1}{a}} $ ,需使 $ \dfrac{1}{a}\leqslant 1 $ ,解得 $ a\geqslant 1 $ .
综上,实数 $ a $ 的取值范围为 $ {a|a\geqslant 1} $ .
3.已知集合 $ M={x|-3 < x\leqslant 2} $ , $ N={x|0 < x < 2} $ ,全集 $ U={x|-6\leqslant x\leqslant 5} $ .
(1) 求 $ N\cup ({\complement }_{U}M) $ ;
(2) 若 $ C={x|a\leqslant x\leqslant 2a-1} $ ,且 $ C\subseteq {\complement }_{U}M $ ,求实数 $ a $ 的取值范围.
(1) 【解】因为 $ U={x|-6\leqslant x\leqslant 5} $ , $ M={x|-3 < x\leqslant 2} $ ,所以 $ {\complement }_{U}M={x|-6\leqslant x\leqslant -3 $ 或 $ 2 < x\leqslant 5} $ ,
又因为 $ N={x|0 < x < 2} $ ,所以 $ N\cup ({\complement }_{U}M)={x|-6\leqslant x\leqslant -3 $ 或 $ 0 < x < 2 $ 或 $ 2 < x\leqslant 5} $ .
(2) 【解】由(1)可知 $ {\complement }_{U}M={x|-6\leqslant x\leqslant -3 $ 或 $ 2 < x\leqslant 5} $ ,
当 $ C=\mathrm{⌀} $ 时, $ C\subseteq {\complement }_{U}M $ 成立,此时 $ a > 2a-1 $ ,解得 $ a < 1 $ ;
当 $ C\ne \mathrm{⌀} $ 时,因为 $ C\subseteq {\complement }_{U}M $ ,
所以 $ \begin{cases}a\leqslant 2a-1,\\ 2a-1\leqslant -3,\\ a\geqslant -6\end{cases} $ 或 $ \begin{cases}a\leqslant 2a-1,\\ 2a-1\leqslant 5,\\ a > 2,\end{cases} $
解得 $ 2 < a\leqslant 3 $ .
故实数 $ a $ 的取值范围是 $ {a|a < 1 $ 或 $ 2 < a\leqslant 3} $ .
4.对于任意两个正整数 $ m $ , $ n $ ,定义某种运算“ $ \mathrm{※} $ ”如下:当 $ m $ , $ n $ 都为正偶数或都为正奇数时, $ m\mathrm{※}n=m+n $ ;当 $ m $ , $ n $ 中一个为正偶数,另一个为正奇数时, $ m\mathrm{※}n=mn $ .在此定义下,集合 $ M={(m,n)|m\mathrm{※}n=8} $ 中的元素个数是( )
A.10
B.9
C.8
D.7
①当 $ m $ , $ n $ 都为正偶数时,符合条件的 $ (m,n) $ 有 $ (2,6) $ , $ (4,4) $ , $ (6,2) $ ,共3个;
②当 $ m $ , $ n $ 都为正奇数时,符合条件的 $ (m,n) $ 有 $ (1,7) $ , $ (3,5) $ , $ (5,3) $ , $ (7,1) $ ,共4个;
③当 $ m $ , $ n $ 中一个为正偶数,一个为正奇数时,符合条件的 $ (m,n) $ 有 $ (1,8) $ , $ (8,1) $ ,共2个.所以集合 $ M $ 的元素个数是 $ 3+4+2=9 $ .故选 $ \mathrm{B} $ .
5.(多选)大数据时代,需要对数据库进行检索,检索过程中有时会出现笛卡尔积现象,而笛卡尔积会产生大量的数据,对内存、计算资源都会产生巨大压力,为优化检索软件,编程人员需要了解笛卡尔积.已知两个集合 $ A $ 和 $ B $ ,用 $ A $ 中元素为第一元素, $ B $ 中元素为第二元素构成有序对,所有这样的有序对组成的集合叫作 $ A $ 与 $ B $ 的笛卡尔积,又称直积,记为 $ A×B $ ,即 $ A×B={(x,y)|x\in A $ 且 $ y\in B} $ .关于任意非空集合 $ M $ , $ \mathbf{N} $ , $ T $ ,下列说法错误的是( )(多选)
A. $ M×N=N×M $
B. $ (M×N)×T=M×(N×T) $
C. $ M×(N\cup T)\ne (M×N)\cup (M×T) $
D. $ M×(N\cap T)=(M×N)\cap (M×T) $
对于 $ \mathrm{A} $ ,若 $ M={1} $ , $ N={1,2} $ ,则 $ M×N={(1,1) $ , $ (1,2)} $ , $ N×M={(1,1) $ , $ (2,1)} $ ,所以 $ M×N\ne N×M $ ,故 $ \mathrm{A} $ 错误;
对于 $ \mathrm{B} $ ,若 $ M={1} $ , $ N={2} $ , $ T={3} $ ,
则 $ M×N={(1,2)} $ , $ (M×N)×T={((1,2),3)} $ ,而 $ M×(N×T)={(1,(2,3))} $ ,所以 $ (M×N)×T\ne M×(N×T) $ ,故 $ \mathrm{B} $ 错误;
对于 $ \mathrm{C} $ ,若 $ M={1} $ , $ N={2} $ , $ T={3} $ ,则 $ M×(N\cup T)={(1,2) $ , $ (1,3)} $ ,
$ M×N={(1,2)} $ , $ M×T={(1,3)} $ ,所以 $ M×(N\cup T)=(M×N)\cup (M×T) $ ,故 $ \mathrm{C} $ 错误;
对于 $ \mathrm{D} $ ,任取元素 $ (x,y)\in M×(N\cap T) $ ,则 $ x\in M $ 且 $ y\in \mathbf{N}\cap T $ ,则 $ y\in \mathbf{N} $ 且 $ y\in T $ ,
于是 $ (x,y)\in M×N $ 且 $ (x,y)\in M×T $ ,即 $ (x,y)\in (M×N)\cap (M×T) $ ,
反之若任取元素 $ (x,y)\in (M×N)\cap (M×T) $ ,
则 $ (x,y)\in M×N $ 且 $ (x,y)\in M×T $ ,
因此 $ x\in M $ , $ y\in \mathbf{N} $ 且 $ y\in T $ ,即 $ x\in M $ 且 $ y\in \mathbf{N}\cap T $ ,
所以 $ (x,y)\in M×(N\cap T) $ ,即 $ M×(N\cap T)=(M×N)\cap (M×T) $ ,故 $ \mathrm{D} $ 正确.故选 $ \mathrm{A}\mathrm{B}\mathrm{C} $ .
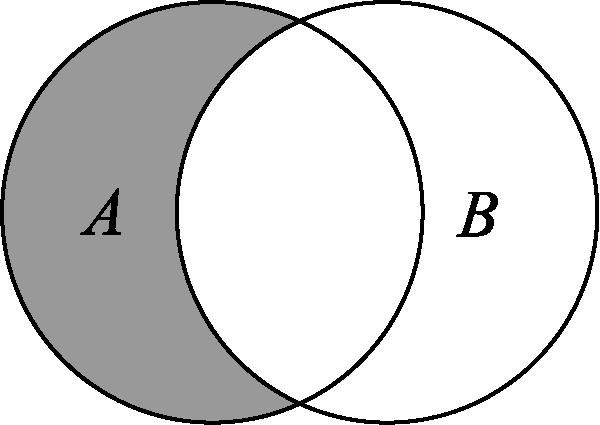
6.定义差集 $ A-B={x|x\in A $ ,且 $ x\notin B} $ ,现有三个集合 $ A $ , $ B $ , $ C $ 分别用圆表示,则集合 $ C-(A-B) $ 用阴影部分表示正确的为( )
A.
B.
C.
D.
如图所示, $ A-B $ 表示图中阴影部分,故集合 $ C-(A-B) $ 所含元素属于 $ C $ ,但不属于图中阴影部分,故选 $ \mathrm{A} $ .

7.某年级先后举办了数学、历史、化学讲座,其中有70人听了数学讲座,62人听了历史讲座,58人听了化学讲座,记 $ A={x|x $ 是听了数学讲座的学生 $ } $ , $ B={x|x $ 是听了历史讲座的学生 $ } $ , $ C={x|x $ 是听了化学讲座的学生}.用 $ \mathrm{c}\mathrm{a}\mathrm{r}\mathrm{d}(M) $ 来表示有限集合 $ M $ 中元素的个数,若 $ \mathrm{c}\mathrm{a}\mathrm{r}\mathrm{d}(A\cap B)=17 $ , $ \mathrm{c}\mathrm{a}\mathrm{r}\mathrm{d}(A\cap C)=13 $ , $ \mathrm{c}\mathrm{a}\mathrm{r}\mathrm{d}(B\cap C)=5 $ , $ A\cap B\cap C=\mathrm{⌀} $ ,则( )
A. $ \mathrm{c}\mathrm{a}\mathrm{r}\mathrm{d}(A\cap B\cap C)=35 $
B. $ \mathrm{c}\mathrm{a}\mathrm{r}\mathrm{d}(A\cup B)=115 $
C. $ \mathrm{c}\mathrm{a}\mathrm{r}\mathrm{d}(B\cup C)=120 $
D. $ \mathrm{c}\mathrm{a}\mathrm{r}\mathrm{d}(A\cup B\cup C)=190 $
$ \mathrm{A} $ 选项,由已知 $ A\cap B\cap C=\mathrm{⌀} $ ,得 $ \mathrm{c}\mathrm{a}\mathrm{r}\mathrm{d}(A\cap B\cap C)=0 $ , $ \mathrm{A} $ 错误;
$ \mathrm{B} $ 选项, $ \mathrm{c}\mathrm{a}\mathrm{r}\mathrm{d}(A\cup B)=\mathrm{c}\mathrm{a}\mathrm{r}\mathrm{d}(A)+\mathrm{c}\mathrm{a}\mathrm{r}\mathrm{d}(B)-\mathrm{c}\mathrm{a}\mathrm{r}\mathrm{d}(A\cap B)=70+62-17=115 $ , $ \mathrm{B} $ 正确;
$ \mathrm{C} $ 选项, $ \mathrm{c}\mathrm{a}\mathrm{r}\mathrm{d}(B\cup C)=\mathrm{c}\mathrm{a}\mathrm{r}\mathrm{d}(B)+\mathrm{c}\mathrm{a}\mathrm{r}\mathrm{d}(C)-\mathrm{c}\mathrm{a}\mathrm{r}\mathrm{d}(B\cap C)=62+58-5=115 $ , $ \mathrm{C} $ 错误;
$ \mathrm{D} $ 选项, $ \mathrm{c}\mathrm{a}\mathrm{r}\mathrm{d}(A\cup B\cup C)=\mathrm{c}\mathrm{a}\mathrm{r}\mathrm{d}(A)+\mathrm{c}\mathrm{a}\mathrm{r}\mathrm{d}(B)+\mathrm{c}\mathrm{a}\mathrm{r}\mathrm{d}(C)-\mathrm{c}\mathrm{a}\mathrm{r}\mathrm{d}(A\cap B)-\mathrm{c}\mathrm{a}\mathrm{r}\mathrm{d}(A\cap C)-\mathrm{c}\mathrm{a}\mathrm{r}\mathrm{d}(B\cap C)+\mathrm{c}\mathrm{a}\mathrm{r}\mathrm{d}(A\cap B\cap C)=70+62+58-17-13-5+0=155 $ , $ \mathrm{D} $ 错误.故选 $ \mathrm{B} $ .
8.已知集合 $ A={x|{x}^{2}+2024x+2025=0} $ , $ B={x|({x}^{2}+ax)({x}^{2}+4ax+4)=0} $ ,记非空集合 $ S $ 的元素个数为 $ n(S) $ ,已知 $ |n(A)-n(B)|=1 $ ,记实数 $ a $ 的所有可能取值构成的集合为 $ M $ ,则 $ M $ 的非空子集的个数是 .
31
对于 $ {x}^{2}+2024x+2025=0 $ ,有 $ \mathrm{\Delta }={2024}^{2}-4×2025 > 0 $ ,
所以集合 $ A={x|{x}^{2}+2024x+2025=0} $ 中有两个元素,即 $ n(A)=2 $ .
因为 $ |n(A)-n(B)|=1 $ ,所以 $ n(B)=1 $ 或3.
对于 $ ({x}^{2}+ax)({x}^{2}+4ax+4)=0 $ ,易知 $ x=0 $ 必是方程的一个解.
当 $ n(B)=1 $ 时, $ B={0} $ ,所以 $ {x}^{2}+ax=0 $ 有两个相等的实数根,且 $ {x}^{2}+4ax+4=0 $ 无解,
则 $ \begin{cases}{\mathrm{\Delta }}_{1}={a}^{2}-4×0=0,\\ {\mathrm{\Delta }}_{2}={\left(4a\right) ^ {2}}-4×4 < 0,\end{cases} $ 解得 $ a=0 $ .
当 $ n(B)=3 $ 时,若 $ {x}^{2}+ax=0 $ 有两个相等的实数根,由上述分析可知 $ {x}^{2}+4ax+4=0 $ 无解,不满足题意.
若 $ {x}^{2}+ax=0 $ 有两个不相等的实数根,即 $ {x}_{1}=0 $ , $ {x}_{2}=-a $ ,则
$ \mathrm{①}{x}^{2}+4ax+4=0 $ 有两个相等且异于方程 $ {x}^{2}+ax=0 $ 的根,则 $ \begin{cases}{\mathrm{\Delta }}_{1}={a}^{2}-4×0 > 0,\\ {\mathrm{\Delta }}_{2}={\left(4a\right) ^ {2}}-4×4=0,\end{cases} $ 解得 $ a=-1 $ 或1,经检验均满足题意;
$ \mathrm{②}{x}^{2}+4ax+4=0 $ 有两个不等的实数根,且其中一根也是 $ {x}^{2}+ax=0 $ 的根,则 $ x=-a $ 是方程 $ {x}^{2}+4ax+4=0 $ 的根,代入得 $ a=±\dfrac{2\sqrt{3}}{3} $ ,此时方程 $ {x}^{2}±\dfrac{8\sqrt{3}}{3}x+4=0 $ 的判别式 $ {\mathrm{\Delta }}_{2} > 0 $ ,方程 $ {x}^{2}+ax=0 $ 的判别式 $ {\mathrm{\Delta }}_{1} > 0 $ ,满足题意.
综上,实数 $ a $ 的所有可能取值为 $ -\dfrac{2\sqrt{3}}{3} $ , $ -1 {\rm ,0,1} $ , $ \dfrac{2\sqrt{3}}{3} $ ,则 $ M={-\dfrac{2\sqrt{3}}{3},-1,0,1,\dfrac{2\sqrt{3}}{3}} $ ,
经检验,均符合题意.
所以 $ M $ 的非空子集的个数为 $ {2}^{5}-1=31 $ .
9.已知集合 $ A={(x,y)|mx+y=-1} $ , $ B={(x,y)|2x+ny=7} $ ,甲、乙两名同学在进行 $ A\cap B $ 的运算时,甲看错了 $ m $ ,解得 $ A\cap B={(2,3)} $ ;乙看错了 $ n $ ,解得 $ A\cap B={(3,2)} $ .
(1) 求实数 $ m $ , $ n $ 的值;
(2) 求集合 $ A\cap B $ .
(1) 【解】将 $ (2,3) $ 代入 $ 2x+ny=7 $ ,得 $ 4+3n=7 $ ,解得 $ n=1 $ .
将 $ (3,2) $ 代入 $ mx+y=-1 $ ,得 $ 3m+2=-1 $ ,解得 $ m=-1 $ ,所以 $ m=-1 $ , $ n=1 $ .
(2) 【解】由(1)知 $ \begin{cases}-x+y=-1,\\ 2x+y=7,\end{cases} $ 解得 $ \begin{cases}x=\dfrac{8}{3},\\ y=\dfrac{5}{3},\end{cases} $
所以 $ A\cap B={(\dfrac{8}{3},\dfrac{5}{3})} $ .
10.已知集合 $ A $ , $ B $ , $ A\subseteq \mathrm{Z} $ , $ B\subseteq \mathrm{Z} $ , $ A $ , $ B $ 中都至少有3个元素,且 $ A $ , $ B $ 满足:
$ \mathrm{①}\forall x $ , $ y\in A $ ,且 $ x\ne y $ ,总有 $ |x+y|\in B $ ;
$ \mathrm{②}\forall x $ , $ y\in B $ ,且 $ x\ne y $ ,总有 $ |x-y|\in A $ .
(1) 若集合 $ B={1,2,3} $ ,直接写出所有满足条件的集合 $ A $ .
(2) 已知 $ -1\in A $ ,
(ⅰ) 若 $ x $ , $ y\in A $ ,且 $ y > x > 0 $ ,求证: $ y-x\in A $ .
(ⅱ) 求证: $ {\mathrm{N}}^{\ast }\subseteq A $ .
(1) 【解】因为 $ B={1,2,3} $ ,又 $ \forall x $ , $ y\in B $ ,且 $ x\ne y $ ,总有 $ |x-y|\in A $ ,
所以 $ 3-1\in A $ , $ 3-2\in A $ ,即 $ 1\in A $ , $ 2\in A $ .
设 $ t\in A $ , $ t\ne 1 $ , $ t\ne 2 $ ,由 $ \forall x $ , $ y\in A $ ,且 $ x\ne y $ ,总有 $ |x+y|\in B $ ,
可得 $ |t+1|\in B $ ,且 $ |t+2|\in B $ ,
所以 $ t=0 $ 或 $ t=-3 $ 或 $ t=-4 $ ,
但 $ |-3+(-4)|\notin B $ , $ |-4+0|\notin B $ ,
所以满足条件的集合 $ A $ 有 $ {0,1,2} $ , $ {-3 {\rm ,1} $ , $ 2} $ , $ {-3 {\rm ,0,1} $ , $ 2} $ , $ {-4 {\rm ,1} $ , $ 2} $ .
(2) (ⅰ) 【证明】已知 $ -1\in A $ , $ x $ , $ y\in A $ , $ y > x > 0 $ , $ A\subseteq \mathrm{Z} $ ,
由①知, $ |y+(-1)|=y-1\in B $ , $ |x+(-1)|=x-1\in B $ ,
由②知, $ |y-1-(x-1)|=y-x\in A $ .
(ⅱ) 因为 $ B $ 中至少有3个元素, $ B\subseteq \mathrm{Z} $ ,
不妨设 $ B={p $ , $ q $ , $ r} $ ,其中 $ p < q < r $ , $ p $ , $ q $ , $ r $ 互为不相等的整数,
则 $ |q-p| $ , $ |r-p| $ , $ |r-q|\in A $ ,且 $ 0 < q-p < r-p $ ,
所以 $ A $ 中至少存在两个正整数,则不妨设 $ m $ , $ n\in {\boldsymbol{N}}^{\ast } $ , $ m $ , $ n\in A $ , $ m < n $ ,又 $ -1\in A $ ,
由①知, $ m-1=m+(-1)\in B $ , $ n-1=n+(-1)\in B $ , $ n+m\in B $ ,
由②知, $ n+m-(m-1)=n+1\in A $ , $ n+m-(n-1)=m+1\in A $ ,
故由 $ m $ , $ n\in {\boldsymbol{N}}^{\ast } $ , $ m < n $ , $ m $ , $ n\in A $ , $ -1\in A $ ,可推出 $ m+1 $ , $ n+1\in A $ ,
同理由 $ m+1 $ , $ n+1\in A $ 可推出 $ m+2 $ , $ n+2\in A $ ,
由 $ m+2 $ , $ n+2\in A $ ,可推出 $ m+3 $ , $ n+3\in A $ , $ \cdots $ ,
因此所有大于或等于 $ m $ 的正整数,都属于 $ A $ .
因为 $ m $ , $ m+1 $ , $ m+2 $ , $ \cdots $ , $ 2m-1\in A $ ,
由(ⅰ)知, $ m+1-m=1\in A $ , $ m+2-m=2\in A $ , $ \cdots $ , $ 2m-1-m=m-1\in A $ .
综上,任意的正整数都属于 $ A $ ,所以 $ {\mathrm{N}}^{\ast }\subseteq A $ .
11.已知非空实数集 $ S $ , $ T $ 满足:若 $ x\in S $ ,则 $ \dfrac{x-1}{x+1}\in S $ ;若 $ y\in T $ ,则 $ \dfrac{y-1}{y}\in T $ .
(1) 若 $ 3\in S $ ,直接写出 $ S $ 中一定包含的元素;
(2) 若 $ T $ 由三个元素组成,且所有元素之和为 $ \dfrac{3}{2} $ ,求 $ T $ ;
(3) 若 $ S\cup T $ 由2 024个元素组成,求 $ S\cap T $ 的元素个数的最大值.
(1) 【解】由题意可得, $ x\in S $ ,则 $ \dfrac{x-1}{x+1}\in S $ ,于是 $ 3\in S $ ,则 $ \dfrac{3-1}{3+1}=\dfrac{1}{2}\in S $ ,则 $ \dfrac{\dfrac{1}{2}-1}{\dfrac{1}{2}+1}=-\dfrac{1}{3}\in S $ ,则 $ \dfrac{-\dfrac{1}{3}-1}{-\dfrac{1}{3}+1}=-2\in S $ ,则 $ \dfrac{-2-1}{-2+1}=3\in S $ ,
所以 $ S $ 中一定包含的元素为 $ {\rm 3,} \dfrac{1}{2} $ , $ -\dfrac{1}{3} $ , $ -2 $ .
(2) 【解】令 $ y=t $ ,则 $ \dfrac{t-1}{t}\in T $ , $ \dfrac{\dfrac{t-1}{t}-1}{\dfrac{t-1}{t}}=\dfrac{-1}{t-1}\in T $ , $ \dfrac{\dfrac{-1}{t-1}-1}{\dfrac{-1}{t-1}}=t\in T $ ,
因为 $ t=\dfrac{t-1}{t} $ , $ t=\dfrac{-1}{t-1} $ , $ \dfrac{t-1}{t}=\dfrac{-1}{t-1} $ 都可化为 $ {t}^{2}-t+1=0 $ , $ \mathrm{\Delta }=1-4=-3 < 0 $ ,则 $ {t}^{2}-t+1=0 $ 无解,
故 $ t $ , $ \dfrac{t-1}{t} $ , $ \dfrac{-1}{t-1} $ 为 $ T $ 中的三个元素.
因为所有元素之和为 $ \dfrac{3}{2} $ ,
所以 $ t+\dfrac{t-1}{t}+\dfrac{-1}{t-1}=\dfrac{3}{2} $ ,
整理得 $ {t}^{3}-\dfrac{3}{2}{t}^{2}-\dfrac{3}{2}t+1=0 $ ,
即 $ (t+1)({t}^{2}-\dfrac{5}{2}t+1)=0 $ ,
解得 $ t=-1 $ 或 $ t=2 $ 或 $ t=\dfrac{1}{2} $ ,
所以 $ T={-1,2,\dfrac{1}{2}} $ .
(3) 【解】若 $ s\in S $ ,则 $ \dfrac{s-1}{s+1}\in S $ , $ \dfrac{\dfrac{s-1}{s+1}-1}{\dfrac{s-1}{s+1}+1}=-\dfrac{1}{s}\in S $ , $ \dfrac{-\dfrac{1}{s}-1}{-\dfrac{1}{s}+1}=\dfrac{-s-1}{s-1}\in S $ , $ \dfrac{\dfrac{-s-1}{s-1}-1}{\dfrac{-s-1}{s-1}+1}=s\in S $ ,
而 $ \dfrac{s-1}{s+1}=s $ , $ \dfrac{s-1}{s+1}=-\dfrac{1}{s} $ , $ s=-\dfrac{1}{s} $ , $ \dfrac{-s-1}{s-1}=s $ , $ \dfrac{-s-1}{s-1}=-\dfrac{1}{s} $ , $ \dfrac{-s-1}{s-1}=\dfrac{s-1}{s+1} $ 均无解,
所以数集 $ S $ 以 $ {s,\dfrac{s-1}{s+1},\dfrac{-s-1}{s-1},-\dfrac{1}{s}} $ 的形式出现,即4个数为一组出现,组与组之间无公共元素, $ {\rm 0,} -1 $ , $ 1\notin S $ .
由(2)知数集 $ T $ 以 $ {t,\dfrac{t-1}{t},\dfrac{-1}{t-1}} $ 的形式出现,即3个数为一组出现,组与组之间无公共元素, $ {\rm 0,} 1\notin T $ ,
于是数集 $ S $ , $ T $ 的元素个数分别是4和3的倍数,且当 $ s=t $ 时, $ \dfrac{s-1}{s+1}\ne \dfrac{t-1}{t} $ , $ \dfrac{s-1}{s+1}\ne \dfrac{-1}{t-1} $ , $ \dfrac{-s-1}{s-1}\ne \dfrac{t-1}{t} $ , $ \dfrac{-s-1}{s-1}\ne \dfrac{-1}{t-1} $ , $ -\dfrac{1}{s}\ne \dfrac{t-1}{t} $ , $ -\dfrac{1}{s}\ne \dfrac{-1}{t-1} $ ,
而4和3互素,因此数集 $ S $ , $ T $ 中各组最多只能有1个公共元素.
设集合 $ S $ 中共有 $ m $ 个元素,满足 $ m $ 是4的正整数倍,其中有 $ n $ 个元素在 $ S\cap T $ 中,满足 $ n\leqslant m $ ,
由以上分析知,这 $ n $ 个元素在集合 $ T $ 中归属于不同组内,则集合 $ T $ 中有 $ 3n $ 个元素,同时在 $ T $ 内还有 $ k $ 个元素,并满足 $ k $ 是3的整数倍, $ k\geqslant 0 $ ,
则 $ 2024=m+2n+k\geqslant 3n+k\geqslant 3n $ ,
解得 $ n\leqslant 674 $ ,当 $ n=674 $ 时,符合条件的整数 $ m=676 $ , $ k=0 $ ,
所以 $ S\cap T $ 的元素个数的最大值是674.