2.2 基本不等式
一、刷基础
1.已知实数a,b,则 “ab⩾0” 是“ $ a+b\geqslant 2\sqrt{ab} $ ”的 ( )
A.充分不必要条件
B.必要不充分条件
C.充要条件
D.既不充分也不必要条件
答案:B
解析:因为 $ a+b\geqslant 2\sqrt{ab} $ 等价于( $ \sqrt{a}- $ $ \sqrt{b} $ )2⩾0,所以a⩾0,b⩾0,所以“ab⩾0”是“ $ a+b\geqslant 2\sqrt{ab} $ ”的必要不充分条件.故选B.
2.若 $ a $ , $ b\in \boldsymbol{R} $ ,且 $ ab > 0 $ ,则下列不等式中,恒成立的是( )
A. $ a+b\geqslant 2\sqrt{ab} $
B. $ \dfrac{a}{b}+\dfrac{b}{a}\geqslant 2 $
C. $ ab\geqslant {\left(\dfrac{a+b}{2}\right) ^ {2}} $
D. $ \dfrac{1}{a}+\dfrac{1}{b}\geqslant \dfrac{2}{\sqrt{ab}} $
答案:B
解析:对于 $ \mathrm{A} $ ,若 $ a=-1 $ , $ b=-1 $ ,则 $ a+b=-2 < 2\sqrt{ab}=2 $ ,故 $ \mathrm{A} $ 错误;
对于 $ \mathrm{B} $ ,由 $ ab > 0 $ ,可知 $ \dfrac{b}{a} > 0 $ , $ \dfrac{a}{b} > 0 $ ,则 $ \dfrac{a}{b}+\dfrac{b}{a}\geqslant 2\sqrt{\dfrac{a}{b}\cdot \dfrac{b}{a}}=2 $ ,当且仅当 $ a=b $ 时取等号,故 $ \mathrm{B} $ 正确;
对于 $ \mathrm{C} $ ,因为 $ (a-b)^{2}\geqslant 0 $ ,所以 $ {a}^{2}+{b}^{2}\geqslant 2ab $ ,所以 $ \dfrac{{a}^{2}+{b}^{2}+2ab}{4}\geqslant ab $ ,即 $ {\left(\dfrac{a+b}{2}\right) ^ {2}}\geqslant ab $ ,当且仅当 $ a=b $ 时取等号,故 $ \mathrm{C} $ 错误;
对于 $ \mathrm{D} $ ,由 $ \mathrm{A} $ 分析,可知当 $ a $ , $ b $ 同为负数时, $ \dfrac{1}{a}+\dfrac{1}{b} < 0 < \dfrac{2}{\sqrt{ab}} $ ,故 $ \mathrm{D} $ 错误.故选 $ \mathrm{B} $ .
3.已知 $ a > 0 $ , $ b > 0 $ ,则 $ \dfrac{a+b}{2} $ , $ \sqrt{ab} $ , $ \sqrt{\dfrac{{a}^{2}+{b}^{2}}{2}} $ , $ \dfrac{2ab}{a+b} $ 中最大的是( )
A. $ \sqrt{\dfrac{{a}^{2}+{b}^{2}}{2}} $
B. $ \sqrt{ab} $
C. $ \dfrac{a+b}{2} $
D. $ \dfrac{2ab}{a+b} $
答案:A
解析:因为 $ a > 0 $ , $ b > 0 $ ,所以 $ \dfrac{2ab}{a+b}\leqslant \dfrac{2ab}{2\sqrt{ab}}=\sqrt{ab} $ , $ \sqrt{ab}\leqslant \dfrac{a+b}{2} $ , $ \sqrt{\dfrac{{a}^{2}+{b}^{2}}{2}}=\sqrt{\dfrac{2({a}^{2}+{b}^{2})}{4}}\geqslant \sqrt{\dfrac{{\left(a+b\right) ^ {2}}}{4}}=\dfrac{a+b}{2} $ ,当且仅当 $ a=b $ 时,等号成立,
则 $ \dfrac{2ab}{a+b}\leqslant \sqrt{ab}\leqslant \dfrac{a+b}{2}\leqslant \sqrt{\dfrac{{a}^{2}+{b}^{2}}{2}} $ .故选 $ \mathrm{A} $ .
4.已知实数 $ a $ , $ b $ , $ c $ 满足 $ c-b=a+\dfrac{2}{a}-2 $ , $ c+b=2{a}^{2}+2a+\dfrac{2}{a} $ ,且 $ a > 0 $ ,则 $ a $ , $ b $ , $ c $ 的大小关系是( )
A. $ b > c > a $
B. $ c > b > a $
C. $ a > c > b $
D. $ c > a > b $
答案:B
解析:因为 $ a > 0 $ ,由基本不等式得 $ c-b=a+\dfrac{2}{a}-2\geqslant 2\sqrt{a\cdot \dfrac{2}{a}}-2=2\sqrt{2}-2 $ ,当且仅当 $ a=\sqrt{2} $ 时等号成立,又 $ 2\sqrt{2}-2 > 0 $ ,
所以 $ c > b $ .又 $ c+b=2{a}^{2}+2a+\dfrac{2}{a} $ , $ c-b=a+\dfrac{2}{a}-2 $ ,两式相减得, $ 2b=2{a}^{2}+2a+\dfrac{2}{a}-a-\dfrac{2}{a}+2=2{a}^{2}+a+2 $ ,故 $ b={a}^{2}+\dfrac{1}{2}a+1 $ ,所以 $ b-a={a}^{2}-\dfrac{1}{2}a+1={\left(a-\dfrac{1}{4}\right) ^ {2}}+\dfrac{15}{16} > 0 $ ,故 $ b > a $ ,所以 $ c > b > a $ .故选 $ \mathrm{B} $ .
5.若 $ a > 1 $ ,则 $ 4a+\dfrac{1}{a-1} $ 的最小值为( )
A.4
B.6
C.8
D.无最小值
答案:C
解析:若 $ a > 1 $ ,则 $ 4a+\dfrac{1}{a-1}=4(a-1)+\dfrac{1}{a-1}+4\geqslant 2\sqrt{4(a-1)\cdot \dfrac{1}{a-1}}+4=8 $ ,
当且仅当 $ 4(a-1)=\dfrac{1}{a-1} $ ,即 $ a=\dfrac{3}{2} $ 时,等号成立,所以 $ 4a+\dfrac{1}{a-1} $ 的最小值为8.故选 $ \mathrm{C} $ .
6.已知 $ 0 < a < \sqrt{2} $ ,则 $ a\sqrt{2-{a}^{2}} $ 的最大值为( )
A. $ \dfrac{1}{2} $
B. $ \dfrac{\sqrt{2}}{2} $
C.1
D. $ \sqrt{2} $
答案:C
解析:因为 $ 0 < a < \sqrt{2} $ ,所以 $ 2-{a}^{2} > 0 $ ,
所以 $ a\sqrt{2-{a}^{2}}=\sqrt{{a}^{2}(2-{a}^{2})}\leqslant \dfrac{{a}^{2}+(2-{a}^{2})}{2}=1 $ ,当且仅当 $ {a}^{2}=2-{a}^{2} $ ,即 $ a=1 $ 时取等号,所以 $ a\sqrt{2-{a}^{2}} $ 的最大值为1.故选 $ \mathrm{C} $ .
7.设 $ \dfrac{1}{2} < x < 2 $ ,则 $ \dfrac{1}{2x-1}+\dfrac{32}{2-x} $ 的最小值为( )
A.81
B.27
C.9
D.3
答案:B
解析:由于 $ \dfrac{1}{2} < x < 2 $ ,故 $ 2x-1 > 0 $ , $ 2-x > 0 $ ,故 $ \dfrac{1}{2x-1}+\dfrac{32}{2-x}=\dfrac{1}{2x-1}+\dfrac{64}{4-2x}=\dfrac{1}{3}(\dfrac{1}{2x-1}+\dfrac{64}{4-2x})[(2x-1)+(4-2x)]=\dfrac{1}{3}[65+\dfrac{4-2x}{2x-1}+\dfrac{64(2x-1)}{4-2x}]\geqslant \dfrac{1}{3}[65+2\sqrt{\dfrac{4-2x}{2x-1}\cdot \dfrac{64(2x-1)}{4-2x}}]=\dfrac{1}{3}×(65+2×8)=27 $ ,当且仅当 $ \dfrac{4-2x}{2x-1}=\dfrac{64(2x-1)}{4-2x} $ ,即 $ x=\dfrac{2}{3} $ 时等号成立,故所求最小值为27,故选 $ \mathrm{B} $ .
8.已知 $ x > 0 $ , $ y > 0 $ ,且 $ x+2y=4 $ ,则 $ (1+x)(1+2y) $ 的最大值为( )
A.36
B.4
C.16
D.9
答案:D
解析:由题意,得 $ (1+x)+(1+2y)=6 $ , $ 1+x > 1 $ , $ 1+2y > 1 $ ,所以 $ (1+x)(1+2y)\leqslant {[\dfrac{(1+x)+(1+2y)}{2}]}^{2}=9 $ ,当且仅当 $ \begin{cases}1+x=1+2y,\\ x+2y=4,\end{cases} $ 即 $ \begin{cases}x=2,\\ y=1\end{cases} $ 时取等号.故选 $ \mathrm{D} $ .
9.关于 $ x $ 的方程 $ {x}^{2}-ax+b-1=0 $ 有两个相等的正根,则 $ \dfrac{3a+2b}{a+b} $ ( )
A.有最大值 $ \dfrac{11}{5} $
B.有最大值 $ \dfrac{5}{2} $
C.有最小值 $ \dfrac{11}{5} $
D.有最小值 $ \dfrac{5}{2} $
答案:B
解析: $ \because $ 关于 $ x $ 的方程 $ {x}^{2}-ax+b-1=0 $ 有两个相等的正根,
$ \therefore \begin{cases}a > 0,\\ b-1 > 0,\\ \mathrm{\Delta }={a}^{2}-4(b-1)=0,\end{cases}\therefore b=\dfrac{{a}^{2}}{4}+1 $ , $ a > 0 $ ,
$ \therefore \dfrac{3a+2b}{a+b}=2+\dfrac{a}{a+b}=2+\dfrac{a}{\dfrac{{a}^{2}}{4}+a+1}=2+\dfrac{1}{\dfrac{a}{4}+\dfrac{1}{a}+1}\leqslant 2+\dfrac{1}{2\sqrt{\dfrac{a}{4}\cdot \dfrac{1}{a}}+1}=2+\dfrac{1}{2}=\dfrac{5}{2} $ ,当且仅当 $ a=b=2 $ 时取等号, $ \therefore \dfrac{3a+2b}{a+b} $ 有最大值 $ \dfrac{5}{2} $ .故选 $ \mathrm{B} $ .
10.(多选)若 $ x > 0 $ , $ y > 0 $ ,且 $ 2x+y=xy $ ,则( )(多选)
A. $ \dfrac{2}{x}+\dfrac{2}{y} > 1 $
B. $ x+2y+xy\geqslant 9+6\sqrt{2} $
C. $ xy\leqslant 8 $
D. $ 2xy-2x-y\geqslant 8 $
答案:ABD
解析: $ \because x > 0 $ , $ y > 0 $ , $ 2x+y=xy $ , $ \therefore \dfrac{1}{x}+\dfrac{2}{y}=1 $ , $ \therefore \dfrac{2}{x}+\dfrac{2}{y} > \dfrac{1}{x}+\dfrac{2}{y}=1 $ , $ \mathrm{A} $ 正确;
$ x+2y+xy=3x+3y=(3x+3y)(\dfrac{1}{x}+\dfrac{2}{y})=9+\dfrac{3y}{x}+\dfrac{6x}{y}\geqslant 9+6\sqrt{2} $ ,当且仅当 $ \sqrt{2}x=y $ 且 $ 2x+y=xy $ ,即 $ x=1+\sqrt{2} $ , $ y=2+\sqrt{2} $ 时等号成立, $ \mathrm{B} $ 正确;
$ 2x+y=xy\geqslant 2\sqrt{2xy} $ ,解得 $ xy\geqslant 8 $ ,当且仅当 $ y=2x $ 且 $ 2x+y=xy $ ,即 $ x=2 $ , $ y=4 $ 时取等号, $ \mathrm{C} $ 错误;
由 $ \mathrm{A} $ 的分析知 $ \dfrac{1}{x}+\dfrac{2}{y}=1 $ ,则 $ 2xy-2x-y=2x+y=(2x+y)(\dfrac{1}{x}+\dfrac{2}{y})=4+\dfrac{y}{x}+\dfrac{4x}{y}\geqslant 4+2\sqrt{\dfrac{y}{x}\cdot \dfrac{4x}{y}}=8 $ ,当且仅当 $ y=2x $ 且 $ \dfrac{1}{x}+\dfrac{2}{y}=1 $ ,即 $ x=2 $ , $ y=4 $ 时取等号,故 $ \mathrm{D} $ 正确.故选 $ \mathrm{A}\mathrm{B}\mathrm{D} $ .
11.已知 $ a $ , $ b $ , $ c $ 均为正实数.
(1) 证明: $ a+b+c\geqslant \sqrt{2ab}+\sqrt{2bc} $ ;
(2) 证明 $ \dfrac{a+b+c}{3}\geqslant \sqrt[3]{abc} $ ,并求 $ y=2x+\dfrac{1}{{\left(x-2\right) ^ {2}}}(x > 2) $ 的最小值.
答案:(1) 【证明】由基本不等式得 $ a+\dfrac{b}{2}\geqslant \sqrt{2ab} $ , $ \dfrac{b}{2}+c\geqslant \sqrt{2bc} $ ,
两个不等式相加得 $ a+b+c\geqslant \sqrt{2ab}+\sqrt{2bc} $ ,
当且仅当 $ a=\dfrac{b}{2}=c $ 时“ $ = $ ”成立,问题得证.
(2) 【解】 $ {a}^{3}+{b}^{3}+{c}^{3}-3abc={\left(a+b\right) ^ {3}}-3{a}^{2}b-3a{b}^{2}+{c}^{3}-3abc $
$ ={\left(a+b\right) ^ {3}}+{c}^{3}-3{a}^{2}b-3a{b}^{2}-3abc $
$ = (a+b+c ) [ (a+b)^{2}- (a+b )c+{c}^{2} ]-3ab (a+b+c ) $
$ =(a+b+c)({a}^{2}+2ab+{b}^{2}-ac-bc+{c}^{2}-3ab) $
$ =(a+b+c)({a}^{2}+{b}^{2}+{c}^{2}-ab-bc-ca) $
$ =\dfrac{1}{2} (a+b+c ) [ (a-b)^{2}+{\left(b-c \right) ^ {2}}+{\left(c-a \right) ^ {2}} ]\geqslant 0 $ ,
当且仅当 $ a=b=c $ 时等号成立,
所以不等式 $ {a}^{3}+{b}^{3}+{c}^{3}\geqslant 3abc $ 成立,
所以 $ a+b+c={\left(\sqrt[3]{a}\right) ^ {3}}+{\left(\sqrt[3]{b}\right) ^ {3}}+{\left(\sqrt[3]{c}\right) ^ {3}}\geqslant 3×\sqrt[3]{a}×\sqrt[3]{b}×\sqrt[3]{c}=3\sqrt[3]{abc} $ ,
所以 $ \dfrac{a+b+c}{3}\geqslant \sqrt[3]{abc} $ ,当且仅当 $ a=b=c $ 时取等号,
故不等式 $ \dfrac{a+b+c}{3}\geqslant \sqrt[3]{abc} $ 成立.
因为 $ x > 2 $ ,所以 $ x-2 > 0 $ , $ y=2x+\dfrac{1}{{\left(x-2\right) ^ {2}}}=(x-2)+(x-2)+\dfrac{1}{{\left(x-2\right) ^ {2}}}+4\geqslant 3\sqrt[3]{(x-2)\cdot (x-2)\cdot \dfrac{1}{{\left(x-2\right) ^ {2}}}}+4=7 $ ,
当且仅当 $ x-2=\dfrac{1}{{\left(x-2\right) ^ {2}}} $ ,即 $ x=3 $ 时,等号成立,所以 $ {y}_{ \min }=7 $ .
解析:
12.已知 $ x > 0 $ , $ y > 0 $ , $ x+2y=1 $ ,证明: $ (1+\dfrac{2}{x})(1+\dfrac{1}{y})\geqslant 25 $ .
答案:【证明】 $ \because x > 0 $ , $ y > 0 $ , $ x+2y=1 $ , $ \therefore (1+\dfrac{2}{x})(1+\dfrac{1}{y})=(1+\dfrac{2x+4y}{x})(1+\dfrac{x+2y}{y})=(3+\dfrac{4y}{x})(3+\dfrac{x}{y})=13+(\dfrac{12y}{x}+\dfrac{3x}{y})\geqslant 13+2\sqrt{\dfrac{12y}{x}\cdot \dfrac{3x}{y}}=25 $ ,当且仅当 $ \dfrac{4y}{x}=\dfrac{x}{y} $ ,即 $ y=\dfrac{1}{4} $ , $ x=\dfrac{1}{2} $ 时,等号成立, $ \therefore (1+\dfrac{2}{x})(1+\dfrac{1}{y})\geqslant 25 $ .
解析:
13.制作一个面积为 $ 2{\mathrm{m}}^{2} $ ,形状为直角三角形的铁支架框,有下列四种长度的铁管供选择,较经济(够用,又耗材最少)的是( )
A. $ 6.2\mathrm{m} $
B. $ 6.8\mathrm{m} $
C. $ 7\mathrm{m} $
D. $ 7.2\mathrm{m} $
答案:C
解析:设两直角边的长度分别为 $ a $ , $ b $ , $ a > 0 $ , $ b > 0 $ ,则 $ ab=4 $ ,铁支架框的周长 $ l=a+b+\sqrt{{a}^{2}+{b}^{2}}\geqslant 2\sqrt{ab}+\sqrt{2ab}=4+2\sqrt{2}\approx 6.828 $ ,当且仅当 $ a=b=2 $ 时取等号.
故选 $ \mathrm{C} $ .
14.某企业2024年年初花费64万元购进一台新的设备,并立即投入使用,该设备使用后,每年的总收入预计为30万元,设备使用 $ x(x\in {\boldsymbol{N}}^{\ast }) $ 年后该设备的维修保养费用为 $ {x}^{2}+4x $ 万元,盈利总额为 $ y $ 万元.
(1) 求 $ y $ 关于 $ x $ 的函数关系式;
(2) 求该设备的年平均盈利额的最大值(年平均盈利额 $ = $ 盈利总额 $ ÷ $ 使用年数).
答案:(1) 【解】根据题意, $ y=30x-64-({x}^{2}+4x)=-{x}^{2}+26x-64 $ ,
故 $ y $ 关于 $ x $ 的函数关系式为 $ y=-{x}^{2}+26x-64(x\in {\boldsymbol{N}}^{\ast }) $ .
(2) 【解】由(1)知盈利总额 $ y=-{x}^{2}+26x-64(x\in {\boldsymbol{N}}^{\ast }) $ ,
则年平均盈利额 $ W=\dfrac{-{x}^{2}+26x-64}{x} $ ,
则 $ W=26-(x+\dfrac{64}{x}) $ ,因为 $ x+\dfrac{64}{x}\geqslant 2\sqrt{x\cdot \dfrac{64}{x}}=16 $ (当且仅当 $ x=8 $ 时取等号),所以 $ W\leqslant 26-16=10 $ 万元,
故该设备使用8年后年平均盈利额取得最大值,最大值为10万元.
解析:
15.对于任意 $ 0 < x < 4 $ , $ m > \dfrac{x}{{x}^{2}+1} $ 恒成立,则( )
A. $ m > \dfrac{2}{5} $
B. $ m > \dfrac{3}{5} $
C. $ m > \dfrac{3}{10} $
D. $ m > \dfrac{1}{2} $
答案:D
解析:对于任意 $ 0 < x < 4 $ , $ m > \dfrac{x}{{x}^{2}+1} $ 恒成立,则 $ m > {(\dfrac{x}{{x}^{2}+1})}_{ \max } $ ,而 $ \dfrac{x}{{x}^{2}+1}=\dfrac{1}{x+\dfrac{1}{x}}\leqslant \dfrac{1}{2\sqrt{x\cdot \dfrac{1}{x}}}=\dfrac{1}{2} $ ,当且仅当 $ x=1 $ 时取等号,所以 $ m > \dfrac{1}{2} $ .故选 $ \mathrm{D} $ .
16.已知 $ a > 0 $ , $ b > 0 $ ,且 $ ab=1 $ ,不等式 $ \dfrac{1}{a}+\dfrac{1}{b}+\dfrac{m}{a+b}\geqslant 4 $ 恒成立,则正实数 $ m $ 的取值范围是( )
A. $ {m|m\geqslant 2} $
B. $ {m|m\geqslant 4} $
C. $ {m|m\geqslant 6} $
D. $ {m|m\geqslant 8} $
答案:B
解析:由题设得 $ m\geqslant 4 (a+b )- (\dfrac{1}{a}+\dfrac{1}{b} ) (a+b )=4 (a+b )- (a+b)^{2} $ 恒成立,而 $ 4 (a+b )- (a+b)^{2}=4- (a+b-2)^{2} $ ,又 $ a+b\geqslant 2\sqrt{ab}=2 $ ,当且仅当 $ a=b=1 $ 时等号成立,所以 $ 4 (a+b )- (a+b)^{2}\leqslant 4 $ ,当且仅当 $ a=b=1 $ 时等号成立,故 $ m\geqslant 4 $ .故选 $ \mathrm{B} $ .
17.已知正实数 $ x $ , $ y $ 满足 $ 3x+y=1 $ ,若不等式 $ \dfrac{y}{x}+\dfrac{1}{y}\leqslant m $ 有解,则实数 $ m $ 的取值范围是 .
答案: $ {m|m\geqslant 2\sqrt{3}+1} $
解析:因为正实数 $ x $ , $ y $ 满足 $ 3x+y=1 $ ,
所以 $ \dfrac{y}{x}+\dfrac{1}{y}=\dfrac{y}{x}+\dfrac{3x+y}{y}=\dfrac{y}{x}+\dfrac{3x}{y}+1\geqslant 2\sqrt{\dfrac{y}{x}\cdot \dfrac{3x}{y}}+1=2\sqrt{3}+1 $ ,
当且仅当 $ \dfrac{y}{x}=\dfrac{3x}{y} $ ,即 $ x=\dfrac{3-\sqrt{3}}{6} $ , $ y=\dfrac{\sqrt{3}-1}{2} $ 时取等号,
所以 $ \dfrac{y}{x}+\dfrac{1}{y} $ 的最小值为 $ 2\sqrt{3}+1 $ .因为不等式 $ \dfrac{y}{x}+\dfrac{1}{y}\leqslant m $ 有解,
所以 $ m\geqslant 2\sqrt{3}+1 $ ,即实数 $ m $ 的取值范围为 $ {m|m\geqslant 2\sqrt{3}+1} $ .
18. $ 2+x+\dfrac{5}{x}(x < 0) $ 的最大值为 .
解析: $ \because x < 0 $ , $ \therefore -x > 0 $ ,
$ \therefore 2+x+\dfrac{5}{x}=2-(-x-\dfrac{5}{x}) $ .
又 $ \because -x-\dfrac{5}{x}\geqslant 2\sqrt{(-x)\cdot (-\dfrac{5}{x})}=2\sqrt{5} $ , $ \therefore 2+x+\dfrac{5}{x}=2-(-x-\dfrac{5}{x})\leqslant 2-2\sqrt{5} $ ,当且仅当 $ -x=-\dfrac{5}{x} $ ,且 $ x < 0 $ ,即 $ x=-\sqrt{5} $ 时,等号成立.
$ \therefore 2+x+\dfrac{5}{x}(x < 0) $ 的最大值为 $ 2-2\sqrt{5} $ .
19.以下结论正确的是( )(多选)
A. $ y=x+\dfrac{1}{x} $ 的最小值是2
B. $ y=x(2-x)(0 < x < 2) $ 的最大值是1
C. $ y=\sqrt{{x}^{2}+3}+\dfrac{1}{\sqrt{{x}^{2}+3}} $ 的最小值是2
D.存在 $ a $ ,使得不等式 $ a+\dfrac{1}{a}\leqslant -2 $ 成立
答案:BD
解析:对于 $ \mathrm{A} $ ,当 $ x < 0 $ 时,结论显然不成立,故 $ \mathrm{A} $ 错误;
对于 $ \mathrm{B} $ ,由 $ 0 < x < 2 $ ,得 $ x > 0 $ , $ 2-x > 0 $ ,所以 $ x(2-x)\leqslant {\left(\dfrac{x+2-x}{2}\right) ^ {2}}=1 $ ,当且仅当 $ 2-x=x $ ,即 $ x=1 $ 时等号成立,故 $ \mathrm{B} $ 正确;
对于 $ \mathrm{C} $ , $ y=\sqrt{{x}^{2}+3}+\dfrac{1}{\sqrt{{x}^{2}+3}}\geqslant 2\sqrt{1}=2 $ ,当且仅当 $ \sqrt{{x}^{2}+3}=\dfrac{1}{\sqrt{{x}^{2}+3}} $ ,即 $ {x}^{2}+3=1 $ 时取等号,又方程无实数解,故取不到等号,故 $ \mathrm{C} $ 错误;
对于 $ \mathrm{D} $ ,当 $ a=-2 $ 时, $ a+\dfrac{1}{a}=-\dfrac{5}{2}\leqslant -2 $ ,即存在 $ a $ ,使得 $ a+\dfrac{1}{a}\leqslant -2 $ 成立,故 $ \mathrm{D} $ 正确.故选 $ \mathrm{B}\mathrm{D} $ .
20.已知 $ x > 0 $ , $ y > 0 $ ,且 $ x+y=1 $ ,则 $ p=x+\dfrac{1}{x}+y+\dfrac{1}{y} $ 的最小值为( )
A.3
B.4
C.5
D.6
答案:C
解析: $ p=x+\dfrac{x+y}{x}+y+\dfrac{x+y}{y}=3+\dfrac{y}{x}+\dfrac{x}{y}\geqslant 3+2\sqrt{\dfrac{y}{x}\cdot \dfrac{x}{y}}=5 $ ,当且仅当 $ x=y=\dfrac{1}{2} $ 时,等号成立.
二、刷能力
1.《几何原本》卷2的几何代数法(以几何方法研究代数问题)成了后来西方数学家处理问题的重要依据.通过这一原理,很多的代数的公理或定理都能够通过图形实现证明,也称之为无字证明.现有如图所示图形,点 $ F $ 在半圆 $ O $ 上,点 $ C $ 在直径 $ AB $ 上,且 $ OF\perp AB $ ,设 $ AC=a $ , $ BC=b $ ,则该图形可以完成的无字证明为( )
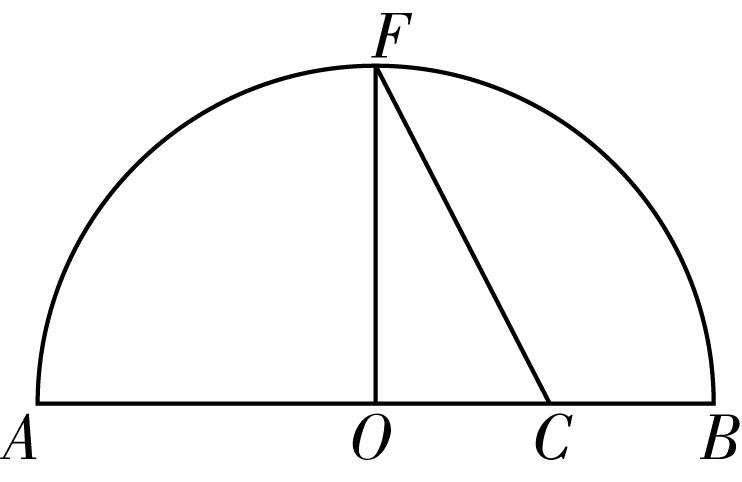
A. $ \dfrac{a+b}{2} > \sqrt{ab}(a > b > 0) $
B. $ {a}^{2}+{b}^{2} > 2ab(a > b > 0) $
C. $ \dfrac{2ab}{a+b} < \sqrt{ab}(a > b > 0) $
D. $ \dfrac{a+b}{2} < \sqrt{\dfrac{{a}^{2}+{b}^{2}}{2}}(a > b > 0) $
答案:D
解析:由图形可知, $ OF=\dfrac{AC+BC}{2}=\dfrac{a+b}{2} $ , $ OC=AC-OA=a-\dfrac{a+b}{2}=\dfrac{a-b}{2}(a > b > 0) $ ,
由勾股定理可得 $ CF=\sqrt{O{F}^{2}+O{C}^{2}}=\sqrt{{\left(\dfrac{a+b}{2}\right) ^ {2}}+{\left(\dfrac{a-b}{2}\right) ^ {2}}}=\sqrt{\dfrac{{a}^{2}+{b}^{2}}{2}} $ .
在 $ \mathrm{R}\mathrm{t}△OCF $ 中,由 $ OF < CF $ 可得 $ \dfrac{a+b}{2} < \sqrt{\dfrac{{a}^{2}+{b}^{2}}{2}}(a > b > 0) $ .故选 $ \mathrm{D} $ .
2.已知 $ a > 0 $ , $ b > 0 $ ,且 $ \dfrac{1}{a}+\dfrac{2}{b}=1 $ ,则 $ \dfrac{2}{a-1}+\dfrac{1}{b-2} $ 的最小值为( )
A.2
B. $ \sqrt{2} $
C. $ \dfrac{3\sqrt{2}}{2} $
D. $ 1+\dfrac{3\sqrt{2}}{4} $
答案:A
解析:因为 $ a > 0 $ , $ b > 0 $ ,且 $ \dfrac{1}{a}+\dfrac{2}{b}=1 $ ,
所以 $ \dfrac{1}{a}=1-\dfrac{2}{b}=\dfrac{b-2}{b} $ ,所以 $ a=\dfrac{b}{b-2} > 0 $ ,所以 $ b > 2 $ ,
所以 $ a-1=\dfrac{b}{b-2}-1=\dfrac{b-(b-2)}{b-2}=\dfrac{2}{b-2} > 0 $ ,则 $ \dfrac{2}{a-1}+\dfrac{1}{b-2}=(b-2)+\dfrac{1}{b-2}\geqslant 2\sqrt{(b-2)\cdot \dfrac{1}{b-2}}=2 $ ,
当且仅当 $ b-2=\dfrac{1}{b-2} $ ,即 $ b=3 $ 时等号成立,
所以 $ \dfrac{2}{a-1}+\dfrac{1}{b-2} $ 的最小值为2.
故选 $ \mathrm{A} $ .
3.设正实数 $ x $ , $ y $ , $ z $ 满足 $ {x}^{2}-3xy+4{y}^{2}-z=0 $ ,则当 $ \dfrac{xy}{z} $ 取得最大值时, $ \dfrac{2}{x}+\dfrac{1}{y}-\dfrac{2}{z} $ 的最大值为( )
A.9
B.1
C. $ \dfrac{9}{4} $
D.3
答案:B
解析: $ \because {x}^{2}-3xy+4{y}^{2}-z=0 $ ,
$ \therefore z={x}^{2}-3xy+4{y}^{2} $ ,又 $ x $ , $ y $ , $ z $ 均为正实数,
$ \therefore \dfrac{xy}{z}=\dfrac{xy}{{x}^{2}-3xy+4{y}^{2}}=\dfrac{1}{\dfrac{x}{y}+\dfrac{4y}{x}-3}\leqslant \dfrac{1}{2\sqrt{\dfrac{x}{y}\cdot \dfrac{4y}{x}}-3}=1 $ ,当且仅当 $ x=2y $ 时取“ $ = $ ”, $ \therefore {(\dfrac{xy}{z})}_{\mathrm{m}\mathrm{a}\mathrm{x}}=1 $ ,此时 $ x=2y $ .
$ \therefore z={x}^{2}-3xy+4{y}^{2}={\left(2y\right) ^ {2}}-3×2y\cdot y+4{y}^{2}=2{y}^{2} $ , $ \therefore \dfrac{2}{x}+\dfrac{1}{y}-\dfrac{2}{z}=\dfrac{1}{y}+\dfrac{1}{y}-\dfrac{1}{{y}^{2}}=-(\dfrac{1}{y}-1)^{2}+1\leqslant 1 $ ,当且仅当 $ y=1 $ 时取得“ $ = $ ”,满足题意. $ \therefore \dfrac{2}{x}+\dfrac{1}{y}-\dfrac{2}{z} $ 的最大值为1,当且仅当 $ x=2y=2 $ 时取“ $ = $ ”.故选B.
4.(多选)已知 $ a $ , $ b $ 均为正实数,且 $ a+b=1 $ ,则( )(多选)
A. $ ab $ 的最大值为 $ \dfrac{1}{4} $
B. $ \dfrac{b}{a}+\dfrac{2}{b} $ 的最小值为5
C. $ ({a}^{2}+\dfrac{1}{8})({b}^{2}+\dfrac{1}{8}) $ 的最小值为 $ \dfrac{1}{8} $
D. $ \dfrac{{a}^{2}}{a+2}+\dfrac{{b}^{2}}{b+1} $ 的最小值为 $ \dfrac{1}{4} $
答案:ACD
解析:对于 $ \mathrm{A} $ 选项,由基本不等式可得 $ ab\leqslant {\left(\dfrac{a+b}{2}\right) ^ {2}}=\dfrac{1}{4} $ ,
当且仅当 $ \begin{cases}a=b,\\ a+b=1,\end{cases} $ 即当 $ a=b=\dfrac{1}{2} $ 时,等号成立,所以 $ ab $ 的最大值为 $ \dfrac{1}{4} $ , $ \mathrm{A} $ 正确;
对于 $ \mathrm{B} $ 选项, $ \dfrac{b}{a}+\dfrac{2}{b}=\dfrac{b}{a}+\dfrac{2(a+b)}{b}=\dfrac{b}{a}+\dfrac{2a}{b}+2\geqslant 2\sqrt{\dfrac{b}{a}\cdot \dfrac{2a}{b}}+2=2\sqrt{2}+2 $ ,
当且仅当 $ \begin{cases}\dfrac{b}{a}=\dfrac{2a}{b},\\ a+b=1,\\ a > 0,b > 0,\end{cases} $ 即 $ \begin{cases}a=\sqrt{2}-1,\\ b=2-\sqrt{2}\end{cases} $ 时,等号成立,所以 $ \dfrac{b}{a}+\dfrac{2}{b} $ 的最小值为 $ 2\sqrt{2}+2 $ , $ \mathrm{B} $ 错误;
对于 $ \mathrm{C} $ 选项, $ ({a}^{2}+\dfrac{1}{8})({b}^{2}+\dfrac{1}{8}) $
$ ={a}^{2}{b}^{2}+\dfrac{1}{8}({a}^{2}+{b}^{2})+\dfrac{1}{64} $
$ ={a}^{2}{b}^{2}+\dfrac{1}{8}{\left(a+b\right) ^ {2}}-\dfrac{1}{4}ab+\dfrac{1}{64} $
$ ={a}^{2}{b}^{2}-\dfrac{1}{4}ab+\dfrac{1}{8}+\dfrac{1}{64} $
$ ={\left(ab-\dfrac{1}{8}\right) ^ {2}}+\dfrac{1}{8}\geqslant \dfrac{1}{8} $ ,
当且仅当 $ \begin{cases}ab=\dfrac{1}{8},\\ a+b=1,\\ a > 0,b > 0,\end{cases} $ 即 $ \begin{cases}a=\dfrac{2+\sqrt{2}}{4},\\ b=\dfrac{2-\sqrt{2}}{4}\end{cases} $ 或 $ \begin{cases}a=\dfrac{2-\sqrt{2}}{4},\\ b=\dfrac{2+\sqrt{2}}{4}\end{cases} $ 时,等号成立,
所以 $ ({a}^{2}+\dfrac{1}{8})({b}^{2}+\dfrac{1}{8}) $ 的最小值为 $ \dfrac{1}{8} $ , $ \mathrm{C} $ 正确;
对于 $ \mathrm{D} $ 选项, $ \dfrac{{a}^{2}}{a+2}+\dfrac{{b}^{2}}{b+1}=\dfrac{{\left(a+2-2\right) ^ {2}}}{a+2}+\dfrac{{\left(b+1-1\right) ^ {2}}}{b+1}=a+2-4+\dfrac{4}{a+2}+b+1-2+\dfrac{1}{b+1}=\dfrac{4}{a+2}+\dfrac{1}{b+1}-2 $ ,设 $ s=a+2 $ , $ t=b+1 $ ,可得 $ s > 0,t > 0,\mathrm{且}s+t=4 $ ,
则上式 $ =\dfrac{1}{4}(\dfrac{4}{s}+\dfrac{1}{t})(s+t)-2=\dfrac{1}{4}(5+\dfrac{4t}{s}+\dfrac{s}{t})-2\geqslant \dfrac{1}{4}(5+2\sqrt{\dfrac{4t}{s}\cdot \dfrac{s}{t}})-2=\dfrac{1}{4} $ ,
当且仅当 $ \begin{cases}s=2t,\\ s+t=4,\end{cases} $ 即 $ \begin{cases}s=\dfrac{8}{3},\\ t=\dfrac{4}{3},\end{cases} $ 即 $ \begin{cases}a=\dfrac{2}{3},\\ b=\dfrac{1}{3}\end{cases} $ 时,等号成立,
所以 $ \dfrac{{a}^{2}}{a+2}+\dfrac{{b}^{2}}{b+1} $ 的最小值为 $ \dfrac{1}{4} $ , $ \mathrm{D} $ 正确.故选 $ \mathrm{A}\mathrm{C}\mathrm{D} $ .
5.(多选)根据不等式的有关知识,下列日常生活中的说法正确的是( )(多选)
A.自来水管的横截面制成圆形而不是正方形,原因是圆的面积大于与其具有相同周长的正方形的面积
B.用一架两臂不等长的天平称黄金,先将 $ 5\mathrm{g} $ 的砝码放在天平的左盘中,取出一些黄金放在天平右盘中使天平平衡;再将 $ 5\mathrm{g} $ 的砝码放在天平右盘中,再取出一些黄金放在天平左盘中使天平平衡;最后将两次称得的黄金交给顾客,则顾客购得的黄金大于 $ 10\mathrm{g} $
C.某工厂第一年的产量为 $ A $ ,第二年的增长率为 $ a $ ,第三年的增长率为 $ b $ ,则这两年的平均增长率等于 $ \dfrac{a+b}{2} $
D.两次购买同一种物品,可以用两种不同的策略,第一种是不论物品价格升降,每次购买这种物品的数量都是一定的;第二种是不论物品价格升降,每次购买这种物品所花的钱数都是一定的.若两次购买时价格不同,则用第二种策略购买更实惠
答案:ABD
解析:对于选项 $ \mathrm{A} $ :设周长为 $ l $ , $ l > 0 $ ,则圆的面积为 $ {S}_{1}=\mathrm{\pi }{\left(\dfrac{l}{2\mathrm{\pi }}\right) ^ {2}}=\dfrac{{l}^{2}}{4\mathrm{\pi }} $ ,
正方形的面积为 $ {S}_{2}={\left(\dfrac{l}{4}\right) ^ {2}}=\dfrac{{l}^{2}}{16} $ ,因为 $ \dfrac{1}{4\mathrm{\pi }} > \dfrac{1}{16} $ , $ {l}^{2} > 0 $ ,所以 $ \dfrac{{l}^{2}}{4\mathrm{\pi }} > \dfrac{{l}^{2}}{16} $ ,即 $ {S}_{1} > {S}_{2} $ ,故 $ \mathrm{A} $ 正确;
对于选项 $ \mathrm{B} $ :设天平的左、右臂长分别为 $ {L}_{1} $ , $ {L}_{2} $ ,第一次取出 $ a \mathrm{g} $ 黄金,第二次取出 $ b \mathrm{g} $ 黄金 $ (a\ne b) $ ,则 $ \begin{cases}5{L}_{1}=a{L}_{2},\\ b{L}_{1}=5{L}_{2},\end{cases} $ 则 $ \dfrac{5}{b}=\dfrac{a}{5} $ ,所以 $ ab=25 $ ,顾客购得的黄金 $ a+b > 2\sqrt{ab}=10 $ ,故 $ \mathrm{B} $ 正确;
对于选项 $ \mathrm{C} $ :设这两年的平均增长率为 $ x $ ,则 $ A (1+a ) (1+b )=A (1+x)^{2} $ ,可得 $ x=\sqrt{(1+a)(1+b)}-1 $ ,因为 $ x+1=\sqrt{(1+a)(1+b)}\leqslant \dfrac{(1+a)+(1+b)}{2}=\dfrac{a+b}{2}+1 $ ,即 $ x\leqslant \dfrac{a+b}{2} $ ,当且仅当 $ 1+a=1+b $ ,即 $ a=b $ 时等号成立,即这两年的平均增长率不大于 $ \dfrac{a+b}{2} $ ,故 $ \mathrm{C} $ 错误;
对于选项 $ \mathrm{D} $ :按第一种策略购物,设第一次购物时的价格为 $ {p}_{1} $ 元/ $ \mathrm{k}\mathrm{g} $ ,购 $ n\mathrm{k}\mathrm{g} $ ,
第二次购物时的价格为 $ {p}_{2} $ 元/ $ \mathrm{k}\mathrm{g} $ ,购 $ n\mathrm{k}\mathrm{g} $ ,两次购物的平均价格为 $ \dfrac{{p}_{1}n+{p}_{2}n}{2n}=\dfrac{{p}_{1}+{p}_{2}}{2} $ ;
若按第二种策略购物,第一次花 $ m $ 元,能购 $ \dfrac{m}{{p}_{1}}\mathrm{k}\mathrm{g} $ 物品,第二次仍花 $ m $ 元,能购 $ \dfrac{m}{{p}_{2}}\mathrm{k}\mathrm{g} $ 物品,两次购物的平均价格为 $ \dfrac{2m}{\dfrac{m}{{p}_{1}}+\dfrac{m}{{p}_{2}}}=\dfrac{2}{\dfrac{1}{{p}_{1}}+\dfrac{1}{{p}_{2}}} $ .比较两次购物的平均价格,有 $ \dfrac{{p}_{1}+{p}_{2}}{2}-\dfrac{2}{\dfrac{1}{{p}_{1}}+\dfrac{1}{{p}_{2}}}=\dfrac{{p}_{1}+{p}_{2}}{2}-\dfrac{2{p}_{1}{p}_{2}}{{p}_{1}+{p}_{2}}=\dfrac{{\left({p}_{1}+{p}_{2}\right) ^ {2}}-4{p}_{1}{p}_{2}}{2({p}_{1}+{p}_{2})}=\dfrac{{\left({p}_{1}-{p}_{2}\right) ^ {2}}}{2({p}_{1}+{p}_{2})}\geqslant 0 $ ,当且仅当 $ {p}_{1}={p}_{2} $ 时等号成立,所以两次价格不同时,第一种策略购物的平均价格高于第二种策略购物的平均价格,因而用第二种策略更实惠,故 $ \mathrm{D} $ 正确.故选 $ \mathrm{A}\mathrm{B}\mathrm{D} $ .
6.已知 $ a > 2b > 0 $ ,那么 $ \dfrac{{a}^{4}+4}{b(a-2b)} $ 的最小值是 .
解析:因为 $ a > 2b > 0 $ ,所以 $ a-2b > 0 $ ,则 $ b(a-2b)=\dfrac{1}{2}×2b(a-2b)\leqslant \dfrac{1}{2}\cdot {\left(\dfrac{2b+a-2b}{2}\right) ^ {2}}=\dfrac{1}{8}{a}^{2} $ ,当且仅当 $ 2b=a-2b $ ,即 $ a=4b $ 时等号成立,所以 $ \dfrac{{a}^{4}+4}{b(a-2b)}\geqslant \dfrac{{a}^{4}+4}{\dfrac{1}{8}{a}^{2}}=8({a}^{2}+\dfrac{4}{{a}^{2}})\geqslant 8×2\sqrt{{a}^{2}\cdot \dfrac{4}{{a}^{2}}}=32 $ ,当且仅当 $ {a}^{2}=\dfrac{4}{{a}^{2}} $ ,即 $ {a}^{2}=2 $ 时等号成立,又 $ a > 0 $ ,所以 $ a=\sqrt{2} $ , $ b=\dfrac{\sqrt{2}}{4} $ 时, $ \dfrac{{a}^{4}+4}{b(a-2b)} $ 取得最小值32.
7.若 $ a > 0 $ , $ b > 0 $ , $ a+b=1 $ ,则 $ \dfrac{{a}^{2}+3ab}{a+2b}+\dfrac{2}{b+1}-\dfrac{1}{2b} $ 的最大值为 .
解析:因为 $ a > 0 $ , $ b > 0 $ , $ a+b=1 $ ,所以 $ a=1-b > 0 $ ,所以 $ 0 < b < 1 $ ,则 $ \dfrac{{a}^{2}+3ab}{a+2b}+\dfrac{1}{b+1}=\dfrac{a(a+3b)}{a+2b}+\dfrac{1}{b+1}=\dfrac{a(1+2b)}{1+b}+\dfrac{1}{1+b}=\dfrac{(1-b)(1+2b)+1}{1+b}=\dfrac{2+b-2{b}^{2}}{b+1}=1+\dfrac{1-2{b}^{2}}{1+b}=1+\dfrac{2-2{b}^{2}-1}{1+b}=3-2b-\dfrac{1}{1+b} $ ,
所以 $ \dfrac{{a}^{2}+3ab}{a+2b}+\dfrac{2}{b+1}-\dfrac{1}{2b}=3-2b-\dfrac{1}{1+b}+\dfrac{1}{1+b}-\dfrac{1}{2b}=3-2b-\dfrac{1}{2b}=3-(2b+\dfrac{1}{2b})\leqslant 3-2=1 $ ,
当且仅当 $ a=b=\dfrac{1}{2} $ 时取等号.
8.已知 $ {a}^{2}+ab+{b}^{2}=3 $ ,则 $ {a}^{2}+{b}^{2}-ab $ 的最大值和最小值分别为 .
解析: $ {a}^{2}+ab+{b}^{2}=3\geqslant 3ab $ ,
$ \therefore ab\leqslant 1 $ ,当且仅当 $ a=b=±1 $ 时取等号,
$ {a}^{2}+ab+{b}^{2}=3\geqslant -2ab+ab $ , $ \therefore ab\geqslant -3 $ ,
当且仅当 $ a=-b=±\sqrt{3} $ 时取等号,
$ \therefore {a}^{2}+{b}^{2}-ab=3-2ab\in [1,9] $ ,
当 $ a=b=±1 $ 时取得最小值,
当 $ a=-b=±\sqrt{3} $ 时取得最大值.
9.已知 $ M=\sqrt{\dfrac{a}{b+c}}+\sqrt{\dfrac{b}{c+a}}+\sqrt{\dfrac{c}{a+b}}(a,b,c\geqslant 0) $ ,则 $ M $ 的最大值、最小值分别为 .
解析:当 $ a\to +\mathrm{\infty } $ , $ b $ , $ c\to {0}^{+} $ 时,易得 $ M=\sqrt{\dfrac{a}{b+c}}+\sqrt{\dfrac{b}{c+a}}+\sqrt{\dfrac{c}{a+b}}\to +\mathrm{\infty } $ ,
故 $ M=\sqrt{\dfrac{a}{b+c}}+\sqrt{\dfrac{b}{c+a}}+\sqrt{\dfrac{c}{a+b}}(a,b,c\geqslant 0) $ 无最大值.
若 $ a $ , $ b $ , $ c $ 中没有0,则由基本不等式可得 $ \sqrt{\dfrac{a}{b+c}}=\dfrac{a}{\sqrt{a(b+c)}}\geqslant \dfrac{a}{\dfrac{a+b+c}{2}}=\dfrac{2a}{a+b+c} $ ,
同理可得 $ \sqrt{\dfrac{b}{c+a}}\geqslant \dfrac{2b}{a+b+c} $ , $ \sqrt{\dfrac{c}{a+b}}\geqslant \dfrac{2c}{a+b+c} $ ,故有 $ M\geqslant 2 $ ,
当且仅当 $ \begin{cases}a=b+c,\\ b=c+a,\\ c=a+b\end{cases} $ 时,等号成立,而 $ a $ , $ b $ , $ c $ 中没有0时,该方程组无实数解,故 $ M > 2 $ ;
若 $ a $ , $ b $ , $ c $ 中有0,则至多有一个0,不妨设 $ c=0 $ ,此时 $ M=\sqrt{\dfrac{a}{b}}+\sqrt{\dfrac{b}{a}}\geqslant 2 $ ,
当且仅当 $ a=b $ , $ c=0 $ 时, $ M $ 取得最小值2.
综上, $ M $ 无最大值,有最小值2.
