2.3 二次函数与一元二次方程、不等式
一、刷基础
1.设 $ x\in \boldsymbol{R} $ ,使得不等式 $ {x}^{2}-2x-8 < 0 $ 成立的一个充分不必要条件是( )
A. $ -2 < x < 4 $
B. $ x > -2 $
C. $ 2\leqslant x\leqslant 3 $
D. $ x < 4 $
答案:C
解析:由 $ {x}^{2}-2x-8 < 0 $ 即 $ (x+2)(x-4) < 0 $ ,解得 $ -2 < x < 4 $ .对比选项,只有 $ {x|2\leqslant x\leqslant 3} $ 是 $ {x|-2 < x < 4} $ 的真子集,可知不等式 $ {x}^{2}-2x-8 < 0 $ 成立的一个充分不必要条件是 $ 2\leqslant x\leqslant 3 $ .故选 $ \mathrm{C} $ .
2.下面四个不等式中解集为 $ \boldsymbol{R} $ 的是( )
A. $ -{x}^{2}+x+1\geqslant 0 $
B. $ {x}^{2}-2\sqrt{5}x+5 > 0 $
C. $ {x}^{2}+6x+10 > 0 $
D. $ 2{x}^{2}-3x+4 < 0 $
答案:C
解析:利用“ $ \mathrm{\Delta } $ ”判断.在不等式 $ {x}^{2}+6x+10 > 0 $ 中,对应一元二次方程的判别式 $ \mathrm{\Delta }={6}^{2}-40 < 0 $ , $ \therefore $ 该不等式的解集为 $ \boldsymbol{R} $ ,其他可类似判断.故选 $ \mathrm{C} $ .
3.不等式 $ 0\leqslant {x}^{2}-2x-3 < 5 $ 的解集为 .
答案: $ {x|-2 < x\leqslant -1 $ 或 $ 3\leqslant x < 4} $
解析:由 $ {x}^{2}-2x-3\geqslant 0 $ 得 $ x\leqslant -1 $ 或 $ x\geqslant 3 $ ;
由 $ {x}^{2}-2x-3 < 5 $ 得 $ -2 < x < 4 $ .
$ \therefore -2 < x\leqslant -1 $ 或 $ 3\leqslant x < 4 $ .
$ \therefore $ 原不等式的解集为 $ {x|-2 < x\leqslant -1 $ 或 $ 3\leqslant x < 4} $ .
4.关于 $ x $ 的不等式 $ {x}^{2}-(a+\dfrac{1}{a})x+1 < 0(a > 0) $ 恰有一个整数解,则实数 $ a $ 的取值范围是( )
A. $ {a|\dfrac{1}{2} < a < 1或1 < a < 2} $
B. $ {a|\dfrac{1}{2}\leqslant a < 1或1 < a\leqslant 2} $
C. $ {a|\dfrac{1}{2}\leqslant a\leqslant 2} $
D. $ {a|0 < a < 1 $ 或 $ 1 < a < 2} $
答案:B
解析: $ {x}^{2}-(a+\dfrac{1}{a})x+1 < 0 $ ,即 $ (x-a)\cdot (x-\dfrac{1}{a}) < 0 $ ,
令 $ (x-a)(x-\dfrac{1}{a})=0 $ ,解得 $ x=a $ 或 $ x=\dfrac{1}{a} $ ,且 $ a > 0 $ ,
若 $ a > 1 > \dfrac{1}{a} > 0 $ ,则不等式的解集为 $ {x|\dfrac{1}{a} < x < a} $ ,由题意可得 $ 1 < a\leqslant 2 $ ;
若 $ a=1 $ ,则不等式的解集为 $ \mathrm{⌀} $ ,不合题意;
若 $ 0 < a < 1 < \dfrac{1}{a} $ ,则不等式的解集为 $ {x|\dfrac{1}{a} < x < a} $ ,由题意可得 $ 1 < \dfrac{1}{a}\leqslant 2 $ ,解得 $ \dfrac{1}{2}\leqslant a < 1 $ .
综上所述,实数 $ a $ 的取值范围是 $ {a|\dfrac{1}{2}\leqslant a < 1 $ 或 $ 1 < a\leqslant 2} $ .故选 $ \mathrm{B} $ .
5.关于 $ x $ 的不等式 $ x[x-(a+1)] < 0 $ 的解集是 $ {x|-1\leqslant x\leqslant 1} $ 的子集,则实数 $ a $ 的取值范围是( )
A. $ {a|0\leqslant a\leqslant 2} $
B. $ {a|-2\leqslant a < -1 $ 或 $ -1 < a\leqslant 0} $
C. $ {a|0\leqslant a < 1 $ 或 $ 1 < a\leqslant 2} $
D. $ {a|-2\leqslant a\leqslant 0} $
答案:D
解析:当 $ a+1=0 $ ,即 $ a=-1 $ 时, $ {x}^{2} < 0 $ 的解集为 $ \mathrm{⌀} $ , $ \mathrm{⌀}\subseteq {x|-1\leqslant x\leqslant 1} $ ,符合条件.
当 $ a+1 > 0 $ ,即 $ a > -1 $ 时,不等式 $ x[x-(a+1)] < 0 $ 的解集为 $ {x|0 < x < a+1} $ ,
所以 $ {x\left|0 < x < a+1}\subseteq {x\right|-1\leqslant x\leqslant 1} $ ,所以 $ \begin{cases}a > -1,\\ a+1\leqslant 1,\end{cases} $ 解得 $ -1 < a\leqslant 0 $ .
当 $ a+1 < 0 $ 时,即 $ a < -1 $ ,不等式 $ x[x-(a+1)] < 0 $ 的解集为 $ {x|a+1 < x < 0} $ ,
所以 $ {x\left|a+1 < x < 0}\subseteq {x\right|-1\leqslant x\leqslant 1} $ ,所以 $ \begin{cases}a < -1,\\ a+1\geqslant -1,\end{cases} $ 解得 $ -2\leqslant a < -1 $ .
综上, $ -2\leqslant a\leqslant 0 $ .故选 $ \mathrm{D} $ .
6.已知关于 $ x $ 的不等式 $ a{x}^{2}+bx+3 > 0 $ ,关于此不等式的解集有下列结论,其中正确的是( )(多选)
A.不等式的解集可以是 $ {x|x > 3} $
B.不等式的解集可以是 $ \boldsymbol{R} $
C.不等式的解集可以是 $ \mathrm{⌀} $
D.不等式的解集可以是 $ {x|-1 < x < 3} $
答案:BD
解析:选项 $ \mathrm{A} $ ,假设结论成立,则 $ \begin{cases}a=0,\\ 3b+3=0,\\ b > 0,\end{cases} $ 无解,故选项 $ \mathrm{A} $ 错误;
选项 $ \mathrm{B} $ ,当 $ a=1 $ , $ b=0 $ 时,不等式 $ {x}^{2}+3 > 0 $ 恒成立,则解集是 $ \boldsymbol{R} $ ,故选项 $ \mathrm{B} $ 正确;
选项 $ \mathrm{C} $ ,当 $ x=0 $ 时, $ a{x}^{2}+bx+3=3 > 0 $ ,则解集不可能为 $ \mathrm{⌀} $ ,故选项 $ \mathrm{C} $ 错误;
选项 $ \mathrm{D} $ ,假设结论成立,则 $ \begin{cases}a < 0,\\ a-b+3=0,\\ 9a+3b+3=0,\end{cases} $
解得 $ \begin{cases}a=-1,\\ b=2,\end{cases} $ 符合题意,故选项 $ \mathrm{D} $ 正确.故选 $ \mathrm{B}\mathrm{D} $ .
7.求关于 $ x $ 的不等式 $ a{x}^{2}+(2a-1)x-2 < 0 $ 的解集.
答案:【解】原不等式即为 $ (ax-1)(x+2) < 0 $ .
①当 $ a=0 $ 时, $ -x-2 < 0 $ ,解得 $ x > -2 $ ,故不等式的解集为 $ {x|x > -2} $ ;
②当 $ a > 0 $ 时, $ \dfrac{1}{a} > -2 $ ,解原不等式可得 $ -2 < x < \dfrac{1}{a} $ ,此时原不等式的解集为 $ {x|-2 < x < \dfrac{1}{a}} $ ;
③当 $ -\dfrac{1}{2} < a < 0 $ 时, $ \dfrac{1}{a} < -2 $ ,解原不等式可得 $ x < \dfrac{1}{a} $ 或 $ x > -2 $ ,此时原不等式的解集为 $ {x|x < \dfrac{1}{a} $ 或 $ x > -2} $ ;
④当 $ a=-\dfrac{1}{2} $ 时,原不等式即为 $ -\dfrac{1}{2}(x+2)^{2} < 0 $ ,解得 $ x\ne -2 $ ,此时原不等式的解集为 $ {x|x\ne -2} $ ;
⑤当 $ a < -\dfrac{1}{2} $ 时, $ \dfrac{1}{a} > -2 $ ,解原不等式可得 $ x < -2 $ 或 $ x > \dfrac{1}{a} $ ,此时原不等式的解集为 $ {x|x < -2或x > \dfrac{1}{a}} $ .
综上所述,当 $ a < -\dfrac{1}{2} $ 时,原不等式的解集为 $ {x|x < -2或x > \dfrac{1}{a}} $ ;
当 $ a=-\dfrac{1}{2} $ 时,原不等式的解集为 $ {x|x\ne -2} $ ;
当 $ -\dfrac{1}{2} < a < 0 $ 时,原不等式的解集为 $ {x|x < \dfrac{1}{a} $ 或 $ x > -2} $ ;
当 $ a=0 $ 时,原不等式的解集为 $ {x|x > -2} $ ;
当 $ a > 0 $ 时,原不等式的解集为 $ {x|-2 < x < \dfrac{1}{a}} $ .
解析:
8.若关于 $ x $ 的一元二次不等式 $ a{x}^{2}+bx+c > 0 $ 的解集为 $ {x|x < \dfrac{1}{3} $ 或 $ x > \dfrac{1}{2}} $ ,则关于 $ x $ 的不等式 $ c{x}^{2}+bx+a < 0 $ 的解集是( )
A. $ {x|-3 < x < -2} $
B. $ {x|2 < x < 3} $
C. $ {x|x > 3 $ 或 $ x < 2} $
D. $ {x|x > -2 $ 或 $ x < -3} $
答案:B
解析:因为关于 $ x $ 的一元二次不等式 $ a{x}^{2}+bx+c > 0 $ 的解集为 $ {x|x < \dfrac{1}{3} $ 或 $ x > \dfrac{1}{2}} $ ,所以 $ \dfrac{1}{2} $ , $ \dfrac{1}{3} $ 为关于 $ x $ 的一元二次方程 $ a{x}^{2}+bx+c=0 $ 的两根且 $ a > 0 $ ,
所以 $ \begin{cases}\dfrac{1}{2}+\dfrac{1}{3}=-\dfrac{b}{a},\\ \dfrac{1}{2}×\dfrac{1}{3}=\dfrac{c}{a},\end{cases} $
所以 $ b=-\dfrac{5}{6}a $ , $ c=\dfrac{1}{6}a $ ,则不等式 $ c{x}^{2}+bx+a < 0 $ ,即 $ \dfrac{1}{6}a{x}^{2}-\dfrac{5}{6}ax+a < 0 $ .因为 $ a > 0 $ ,所以 $ {x}^{2}-5x+6 < 0 $ ,即 $ (x-3)(x-2) < 0 $ ,解得 $ 2 < x < 3 $ ,所以不等式 $ c{x}^{2}+bx+a < 0 $ 的解集是 $ {x|2 < x < 3} $ .故选 $ \mathrm{B} $ .
9.(多选)已知关于 $ x $ 的一元二次不等式 $ a{x}^{2}+bx+c\geqslant 0 $ 的解集为 $ {x|x\leqslant -2 $ 或 $ x\geqslant 1} $ ,则( )(多选)
A. $ b > 0 $ 且 $ c < 0 $
B. $ 4a+2b+c=0 $
C.不等式 $ bx+c > 0 $ 的解集为 $ {x|x > 2} $
D.不等式 $ c{x}^{2}-bx+a < 0 $ 的解集为 $ {x|-1 < x < \dfrac{1}{2}} $
答案:AC
解析:依题意可得方程 $ a{x}^{2}+bx+c=0 $ 的根为 $ x=-2 $ 或 $ x=1 $ ,且 $ a > 0 $ ,
所以 $ \begin{cases}-2+1=-\dfrac{b}{a},\\ -2×1=\dfrac{c}{a},\end{cases} $ 即 $ b=a $ , $ c=-2a $ .
对于 $ \mathrm{A} $ ,由 $ a > 0 $ 可得 $ b=a > 0 $ , $ c=-2a < 0 $ ,故 $ \mathrm{A} $ 正确;
对于 $ \mathrm{B} $ ,易知 $ 4a+2b+c=4a > 0 $ ,故 $ \mathrm{B} $ 错误;
对于 $ \mathrm{C} $ ,不等式 $ bx+c > 0 $ ,即 $ ax-2a > 0 $ ,可得 $ x > 2 $ ,所以不等式 $ bx+c > 0 $ 的解集为 $ {x|x > 2} $ ,故 $ \mathrm{C} $ 正确;
对于 $ \mathrm{D} $ ,不等式 $ c{x}^{2}-bx+a < 0 $ ,即 $ -2a{x}^{2}-ax+a < 0 $ ,即 $ 2{x}^{2}+x-1 > 0 $ ,所以 $ (2x-1)(x+1) > 0 $ ,解得 $ x > \dfrac{1}{2} $ 或 $ x < -1 $ ,即不等式 $ c{x}^{2}-bx+a < 0 $ 的解集为 $ {x|x < -1或x > \dfrac{1}{2}} $ ,故 $ \mathrm{D} $ 错误.故选 $ \mathrm{A}\mathrm{C} $ .
10.若关于 $ x $ 的不等式 $ ax-b > 0 $ 的解集为 $ {x|x > 1} $ ,则关于 $ x $ 的不等式 $ \dfrac{ax+b}{x-2} > 0 $ 的解集为( )
A. $ {x|x < -2 $ 或 $ x > 1} $
B. $ {x|1 < x < 2} $
C. $ {x|x < -1 $ 或 $ x > 2} $
D. $ {x|-2 < x < -1} $
答案:C
解析:因为关于 $ x $ 的不等式 $ ax-b > 0 $ 的解集为 $ {x|x > 1} $ ,所以 $ a=b > 0 $ ,所以不等式 $ \dfrac{ax+b}{x-2} > 0 $ 等价于 $ \dfrac{x+1}{x-2} > 0 $ ,即 $ (x+1)(x-2) > 0 $ ,解得 $ x < -1 $ 或 $ x > 2 $ .所以关于 $ x $ 的不等式 $ \dfrac{ax+b}{x-2} > 0 $ 的解集为 $ {x|x < -1 $ 或 $ x > 2} $ .故选 $ \mathrm{C} $ .
11.若关于 $ x $ 的不等式 $ {x}^{2}+px+q < 0 $ 的解集是 $ {x|-1 < x < 2} $ ,则关于 $ x $ 的不等式 $ \dfrac{{x}^{2}+px-12}{x+q} > 0 $ 的解集是( )
A. $ {x|-3 < x < -2 $ 或 $ x > 4} $
B. $ {x|-3 < x < 2 $ 或 $ x > 4} $
C. $ {x|-3 < x < 0 $ 或 $ 2 < x < 4} $
D. $ {x|x < -2 $ 或 $ 3 < x < 4} $
答案:B
解析:由题意可得, $ {x}^{2}+px+q=(x+1)(x-2)={x}^{2}-x-2 $ ,即 $ p=-1 $ , $ q=-2 $ ,
则有 $ \dfrac{{x}^{2}+px-12}{x+q}=\dfrac{{x}^{2}-x-12}{x-2} > 0 $ ,即 $ ({x}^{2}-x-12)(x-2)=(x+3)(x-4)(x-2) > 0 $ ,解得 $ -3 < x < 2 $ 或 $ x > 4 $ ,即解集为 $ {x|-3 < x < 2 $ 或 $ x > 4} $ .故选 $ \mathrm{B} $ .
12.不等式 $ \dfrac{ (x+1)^{2} (5-x ) (x+2)^{3}}{ (x-1)^{5}}\geqslant 0 $ 的解集为 .
答案: $ {x|x\leqslant -2 $ 或 $ x=-1 $ 或 $ 1 < x\leqslant 5} $
解析:因为 $ \dfrac{{\left(x+1 \right) ^ {2}} (5-x ) (x+2)^{3}}{{\left(x-1 \right) ^ {5}}}\geqslant 0 $ ,
所以 $ \begin{cases}{\left(x+1 \right) ^ {2}} (5-x ) (x+2)^{3} (x-1)^{5}\geqslant 0,\\ (x-1)^{5}\ne 0,\end{cases} $
即 $ \begin{cases}{\left(x+1 \right) ^ {2}} (x-5 ) (x+2)^{3} (x-1)^{5}\leqslant 0,\\ (x-1)^{5}\ne 0.\end{cases} $
令 $ (x+1)^{2} (x-5 ) (x+2)^{3} (x-1)^{5}=0 $ ,解得 $ {x}_{1}={x}_{2}={x}_{3}=-2 $ , $ {x}_{4}={x}_{5}=-1 $ , $ {x}_{6}={x}_{7}={x}_{8}={x}_{9}={x}_{10}=1 $ , $ {x}_{11}=5 $ ,
采用“穿针引线法”,如图所示,
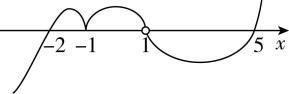
由图可得不等式的解集为 $ {x|x\leqslant -2 $ 或 $ x=-1 $ 或 $ 1 < x\leqslant 5} $ .
13.已知命题 $ p:\forall x\in \boldsymbol{R} $ , $ a{x}^{2}+2x+3 > 0 $ 为真命题,则实数 $ a $ 的取值范围是( )
A. $ {a|0 < a\leqslant \dfrac{1}{2}} $
B. $ {a|0 < a < \dfrac{1}{3}} $
C. $ {a|a\geqslant \dfrac{1}{3}} $
D. $ {a|a > \dfrac{1}{3}} $
答案:D
解析:因为命题 $ p:\forall x\in \boldsymbol{R} $ , $ a{x}^{2}+2x+3 > 0 $ 为真命题,所以不等式 $ a{x}^{2}+2x+3 > 0 $ 的解集为 $ \boldsymbol{R} $ .
若 $ a=0 $ ,则不等式 $ a{x}^{2}+2x+3 > 0 $ 可化为 $ 2x+3 > 0 $ ,解得 $ x > -\dfrac{3}{2} $ ,不等式的解集不是 $ \boldsymbol{R} $ ;
若 $ a\ne 0 $ ,则根据一元二次不等式解集的形式可知 $ \begin{cases}a > 0,\\ \mathrm{\Delta }={2}^{2}-12a < 0,\end{cases} $ 解得 $ a > \dfrac{1}{3} $ .
综上可知, $ a > \dfrac{1}{3} $ ,故选 $ \mathrm{D} $ .
14.若关于 $ x $ 的不等式 $ {x}^{2}-(m+1)x+9\leqslant 0 $ 在集合 $ {x|1\leqslant x\leqslant 4} $ 上有解,则实数 $ m $ 的最小值为( )
A.9
B.5
C.6
D. $ \dfrac{21}{4} $
答案:B
解析:因为不等式 $ {x}^{2}-(m+1)x+9\leqslant 0 $ 在集合 $ {x|1\leqslant x\leqslant 4} $ 上有解,所以 $ m+1\geqslant x+\dfrac{9}{x} $ 在集合 $ {x|1\leqslant x\leqslant 4} $ 上有解,所以 $ m+1\geqslant {(x+\dfrac{9}{x})}_{ \min }(x\in {x|1\leqslant x\leqslant 4}) $ .
又因为 $ x+\dfrac{9}{x}\geqslant 2\sqrt{x\cdot \dfrac{9}{x}}=6 $ ,当且仅当 $ x=\dfrac{9}{x} $ ,即 $ x=3 $ 时取等号,
所以 $ m+1\geqslant 6 $ ,所以 $ m\geqslant 5 $ ,即实数 $ m $ 的最小值为5,故选 $ \mathrm{B} $ .
15.(多选)为配制一种药液,进行了两次稀释,先在体积为 $ V $ 的桶中盛满纯药液,第一次将桶中药液倒出5升后用水补满,搅拌均匀,第二次倒出3升后用水补满,若在第二次稀释后桶中药液含量不超过容积的 $ 75\mathrm{\%} $ ,则 $ V $ 的可能取值为( )(多选)
A.4
B.40
C.8
D.28
答案:CD
解析:第一次稀释后,药液浓度为 $ \dfrac{V-5}{V} $ ,
第二次稀释后,药液浓度为 $ \dfrac{V-5-\dfrac{V-5}{V}×3}{V}=\dfrac{V+\dfrac{15}{V}-8}{V} $ ,
依题意有 $ \dfrac{V+\dfrac{15}{V}-8}{V}\leqslant 75\mathrm{\%} $ ,即 $ {V}^{2}-32V+60\leqslant 0 $ ,解得 $ 2\leqslant V\leqslant 30 $ ,
又 $ V-5\geqslant 0 $ ,即 $ V\geqslant 5 $ ,所以 $ 5\leqslant V\leqslant 30 $ .故选 $ \mathrm{C}\mathrm{D} $ .
16.某礼服租赁公司共有300套礼服供租赁,若每套礼服每天的租价为200元,则所有礼服均被租出;若将每套礼服每天的租价在200元的基础上提高 $ 10x $ 元 $ (1\leqslant x\leqslant 20,x\in \boldsymbol{Z}) $ ,则被租出的礼服会减少 $ 10x $ 套.若要使该礼服租赁公司每天租赁礼服的收入超过6.24万元,则该礼服租赁公司每套礼服每天的租价应定为( )
A.220元
B.240元
C.250元
D.280元
答案:C
解析:依题意,每天有 $ (300-10x) $ 套礼服被租出,
该礼服租赁公司每天租赁礼服的收入为
$ (300-10x)\cdot (200+10x)=-100{x}^{2}+1000x+60000 $ (元).
因为要使该礼服租赁公司每天租赁礼服的收入超过6.24万元,
所以 $ -100{x}^{2}+1000x+60000 > 62400 $ ,
即 $ {x}^{2}-10x+24 < 0 $ ,解得 $ 4 < x < 6 $ .因为 $ 1\leqslant x\leqslant 20 $ 且 $ x\in \boldsymbol{Z} $ ,所以 $ x=5 $ ,
即该礼服租赁公司每套礼服每天的租价应定为250元.
故选 $ \mathrm{C} $ .
17.若集合 $ A={x|a{x}^{2}-ax+1 < 0}=\mathrm{⌀} $ ,则实数 $ a $ 的取值范围是 .
解析:①若 $ a=0 $ ,则 $ 1 < 0 $ 不成立,此时解集为空集;
②若 $ a\ne 0 $ ,则 $ \begin{cases}\mathrm{\Delta }={a}^{2}-4a\leqslant 0,\\ a > 0,\end{cases} $ 解得 $ 0 < a\leqslant 4 $ .
综上知 $ 0\leqslant a\leqslant 4 $ .
18.若不等式 $ m{x}^{2}-4mx+3\ne 0 $ 对任意实数 $ x $ 均成立,则实数 $ m $ 的取值范围是 .
答案: $ {m|0\leqslant m < \dfrac{3}{4}} $
解析:①当 $ m=0 $ 时, $ 3\ne 0 $ 恒成立,满足条件.
②当 $ m\ne 0 $ 时,则 $ \mathrm{\Delta }=16{m}^{2}-12m < 0 $ ,解得 $ 0 < m < \dfrac{3}{4} $ .
综上,实数 $ m $ 的取值范围是 $ {m|0\leqslant m < \dfrac{3}{4}} $ .
19.解不等式: $ ({x}^{2}-4x+4)({x}^{2}-4x+3)\geqslant 0 $ .
解析:等式可化为 $ \begin{cases}x-2\ne 0,\\ \left(x-1\right)\left(x-3\right)\geqslant 0\end{cases} $ 或 $ x-2=0 $ ,解得 $ x\geqslant 3 $ 或 $ x\leqslant 1 $ 或 $ x=2 $ .
所以原不等式的解集为 $ {x|x\geqslant 3 $ 或 $ x\leqslant 1 $ 或 $ x=2} $ .
20.解不等式: $ \dfrac{x-1}{x+2}\leqslant 0 $ .
解析:原不等式可化为 $ \begin{cases}\left(x-1\right)\left(x+2\right)\leqslant 0,\\ x\ne -2,\end{cases} $
解得 $ -2 < x\leqslant 1 $ ,所以原不等式的解集为 $ {x|-2 < x\leqslant 1} $ .
二、刷能力
1.已知集合 $ M={x|\sqrt{x+1}\geqslant 0} $ , $ N={x|{x}^{2}+x-2 < 0} $ ,则 $ M\cap N= $ ( )
A. $ {x|x\geqslant -1} $
B. $ {x|x < 1} $
C. $ {x|-1 < x < 1} $
D. $ {x|-1\leqslant x < 1} $
答案:D
解析: $ \because M={x|x\geqslant -1} $ , $ N={x|(x+2)(x-1) < 0}={x|-2 < x < 1} $ ,
$ \therefore M\cap N={x|-1\leqslant x < 1} $ .
故选 $ \mathrm{D} $ .
2.“ $ \dfrac{x-2}{x+1}\geqslant 0 $ ”是“ $ |2x-1|\geqslant 3 $ ”的( )
A.充分不必要条件
B.必要不充分条件
C.充要条件
D.既不充分也不必要条件
答案:A
解析:由 $ \dfrac{x-2}{x+1}\geqslant 0⇒(x-2)(x+1)\geqslant 0 $ 且 $ x+1\ne 0 $ ,解得 $ x\geqslant 2 $ 或 $ x < -1 $ ,记不等式的解对应集合 $ A={x|x\geqslant 2 $ 或 $ x < -1} $ ,由 $ |2x-1|\geqslant 3⇒2x-1\geqslant 3 $ 或 $ 2x-1\leqslant -3 $ ,解得 $ x\geqslant 2 $ 或 $ x\leqslant -1 $ ,记不等式的解对应集合 $ B={x|x\geqslant 2 $ 或 $ x\leqslant -1} $ ,显然 $ A $ 是 $ B $ 的真子集,所以“ $ \dfrac{x-2}{x+1}\geqslant 0 $ ”是“ $ |2x-1|\geqslant 3 $ ”的充分不必要条件.故选 $ \mathrm{A} $ .
3.在 $ \boldsymbol{R} $ 上定义运算 $ \otimes :a\otimes b=ab+2a+b $ ,则满足 $ x\otimes (x-2) < 0 $ 的实数 $ x $ 的取值范围为( )
A. $ {x|0 < x < 2} $
B. $ {x|-2 < x < 1} $
C. $ {x|x < -2 $ 或 $ x > 1} $
D. $ {x|-1 < x < 2} $
答案:B
解析: $ \because x\otimes (x-2)=x(x-2)+2x+x-2 < 0 $ , $ \therefore {x}^{2}+x-2 < 0 $ ,即 $ (x-1)(x+2) < 0 $ ,解得 $ -2 < x < 1 $ .故选 $ \mathrm{B} $ .
4.若关于 $ x $ 的不等式 $ a{x}^{2}+2ax+3a-4 < 0 $ 对 $ x\in \boldsymbol{R} $ 恒成立,则 $ a $ 的取值集合为( )
A. $ {a|-2 < a < 0} $
B. $ {a|-2 < a\leqslant 0} $
C. $ {a|a < 0} $
D. $ {a|a\leqslant 0} $
答案:D
解析:当 $ a=0 $ 时,不等式 $ a{x}^{2}+2ax+3a-4 < 0 $ 化为 $ -4 < 0 $ ,对 $ x\in \boldsymbol{R} $ 恒成立;
当 $ a\ne 0 $ 时,要使得不等式 $ a{x}^{2}+2ax+3a-4 < 0 $ 对 $ x\in \boldsymbol{R} $ 恒成立,则 $ \begin{cases}a < 0,\\ \mathrm{\Delta }=4{a}^{2}-4a(3a-4) < 0,\end{cases} $ 解得 $ a < 0 $ .
综上, $ a $ 的取值集合为 $ {a|a\leqslant 0} $ .故选 $ \mathrm{D} $ .
5.已知关于 $ x $ 的不等式 $ {x}^{2}-(a+1)x+a < 0 $ 恰有四个整数解,则实数 $ a $ 的取值范围是( )
A. $ {a|5 < a\leqslant 6} $
B. $ {a|-4\leqslant a < -3} $
C. $ {a|-4\leqslant a < -3 $ 或 $ 5 < a\leqslant 6} $
D. $ {a|-4 < a\leqslant -3 $ 或 $ 5\leqslant a < 6} $
答案:C
解析:不等式 $ {x}^{2}-(a+1)x+a < 0 $ ,可化为 $ (x-a)(x-1) < 0 $ .
当 $ a=1 $ 时,不等式 $ {x}^{2}-(a+1)x+a < 0 $ 的解集为空集,不符合题意;
当 $ a > 1 $ 时,不等式 $ {x}^{2}-(a+1)x+a < 0 $ 的解集为 $ {x|1 < x < a} $ ,
要使不等式 $ {x}^{2}-(a+1)x+a < 0 $ 恰有四个整数解,则 $ 5 < a\leqslant 6 $ ;
当 $ a < 1 $ 时,不等式 $ {x}^{2}-(a+1)x+a < 0 $ 的解集为 $ {x|a < x < 1} $ ,
要使不等式 $ {x}^{2}-(a+1)x+a < 0 $ 恰有四个整数解,则 $ -4\leqslant a < -3 $ .
综上可得,实数 $ a $ 的取值范围是 $ {a|-4\leqslant a < -3 $ 或 $ 5 < a\leqslant 6} $ .故选 $ \mathrm{C} $ .
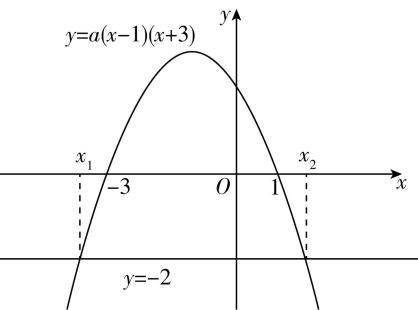
6.已知关于 $ x $ 的不等式 $ a(x-1)(x+3)+2 > 0 $ 的解集是 $ {x|{x}_{1} < x < {x}_{2}} $ ,其中 $ {x}_{1} < {x}_{2} $ ,则下列结论中正确的是( )(多选)
A. $ {x}_{1}+{x}_{2}+2=0 $
B. $ -3 < {x}_{1} < {x}_{2} < 1 $
C. $ |{x}_{1}-{x}_{2}| > 4 $
D. $ {x}_{1}{x}_{2}+3 < 0 $
答案:ACD
解析:由题设,不等式 $ a(x-1)\cdot (x+3)+2 > 0 $ ,即 $ a{x}^{2}+2ax-3a+2 > 0 $ 的解为 $ {x}_{1} < x < {x}_{2} $ , $ \therefore a < 0 $ ,则 $ \begin{cases}{x}_{1}+{x}_{2}=-2,\\ {x}_{1}{x}_{2}=\dfrac{2}{a}-3 < 0,\end{cases}\therefore {x}_{1}+{x}_{2}+2=0 $ , $ {x}_{1}{x}_{2}+3=\dfrac{2}{a} < 0 $ ,则 $ \mathrm{A} $ , $ \mathrm{D} $ 正确;
原不等式可化为 $ a(x-1)(x+3) > -2 $ ,令 $ y=a(x-1)(x+3) $ ,由题意可知函数图象开口向下,与 $ x $ 轴两交点的横坐标分别为 $ -3 $ 和1,与直线 $ y=-2 $ 两交点的横坐标分别为 $ {x}_{1} $ , $ {x}_{2} $ ,且 $ {x}_{1} < {x}_{2} $ ,作出大致图象如图所示, $ \therefore $ 由图知 $ {x}_{1} < -3 < 1 < {x}_{2} $ , $ |{x}_{1}-{x}_{2}| > 4 $ ,故 $ \mathrm{B} $ 错误, $ \mathrm{C} $ 正确.故选 $ \mathrm{A}\mathrm{C}\mathrm{D} $ .
7.(多选)已知关于 $ x $ 的不等式 $ a\leqslant \dfrac{3}{4}{x}^{2}-3x+4\leqslant b $ ,下列结论正确的是( )(多选)
A.当 $ a < b < 1 $ 时,不等式 $ a\leqslant \dfrac{3}{4}{x}^{2}-3x+4\leqslant b $ 的解集为 $ \mathrm{⌀} $
B.当 $ 1 < a < b $ 时,不等式 $ a\leqslant \dfrac{3}{4}{x}^{2}-3x+4\leqslant b $ 的解集为 $ {x|d\leqslant x\leqslant f} $ 的形式
C.当 $ a < b=1 $ 时,不等式 $ a\leqslant \dfrac{3}{4}{x}^{2}-3x+4\leqslant b $ 的解集为 $ {2} $
D.如果不等式 $ a\leqslant \dfrac{3}{4}{x}^{2}-3x+4\leqslant b $ 的解集恰好为 $ {x|a\leqslant x\leqslant b} $ ,那么 $ b-a=4 $
答案:ACD
解析:由 $ \dfrac{3}{4}{x}^{2}-3x+4\leqslant b $ ,得 $ 3{x}^{2}-12x+16-4b\leqslant 0 $ ,当 $ b < 1 $ 时, $ \mathrm{\Delta }=48(b-1) < 0 $ ,
从而不等式 $ a\leqslant \dfrac{3}{4}{x}^{2}-3x+4\leqslant b $ 的解集为 $ \mathrm{⌀} $ ,故 $ \mathrm{A} $ 正确.
在同一平面直角坐标系中作出函数 $ y=\dfrac{3}{4}{x}^{2}-3x+4=\dfrac{3}{4}{\left(x-2\right) ^ {2}}+1 $ 的图象及直线 $ y=a $ 和 $ y=b $ ,如图所示.
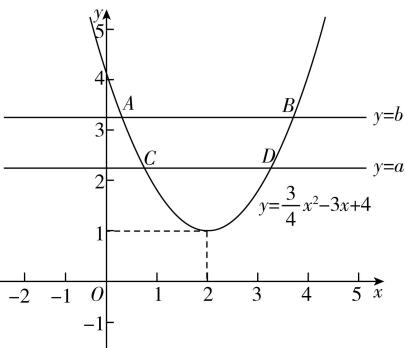
由图知,当 $ 1 < a < b $ 时,不等式 $ a\leqslant \dfrac{3}{4}{x}^{2}-3x+4\leqslant b $ 的解集为 $ {x|{x}_{A}\leqslant x\leqslant {x}_{C}}\cup {x|{x}_{D}\leqslant x\leqslant {x}_{B}} $ 的形式,故 $ \mathrm{B} $ 错误.
当 $ a < b=1 $ 时,不等式 $ a\leqslant \dfrac{3}{4}{x}^{2}-3x+4\leqslant b $ 的解集为 $ {2} $ , $ \mathrm{C} $ 正确.
由不等式 $ a\leqslant \dfrac{3}{4}{x}^{2}-3x+4\leqslant b $ 的解集恰好为 $ {x|a\leqslant x\leqslant b} $ ,可知 $ a\leqslant {y}_{ \min } $ ,即 $ a\leqslant 1 $ ,且 $ x=a $ , $ x=b $ 时函数值均是 $ b $ ,得 $ \dfrac{3}{4}{b}^{2}-3b+4=b $ ,解得 $ b=\dfrac{4}{3} $ 或 $ b=4 $ ,当 $ b=\dfrac{4}{3} $ 时,由 $ \dfrac{3}{4}{a}^{2}-3a+4=b=\dfrac{4}{3} $ ,解得 $ a=\dfrac{4}{3} $ 或 $ a=\dfrac{8}{3} $ ,不满足 $ a\leqslant 1 $ ,不符合题意;
当 $ b=4 $ 时,由 $ \dfrac{3}{4}{a}^{2}-3a+4=b=4 $ ,解得 $ a=0 $ 或 $ a=4 $ ,只有 $ a=0 $ 满足 $ a\leqslant 1 $ ,所以 $ a=0 $ ,此时 $ b-a=4-0=4 $ ,故 $ \mathrm{D} $ 正确.故选 $ \mathrm{A}\mathrm{C}\mathrm{D} $ .
8.如图,某小区要建一个八边形的休闲场所,它的主体造型平面图是由两个周长均为 $ 24\mathrm{m} $ 的相同的矩形 $ ABCD $ 和 $ EFGH $ 构成的十字形地域.计划在正方形 $ MNPQ $ 上建一座花坛,造价为2 000元/ $ {\mathrm{m}}^{2} $ ;在四个相同的矩形(图中阴影部分)内铺上塑胶,造价为100元/ $ {\mathrm{m}}^{2} $ ;在四个空角(图中四个三角形)内铺上草坪,造价为400元/ $ {\mathrm{m}}^{2} $ .若要使总造价不高于24 000元,则正方形 $ MNPQ $ 周长的最小值为 $ \mathrm{m} $ .
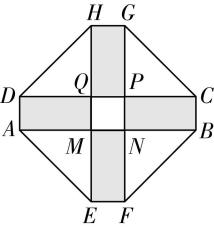
解析:设正方形 $ MNPQ $ 的边长为 $ a\mathrm{m} $ ,则矩形 $ EFNM $ 的长 $ NF $ ,宽 $ MN $ 分别为 $ \dfrac{24-4a}{4}=(6-a)\mathrm{m} $ , $ a\mathrm{m} $ ,所以 $ {S}_{正方形MNPQ}={a}^{2} $ , $ 4{S}_{矩形EFNM}=4a(6-a) $ , $ 4{S}_{△PGC}=4×\dfrac{1}{2}(6-a)^{2}=2(6-a)^{2} $ ,所以总造价 $ y=2000{a}^{2}+400a (6-a )+800 (6-a)^{2}\leqslant 24000 $ ,
且 $ 0 < a < 6 $ ,所以 $ 5{a}^{2}+a(6-a)+{2(6-a)}^{2}\leqslant 60 $ ,则 $ {a}^{2}-3a+2\leqslant 0 $ ,解得 $ 1\leqslant a\leqslant 2 $ ,
故 $ {a}_{ \min }=1 $ ,则正方形 $ MNPQ $ 周长的最小值为 $ 4\mathrm{m} $ .
9.已知 $ a > 0 $ ,关于 $ x $ 的不等式 $ {x}^{2}-ax+6\leqslant 0 $ 的解集中有且仅有3个整数 $ n-1 $ , $ n $ , $ n+1 $ ,则 $ n= $ ,实数 $ a $ 的取值范围为 .
答案:3; $ {a|\dfrac{11}{2}\leqslant a < \dfrac{31}{5}} $
解析:由题意, $ \mathrm{\Delta }={a}^{2}-24 > 0 $ ,即 $ a > 2\sqrt{6} $ .
设不等式的解集为 $ {x|{x}_{1}\leqslant x\leqslant {x}_{2}} $ ,则 $ {x}_{1}+{x}_{2}=a $ , $ {x}_{1}{x}_{2}=6 $ ,
则 $ {x}_{2}-{x}_{1}=\sqrt{{\left({x}_{1}+{x}_{2}\right) ^ {2}}-4{x}_{1}{x}_{2}}=\sqrt{{a}^{2}-24} $ .
因为不等式解集中有且仅有3个整数,所以 $ 2\leqslant {x}_{2}-{x}_{1} < 4 $ ,
即 $ 2\leqslant \sqrt{{a}^{2}-24} < 4 $ ,解得 $ 2\sqrt{7}\leqslant a < 2\sqrt{10} $ ,
所以 $ y={x}^{2}-ax+6 $ 的图象的对称轴 $ x=\dfrac{a}{2} $ 满足 $ \sqrt{7}\leqslant x=\dfrac{a}{2} < \sqrt{10} $ ,而 $ \sqrt{7} < 3 < \sqrt{10} $ ,即离对称轴最近的整数只有3,所以 $ n=3 $ ,所以三个整数解为2,3,4,
所以 $ \begin{cases}2\sqrt{7}\leqslant a < 2\sqrt{10},\\ 4-2a+6\leqslant 0,\\ 1-a+6 > 0,\\ 16-4a+6\leqslant 0,\\ 25-5a+6 > 0,\end{cases} $ 解得 $ \dfrac{11}{2}\leqslant a < \dfrac{31}{5} $ ,
即 $ a $ 的取值范围为 $ {a|\dfrac{11}{2}\leqslant a < \dfrac{31}{5}} $ .
10.求所有的实数 $ a $ ,使 $ |{x}^{2}+ax+2|\geqslant |x+1| $ 对任意 $ x\in \boldsymbol{R} $ 恒成立.
答案:【解】①若方程 $ {x}^{2}+ax+2=0 $ 有实数解 $ {x}_{0} $ ,则 $ 0=|{x}_{0}^{2}+a{x}_{0}+2|\geqslant |{x}_{0}+1| $ .此时 $ {x}_{0}=-1 $ ,则有 $ 1+a\cdot (-1)+2=0⇒a=3 $ ,则 $ |{x}^{2}+3x+2|\geqslant |x+1| $ ,又易知该不等式在 $ x=-2 $ 时不成立,故该情况不满足题意.
②若方程 $ {x}^{2}+ax+2=0 $ 不存在实数解,则 $ {x}^{2}+ax+2 > 0 $ 恒成立,此时 $ \mathrm{\Delta }={a}^{2}-8 < 0 $ ,解得 $ -2\sqrt{2} < a < 2\sqrt{2} $ ,则原不等式等价于 $ {x}^{2}+ax+2\geqslant x+1 $ 且 $ {x}^{2}+ax+2\geqslant -x-1 $ .
当 $ {x}^{2}+ax+2\geqslant x+1 $ 时,有 $ {x}^{2}+(a-1)x+1\geqslant 0 $ , $ \therefore {\mathrm{\Delta }}_{1}=(a-1)^{2}-4\leqslant 0 $ , $ \therefore -1\leqslant a < 2\sqrt{2} $ ;
当 $ {x}^{2}+ax+2\geqslant -x-1 $ 时,有 $ {x}^{2}+(a+1)x+3\geqslant 0 $ , $ \therefore {\mathrm{\Delta }}_{2}=(a+1)^{2}-12\leqslant 0 $ , $ \therefore -2\sqrt{2} < a\leqslant 2\sqrt{3}-1 $ .
综上所述,所求实数 $ a $ 的取值范围为 $ {a|-1\leqslant a\leqslant 2\sqrt{3}-1} $ .
解析:



