第二章素养检测
一、刷速度
1.已知 $ -1\leqslant a+b\leqslant 2 $ , $ -3\leqslant a-2b\leqslant 1 $ ,则 $ a-b $ 的最大值是( )
A.4
B. $ \dfrac{10}{3} $
C. $ \dfrac{8}{3} $
D. $ \dfrac{4}{3} $
答案:D
解析:因为 $ -3\leqslant a-2b\leqslant 1 $ ,所以 $ -6\leqslant 2(a-2b)\leqslant 2 $ .
因为 $ 3a-3b=(a+b)+2(a-2b) $ ,且 $ -1\leqslant a+b\leqslant 2 $ ,所以 $ -7\leqslant 3a-3b\leqslant 4 $ ,
所以 $ -\dfrac{7}{3}\leqslant a-b\leqslant \dfrac{4}{3} $ .故 $ a-b $ 的最大值为 $ \dfrac{4}{3} $ .故选 $ \mathrm{D} $ .
2.不等式 $ 4+3x-{x}^{2} < 0 $ 的解集为( )
A. $ {x|-1 < x < 4} $
B. $ {x|x < -1 $ 或 $ x > 4} $
C. $ {x|x < -4 $ 或 $ x > 1} $
D. $ {x|-4 < x < 1} $
答案:B
解析:不等式 $ 4+3x-{x}^{2} < 0 $ 可化为 $ {x}^{2}-3x-4 > 0 $ ,即 $ (x+1)(x-4) > 0 $ ,解得 $ x < -1 $ 或 $ x > 4 $ .故所求不等式的解集为 $ {x|x < -1 $ 或 $ x > 4} $ .故选 $ \mathrm{B} $ .
3.已知 $ a $ , $ b $ 是两个实数,且 $ a\ne b $ ,有如下三个式子: $ \mathrm{①}{a}^{5}+{b}^{5} > {a}^{3}{b}^{2}+{a}^{2}{b}^{3} $ , $ \mathrm{②}{a}^{2}+{b}^{2}\geqslant 2(a-b-1) $ , $ \mathrm{③}\dfrac{a}{b}+\dfrac{b}{a} > 2 $ .其中恒成立的有( )
A.0个
B.1个
C.2个
D.3个
答案:B
解析: $ \mathrm{①}{a}^{5}+{b}^{5}- ({a}^{3}{b}^{2}+{a}^{2}{b}^{3} )={a}^{3} ({a}^{2}-{b}^{2} )+{b}^{3} ({b}^{2}-{a}^{2} )= ({a}^{2}-{b}^{2} ) ({a}^{3}-{b}^{3} )= (a-b)^{2} (a+b ) ({a}^{2}+ab+{b}^{2} ) > 0 $ 不恒成立;
$ \mathrm{②} ({a}^{2}+{b}^{2} )-2 (a-b-1 )={a}^{2}-2a+{b}^{2}+2b+2={\left(a-1 \right) ^ {2}}+ (b+1)^{2}\geqslant 0 $ 恒成立;
③当 $ a=1 $ , $ b=-1 $ 时, $ \dfrac{a}{b}+\dfrac{b}{a}=-2 $ ,故 $ \dfrac{a}{b}+\dfrac{b}{a} > 2 $ 不恒成立.故选 $ \mathrm{B} $ .
4.已知不等式 $ a{x}^{2}-10x+6a < 0 $ 的解集为 $ {x|2 < x < 3} $ ,且不等式 $ ({m}^{2}-2m-3){x}^{2}+(m+1)x+a > 0 $ 对于任意的 $ x\in \boldsymbol{R} $ 恒成立,则实数 $ m $ 的取值范围为( )
A. $ {m|m < -1或m > \dfrac{25}{7}} $
B. $ {m|m\leqslant -1或m > \dfrac{25}{7}} $
C. $ {m|-1\leqslant m < \dfrac{25}{7}} $
D. $ {m|-1 < m < \dfrac{25}{7}} $
答案:B
解析:由题意得,一元二次方程 $ a{x}^{2}-10x+6a=0 $ 的两根分别为2,3,
由根与系数的关系,可得 $ \begin{cases}2+3=\dfrac{10}{a},\\ 2×3=6,\end{cases} $ 得 $ a=2 $ ,则不等式 $ ({m}^{2}-2m-3){x}^{2}+(m+1)x+a > 0 $ ,
即 $ ({m}^{2}-2m-3){x}^{2}+(m+1)x+2 > 0 $ 对于任意的 $ x\in \boldsymbol{R} $ 恒成立,
等价于 $ \begin{cases}{m}^{2}-2m-3=0,\\ m+1=0\end{cases} $
或 $ \begin{cases}{m}^{2}-2m-3 > 0,\\ (m+1)^{2}-4×2 ({m}^{2}-2m-3 ) < 0,\end{cases} $
解得 $ m\leqslant -1 $ 或 $ m > \dfrac{25}{7} $ ,则实数 $ m $ 的取值范围为 $ {m|m\leqslant -1或m > \dfrac{25}{7}} $ .故选 $ \mathrm{B} $ .
5.若两个正实数 $ x $ , $ y $ 满足 $ \dfrac{1}{x}+\dfrac{4}{y}=2 $ ,且不等式 $ x+\dfrac{y}{4} < {m}^{2}-m $ 有解,则实数 $ m $ 的取值范围是( )
A. $ {m|-1 < m < 2} $
B. $ {m|m < -2 $ 或 $ m > 1} $
C. $ {m|-2 < m < 1} $
D. $ {m|m < -1 $ 或 $ m > 2} $
答案:D
解析: $ x+\dfrac{y}{4}=\dfrac{1}{2}(x+\dfrac{y}{4})(\dfrac{1}{x}+\dfrac{4}{y})=\dfrac{1}{2}(1+1+\dfrac{y}{4x}+\dfrac{4x}{y})\geqslant \dfrac{1}{2}(1+1+2\sqrt{\dfrac{y}{4x}\cdot \dfrac{4x}{y}})=2 $ ,当且仅当 $ x=1 $ , $ y=4 $ 时等号成立.要使得不等式 $ x+\dfrac{y}{4} < {m}^{2}-m $ 有解,只需 $ {m}^{2}-m > 2 $ ,解得 $ m > 2 $ 或 $ m < -1 $ ,故选 $ \mathrm{D} $ .
6.已知集合 $ A={x|{x}^{2}+mx+n\leqslant 0} $ , $ B={x|1\leqslant x\leqslant 2} $ ,若 $ x\in A $ 是 $ x\in B $ 的必要条件,则 $ 3m+2n $ 的最大值为( )
A. $ -1 $
B. $ -3 $
C. $ -4 $
D. $ -5 $
答案:D
解析:因为 $ x\in A $ 是 $ x\in B $ 的必要条件,所以 $ B\subseteq A $ ,所以 $ \forall x\in {\mathrm{x}|1\leqslant x\leqslant 2} {\rm \mathit{,}} $ $ {x}^{2}+mx+n\leqslant 0 $ 恒成立.
所以 $ \begin{cases}1+m+n\leqslant 0,\\ 4+2m+n\leqslant 0,\end{cases} $ 即 $ \begin{cases}m+n\leqslant -1,\\ 2m+n\leqslant -4,\end{cases} $ 又 $ 3m+2n=(m+n)+(2m+n) $ ,
所以 $ 3m+2n\leqslant -5 $ ,当且仅当 $ m=-3 $ , $ n=2 $ 时取等号,所以 $ 3m+2n $ 的最大值为 $ -5 $ .故选 $ \mathrm{D} $ .
7.设实数 $ x $ , $ y $ 满足 $ {x}^{2}-3xy-4{y}^{2}=1 $ ,则 $ {x}^{2}+4{y}^{2} $ 的最小值为( )
A. $ \dfrac{2}{5} $
B. $ \dfrac{3}{5} $
C. $ \dfrac{4}{5} $
D.1
答案:C
解析:因为 $ {x}^{2}-3xy-4{y}^{2}=1 $ ,所以 $ (x-4y)(x+y)=1 $ ,
令 $ \begin{cases}x-4y=m,\\ x+y=n,\end{cases} $ 则 $ \begin{cases}x=\dfrac{m+4n}{5},\\ y=\dfrac{n-m}{5},\end{cases} $ 因为 $ mn=1 $ ,所以 $ {x}^{2}+4{y}^{2}={\left(\dfrac{m+4n}{5}\right) ^ {2}}+4{\left(\dfrac{n-m}{5}\right) ^ {2}}=\dfrac{{m}^{2}+8mn+16{n}^{2}}{25}+\dfrac{4{m}^{2}-8mn+4{n}^{2}}{25}=\dfrac{5{m}^{2}+20{n}^{2}}{25}=\dfrac{{m}^{2}+4{n}^{2}}{5}\geqslant \dfrac{4mn}{5}=\dfrac{4}{5} $ ,当且仅当 $ m=2n $ ,即 $ \begin{cases}m=\sqrt{2},\\ n=\dfrac{\sqrt{2}}{2}\end{cases} $ 或 $ \begin{cases}m=-\sqrt{2},\\ n=-\dfrac{\sqrt{2}}{2}\end{cases} $ 时等号成立,所以 $ {x}^{2}+4{y}^{2} $ 的最小值为 $ \dfrac{4}{5} $ .故选 $ \mathrm{C} $ .
8.记不等式 $ {x}^{2}+x-2 > 0 $ , $ {x}^{2}-ax+1\leqslant 0(a > 0) $ 的解集分别为 $ A $ , $ B $ , $ A\cap B $ 中有且只有两个正整数解,则实数 $ a $ 的取值范围为( )
A. $ {a|\dfrac{10}{3} < a < \dfrac{17}{4}} $
B. $ {a|\dfrac{10}{3}\leqslant a < \dfrac{17}{4}} $
C. $ {a|\dfrac{5}{2} < a < \dfrac{17}{4}} $
D. $ {a|\dfrac{5}{2}\leqslant a < \dfrac{17}{4}} $
答案:B
解析:由 $ {x}^{2}+x-2 > 0 $ 可得 $ x > 1 $ 或 $ x < -2 $ ,所以 $ A={x|x < -2 $ 或 $ x > 1} $ .
因为 $ A\cap B $ 中有且只有两个正整数解,所以 $ A\cap B\ne \mathrm{⌀} $ ,对于方程 $ {x}^{2}-ax+1=0(a > 0) $ ,判别式 $ \Delta ={a}^{2}-4\geqslant 0 $ ,所以方程的两根分别为 $ {x}_{1}=\dfrac{a-\sqrt{{a}^{2}-4}}{2} $ , $ {x}_{2}=\dfrac{a+\sqrt{{a}^{2}-4}}{2} $ ,
所以 $ B={x|\dfrac{a-\sqrt{{a}^{2}-4}}{2}\leqslant x\leqslant \dfrac{a+\sqrt{{a}^{2}-4}}{2}} $ .
因为 $ A\cap B $ 中有且只有两个正整数解,所以当 $ {x}_{1}=\dfrac{a-\sqrt{{a}^{2}-4}}{2} > 1 $ 时,解得 $ 0 < a < 2 $ ,此时 $ \Delta ={a}^{2}-4 < 0 $ , $ B=\mathrm{⌀} $ ,不符合题意;
当 $ \dfrac{a-\sqrt{{a}^{2}-4}}{2}\leqslant 1 $ 时,则 $ \begin{cases}\dfrac{a-\sqrt{{a}^{2}-4}}{2}\leqslant 1,\\ 3\leqslant \dfrac{a+\sqrt{{a}^{2}-4}}{2} < 4,\end{cases} $
即 $ \begin{cases}a-2\leqslant \sqrt{{a}^{2}-4},\\ 6-a\leqslant \sqrt{{a}^{2}-4} < 8-a,\end{cases} $ 解得 $ \begin{cases}a\geqslant 2,\\ a\geqslant \dfrac{10}{3},\\ a < \dfrac{17}{4},\end{cases} $
所以 $ \dfrac{10}{3}\leqslant a < \dfrac{17}{4} $ .
综上所述,实数 $ a $ 的取值范围为 $ \dfrac{10}{3}\leqslant a < \dfrac{17}{4} $ .故选 $ \mathrm{B} $ .
9.生活经验告诉我们, $ a $ 克糖水中有 $ b $ 克糖 $ (a > 0 $ , $ b > 0 $ ,且 $ a > b) $ ,若再添加 $ c $ 克糖 $ (c > 0) $ 后,糖水会更甜,于是得出一个不等式: $ \dfrac{b+c}{a+c} > \dfrac{b}{a} $ ,趣称之为“糖水不等式”.根据生活经验和不等式的性质判断下列命题一定正确的是( )(多选)
A.若 $ a > b > 0 $ , $ m > 0 $ ,则 $ \dfrac{b+m}{a+m} $ 与 $ \dfrac{b}{a} $ 的大小关系随 $ m $ 的变化而变化
B.若 $ b > a > 0 $ , $ m > 0 $ ,则 $ \dfrac{b}{a} > \dfrac{b+m}{a+m} $
C.若 $ a > b > 0 $ , $ c > d > 0 $ ,则 $ \dfrac{b+d}{a+d} < \dfrac{b+c}{a+c} $
D.若 $ a > 0 $ , $ b > 0 $ ,则一定有 $ \dfrac{a+b}{1+a+b} < \dfrac{a}{1+a}+\dfrac{b}{1+b} $
答案:BCD
解析:对于 $ \mathrm{A} $ , $ \because a > b > 0 $ , $ m > 0 $ , $ \therefore \dfrac{b+m}{a+m}-\dfrac{b}{a}=\dfrac{m(a-b)}{a(a+m)} > 0 $ , $ \therefore \dfrac{b+m}{a+m} > \dfrac{b}{a} $ ,故 $ \mathrm{A} $ 错误;
对于 $ \mathrm{B} $ , $ \because b > a > 0 $ , $ m > 0 $ , $ \therefore \dfrac{b+m}{a+m}-\dfrac{b}{a}=\dfrac{m(a-b)}{a(a+m)} < 0 $ , $ \therefore \dfrac{b}{a} > \dfrac{b+m}{a+m} $ ,故 $ \mathrm{B} $ 正确;
对于 $ \mathrm{C} $ , $ \because a > b > 0 $ , $ c > d > 0 $ , $ \therefore a-b > 0 $ , $ c-d > 0 $ ,
$ \therefore \dfrac{b+c}{a+c}-\dfrac{b+d}{a+d}=\dfrac{(b+c)(a+d)-(b+d)(a+c)}{(a+c)(a+d)}=\dfrac{(a-b)(c-d)}{(a+c)(a+d)} > 0 $ , $ \therefore \dfrac{b+d}{a+d} < \dfrac{b+c}{a+c} $ ,故 $ \mathrm{C} $ 正确;
对于 $ \mathrm{D} $ , $ \because 0 < 1+a < 1+a+b $ , $ 0 < 1+b < 1+a+b $ , $ \therefore \dfrac{a}{1+a} > \dfrac{a}{1+a+b} $ , $ \dfrac{b}{1+b} > \dfrac{b}{1+a+b} $ ,
$ \therefore \dfrac{a}{1+a}+\dfrac{b}{1+b} > \dfrac{a}{1+a+b}+\dfrac{b}{1+a+b}=\dfrac{a+b}{1+a+b} $ ,故 $ \mathrm{D} $ 正确.故选 $ \mathrm{B}\mathrm{C}\mathrm{D} $ .
10.已知关于 $ x $ 的一元二次不等式 $ a{x}^{2}+bx+c > 0 $ 的解集为 $ M $ ,则下列说法正确的是( )(多选)
A.若 $ M=\mathrm{⌀} $ ,则 $ a < 0 $ 且 $ {b}^{2}-4ac\leqslant 0 $
B.若 $ \dfrac{a}{a\prime }=\dfrac{b}{b\prime }=\dfrac{c}{c\prime } $ ,则关于 $ x $ 的不等式 $ a\prime {x}^{2}+b\prime x+c\prime > 0 $ 的解集也为 $ M $
C.若 $ M={x|-1 < x < 2} $ ,则关于 $ x $ 的不等式 $ a({x}^{2}+1)+b(x-1)+c < 2ax $ 的解集为 $ N={x|x < 0 $ 或 $ x > 3} $
D.若 $ M={x|x\ne {x}_{0} $ , $ {x}_{0} $ 为常数 $ } $ ,且 $ a < b $ ,则 $ \dfrac{a+3b+4c}{b-a} $ 的最小值为 $ 5+2\sqrt{5} $
答案:ACD
解析: $ \mathrm{A} $ 选项,若 $ M=\mathrm{⌀} $ ,即一元二次不等式 $ a{x}^{2}+bx+c > 0 $ 无解,
则一元二次不等式 $ a{x}^{2}+bx+c\leqslant 0 $ 恒成立, $ \therefore a < 0 $ 且 $ {b}^{2}-4ac\leqslant 0 $ ,故 $ \mathrm{A} $ 正确;
$ \mathrm{B} $ 选项,令 $ \dfrac{a}{a\prime }=\dfrac{b}{b\prime }=\dfrac{c}{c\prime }=t(t\ne 0) $ ,则 $ a\prime =\dfrac{a}{t} $ , $ b\prime =\dfrac{b}{t} $ , $ c\prime =\dfrac{c}{t} $ , $ \therefore a\prime {x}^{2}+b\prime x+c\prime > 0 $ 可化为 $ \dfrac{1}{t}(a{x}^{2}+bx+c) > 0 $ ,当 $ t < 0 $ 时, $ \dfrac{1}{t}(a{x}^{2}+bx+c) > 0 $ 可化为 $ a{x}^{2}+bx+c < 0 $ ,其解集不等于 $ M $ ,故 $ \mathrm{B} $ 错误;
$ \mathrm{C} $ 选项,若 $ M={x|-1 < x < 2} $ ,则 $ a < 0 $ ,且 $ -1 $ 和2是一元二次方程 $ a{x}^{2}+bx+c=0 $ 的两根,
$ \therefore -1+2=-\dfrac{b}{a} $ ,且 $ -1×2=\dfrac{c}{a} $ , $ \therefore b=-a $ , $ c=-2a $ , $ \therefore $ 关于 $ x $ 的不等式 $ a({x}^{2}+1)+b(x-1)+c < 2ax $ 可化为 $ a({x}^{2}+1)-a(x-1)-2a < 2ax $ ,可化为 $ a({x}^{2}-3x) < 0 $ , $ \because a < 0 $ , $ \therefore {x}^{2}-3x > 0 $ ,解得 $ x < 0 $ 或 $ x > 3 $ ,即不等式 $ a({x}^{2}+1)+b(x-1)+c < 2ax $ 的解集为 $ N={x|x < 0 $ 或 $ x > 3} $ ,故 $ \mathrm{C} $ 正确;
$ \mathrm{D} $ 选项, $ \because M={x|x\ne {x}_{0} $ , $ {x}_{0} $ 为常数 $ } $ , $ \therefore a > 0 $ 且 $ {b}^{2}-4ac=0 $ ,
$ \therefore \dfrac{a+3b+4c}{b-a}=\dfrac{a+3b+\dfrac{{b}^{2}}{a}}{b-a} $ ,
$ \because b > a > 0 $ , $ \therefore b-a > 0 $ ,令 $ b-a=t > 0 $ ,则 $ b=a+t $ ,
$ \therefore \dfrac{a+3b+\dfrac{{b}^{2}}{a}}{b-a}=\dfrac{a+3(a+t)+\dfrac{{\left(a+t\right) ^ {2}}}{a}}{t}=\dfrac{5a}{t}+\dfrac{t}{a}+5\geqslant 2\sqrt{\dfrac{5a}{t}\cdot \dfrac{t}{a}}+5=2\sqrt{5}+5 $ ,
当且仅当 $ t=\sqrt{5}a $ ,即 $ b=(1+\sqrt{5})a $ , $ c=\dfrac{(3+\sqrt{5})a}{2} $ ,且 $ a $ 为正数时,等号成立,所以 $ \dfrac{a+3b+4c}{b-a} $ 的最小值为 $ 5+2\sqrt{5} $ ,故 $ \mathrm{D} $ 正确.故选 $ \mathrm{A}\mathrm{C}\mathrm{D} $ .
11.已知 $ x > 0 $ , $ y > 0 $ ,且满足 $ xy+x+y=8 $ ,则下列说法正确的是( )(多选)
A. $ xy $ 的最大值为4
B. $ x+y $ 的最小值为2
C. $ 2x+y $ 的最小值为 $ 6\sqrt{2}-3 $
D. $ \dfrac{1}{x(y+1)}+\dfrac{1}{y} $ 的最小值为 $ \dfrac{1}{2} $
答案:ACD
解析:对于 $ \mathrm{A} $ ,由 $ xy+x+y=8 $ ,可得 $ x+y=8-xy\geqslant 2\sqrt{xy} $ ,即 $ xy+2\sqrt{xy}-8\leqslant 0 $ ,即 $ (\sqrt{xy}-2)(\sqrt{xy}+4)\leqslant 0 $ ,解得 $ 0 < \sqrt{xy}\leqslant 2 $ ,所以 $ xy\leqslant 4 $ ,当且仅当 $ x=y=2 $ 时,等号成立,故 $ \mathrm{A} $ 正确;
对于 $ \mathrm{B} $ ,由 $ xy+x+y=8 $ ,可得 $ 8-(x+y)=xy\leqslant {\left(\dfrac{x+y}{2}\right) ^ {2}} $ ,即 $ (x+y)^{2}+4 (x+y )-32\geqslant 0 $ ,
解得 $ x+y\geqslant 4 $ 或 $ x+y\leqslant -8 $ (舍),当且仅当 $ x=y=2 $ 时等号成立,因此 $ x+y $ 的最小值为4,故 $ \mathrm{B} $ 错误;
对于 $ \mathrm{C} $ ,易知 $ xy+x+y+1=9 $ ,即 $ (x+1)(y+1)=9 $ ,因此 $ 2x+y=2(x+1)+(y+1)-3\geqslant 2\sqrt{2(x+1)(y+1)}-3=6\sqrt{2}-3 $ ,
当且仅当 $ 2(x+1)=y+1 $ ,即 $ x=\dfrac{3\sqrt{2}}{2}-1 $ , $ y=3\sqrt{2}-1 $ 时等号成立,故 $ \mathrm{C} $ 正确;
对于 $ \mathrm{D} $ ,由 $ xy+x+y=8 $ ,易得 $ x(y+1)+y=8 $ ,所以 $ \dfrac{1}{x(y+1)}+\dfrac{1}{y}=\dfrac{1}{8}[\dfrac{1}{x(y+1)}+\dfrac{1}{y}]\cdot [x(y+1)+y]=\dfrac{1}{8}[1+\dfrac{y}{x(y+1)}+\dfrac{x(y+1)}{y}+1]\geqslant \dfrac{1}{8}[2+2\sqrt{\dfrac{y}{x(y+1)}\cdot \dfrac{x(y+1)}{y}}]=\dfrac{1}{2} $ ,
当且仅当 $ \dfrac{y}{x(y+1)}=\dfrac{x(y+1)}{y} $ ,即 $ x=\dfrac{4}{5} $ , $ y=4 $ 时,等号成立,故 $ \mathrm{D} $ 正确.故选 $ \mathrm{A}\mathrm{C}\mathrm{D} $ .
12.已知关于 $ x $ 的不等式 $ -{x}^{2}+4x\geqslant {a}^{2}-3a $ 在 $ \boldsymbol{R} $ 上有解,则实数 $ a $ 的取值范围是 .
答案: $ {a|-1\leqslant a\leqslant 4} $
解析:因为关于 $ x $ 的不等式 $ -{x}^{2}+4x\geqslant {a}^{2}-3a $ 在 $ \boldsymbol{R} $ 上有解, $ y=-{x}^{2}+4x=-{\left(x-2\right) ^ {2}}+4 $ 的最大值为4,所以 $ {a}^{2}-3a\leqslant 4 $ ,解得 $ -1\leqslant a\leqslant 4 $ .
13.将基本不等式 $ \sqrt{ab}\leqslant \dfrac{a+b}{2}(a > 0,b > 0) $ 推广可得正确结论 $ \sqrt[3]{abc}\leqslant \dfrac{a+b+c}{3}(a > 0,b > 0,c > 0) $ ,当且仅当 $ a=b=c $ 时,等号成立.利用此结论解决问题:已知一个矩形的周长为 $ 18\mathrm{c}\mathrm{m} $ ,将矩形围绕其一边旋转形成一个圆柱,当矩形的长是 $ \mathrm{c}\mathrm{m} $ 时,旋转形成的圆柱体积最大,其最大值是 $ {\mathrm{c}\mathrm{m}}^{3} $ .(答对一空给3分)
答案:6; $ 108\mathrm{\pi } $
解析:设矩形相邻两边的长分别为 $ x\mathrm{c}\mathrm{m} $ , $ y\mathrm{c}\mathrm{m} $ ,
则 $ x > 0 $ , $ y > 0 $ 且 $ x+y=\dfrac{18}{2}=9 $ ,
不妨设以长度为 $ x\mathrm{c}\mathrm{m} $ 的边进行旋转,
则圆柱的体积 $ V=\mathrm{\pi }\cdot x{y}^{2}=4\mathrm{\pi }\cdot x\cdot $ $ \dfrac{y}{2}\cdot \dfrac{y}{2}\leqslant 4\mathrm{\pi }\cdot {\left(\dfrac{\dfrac{1}{2}y+\dfrac{1}{2}y+x}{3}\right) ^ {3}}=4\mathrm{\pi }\cdot {\left(\dfrac{x+y}{3}\right) ^ {3}}=108\mathrm{\pi }({\mathrm{c}\mathrm{m}}^{3}) $ ,
当且仅当 $ \dfrac{1}{2}y=x $ ,即 $ x=3 $ , $ y=6 $ 时取等号,
所以当矩形的长是 $ 6\mathrm{c}\mathrm{m} $ 时,圆柱的体积最大,为 $ 108\mathrm{\pi }{\mathrm{c}\mathrm{m}}^{3} $ .
14.已知 $ a > 0 $ , $ b > 0 $ , $ c > 0 $ , $ {a}^{2}-ab+9{b}^{2}-5c=0 $ ,当 $ \dfrac{c}{ab} $ 取最小值时, $ {m}^{2}-3m\geqslant a+b-\dfrac{1}{3}c $ 恒成立,则实数 $ m $ 的取值范围是 .
答案: $ {m|m\leqslant -1 $ 或 $ m\geqslant 4} $
解析:因为 $ {a}^{2}-ab+9{b}^{2}-5c=0 $ ,所以 $ \dfrac{c}{ab}=\dfrac{1}{5}\cdot \dfrac{{a}^{2}-ab+9{b}^{2}}{ab}=\dfrac{1}{5}(\dfrac{a}{b}+\dfrac{9b}{a}-1)\geqslant \dfrac{1}{5}(2\sqrt{\dfrac{a}{b}\cdot \dfrac{9b}{a}}-1)=1 $ ,当且仅当 $ \dfrac{a}{b}=\dfrac{9b}{a} $ ,即 $ a=3b $ 时,等号成立.
当 $ a=3b $ 时, $ c=3{b}^{2} $ , $ a+b-\dfrac{1}{3}c=-{b}^{2}+4b=-(b-2)^{2}+4 $ ,所以当 $ b=2 $ 时, $ a+b-\dfrac{1}{3}c $ 取得最大值4.所以由 $ {m}^{2}-3m\geqslant a+b-\dfrac{1}{3}c $ 恒成立可得 $ {m}^{2}-3m\geqslant 4 $ ,解得 $ m\geqslant 4 $ 或 $ m\leqslant -1 $ ,故实数 $ m $ 的取值范围是 $ {m|m\leqslant -1 $ 或 $ m\geqslant 4} $ .
15.已知 $ a > b > 1 $ .
(1) 证明: $ \dfrac{a}{a-1} < \dfrac{b}{b-1} $ .
(2) 若 $ a+b=5 $ ,求 $ \dfrac{1}{a-1}+\dfrac{4}{b+1} $ 的最小值.
答案:(1) 【证明】因为 $ a > b > 1 $ ,所以 $ a-1 > 0 $ , $ b-1 > 0 $ , $ b-a < 0 $ ,
所以 $ \dfrac{a}{a-1}-\dfrac{b}{b-1}=\dfrac{a(b-1)-b(a-1)}{(a-1)(b-1)}=\dfrac{b-a}{(a-1)(b-1)} < 0 $ ,所以 $ \dfrac{a}{a-1} < \dfrac{b}{b-1} $ .
(2) 【解】因为 $ a > b > 1 $ ,所以 $ a-1 > 0 $ , $ b+1 > 0 $ ,又 $ a+b=5 $ ,
所以 $ \dfrac{1}{a-1}+\dfrac{4}{b+1}=\dfrac{1}{5}[(a-1)+(b+1)]\cdot (\dfrac{1}{a-1}+\dfrac{4}{b+1})=\dfrac{1}{5}[5+\dfrac{4(a-1)}{b+1}+\dfrac{b+1}{a-1}]\geqslant \dfrac{1}{5}×(5+2\sqrt{4})=\dfrac{9}{5} $ ,
当且仅当 $ \dfrac{4(a-1)}{b+1}=\dfrac{b+1}{a-1} $ ,即 $ a=\dfrac{8}{3} $ , $ b=\dfrac{7}{3} $ 时等号成立,
所以 $ \dfrac{1}{a-1}+\dfrac{4}{b+1} $ 的最小值是 $ \dfrac{9}{5} $ .
解析:
16.已知 $ {x}_{1} $ , $ {x}_{2} $ 是一元二次方程 $ (4{k}^{2}+1){x}^{2}-(4k+1)x+1=0 $ 的两个不相等的实数根.
(1) 若两根同号,求实数 $ k $ 的取值范围;
(2) 求使得 $ \dfrac{{x}_{1}}{{x}_{2}}+\dfrac{{x}_{2}}{{x}_{1}}+4 $ 的值为整数的整数 $ k $ 的值.
答案:(1) 【解】由题意得 $ \begin{cases}{x}_{1}{x}_{2}=\dfrac{1}{4{k}^{2}+1} > 0,\\ \mathrm{\Delta }={\left(4k+1\right) ^ {2}}-4(4{k}^{2}+1) > 0,\end{cases} $
解得 $ k > \dfrac{3}{8} $ ,所以实数 $ k $ 的取值范围为 $ {k|k > \dfrac{3}{8}} $ .
(2) 【解】由(1)知,当 $ k > \dfrac{3}{8} $ 时,方程有两个不相等的实数根,可知 $ {x}_{1}+{x}_{2}=\dfrac{4k+1}{4{k}^{2}+1} $ , $ {x}_{1}{x}_{2}=\dfrac{1}{4{k}^{2}+1} $ ,
于是 $ \dfrac{{x}_{1}}{{x}_{2}}+\dfrac{{x}_{2}}{{x}_{1}}+4=\dfrac{{\left({x}_{1}+{x}_{2}\right) ^ {2}}}{{x}_{1}{x}_{2}}+2=\dfrac{{\left(4k+1\right) ^ {2}}}{4{k}^{2}+1}+2=6+\dfrac{8k-3}{4{k}^{2}+1} $ ,
由 $ k > \dfrac{3}{8} $ ,可得 $ 8k-3 > 0 $ ,则 $ \dfrac{8k-3}{4{k}^{2}+1} > 0 $ ,即要使 $ \dfrac{8k-3}{4{k}^{2}+1} $ 的值为正整数,且 $ k $ 为整数,则 $ \dfrac{8k-3}{4{k}^{2}+1}\geqslant 1 $ ,
则有 $ 4{k}^{2}+1\leqslant 8k-3 $ ,化简得 $ (k-1)^{2}\leqslant 0 $ ,则 $ k=1 $ ,
令 $ k=1 $ ,此时 $ \dfrac{8k-3}{4{k}^{2}+1}=1 $ 为整数,则 $ k=1 $ 满足题意.
故使得 $ \dfrac{{x}_{1}}{{x}_{2}}+\dfrac{{x}_{2}}{{x}_{1}}+4 $ 的值为整数的整数 $ k $ 的值为1.
解析:
17.如图所示,将一矩形花坛 $ ABCD $ 扩建成一个更大的矩形花坛 $ AMPN $ ,要求 $ B $ 在 $ AM $ 上, $ D $ 在 $ AN $ 上,且对角线 $ MN $ 过点 $ C $ ,已知 $ AB=3 $ 米, $ AD=2 $ 米.
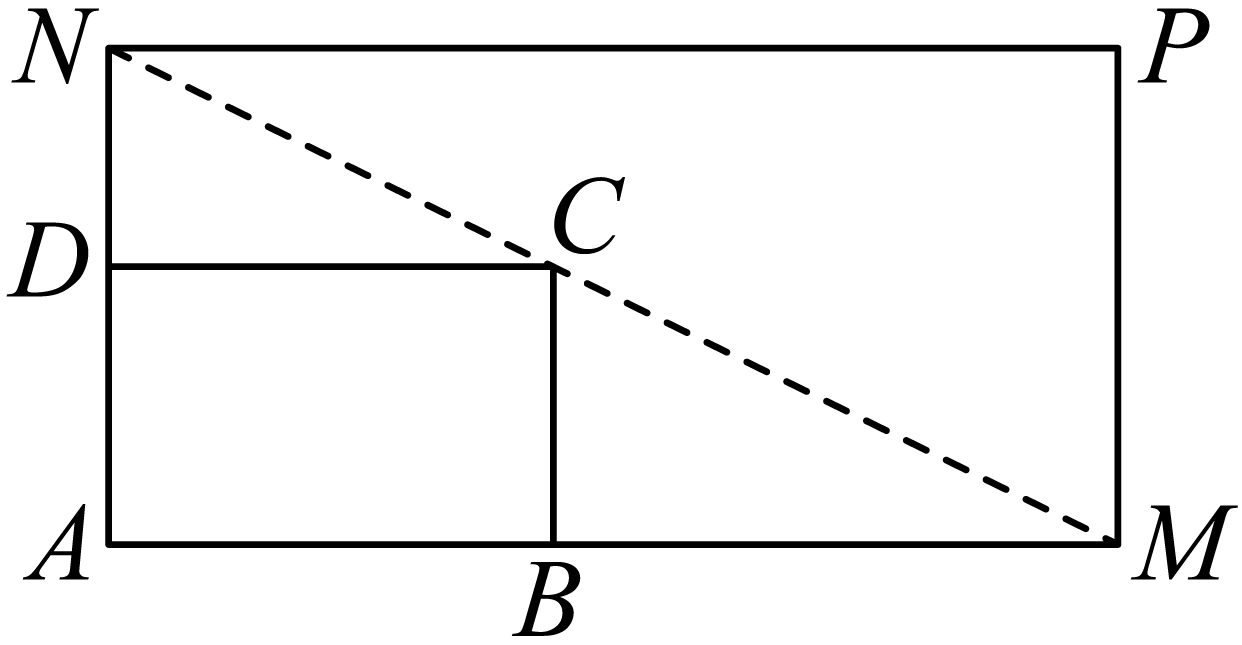
(1)要使矩形 $ AMPN $ 的面积大于32平方米,则 $ DN $ 的长应在什么范围?
(2)当 $ DN $ 的长为多少时,矩形花坛 $ AMPN $ 的面积最小?并求出最小值.
答案:(1) $ DN $ 的长应在 $ \left ( { 0,\dfrac { 2 } { 3 } } \right ) \cup \left ( { 6,+\infty } \right ) $
(2)当 $ DN $ 的长为 $ 2 $ 米,矩形花坛 $ AMPN $ 的面积最小,最小值 $ 24 $ 平方米
解析:(1)设 $ DN=x\left ( { x > 0 } \right ) ,BM=y\left ( { y > 0 } \right ) $ ,则由 $ \vartriangle NDC $ 与 $ \mathrm{ △ }NAM $ 相似得
$ \dfrac { x } { x+2 }=\dfrac { 3 } { 3+y } $ ,整理得 $ y=\dfrac { 6 } { x } $ ,
矩形 $ AMPN $ 的面积 $ S=AN\cdot AM=\left ( { x+2 } \right ) \left ( { 3+\dfrac { 6 } { x } } \right ) $ ,
即 $ S=3x+\dfrac { 12 } { x }+12 $ ,
当 $ S > 32 $ 时,得 $ 3x+\dfrac { 12 } { x }+12 > 32 $ ,整理得 $ \left ( { 3x-2 } \right ) \left ( { x-6 } \right ) > 0 $ ,
解得 $ x > 6 $ ,或 $ x < \dfrac { 2 } { 3 } $ ,又 $ x > 0 $ ,
所以 $ DN $ 的长应在 $ \left ( { 0,\dfrac { 2 } { 3 } } \right ) \cup \left ( { 6,+∞ } \right ) $ ;
(2) $ x > 0 $ 时, $ 3x+\dfrac { 12 } { x }\geqslant 2\sqrt { 3x\cdot \dfrac { 12 } { x } }=12 $ ,
当且仅当 $ 3x=\dfrac { 12 } { x } $ 即 $ x=2 $ 时等号成立,
所以 $ S\geqslant 12+12=24 $ ,
所以,当 $ DN $ 的长为 $ 2 $ 米,矩形花坛 $ AMPN $ 的面积最小,最小值 $ 24 $ 平方米.
18.已知函数 $ y=a{x}^{2}-(a+2)x+2 $ , $ a\in \boldsymbol{R} $ .
(1) 若 $ y < 3-2x $ 恒成立,求实数 $ a $ 的取值范围;
(2) 当 $ a > 0 $ 时,求不等式 $ y\geqslant 0 $ 的解集.
答案:(1) 【解】因为函数 $ y=a{x}^{2}-(a+2)x+2 $ ,
所以 $ y < 3-2x $ 恒成立等价于 $ a{x}^{2}-(a+2)\cdot x+2 < 3-2x $ 恒成立,
即 $ a{x}^{2}-ax-1 < 0 $ 恒成立.
当 $ a=0 $ 时, $ -1 < 0 $ 恒成立,满足题意;
当 $ a\ne 0 $ 时,要使 $ a{x}^{2}-ax-1 < 0 $ 恒成立,
则 $ \begin{cases}a < 0,\\ \mathrm{\Delta } < 0,\end{cases} $ 即 $ \begin{cases}a < 0,\\ {a}^{2}+4a < 0,\end{cases} $
解得 $ -4 < a < 0 $ .
综上,实数 $ a $ 的取值范围是 $ {a|-4 < a\leqslant 0} $ .
(2) 【解】由 $ y\geqslant 0 $ 得, $ a{x}^{2}-(a+2)x+2\geqslant 0 $ ,
即 $ (ax-2)(x-1)\geqslant 0 $ ,又因为 $ a > 0 $ ,
所以当 $ \dfrac{2}{a} > 1 $ ,即 $ 0 < a < 2 $ 时,
不等式的解集为 $ {x|x\leqslant 1 $ 或 $ x\geqslant \dfrac{2}{a}} $ ;
当 $ \dfrac{2}{a}=1 $ ,即 $ a=2 $ 时,
可得 $ (x-1)^{2}\geqslant 0 $ ,不等式的解集为 $ \boldsymbol{R} $ ;
当 $ \dfrac{2}{a} < 1 $ ,即 $ a > 2 $ 时,
不等式的解集为 $ {x|x\leqslant \dfrac{2}{a} $ 或 $ x\geqslant 1} $ .
综上,当 $ 0 < a < 2 $ 时,不等式的解集为 $ {x|x\leqslant 1或x\geqslant \dfrac{2}{a}} $ ;
当 $ a=2 $ 时,不等式的解集为 $ \boldsymbol{R} $ ;
当 $ a > 2 $ 时,不等式的解集为 $ {x|x\leqslant \dfrac{2}{a} $ 或 $ x\geqslant 1} $ .
解析:
19.(本小题满分17分)若实数 $ x $ , $ y $ , $ m $ 满足 $ (x-m)^{2} > (y-m)^{2} $ ,则称 $ x $ 比 $ y $ 更远离 $ m $ .
(1) 若 $ x-2 $ 比 $ 2x $ 更远离1,求实数 $ x $ 的取值范围;
(2) 判断 $ x < y < m $ 是 $ x $ 比 $ y $ 更远离 $ m $ 的什么条件(充分不必要条件、必要不充分条件、充要条件、既不充分也不必要条件),并加以证明;
(3) 已知 $ a > 0 $ , $ b > 0 $ ,若 $ p=\dfrac{ab+2b}{{a}^{2}+{b}^{2}+1} $ ,证明: $ p $ 比 $ \sqrt{2} $ 更远离 $ \sqrt{3} $ .
答案:(1) 【解】由题意可得 $ (x-2-1)^{2} > (2x-1)^{2} $ ,即 $ (3x-4)(x+2) < 0 $ ,解得 $ -2 < x < \dfrac{4}{3} $ ,所以实数 $ x $ 的取值范围为 $ {x|-2 < x < \dfrac{4}{3}} $ .
(2) 【解】 $ x < y < m $ 是 $ x $ 比 $ y $ 更远离 $ m $ 的充分不必要条件,证明:
①已知 $ x < y < m $ ,则 $ m-x > m-y > 0 $ ,可得
$ (m-x)^{2} > (m-y)^{2} $ ,即 $ (x-m)^{2} > (y-m)^{2} $ ,
所以 $ x < y < m $ 是 $ x $ 比 $ y $ 更远离 $ m $ 的充分条件.
②已知 $ x $ 比 $ y $ 更远离 $ m $ ,则 $ (x-m)^{2} > (y-m)^{2} $ ,举例 $ x=3 $ , $ y=2 $ , $ m=0 $ ,满足 $ (x-m)^{2} > (y-m)^{2} $ ,但不满足 $ x < y < m $ ,所以 $ x < y < m $ 不是 $ x $ 比 $ y $ 更远离 $ m $ 的必要条件.
综上, $ x < y < m $ 是 $ x $ 比 $ y $ 更远离 $ m $ 的充分不必要条件.
(3) 【证明】因为 $ a > 0 $ , $ b > 0 $ ,
$ p=\dfrac{ab+2b}{{a}^{2}+{b}^{2}+1}=\dfrac{ab+2b}{{a}^{2}+\dfrac{1}{5}{b}^{2}+\dfrac{4}{5}{b}^{2}+1}\leqslant \dfrac{ab+2b}{2\sqrt{\dfrac{1}{5}}ab+2\sqrt{\dfrac{4}{5}}b}=\dfrac{\sqrt{5}}{2} $ ,
当且仅当 $ \begin{cases}{a}^{2}=\dfrac{1}{5}{b}^{2},\\ \dfrac{4}{5}{b}^{2}=1,\end{cases} $ 即 $ \begin{cases}a=\dfrac{1}{2},\\ b=\dfrac{\sqrt{5}}{2}\end{cases} $ 时,等号成立.
因为 $ p\leqslant \dfrac{\sqrt{5}}{2} < \sqrt{2} < \sqrt{3} $ ,所以由(2)可知 $ p $ 比 $ \sqrt{2} $ 更远离 $ \sqrt{3} $ ,即得证.
解析:
