第二章高考强化

如图，设“某人”头顶至肚脐的长度为 $ a\text{ }\mathrm{c}\mathrm{m} $ ,肚脐至足底的长度为 $ b\text{ }\mathrm{c}\mathrm{m} $ ，头顶至咽喉的长度为 $ c\text{ }\mathrm{c}\mathrm{m} $ ，咽喉至肚脐的长度为 $ d\text{ }\mathrm{c}\mathrm{m} $ ,则

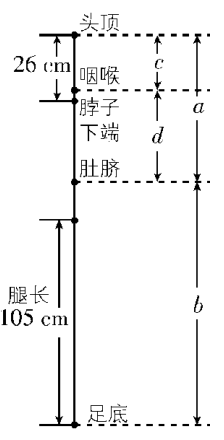
$ \dfrac{a}{b}=\dfrac{c}{d}=\dfrac{\sqrt{5}-1}{2}\approx 0.618 $ ,

$ c < 26 $ , $ b > 105 $ , $ c+d=a $ .

设“某人”的身高为 $ h\text{ }\mathrm{c}\mathrm{m} $ ，即 $ a+b=h $ .

由 $ \begin{cases}b > 105,\\ a\approx 0.618b,\end{cases} $ 解得 $ a > 64.89 $ ,

由 $ \begin{cases}c < 26,\\ c\approx 0.618d,\end{cases} $ 解得 $ d < 42.07 $ ，

所以 $ c+d < 26+42.07=68.07 $ ,即 $ a < 68.07 $ .

$ \begin{cases}a < 68.07,\\ a\approx 0.618b,\end{cases} $ 解得 $ b < 110.15 $ .

整理可得 $ 64.89+105 < a+b < 68.07+110.15 $ ，即 $ 169.89 < h < 178.22 $ ，结合选项可知其身高可能是 $ 175\text{ }\mathrm{c}\mathrm{m} $ .故选 $ \mathrm{B} $ .

由题意可知 $ \dfrac{1}{a}+\dfrac{a}{{b}^{2}}+b\geqslant 2\sqrt{\dfrac{1}{a}\cdot \dfrac{a}{{b}^{2}}}+b\geqslant 2\sqrt{\dfrac{2}{b}\cdot b}=2\sqrt{2} $ ,当且仅当 $ \dfrac{1}{a}=\dfrac{a}{{b}^{2}} $ 时,第一个“ $ = $ ”成立,当且仅当 $ \dfrac{2}{b}=b $ 时,第二个“ $ = $ ”成立,即 $ a=b=\sqrt{2} $ 时,等号同时成立, $ \dfrac{1}{a}+\dfrac{a}{{b}^{2}}+b $ 取得最小值,为 $ 2\sqrt{2} $ .

由 $ 5{x}^{2}{y}^{2}+{y}^{4}=1 $ ，可得 $ {x}^{2}=\dfrac{1-{y}^{4}}{5{y}^{2}} $ ，由 $ {x}^{2}\geqslant 0 $ ，可得 $ 0 < {y}^{2}\leqslant 1 $ ，

则 $ {x}^{2}+{y}^{2}=\dfrac{1-{y}^{4}}{5{y}^{2}}+{y}^{2}=\dfrac{1+4{y}^{4}}{5{y}^{2}}=\dfrac{1}{5}(4{y}^{2}+\dfrac{1}{{y}^{2}})\geqslant \dfrac{1}{5}\cdot 2\sqrt{4{y}^{2}\cdot \dfrac{1}{{y}^{2}}}=\dfrac{4}{5} $ ，当且仅当 $ {y}^{2}=\dfrac{1}{2} $ ， $ {x}^{2}=\dfrac{3}{10} $ 时，等号成立，

故 $ {x}^{2}+{y}^{2} $ 的最小值为 $ \dfrac{4}{5} $ .

由 $ {x}^{2}-x-6\geqslant 0 $ ，得 $ x\leqslant -2 $ 或 $ x\geqslant 3 $ ，则 $ N=｛x|x\leqslant -2 $ 或 $ x\geqslant 3｝.\because M=｛-2 $ , $ -1 {\rm ,0,1} $ , $ 2｝ $ ， $ \therefore M\cap N=｛-2｝ $ ，故选 $ \mathrm{C} $ .

由不等式 $ {x}^{2}-3x-4 < 0 $ ,解得 $ -1 < x < 4 $ ，则 $ A=｛x|-1 < x < 4｝ $ .又 $ B=｛-4,1,3,5｝ $ ,所以 $ A\cap B=｛1,3｝ $ ，故选 $ \mathrm{D} $ .

由题意, $ m=4-2a+b $ ,令 $ y=(x-c)(x-t) $ ,则由根与系数的关系知, $ c+t=-a $ , $ ct=b $ ,故 $ m=4+2(c+t)+ct $ ,又 $ 4\leqslant m\leqslant 5 $ ,则 $ -2t\leqslant c(2+t)\leqslant 1-2t $ .

因为 $ -1\leqslant t\leqslant 1 $ ,所以 $ -\dfrac{2t}{2+t}\leqslant c\leqslant \dfrac{1-2t}{2+t} $ ,

当 $ -1\leqslant t < 0 $ 时, $ \dfrac{(1-2t)t}{2+t}\leqslant ct\leqslant -\dfrac{2{t}^{2}}{2+t} $ ,即存

在 $ -1\leqslant t < 0 $ 使 $ \dfrac{(1-2t)t}{2+t}\leqslant b\leqslant -\dfrac{2{t}^{2}}{2+t} $ ,

记 $ u=t+2 $ , $ 1\leqslant u < 2 $ ,则 $ \dfrac{(1-2t)t}{2+t}=-(2u+\dfrac{10}{u}-9) $ , $ -\dfrac{2{t}^{2}}{2+t}=-2(u+\dfrac{4}{u}-4) $ ,又 $ y=2u+\dfrac{10}{u} $ 与 $ y=u+\dfrac{4}{u} $ 在 $ ｛u|1\leqslant u < 2｝ $ 上均随 $ u $ 的增大而减小，故 $ 0 > \dfrac{(1-2t)t}{2+t}\geqslant -3 $ ,

$ -2\leqslant -\dfrac{2{t}^{2}}{2+t} < 0 $ ,故 $ -3\leqslant b < 0 $ .

当 $ 0\leqslant t\leqslant 1 $ 时, $ -\dfrac{2{t}^{2}}{2+t}\leqslant b\leqslant \dfrac{(1-2t)t}{2+t} $ ,同理可

得 $ 0\geqslant -\dfrac{2{t}^{2}}{2+t}\geqslant -\dfrac{2}{3} $ , $ -\dfrac{1}{3}\leqslant \dfrac{(1-2t)t}{2+t}\leqslant 9-4\sqrt{5} $ ,故 $ -\dfrac{2}{3}\leqslant b\leqslant 9-4\sqrt{5} $ .

综上所述, $ -3\leqslant b\leqslant 9-4\sqrt{5} $ .故选 $ \mathrm{D} $ .

分离参变量得 $ m\geqslant (2x-1)(y-2x) $ 恒成立,则 $ m\geqslant [(2x-1)(y-2x)]_{ \max } $ ,故右式取最大值时 $ 2x-1 $ , $ y-2x $ 必须同号（且都不为零），此时 $ x < \dfrac{1}{2} $ ,因为若 $ x > \dfrac{1}{2} $ ,则 $ 2x-1 > 0 $ , $ y-2x $ 与其同号,则 $ y > 1 $ ,与已知矛盾.由 $ 0\leqslant x\leqslant y\leqslant 1 $ ,设 $ y=tx(1\leqslant t) $ ,则 $ (2x-1)(y-2x)=\dfrac{2-t}{2}\cdot 2x(1-2x) $ ,若要求 $ (2x-1)(y-2x) $ 取最大值，则需 $ \dfrac{2-t}{2} > 0 $ ,即 $ 1\leqslant t < 2 $ ,此时 $ (2x-1)(y-2x)=\dfrac{2-t}{2}\cdot 2x(1-2x)\leqslant \dfrac{2-t}{2}\cdot {\left(\dfrac{2x+1-2x}{2}\right) ^ {2}}=\dfrac{2-t}{8}\leqslant \dfrac{1}{8} $ ,当且仅当 $ \begin{cases}2-t > 0,\\ 1-2x=2x,\\ t=1,\end{cases} $ 即 $ x=y=\dfrac{1}{4} $ 时等号成立,所以 $ m\geqslant \dfrac{1}{8} $ .故选 $ \mathrm{B} $ .