7.已知函数 $ f(x)=|x+a|+|x-a| $ , $ g(x)=-{x}^{2}+2ax+4a $ ,其中 $ a\geqslant 1 $ .
(2) 用 $ M(x) $ 表示 $ f(x) $ , $ g(x) $ 中的较大者,记为 $ M(x)= \max {f(x) $ , $ g(x)} $ ,则当 $ x > 0 $ 时,求函数 $ M(x) $ 的解析式;
(3) 用 $ m(x) $ 表示 $ f(x) $ , $ g(x) $ 中的较小者,记为 $ m(x)= \min {f(x) $ , $ g(x)} $ ,若 $ \min {f(x) $ , $ g(x)}\leqslant 8 $ 恒成立,求实数 $ a $ 的取值范围.
答案:(1) 【解】当 $ a=1 $ 时, $ f(x)=|x+1|+|x-1| $ ,
$ x\in [-2,2] $ ,
当 $ -2\leqslant x\leqslant -1 $ 时, $ f(x)=-(x+1)-(x-1)=-2x $ ;
当 $ 1\leqslant x\leqslant 2 $ 时, $ f(x)=(x+1)+(x-1)=2x $ ;
当 $ -1 < x < 1 $ 时, $ f(x)=(x+1)-(x-1)=2 $ ,
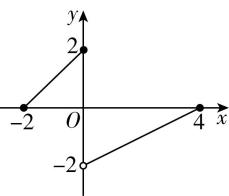
$ \therefore f(x)=\begin{cases}-2x,-2\leqslant x\leqslant -1,\\ 2,-1 < x < 1,\\ 2x,1\leqslant x\leqslant 2,\end{cases} $
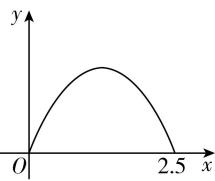
$ f(x) $ 的图象如图所示.

(2) 【解】 $ \because a\geqslant 1 $ ,
$ \therefore $ 当 $ x\leqslant -a $ 时, $ f(x)=-(x+a)-(x-a)=-2x $ ,
当 $ x\geqslant a $ 时, $ f(x)=(x+a)+(x-a)=2x $ ,
当 $ -a < x < a $ 时, $ f(x)=(x+a)-(x-a)=2a $ ,
$ \therefore f(x)=\begin{cases}-2x,x\leqslant -a,\\ 2a,-a < x < a,\\ 2x,x\geqslant a,\end{cases} $
$ \therefore $ 当 $ x > 0 $ 时, $ f(x)=\begin{cases}2a,0 < x < a,\\ 2x,x\geqslant a.\end{cases} $
$ g(x)=-{x}^{2}+2ax+4a $ 的图象开口向下,对称轴为直线 $ x=a $ ,
$ \therefore g (x)_{ \max }=g (a )=-{a}^{2}+2{a}^{2}+4a={a}^{2}+4a $ , $ g(0)=4a > 2a $ .
当 $ x > 0 $ 时,令 $ g(x)\geqslant f(x) $ ,结合图象知 $ -{x}^{2}+2ax+4a\geqslant 2x $ ,即 $ {x}^{2}+(2-2a)x-4a\leqslant 0 $ ,
即 $ (x+2)(x-2a)\leqslant 0 $ ,解得 $ 0 < x\leqslant 2a $ .
令 $ g(x) < f(x) $ ,结合图象知 $ -{x}^{2}+2ax+4a < 2x $ ,解得 $ x > 2a $ ,
$ \therefore M(x)=\begin{cases}-{x}^{2}+2ax+4a,0 < x\leqslant 2a,\\ 2x,x > 2a.\end{cases} $
(3) 【解】由(2)知 $ f(x)=\begin{cases}-2x,x\leqslant -a,\\ 2a,-a < x < a,\\ 2x,x\geqslant a.\end{cases} $
当 $ x=-a $ 时, $ f(-a)=2a $ , $ g(-a)=-{\left(-a\right) ^ {2}}+2a(-a)+4a=-3{a}^{2}+4a $ ,
令 $ ℎ(a)=2a-(-3{a}^{2}+4a)=3{a}^{2}-2a $ , $ a\geqslant 1 $ ,
则 $ ℎ(a) $ 的图象开口向上,对称轴方程为 $ a=\dfrac{1}{3} $ ,
$ \therefore $ 在 $ [1,+\mathrm{\infty }) $ 上 $ ℎ(a) $ 随着 $ a $ 的增大而增大,故 $ ℎ (a)_{ \min }=ℎ (1 )=3-2 > 0 $ ,
$ \therefore $ 记 $ g(x) $ 的图象在 $ y $ 轴左侧与线段 $ AB $ 交于点 $ C $ ,在 $ y $ 轴右侧与射线 $ y=2x(x\geqslant a) $ 交于点 $ D $ ,
$ f(x) $ , $ g(x) $ 在同一平面直角坐标系上的图象如图所示,

记点 $ C $ 的横坐标为 $ {x}_{C} $ ,由(2)知点 $ D $ 的横坐标为 $ 2a $ ,
$ \therefore m(x) $ 的图象如图所示,

由图可知,当 $ x=2a $ 时, $ m(x)_{ \max }=4a $ ,
$ \therefore 4a\leqslant 8 $ ,解得 $ a\leqslant 2 $ ,又 $ a\geqslant 1 $ , $ \therefore 1\leqslant a\leqslant 2 $ ,即实数 $ a $ 的取值范围为 $ [1,2] $ .