3.3 幂函数
一、刷基础
1.下列函数中,不是幂函数的是( )
A. $ y={\mathrm{\pi }}^{x} $
B. $ y={x}^{3} $
C. $ y=\sqrt{x} $
D. $ y=\dfrac{1}{x} $
答案:A
解析:幂函数的解析式为 $ y={x}^{\alpha }(\alpha $ 为常数 $ ) $ ,则 $ y={x}^{3} $ , $ y=\sqrt{x} $ , $ y=\dfrac{1}{x} $ 均符合幂函数的定义,
而 $ y={\mathrm{\pi }}^{x} $ 不符合幂函数的定义.故选 $ \mathrm{A} $ .
2.已知 $ f(x)=(m-4){x}^{m-\frac{9}{2}} $ 是幂函数,若 $ f(a)=2 $ ,则 $ a= $ ( )
A. $ \dfrac{1}{2} $
B.2
C.4
D.6
答案:C
解析:因为 $ f(x)=(m-4){x}^{m-\frac{9}{2}} $ 是幂函数,所以 $ m-4=1 $ ,解得 $ m=5 $ ,即 $ f(x)={x}^{\frac{1}{2}}=\sqrt{x} $ ,
若 $ f(a)=\sqrt{a}=2 $ ,则 $ a=4 $ .故选 $ \mathrm{C} $ .
3.已知函数 $ f(x)=({n}^{2}-2n-2){x}^{n} $ ,则“ $ n=-1 $ ”是“ $ f(x) $ 是幂函数”的( )
A.充分不必要条件
B.必要不充分条件
C.充要条件
D.既不充分也不必要条件
答案:A
解析:若函数 $ f(x)=({n}^{2}-2n-2){x}^{n} $ 为幂函数,则 $ {n}^{2}-2n-2=1 $ ,解得 $ n=3 $ 或 $ n=-1 $ .故“ $ n=-1 $ ”是“ $ f(x) $ 是幂函数”的充分不必要条件.故选 $ \mathrm{A} $ .
4.若幂函数 $ f(x) $ 的图象过点 $ (4,2) $ ,则 $ y=\dfrac{f(3-|x|)}{f(x)} $ 的定义域是 .
解析:设幂函数 $ f (x )={x}^{\alpha } (\alpha $ 为常数 $ ) $ ,由幂函数 $ f(x) $ 的图象过点 $ (4,2) $ 得 $ {4}^{\alpha }=2 $ ,则 $ \alpha =\dfrac{1}{2}⇒f(x)={x}^{\frac{1}{2}}=\sqrt{x} $ .
所以 $ y=\dfrac{f(3-|x|)}{f(x)}=\dfrac{\sqrt{3-|x|}}{\sqrt{x}} $ .
由 $ \begin{cases}3-\mid x\mid \geqslant 0,\\ x > 0\end{cases}⇒0 < x\leqslant 3 $ ,所以所求函数的定义域是 $ (0,3] $ .
5.直线 $ y=1 $ , $ y=x $ , $ x=1 $ 及幂函数 $ y={x}^{-1} $ 的图象将直角坐标系第一象限分为8个部分(如图所示),那么幂函数 $ y={x}^{-\frac{1}{3}} $ 的图象在第一象限中经过( )
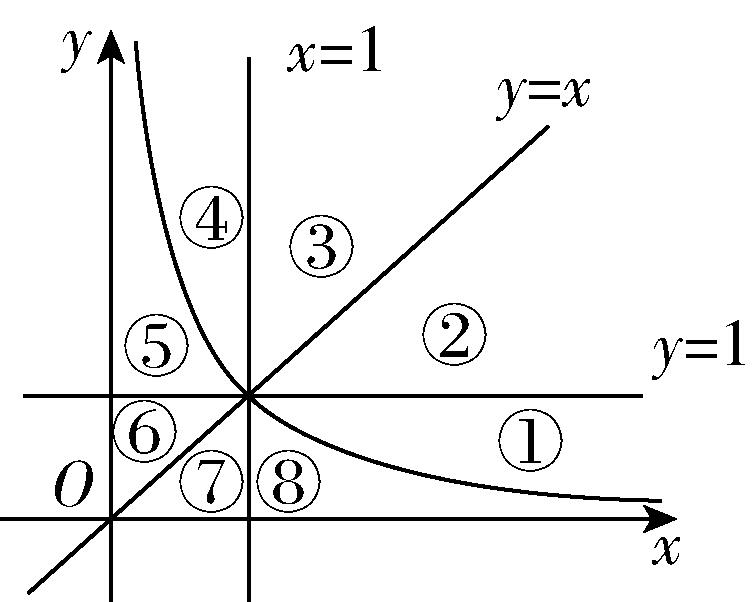
A.③⑦
B.③⑧
C.④⑦
D.①⑤
答案:D
解析:在第一象限内,直线 $ x=1 $ 的左侧,幂函数的指数越大图象越接近于 $ x $ 轴, $ \because -\dfrac{1}{3} > -1 $ , $ \therefore $ 直线在 $ x=1 $ 的左侧 $ y={x}^{-\frac{1}{3}} $ 的图象位于 $ y={x}^{-1} $ 图象的左侧,故经过⑤;
在第一象限内,直线 $ x=1 $ 的右侧,幂函数的指数越小图象越接近于 $ x $ 轴, $ \therefore $ 直线在 $ x=1 $ 的右侧 $ y={x}^{-\frac{1}{3}} $ 的图象位于 $ y={x}^{-1} $ 图象的上方, $ y=1 $ 的下方,故经过①.故选 $ \mathrm{D} $ .
6.如图的曲线是幂函数 $ y={x}^{n} $ 在第一象限内的图象.已知 $ n $ 分别取 $ ±2 $ , $ ±\dfrac{1}{2} $ 四个值,与曲线 $ {C}_{1} $ , $ {C}_{2} $ , $ {C}_{3} $ , $ {C}_{4} $ 相应的 $ n $ 依次为( )
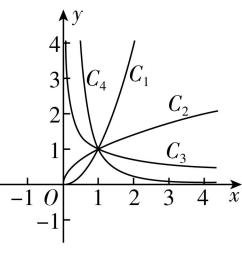
A. $ {\rm 2,} \dfrac{1}{2} $ , $ -\dfrac{1}{2} $ , $ -2 $
B. $ {\rm 2,} \dfrac{1}{2} $ , $ -2 $ , $ -\dfrac{1}{2} $
C. $ -\dfrac{1}{2} $ , $ -2 {\rm ,2} $ , $ \dfrac{1}{2} $
D. $ -2 $ , $ -\dfrac{1}{2} $ , $ \dfrac{1}{2} {\rm ,2} $
答案:A
解析:曲线 $ {C}_{1} $ , $ {C}_{2} $ 单调递增且 $ {C}_{2} $ 趋于平缓,所以曲线 $ {C}_{1} $ , $ {C}_{2} $ 相应的 $ n $ 的值分别为 $ {\rm 2,} \dfrac{1}{2} $ ;曲线 $ {C}_{3} $ , $ {C}_{4} $ 单调递减且曲线 $ {C}_{3} $ 在直线 $ x=1 $ 右侧更高,故曲线 $ {C}_{3} $ , $ {C}_{4} $ 相应的 $ n $ 的值分别为 $ -\dfrac{1}{2} $ , $ -2 $ .故选 $ \mathrm{A} $ .
7.在同一平面直角坐标系内,函数 $ y={x}^{a}(a\ne 0) $ 和 $ y=ax-\dfrac{1}{a} $ 的图象可能是( )
A.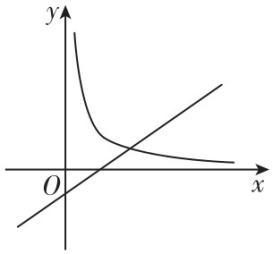
B.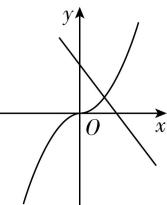
C.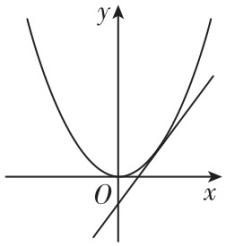
D.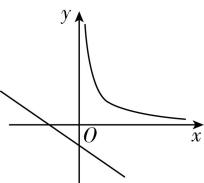
答案:C
解析:对于 $ \mathrm{A} $ ,由函数 $ y={x}^{a}(a\ne 0) $ 的图象可知 $ a < 0 $ ,由 $ y=ax-\dfrac{1}{a} $ 的图象可知 $ a > 0 $ ,互相矛盾, $ \mathrm{A} $ 不符合题意;
对于 $ \mathrm{B} $ ,由函数 $ y={x}^{a}(a\ne 0) $ 的图象可知 $ a > 1 $ ,由 $ y=ax-\dfrac{1}{a} $ 的图象可知 $ a < 0 $ ,互相矛盾, $ \mathrm{B} $ 不符合题意;
对于 $ \mathrm{C} $ ,由函数 $ y={x}^{a}(a\ne 0) $ 的图象可知 $ a > 1 $ ,由 $ y=ax-\dfrac{1}{a} $ 的图象可知 $ a > 1 $ 且 $ -\dfrac{1}{a} < 0 $ , $ \mathrm{C} $ 符合题意;
对于 $ \mathrm{D} $ ,由函数 $ y={x}^{a}(a\ne 0) $ 的图象可知 $ a < 0 $ ,由 $ y=ax-\dfrac{1}{a} $ 的图象可知 $ a < 0 $ 且 $ -\dfrac{1}{a} < 0 $ ,互相矛盾, $ \mathrm{D} $ 不符合题意.故选 $ \mathrm{C} $ .
8.若幂函数 $ f(x) $ 的图象过点 $ (4,2) $ ,则不等式 $ f(x) < f({x}^{2}) $ 的解集为( )
A. $ (-\mathrm{\infty },0)\cup (1,+\mathrm{\infty }) $
B. $ (0,1) $
C. $ (-\mathrm{\infty },0) $
D. $ (1,+\mathrm{\infty }) $
答案:D
解析:设幂函数 $ f (x )={x}^{\alpha } (\alpha $ 为常数 $ ) $ ,由幂函数 $ f(x) $ 的图象过点 $ (4,2) $ 得 $ {4}^{\alpha }=2 $ ,解得 $ \alpha =\dfrac{1}{2} $ ,则 $ f(x)={x}^{\frac{1}{2}} $ .
因为函数 $ f(x)={x}^{\frac{1}{2}} $ 在定义域 $ [0,+\mathrm{\infty }) $ 上单调递增,所以不等式 $ f(x) < f({x}^{2})⇔0\leqslant x < {x}^{2} $ ,解得 $ x > 1 $ ,
所以原不等式的解集为 $ (1,+\mathrm{\infty }) $ .故选 $ \mathrm{D} $ .
9.(多选)下列说法正确的是( )(多选)
A.所有幂函数的图象均过点 $ (0,0) $
B.若幂函数的图象经过点 $ (\dfrac{1}{8},2) $ ,则解析式为 $ y={x}^{-\frac{1}{3}} $
C.幂函数一定具有奇偶性
D.任何幂函数的图象都不经过第四象限
答案:BD
解析:对于 $ \mathrm{A} $ 项:例如 $ y=\dfrac{1}{x} $ ,图象不过点 $ (0,0) $ ,故 $ \mathrm{A} $ 错误;
对于 $ \mathrm{B} $ 项:设幂函数为 $ y={x}^{\alpha } $ ,幂函数的图象经过点 $ (\dfrac{1}{8},2) $ ,则 $ 2={(\dfrac{1}{8})}^{\alpha } $ ,解得 $ \alpha =-\dfrac{1}{3} $ ,所以 $ y={x}^{-\frac{1}{3}} $ ,故 $ \mathrm{B} $ 正确;
对于 $ \mathrm{C} $ 项:例如 $ y=\sqrt{x} $ ,其定义域不关于原点对称,不具有奇偶性,故 $ \mathrm{C} $ 错误;
对于 $ \mathrm{D} $ 项:任何幂函数的图象都不经过第四象限,故 $ \mathrm{D} $ 正确.故选 $ \mathrm{B}\mathrm{D} $ .
10.(多选)已知幂函数 $ f(x) $ 的图象经过点 $ (9,3) $ ,则( )(多选)
A.函数 $ f(x) $ 为减函数
B.函数 $ f(x) $ 为偶函数
C.当 $ x\geqslant 4 $ 时, $ f(x)\geqslant 2 $
D.当 $ {x}_{2} > {x}_{1} > 0 $ 时, $ \dfrac{f({x}_{1})+f({x}_{2})}{2} < f(\dfrac{{x}_{1}+{x}_{2}}{2}) $
答案:CD
解析:设幂函数 $ f(x)={x}^{\alpha } $ ,则 $ f(9)={9}^{\alpha }=3 $ ,解得 $ \alpha =\dfrac{1}{2} $ ,所以 $ f(x)={x}^{\frac{1}{2}} $ ,定义域为 $ [0,+\mathrm{\infty }) $ .
$ \mathrm{A} $ 选项,因为 $ \dfrac{1}{2} > 0 $ ,所以 $ f(x) $ 在 $ [0,+\mathrm{\infty }) $ 上为增函数,故 $ \mathrm{A} $ 错误;
$ \mathrm{B} $ 选项,因为 $ f(x) $ 的定义域不关于原点对称,所以函数 $ f(x) $ 不是偶函数,故 $ \mathrm{B} $ 错误;
$ \mathrm{C} $ 选项,由 $ \mathrm{A} $ 可知, $ f(x) $ 在 $ [0,+\mathrm{\infty }) $ 上单调递增,故当 $ x\geqslant 4 $ 时, $ f(x)\geqslant f(4)={4}^{\frac{1}{2}}=2 $ ,故 $ \mathrm{C} $ 正确;
$ \mathrm{D} $ 选项,当 $ {x}_{2} > {x}_{1} > 0 $ 时,
$ {[\dfrac{f({x}_{1})+f({x}_{2})}{2}]}^{2}-{[f(\dfrac{{x}_{1}+{x}_{2}}{2})]}^{2} $
$ =\dfrac{{x}_{1}+{x}_{2}+2\sqrt{{x}_{1}{x}_{2}}}{4}-\dfrac{{x}_{1}+{x}_{2}}{2} $
$ =\dfrac{2\sqrt{{x}_{1}{x}_{2}}-{x}_{1}-{x}_{2}}{4}=-\dfrac{{\left(\sqrt{{x}_{1}}-\sqrt{{x}_{2}}\right) ^ {2}}}{4} < 0 $ ,
又 $ f(x)\geqslant 0 $ ,所以 $ \dfrac{f({x}_{1})+f({x}_{2})}{2} < f(\dfrac{{x}_{1}+{x}_{2}}{2}) $ , $ \mathrm{D} $ 正确.故选 $ \mathrm{C}\mathrm{D} $ .
11.已知 $ a={(\dfrac{2}{5})}^{0.3} $ , $ b={(\dfrac{1}{4})}^{0.3} $ , $ c={(\dfrac{1}{4})}^{-0.3} $ ,则 $ a $ , $ b $ , $ c $ 的大小关系为( )
A. $ a < c < b $
B. $ a < b < c $
C. $ b < c < a $
D. $ b < a < c $
答案:D
解析: $ c={(\dfrac{1}{4})}^{-0.3}={4}^{0.3} $ ,幂函数 $ f(x)={x}^{0.3} $ 在 $ (0,+\mathrm{\infty }) $ 上单调递增,因为 $ \dfrac{1}{4} < \dfrac{2}{5} < 4 $ ,所以 $ f(\dfrac{1}{4}) < f(\dfrac{2}{5}) < f(4) $ ,即 $ {(\dfrac{1}{4})}^{0.3} < {(\dfrac{2}{5})}^{0.3} < {4}^{0.3} $ ,所以 $ b < a < c $ ,故选 $ \mathrm{D} $ .
12.若幂函数 $ f(x)=({m}^{2}-m-1){x}^{2m-1} $ 在 $ (0,+\mathrm{\infty }) $ 上单调递增,则实数 $ m= $ .
解析:由幂函数 $ f(x)=({m}^{2}-m-1)\cdot {x}^{2m-1} $ 在 $ (0,+\mathrm{\infty }) $ 上单调递增,
得 $ \begin{cases}{m}^{2}-m-1=1,\\ 2m-1 > 0,\end{cases} $ 解得 $ m=2 $ ,所以实数 $ m=2 $ .
13.已知幂函数 $ f(x)=({m}^{2}+4m+4){x}^{m+2} $ 在 $ (0,+\mathrm{\infty }) $ 上单调递减,若 $ (2a-1)^{-m} < (a+3)^{-m} $ ,则 $ a $ 的取值范围为 .
答案: $ (-\mathrm{\infty },4) $
解析:若幂函数 $ f(x)=({m}^{2}+4m+4){x}^{m+2} $ 在 $ (0,+\mathrm{\infty }) $ 上单调递减,则 $ \begin{cases}{m}^{2}+4m+4=1,\\ m+2 < 0,\end{cases} $ 解得 $ m=-3 $ .
不等式 $ (2a-1)^{-m} < (a+3)^{-m} $ 化为 $ (2a-1)^{3} < (a+3)^{3} $ ,显然幂函数 $ y={x}^{3} $ 在 $ \boldsymbol{R} $ 上单调递增,
因此 $ 2a-1 < a+3 $ ,解得 $ a < 4 $ ,
所以 $ a $ 的取值范围为 $ (-\mathrm{\infty },4) $ .
14.幂函数 $ f(x)=({k}^{2}-5k+7){x}^{k-1} $ 为偶函数, $ g(x)=mf(x)-x-1 $ .
(1) 求函数 $ f(x) $ 的解析式;
(2) 若 $ g(x)\geqslant m(x-1) $ 对于 $ x\in [0,2] $ 恒成立,求 $ m $ 的取值范围.
答案:(1) 【解】因为函数 $ f(x)=({k}^{2}-5k+7){x}^{k-1} $ 为幂函数,
所以 $ {k}^{2}-5k+7=1 $ ,解得 $ k=2 $ 或 $ k=3 $ .
当 $ k=3 $ 时, $ f(x)={x}^{2} $ ,定义域为 $ \boldsymbol{R} $
,且 $ f(-x)={\left(-x\right) ^ {2}}={x}^{2}=f(x) $ ,
所以 $ f(x) $ 为偶函数,符合题意;
当 $ k=2 $ 时, $ f(x)=x $ ,定义域为 $ \boldsymbol{R} $ ,且 $ f(-x)=-x=-f(x) $ ,
所以 $ f(x) $ 为奇函数,不符合题意.
所以 $ f(x)={x}^{2} $ .
(2) 【解】因为 $ g(x)=mf(x)-x-1=m{x}^{2}-x-1 $ ,
所以 $ g(x)\geqslant m(x-1) $ 对于 $ x\in [0,2] $ 恒成立,即 $ m({x}^{2}-x+1)\geqslant x+1 $ 对于 $ x\in [0,2] $ 恒成立,又 $ {x}^{2}-x+1={\left(x-\dfrac{1}{2}\right) ^ {2}}+\dfrac{3}{4}\geqslant \dfrac{3}{4} $ ,
则 $ m\geqslant \dfrac{x+1}{{x}^{2}-x+1} $ 对于 $ x\in [0,2] $ 恒成立,所以 $ m\geqslant {(\dfrac{x+1}{{x}^{2}-x+1})}_{ \max } $ .
设 $ x+1=t $ ,则 $ t\in [1,3] $ , $ \dfrac{x+1}{{x}^{2}-x+1}=\dfrac{t}{{\left(t-1\right) ^ {2}}-(t-1)+1}=\dfrac{t}{{t}^{2}-3t+3}=\dfrac{1}{t-3+\dfrac{3}{t}} $ ,
因为 $ t+\dfrac{3}{t}\geqslant 2\sqrt{t\cdot \dfrac{3}{t}}=2\sqrt{3} $ ,当且仅当 $ t=\dfrac{3}{t} $ ,即 $ t=\sqrt{3} $ ,即 $ x=\sqrt{3}-1 $ 时等号成立,
所以 $ t+\dfrac{3}{t}-3\geqslant 2\sqrt{3}-3 $ , $ \dfrac{1}{t+\dfrac{3}{t}-3}\leqslant \dfrac{1}{2\sqrt{3}-3}=\dfrac{2\sqrt{3}+3}{3} $ ,
所以 $ {(\dfrac{x+1}{{x}^{2}-x+1})}_{ \max }=\dfrac{2\sqrt{3}+3}{3} $ ,
故 $ m $ 的取值范围为 $ [\dfrac{2\sqrt{3}+3}{3},+\mathrm{\infty }) $ .
解析:
15.有四个幂函数: $ \mathrm{①}f(x)={x}^{-1} $ ; $ \mathrm{②}f(x)={x}^{-2} $ ; $ \mathrm{③}f(x)={x}^{3} $ ; $ \mathrm{④}f(x)={x}^{\frac{1}{3}} $ .某同学研究了其中的一个函数,他给出这个函数的三个性质:(1)偶函数;(2)值域是 $ {y|y\in \mathrm{R} $ ,且 $ y\ne 0} $ ;(3)在 $ (-\mathrm{\infty },0) $ 上单调递增.如果他给出的三个性质中,有两个正确,一个错误,那么他研究的函数是( )
A.①
B.②
C.③
D.④
答案:B
解析: $ \mathrm{①}f(x)={x}^{-1} $ 只满足值域是 $ {y|y\in \boldsymbol{R} $ ,且 $ y\ne 0} $ ;
$ \mathrm{③}f(x)={x}^{3} $ 只满足在 $ (-\mathrm{\infty },0) $ 上单调递增;
$ \mathrm{④}f(x)={x}^{\frac{1}{3}} $ 只满足在 $ (-\mathrm{\infty },0) $ 上单调递增;
$ \mathrm{②}f(x)={x}^{-2} $ 是偶函数,在 $ (-\mathrm{\infty },0) $ 上单调递增,但其值域是 $ {y|y > 0} $ .故选 $ \mathrm{B} $ .
16.(多选)已知 $ a\in {-2,\dfrac{1}{2},1,4} $ ,若 $ F(x)={x}^{a} $ 为偶函数,则满足要求的 $ a $ 有( )(多选)
A. $ -2 $
B.1
C.4
D. $ \dfrac{1}{2} $
答案:AC
解析:当 $ a=-2 $ 时, $ F(x)={x}^{-2} $ ,定义域为 $ {x|x\ne 0} $ ,关于原点对称,且 $ F(-x)={\left(-x\right) ^ {-2}}={x}^{-2}=F(x) $ ,所以 $ F(x)={x}^{-2} $ 为偶函数,故 $ \mathrm{A} $ 正确;
当 $ a=1 $ 时, $ F(x)=x $ ,定义域为 $ \boldsymbol{R} $ ,且 $ F(x)=x $ 为奇函数,故 $ \mathrm{B} $ 错误;
当 $ a=4 $ 时, $ F(x)={x}^{4} $ ,定义域为 $ \boldsymbol{R} $ ,且 $ F(-x)={\left(-x\right) ^ {4}}={x}^{4}=F(x) $ ,
所以 $ F(x)={x}^{4} $ 为偶函数,故 $ \mathrm{C} $ 正确;
当 $ a=\dfrac{1}{2} $ 时, $ F(x)={x}^{\frac{1}{2}}=\sqrt{x} $ ,定义域为 $ [0,+\mathrm{\infty }) $ ,不关于原点对称,所以 $ F(x)={x}^{\frac{1}{2}} $ 为非奇非偶函数,故 $ \mathrm{D} $ 错误.
故选 $ \mathrm{A}\mathrm{C} $ .
17.已知幂函数 $ y=({m}^{2}-3){x}^{m} $ 的图象不过原点,则实数 $ m $ 的取值为( )
A. $ -2 $
B.0
C.2
D.2或 $ -2 $
答案:A
解析:因为 $ y=({m}^{2}-3){x}^{m} $ 为幂函数,所以 $ {m}^{2}-3=1 $ ,解得 $ m=±2 $ .
当 $ m=2 $ 时, $ y={x}^{2} $ ,图象过原点,不合题意,舍去;
当 $ m=-2 $ 时, $ y={x}^{-2} $ ,图象不过原点,符合题意.
综上所述, $ m=-2 $ .故选 $ \mathrm{A} $ .
18.已知幂函数 $ f(x) $ 的图象经过 $ A(2,\sqrt{2}) $ , $ B(1,1) $ , $ C(3,\dfrac{1}{9}) $ , $ D(\dfrac{1}{2},\dfrac{1}{4}) $ 四点中的两点,且 $ f(x) $ 在 $ (0,+\mathrm{\infty }) $ 上单调递减.
(1) 求 $ f(x) $ 的解析式;
(2) 若 $ f(a+1)=f(2a-3) $ ,求实数 $ a $ 的值.
答案:(1) 【解】方法一:设 $ f (x )={x}^{\alpha } (\alpha $ 为常数 $ ) $ ,
易知幂函数 $ f(x) $ 的图象必过点 $ B(1,1) $ ,
当幂函数 $ f(x) $ 的图象经过点 $ A(2,\sqrt{2}) $ 时, $ {2}^{\alpha }=\sqrt{2}={2}^{\frac{1}{2}} $ ,所以 $ \alpha =\dfrac{1}{2} $ ,
则 $ f(x)={x}^{\frac{1}{2}} $ 在 $ (0,+\mathrm{\infty }) $ 上单调递增,不符合题意;
当幂函数 $ f(x) $ 的图象经过点 $ C(3,\dfrac{1}{9}) $ 时, $ {3}^{\alpha }=\dfrac{1}{9}={3}^{-2} $ ,所以 $ \alpha =-2 $ ,
$ f(x)={x}^{-2} $ 在 $ (0,+\mathrm{\infty }) $ 上单调递减,符合题意;
当幂函数 $ f(x) $ 的图象经过点 $ D(\dfrac{1}{2},\dfrac{1}{4}) $ 时, $ {(\dfrac{1}{2})}^{\alpha }=\dfrac{1}{4}={\left(\dfrac{1}{2}\right) ^ {2}} $ ,所以 $ \alpha =2 $ ,
$ f(x)={x}^{2} $ 在 $ (0,+\mathrm{\infty }) $ 上单调递增,不符合题意,
故 $ f(x)={x}^{-2} $ .
方法二:设 $ f (x )={x}^{\alpha } (\alpha $ 为常数 $ ) $ ,
易知幂函数 $ f(x) $ 的图象必过点 $ B(1,1) $ ,
因为 $ f(x) $ 在 $ (0,+\mathrm{\infty }) $ 上单调递减,所以 $ C(3,\dfrac{1}{9}) $ 在 $ f(x) $ 的图象上,
所以 $ {3}^{\alpha }=\dfrac{1}{9}={3}^{-2} $ ,所以 $ \alpha =-2 $ ,
故 $ f(x)={x}^{-2} $ .
(2) 【解】易知 $ f(x)={x}^{-2} $ 的定义域为 $ {x|x\ne 0} $ ,且为偶函数,
由 $ f(a+1)=f(2a-3) $ 可得, $ |a+1|=|2a-3|\ne 0 $ .
方法一:两边同时平方并整理得, $ 3{a}^{2}-14a+8=0 $ ,
解得 $ a=\dfrac{2}{3} $ 或 $ a=4 $ .
故实数 $ a $ 的值为4或 $ \dfrac{2}{3} $ .
方法二: $ a+1=2a-3 $ 或 $ a+1=-(2a-3) $ ,
解得 $ a=4 $ 或 $ a=\dfrac{2}{3} $ .
故实数 $ a $ 的值为4或 $ \dfrac{2}{3} $ .
解析:
二、刷能力
1.若幂函数 $ f(x)={x}^{\alpha } $ 图象过点 $ (\dfrac{1}{2},\dfrac{1}{8}) $ ,且 $ f(a+2) < f(2a) $ ,则实数 $ a $ 的取值范围是( )
A. $ (-\mathrm{\infty },2) $
B. $ (2,+\mathrm{\infty }) $
C. $ (-2,2) $
D. $ (-2,+\mathrm{\infty }) $
答案:B
解析:由已知条件可得 $ f(\dfrac{1}{2})={(\dfrac{1}{2})}^{\alpha }=\dfrac{1}{8} $ ,解得 $ \alpha =3 $ ,则 $ f(x)={x}^{3} $ ,
所以函数 $ f(x) $ 在 $ \boldsymbol{R} $ 上为增函数.
由 $ f(a+2) < f(2a) $ 可得 $ a+2 < 2a $ ,解得 $ a > 2 $ .故选 $ \mathrm{B} $ .
2.已知幂函数 $ f(x) $ 的图象过点 $ (8,\dfrac{\sqrt{2}}{4}) $ ,则 $ f(x-2{x}^{2}) $ 的定义域为( )
A. $ (0,2) $
B. $ (0,\dfrac{1}{2}) $
C. $ (0,2] $
D. $ [0,\dfrac{1}{2}] $
答案:B
解析: $ \because f(x) $ 是幂函数, $ \therefore $ 设 $ f(x)={x}^{m} $ ,将 $ (8,\dfrac{\sqrt{2}}{4}) $ 代入解析式,
得 $ {8}^{m}=\dfrac{\sqrt{2}}{4} $ ,解得 $ m=-\dfrac{1}{2} $ ,故 $ f(x)={x}^{-\frac{1}{2}}=\dfrac{1}{\sqrt{x}} $ ,则 $ f(x-2{x}^{2})=\dfrac{1}{\sqrt{x-2{x}^{2}}} $ ,
故 $ x-2{x}^{2} > 0 $ ,解得 $ x\in (0,\dfrac{1}{2}) $ .故选 $ \mathrm{B} $ .
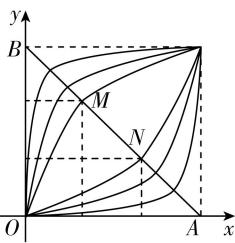
3.已知幂函数 $ y={x}^{\alpha } $ ,当 $ \alpha $ 取不同的正数时,在区间 $ [0,1] $ 上它们的图象是一簇曲线(如图).设点 $ A(1,0) $ , $ B(0,1) $ ,连接 $ AB $ ,线段 $ AB $ 恰好被其中的两个幂函数 $ y={x}^{\alpha } $ , $ y={x}^{\beta } $ 的图象三等分,即有 $ BM=MN=NA $ ,那么 $ \alpha \beta = $ ( )
A. $ \dfrac{1}{3} $
B. $ \dfrac{2}{3} $
C.1
D.3
答案:C
解析:因为点 $ A(1,0) $ , $ B(0,1) $ , $ BM=MN=NA $ ,所以 $ M(\dfrac{1}{3},\dfrac{2}{3}) $ , $ N(\dfrac{2}{3},\dfrac{1}{3}) $ ,不妨令点 $ M $ , $ \mathbf{N} $ 分别在函数 $ y={x}^{\alpha } $ , $ y={x}^{\beta } $ 的图象上,将点 $ M $ , $ \mathbf{N} $ 的坐标分别代入 $ y={x}^{\alpha } $ , $ y={x}^{\beta } $ 中,得 $ \dfrac{2}{3}={(\dfrac{1}{3})}^{\alpha } $ , $ \dfrac{1}{3}={(\dfrac{2}{3})}^{\beta } $ ,所以 $ {(\dfrac{1}{3})}^{\alpha \beta }={[{(\dfrac{1}{3})}^{\alpha }]}^{\beta }={(\dfrac{2}{3})}^{\beta }=\dfrac{1}{3} $ ,所以 $ \alpha \beta =1 $ .故选 $ \mathrm{C} $ .
4.设 $ a={(\dfrac{3}{4})}^{\frac{1}{2}} $ , $ b={(\dfrac{4}{3})}^{\frac{1}{4}} $ , $ c={(\dfrac{2}{3})}^{\frac{3}{4}} $ ,则 $ a $ , $ b $ , $ c $ 的大小关系是( )
A. $ c < a < b $
B. $ c < b < a $
C. $ a < c < b $
D. $ b < c < a $
答案:A
解析:因为 $ a={(\dfrac{3}{4})}^{\frac{1}{2}} $ , $ c={(\dfrac{2}{3})}^{\frac{3}{4}} $ ,
所以 $ a={[{\left(\dfrac{3}{4}\right) ^ {2}}]}^{\frac{1}{4}}={(\dfrac{9}{16})}^{\frac{1}{4}} $ , $ c={[{\left(\dfrac{2}{3}\right) ^ {3}}]}^{\frac{1}{4}}={(\dfrac{8}{27})}^{\frac{1}{4}} $ .
因为函数 $ y={x}^{\frac{1}{4}} $ 为增函数, $ \dfrac{8}{27} < \dfrac{9}{16} < \dfrac{4}{3} $ ,
所以 $ {(\dfrac{8}{27})}^{\frac{1}{4}} < {(\dfrac{9}{16})}^{\frac{1}{4}} < {(\dfrac{4}{3})}^{\frac{1}{4}} $ ,故 $ c < a < b $ .
故选 $ \mathrm{A} $ .
5.已知函数 $ f(x)=\sqrt[3]{x}+x+1 $ ,若 $ f(1-m)+f(2m) > 2 $ ,则 $ m $ 的取值范围是( )
A. $ (-1,+\mathrm{\infty }) $
B. $ (1,+\mathrm{\infty }) $
C. $ (-\mathrm{\infty },-1) $
D. $ (-\mathrm{\infty },1) $
答案:A
解析:令 $ g(x)=f(x)-1=\sqrt[3]{x}+x $ ,因为 $ g(x) $ 的定义域为 $ \boldsymbol{R} $ ,关于原点对称,且 $ g(-x)=\sqrt[3]{-x}+(-x)=-\sqrt[3]{x}-x=-g(x) $ ,
所以 $ g(x) $ 是 $ \boldsymbol{R} $ 上的奇函数.
因为幂函数 $ y=\sqrt[3]{x} $ , $ y=x $ 都是 $ \boldsymbol{R} $ 上的增函数,
所以 $ g(x) $ 是 $ \boldsymbol{R} $ 上的增函数.
又 $ f(1-m)+f(2m) > 2⇔f(1-m)-1 > -(f(2m)-1)⇔g(1-m) > -g(2m)=g(-2m) $ ,
所以 $ 1-m > -2m $ ,解得 $ m > -1 $ ,
所以 $ m $ 的取值范围是 $ (-1,+\mathrm{\infty }) $ .故选 $ \mathrm{A} $ .
6.(多选)已知幂函数 $ f(x) $ 的图象经过点 $ (\dfrac{1}{8},\dfrac{\sqrt{2}}{4}) $ , $ P({x}_{1},{y}_{1}) $ , $ Q({x}_{2},{y}_{2})(0 < {x}_{1} < {x}_{2}) $ 是函数图象上任意不同的两点,则下列结论正确的有( )(多选)
A. $ {x}_{1}f({x}_{1}) > {x}_{2}f({x}_{2}) $
B. $ {x}_{1}f({x}_{2}) < {x}_{2}f({x}_{1}) $
C. $ \dfrac{f({x}_{1})}{{x}_{1}} > \dfrac{f({x}_{2})}{{x}_{2}} $
D. $ \dfrac{f({x}_{1})}{{x}_{1}} < \dfrac{f({x}_{2})}{{x}_{2}} $
答案:BC
解析:设幂函数 $ f(x)={x}^{\alpha } $ ,则有 $ {(\dfrac{1}{8})}^{\alpha }={2}^{-3\alpha }=\dfrac{\sqrt{2}}{4}={2}^{-\frac{3}{2}} $ ,解得 $ \alpha =\dfrac{1}{2} $ ,所以 $ f(x)=\sqrt{x}(x\geqslant 0) $ .
作出函数 $ f(x) $ 的大致图象如图所示,由其图象知图象上的点与原点连线所在直线的倾斜程度随 $ x $ 的增大而减小,即 $ \dfrac{f({x}_{2})}{{x}_{2}} < \dfrac{f({x}_{1})}{{x}_{1}} $ ,即 $ {x}_{1}f({x}_{2}) < {x}_{2}f({x}_{1}) $ ,所以 $ \mathrm{B} $ , $ \mathrm{C} $ 正确.

7.已知函数 $ f(x)=\sqrt[3]{x} $ ,若正数 $ a $ , $ b $ 满足 $ f(a+1)+f(b-2)=0 $ ,则 $ a+b+2ab $ 的最大值是 .
解析:由题意得 $ f(x)=\sqrt[3]{x} $ 的定义域为 $ \boldsymbol{R} $ ,且 $ f(-x)=\sqrt[3]{-x}=-\sqrt[3]{x}=-f(x) $ ,
所以 $ f(x) $ 为奇函数, $ f(x)+f(-x)=0 $ ,且函数 $ f(x) $ 单调递增.
因为 $ f(a+1)+f(b-2)=0 $ ,所以 $ -(a+1)=b-2 $ ,化简得 $ a+b=1 $ .
所以 $ a+b+2ab=1+2ab\leqslant 1+2×{\left(\dfrac{a+b}{2}\right) ^ {2}}=\dfrac{3}{2} $ ,
当且仅当 $ a=b=\dfrac{1}{2} $ 时取等号,故 $ a+b+2ab $ 的最大值是 $ \dfrac{3}{2} $ .
8.已知 $ A={\alpha $ , $ \beta }\subseteq {-1,\dfrac{1}{2},2,3} $ ,若函数 $ f(x)={x}^{\alpha } $ 与 $ g(x)={x}^{\beta } $ 的图象只有1个交点,则写出一个符合条件的集合 $ A= $ ;若有两个交点,则满足条件的不同集合 $ A $ 有 个.
答案: $ {-1,\dfrac{1}{2}} $ (答案不唯一); 4
解析:函数 $ y={x}^{-1} $ 的图象与 $ y={x}^{\frac{1}{2}} $ , $ y={x}^{2} $ , $ y={x}^{3} $ 的图象分别有1个,1个,2个交点;
函数 $ y={x}^{\frac{1}{2}} $ 的图象与 $ y={x}^{2} $ , $ y={x}^{3} $ 的图象都有2个交点;
函数 $ y={x}^{2} $ 的图象与 $ y={x}^{3} $ 的图象有2个交点.
若函数 $ f(x)={x}^{\alpha } $ 与 $ g(x)={x}^{\beta } $ 的图象只有1个交点,则 $ A={-1,\dfrac{1}{2}} $ 或 $ A={-1 $ , $ 2} $ .
若函数 $ f(x)={x}^{\alpha } $ 与 $ g(x)={x}^{\beta } $ 的图象只有2个交点,
则 $ A={-1 $ , $ 3} $ 或 $ {\dfrac{1}{2},2} $ 或 $ {\dfrac{1}{2},3} $ 或 $ {2,3} $ .
9.已知幂函数 $ f(x)=(8{m}^{2}-1){x}^{m} $ 的图象过点 $ (-m,n) $ .
(1) 求实数 $ n $ 的值;
(2) 设函数 $ g(x)=f(x)+\dfrac{1}{f(x)} $ ,用定义证明: $ g(x) $ 在 $ (0,1) $ 上单调递减.
答案:(1) 【解】由函数 $ f(x)=(8{m}^{2}-1){x}^{m} $ 是幂函数,得 $ 8{m}^{2}-1=1 $ ,解得 $ m=±\dfrac{1}{2} $ .
当 $ m=\dfrac{1}{2} $ 时,函数 $ y={x}^{\frac{1}{2}} $ 的定义域为 $ [0,+\mathrm{\infty }) $ ,显然此函数图象不可能过点 $ (-\dfrac{1}{2},n) $ ,即 $ m=\dfrac{1}{2} $ 不符合题意;
当 $ m=-\dfrac{1}{2} $ 时,函数 $ y={x}^{-\frac{1}{2}} $ 的定义域为 $ (0,+\mathrm{\infty }) $ ,显然此函数图象可以过点 $ (\dfrac{1}{2},n) $ ,
所以 $ m=-\dfrac{1}{2} $ ,函数 $ f(x)={x}^{-\frac{1}{2}} $ , $ n=f(\dfrac{1}{2})={(\dfrac{1}{2})}^{-\frac{1}{2}}=\sqrt{2} $ .
(2) 【证明】由(1)知,函数 $ f(x)={x}^{-\frac{1}{2}} $ ,则函数 $ g(x)={x}^{-\frac{1}{2}}+{x}^{\frac{1}{2}}=\sqrt{x}+\dfrac{1}{\sqrt{x}} $ .
任取 $ {x}_{1} $ , $ {x}_{2}\in (0,1) $ ,且 $ {x}_{1} < {x}_{2} $ ,则 $ g({x}_{1})-g({x}_{2})=\sqrt{{x}_{1}}+\dfrac{1}{\sqrt{{x}_{1}}}-(\sqrt{{x}_{2}}+\dfrac{1}{\sqrt{{x}_{2}}})=(\sqrt{{x}_{1}}-\sqrt{{x}_{2}})(1-\dfrac{1}{\sqrt{{x}_{1}{x}_{2}}}) $ ,
由 $ 0 < {x}_{1} < {x}_{2} < 1 $ ,得 $ 0 < \sqrt{{x}_{1}} < \sqrt{{x}_{2}} < 1 $ ,且 $ 0 < \sqrt{{x}_{1}{x}_{2}} < 1 $ ,因此 $ \sqrt{{x}_{1}}-\sqrt{{x}_{2}} < 0 $ , $ 1-\dfrac{1}{\sqrt{{x}_{1}{x}_{2}}} < 0 $ ,
则 $ (\sqrt{{x}_{1}}-\sqrt{{x}_{2}})(1-\dfrac{1}{\sqrt{{x}_{1}{x}_{2}}}) > 0 $ ,即 $ g({x}_{1}) > g({x}_{2}) $ ,
所以函数 $ g(x) $ 在 $ (0,1) $ 上单调递减.
解析:
10.已知幂函数 $ f(x)=({m}^{2}-4m+4){x}^{5-3m} $ 在 $ (0,+\mathrm{\infty }) $ 上单调递增,二次函数 $ g(x)=a{x}^{2}+2x+c $ .
(1) 求实数 $ m $ 的值.
(2) 当 $ c=1 $ 时, $ \forall x\in [1,2] $ , $ f(x) $ 的图象恒在 $ g(x) $ 图象的下方,求实数 $ a $ 的取值范围.
(3) 若 $ a\leqslant \dfrac{3}{2} $ , $ \forall x\in \boldsymbol{R} $ , $ g(x)\geqslant 0 $ 恒成立,求 $ \dfrac{a+4c-4}{2-a} $ 的最小值.
答案:【解】(1) 因为幂函数 $ f(x)=({m}^{2}-4m+4){x}^{5-3m} $ 在 $ (0,+\mathrm{\infty }) $ 上单调递增,
所以 $ \begin{cases}{m}^{2}-4m+4=1,\\ 5-3m > 0,\end{cases} $ 解得 $ m=1 $ .
(2) 由(1)得 $ f(x)={x}^{2} $ ,
当 $ c=1 $ 时, $ g(x)=a{x}^{2}+2x+1 $ .
因为 $ \forall x\in [1,2] $ , $ f(x) $ 的图象恒在 $ g(x) $ 图象的下方,
所以 $ \forall x\in [1,2] $ ,都有 $ f(x) < g(x) $ ,即 $ {x}^{2} < a{x}^{2}+2x+1 $ ,
分离参数可得 $ a > -\dfrac{1}{{x}^{2}}-\dfrac{2}{x}+1 $ 对 $ \forall x\in [1,2] $ 恒成立,
所以 $ a > {(-\dfrac{1}{{x}^{2}}-\dfrac{2}{x}+1)}_{ \max } $ .
因为 $ x\in [1,2] $ ,所以 $ \dfrac{1}{x}\in [\dfrac{1}{2},1] $ ,
所以 $ -\dfrac{1}{{x}^{2}}-\dfrac{2}{x}+1=-{\left(\dfrac{1}{x}+1\right) ^ {2}}+2\leqslant -\dfrac{9}{4}+2=-\dfrac{1}{4} $ ,
即 $ {(-\dfrac{1}{{x}^{2}}-\dfrac{2}{x}+1)}_{ \max }=-\dfrac{1}{4} $ ,所以 $ a > -\dfrac{1}{4} $ .
所以实数 $ a $ 的取值范围为 $ (-\dfrac{1}{4},+\mathrm{\infty }) $ .
(3) 若 $ a\leqslant \dfrac{3}{2} $ , $ \forall x\in \boldsymbol{R} $ , $ g(x)=a{x}^{2}+2x+c\geqslant 0 $ 恒成立,
则 $ \begin{cases}0 < a\leqslant \dfrac{3}{2},\\ \mathrm{\Delta }=4-4ac\leqslant 0,\end{cases} $ 所以 $ \begin{cases}0 < a\leqslant \dfrac{3}{2},\\ ac\geqslant 1,\end{cases} $
即 $ \begin{cases}0 < a\leqslant \dfrac{3}{2},\\ c\geqslant \dfrac{1}{a},\end{cases} $
所以 $ \dfrac{a+4c-4}{2-a}=\dfrac{-(2-a)+4c-2}{2-a}=\dfrac{4c-2}{2-a}-1\geqslant \dfrac{\dfrac{4}{a}-2}{2-a}-1=\dfrac{2(2-a)}{a(2-a)}-1=\dfrac{2}{a}-1\geqslant \dfrac{2}{\dfrac{3}{2}}-1=\dfrac{1}{3} $ ,
当且仅当 $ a=\dfrac{3}{2} $ , $ c=\dfrac{1}{a}=\dfrac{2}{3} $ 时取等号,
所以 $ \dfrac{a+4c-4}{2-a} $ 的最小值为 $ \dfrac{1}{3} $ .
解析:







