3.4 函数的应用(一)
一、刷基础
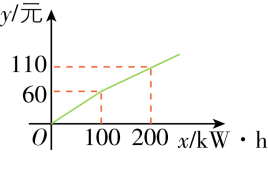
1. 某地供电公司为鼓励小微企业增加夜间时段用电,规定在月度所属夜间计费时段内采用按用电量分段计费的方法来计算电费,夜间月用电量x(单位:kW·h)与相应电费y(单位:元)之间的函数关系如图所示,当夜间月用电量为300 kW·h时,应交电费为 ( )
130元
140元
150元
160元
答案:D
解析:结合题图可知,当x∈(100,+∞)时,y与x之间是一次函数关系,设y=kx+b,x∈(100,+∞),当x=100时,y=60;当x=200时,y=110;
则 $ \begin{cases}60=100k+b,\\ 110=200k+b,\end{cases} $ 解得 $ \begin{cases}k=\dfrac{1}{2},\\ b=10,\end{cases} $ 此时 $ {\rm \mathit{y}=} \dfrac{1}{2} {\rm \mathit{x}+10,\mathit{x}∈(100,+∞)\mathit{.}} $ 所以当x=300时, $ {\rm \mathit{y}=} \dfrac{1}{2} {\rm ×300+10=160\mathit{.}} $ 故选D.
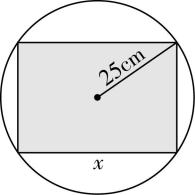
2.如图,把直截面半径为 $ 25\mathrm{c}\mathrm{m} $ 的圆柱形木头锯成直截面为矩形的木料,如果矩形的一边长为 $ x( $ 单位: $ \mathrm{c}\mathrm{m}) $ ,面积为 $ y( $ 单位: $ {\mathrm{c}\mathrm{m}}^{2}) $ ,那么把 $ y $ 表示为 $ x $ 的函数的解析式为( )
A. $ y=x\cdot \sqrt{2500-{x}^{2}} $
B. $ y=x\cdot \sqrt{2500-{x}^{2}} $ , $ 0 < x < 50 $
C. $ y=x\cdot \sqrt{625-{x}^{2}} $
D. $ y=x\cdot \sqrt{625-{x}^{2}} $ , $ 0 < x < 50 $
答案:B
解析:如图,

圆的直径 $ AC=2OC=50\mathrm{c}\mathrm{m} $ ,矩形的边 $ AB=x\mathrm{c}\mathrm{m} $ . $ \because \mathrm{\angle }ABC={90}^{\circ } $ ,
$ \therefore $ 由勾股定理,得 $ BC=\sqrt{2500-{x}^{2}}\mathrm{c}\mathrm{m} $ ,
$ \therefore $ 矩形 $ ABCD $ 的面积 $ y=AB\cdot BC=x\cdot \sqrt{2500-{x}^{2}}{\mathrm{c}\mathrm{m}}^{2} $ ,
又 $ \because 0 < AB < AC=50 $ , $ \therefore 0 < x < 50 $ .故选 $ \mathrm{B} $ .
3.你见过古人眼中的烟花吗?那是朱淑真《元夜》的“火树银花触目红”,是隋炀帝眼中的“灯树千光照,花焰七枝开”.烟花,虽然是没有根的花,是虚幻的花,却在达到最高点时爆裂,用其灿烂的一秒换来人们真心的喝彩.已知某种烟花距地面的高度 $ ℎ $ (单位:米)与时间 $ t $ (单位:秒)之间的关系式为 $ ℎ=-3.6{t}^{2}+28.8t $ ,则烟花在冲击后爆裂的时刻是( )
A.第4秒
B.第5秒
C.第3.5秒
D.第3秒
答案:A
解析:由题意, $ ℎ=-3.6{t}^{2}+28.8t=-3.6(t-4)^{2}+57.6 $ ,
则当 $ t=4 $ 时,烟花达到最高点,即爆裂的时刻是第4秒.故选 $ \mathrm{A} $ .
4.某小型服装厂生产一种风衣,日销货量 $ x $ 件(单位:件) $ (x\in {\boldsymbol{N}}^{\ast }) $ 与货价 $ p $ (单位:元/件)之间的关系为 $ p=160-2x $ ,生产 $ x $ 件所需成本 $ C=100+30x $ (单位:元),当工厂日获利不少于1 000元时,该厂日产量最少生产风衣的件数是 .
解析:由题意,设该厂日获利为 $ y $ 元,则 $ y=(160-2x)x-(100+30x)=-2{x}^{2}+130x-100 $ ,
当工厂日获利不少于1 000元时,即 $ -2{x}^{2}+130x-100\geqslant 1000 $ ,即 $ {x}^{2}-65x+550\leqslant 0⇔(x-10)(x-55)\leqslant 0 $ ,
解得 $ 10\leqslant x\leqslant 55 $ 且 $ x\in {\boldsymbol{N}}^{\ast } $ .
故该厂日产量最少生产风衣的件数是10.
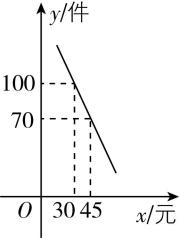
5.某主播在直播平台上销售一款成本为每件24元的商品.经调查发现,该商品每天的销售量 $ y $ (件)与销售单价 $ x $ (元)之间满足一次函数关系,其图象如图所示.
(1) 求该商品每天的销售量 $ y $ 与销售单价 $ x $ 之间的函数关系式.
(2) 若该主播按单价不低于成本价,且不高于50元销售,则销售单价定为多少元时利润最大?最大利润是多少?
(3) 若该主播要使销售该商品每天获得的利润不低于1 280元,则每天的销售量最少应为多少件?
答案:(1) 【解】由题意设 $ y=kx+b $ ,则由题图可知,该函数图象过点 $ (30,100) $ , $ (45,70) $ ,
所以 $ \begin{cases}30k+b=100,\\ 45k+b=70,\end{cases} $ 解得 $ \begin{cases}k=-2,\\ b=160,\end{cases} $
所以 $ y=-2x+160 $ ,
由 $ \begin{cases}x > 0,\\ -2x+160\geqslant 0,\end{cases} $ 解得 $ 0 < x\leqslant 80 $ .
所以该商品每天的销售量 $ y $ 与销售单价 $ x $ 之间的函数关系式是 $ y=-2x+160(0 < x\leqslant 80) $ .
(2) 【解】若该主播按单价不低于成本价24元,且不高于50元销售,
则 $ y=-2x+160(24\leqslant x\leqslant 50) $ ,
则利润 $ z=(-2x+160)(x-24)=-2{x}^{2}+208x-3840(24\leqslant x\leqslant 50) $ ,其图象开口向下,图象的对称轴方程为 $ x=-\dfrac{208}{2×(-2)}=52 $ ,
所以当 $ x=50 $ 时,利润 $ z $ 取得最大值,为 $ -2×{50}^{2}+208×50-3840=1560 $ ,
所以当销售单价为50元时利润最大,最大利润是1 560元.
(3) 【解】由(2)得利润 $ z=-2{x}^{2}+208x-3840 $ ,
又该商品每天获得的利润不低于1 280元,
则 $ -2{x}^{2}+208x-3840\geqslant 1280 $ ,整理得 $ {x}^{2}-104x+2560\leqslant 0 $ ,
即 $ (x-40)(x-64)\leqslant 0 $ ,解得 $ 40\leqslant x\leqslant 64 $ ,
销售量 $ y=-2x+160 $ 是减函数,所以当 $ x=64 $ 时,销售量最小,且最小值为 $ -2×64+160=32 $ 件.
解析:
6.根据统计,一名工人组装第 $ x $ 件产品所用的时间(单位:分)为 $ f (x )=\begin{cases}\dfrac{c}{\sqrt{x}},x < a,\\ \dfrac{c}{\sqrt{a}},x\geqslant a\end{cases} (a $ , $ c $ 为常数 $ ) $ .已知工人组装第4件产品用时30分钟,组装第 $ a $ 件产品用时5分钟,那么 $ c $ 和 $ a $ 的值分别是( )
A.75,25
B.75,16
C.60,144
D.60,16
答案:C
解析:由题意可得 $ a > 4 $ ,
故 $ \begin{cases}\dfrac{c}{\sqrt{4}}=30,\\ \dfrac{c}{\sqrt{a}}=5,\end{cases} $ 则 $ \begin{cases}c=60,\\ a=144.\end{cases} $ 故选 $ \mathrm{C} $ .
7.某公司招聘员工,面试人数按拟录用人数分段计算,计算公式为 $ y=\begin{cases}4x,1\leqslant x < 10,x\in \boldsymbol{N},\\ 2x+10,10\leqslant x < 100,x\in \boldsymbol{N},\\ 1.5x,x\geqslant 100,x\in \boldsymbol{N}.\end{cases} $ 其中, $ x $ 代表拟录用人数, $ y $ 代表面试人数.若面试人数为60,则该公司拟录用人数为( )
A.15
B.40
C.25
D.130
答案:C
解析:令 $ y=60 $ ,若 $ 4x=60 $ ,则 $ x=15 > 10 $ ,不满足题意;
若 $ 2x+10=60 $ ,则 $ x=25 $ ,满足题意;
若 $ 1.5x=60 $ ,则 $ x=40 < 100 $ ,不满足题意.故该公司拟录用25人.
8.某建材商场国庆期间搞促销活动,规定:如果顾客选购物品的总金额不超过1 000元,那么不享受任何折扣优惠;如果顾客选购物品的总金额超过1 000元,那么超过1 000元部分享受一定的折扣优惠,折扣优惠按下表累计计算.
可以享受折扣优惠金额 | 折扣优惠率 |
不超过500元部分 | $ 5\mathrm{\%} $ |
超过500元的部分 | $ 10\mathrm{\%} $ |
若某人在此商场购物获得的折扣优惠金额为40元,则他实际所付金额为 元.
解析:设顾客选购物品的总金额为 $ x $ 元,获得的折扣优惠金额为 $ y $ 元,则当 $ x\in (0,1000] $ 时, $ y=0 $ .
当 $ x\in (1000,1500] $ 时, $ y=(x-1000)×5\mathrm{\%}=0.05x-50 $ ,
令 $ y=40 $ ,得 $ 0.05x-50=40 $ ,解得 $ x=1800 > 1500 $ ,不符合题意.
当 $ x\in (1500,+\mathrm{\infty }) $ 时, $ y=500×0.05+(x-1500)×0.1=25+0.1x-150=0.1x-125 $ ,
令 $ y=40 $ ,得 $ 0.1x-125=40 $ ,解得 $ x=1650 $ ,符合题意,
所以他实际所付金额为 $ 1650-40=1610 $ (元).
9.某公司租地建仓库,已知仓库每月占用费 $ {y}_{1} $ 与仓库到车站的距离成反比,而每月车载货物的运费 $ {y}_{2} $ 与仓库到车站的距离成正比.据测算,如果在距离车站 $ 10\text{ }\mathrm{k}\mathrm{m} $ 处建仓库,这两项费用 $ {y}_{1} $ , $ {y}_{2} $ 分别是2万元和8万元,那么要使这两项费用之和最小,仓库应建在离车站( )
A. $ 5\text{ }\mathrm{k}\mathrm{m} $ 处
B. $ 4\text{ }\mathrm{k}\mathrm{m} $ 处
C. $ 3\text{ }\mathrm{k}\mathrm{m} $ 处
D. $ 2\text{ }\mathrm{k}\mathrm{m} $ 处
答案:A
解析:设仓库到车站的距离为 $ x\text{ }\mathrm{k}\mathrm{m} $ ,由题意可设 $ {y}_{1}=\dfrac{{k}_{1}}{x} $ , $ {y}_{2}={k}_{2}x $ ,其中 $ x > 0 $ .
由当 $ x=10 $ 时,两项费用 $ {y}_{1} $ , $ {y}_{2} $ 分别是2万元和8万元,可得 $ {k}_{1}=20 $ , $ {k}_{2}=\dfrac{4}{5} $ .
故 $ {y}_{1}+{y}_{2}=\dfrac{20}{x}+\dfrac{4}{5}x\geqslant 2\sqrt{\dfrac{20}{x}\cdot \dfrac{4}{5}x}=8 $ ,当且仅当 $ \dfrac{20}{x}=\dfrac{4}{5}x $ ,即 $ x=5 $ 时取等号,故选 $ \mathrm{A} $ .
10.(多选)在固定压力差(压力差为常数)下,当气体通过圆形管道时,其流量 $ v( $ 单位: $ {\mathrm{c}\mathrm{m}}^{3}/\mathrm{s}) $ 与管道的半径 $ r( $ 单位: $ \mathrm{c}\mathrm{m}) $ 的四次方成正比,当气体在半径为 $ 5\mathrm{c}\mathrm{m} $ 的管道中时,流量为 $ 1250{\mathrm{c}\mathrm{m}}^{3}/\mathrm{s} $ ,则( )(多选)
A.当气体在半径为 $ 3\mathrm{c}\mathrm{m} $ 的管道中时,流量为 $ 162{\mathrm{c}\mathrm{m}}^{3}/\mathrm{s} $
B.当气体在半径为 $ 3\mathrm{c}\mathrm{m} $ 的管道中时,流量为 $ 152{\mathrm{c}\mathrm{m}}^{3}/\mathrm{s} $
C.要使得气体流量不小于 $ 512{\mathrm{c}\mathrm{m}}^{3}/\mathrm{s} $ ,管道的半径的最小值为 $ 4\mathrm{c}\mathrm{m} $
D.要使得气体流量不小于 $ 512{\mathrm{c}\mathrm{m}}^{3}/\mathrm{s} $ ,管道的半径的最小值为 $ 3\sqrt{2}\mathrm{c}\mathrm{m} $
答案:AC
解析:依题意可设 $ v=k{r}^{4} $ , $ k $ 为常数.
当气体在半径为 $ 5\mathrm{c}\mathrm{m} $ 的管道中时,流量为 $ 1250{\mathrm{c}\mathrm{m}}^{3}/\mathrm{s} $ ,所以 $ 1250=k×{5}^{4} $ ,解得 $ k=2 $ ,则 $ v=2{r}^{4} $ .当 $ r=3 $ 时, $ v=162 $ ,故 $ \mathrm{A} $ 正确, $ \mathrm{B} $ 错误.
由 $ 2{r}^{4}\geqslant 512 $ ,解得 $ r\geqslant 4 $ ,故 $ \mathrm{C} $ 正确, $ \mathrm{D} $ 错误.故选 $ \mathrm{A}\mathrm{C} $ .
11.某文旅企业准备开发一个新的旅游景区,前期投入200万元,若该景区开业后的第一年接待游客 $ x $ 万人,则需另投入成本 $ P(x) $ 万元,且 $ P(x)=\begin{cases}9,0 < x\leqslant 3,\\ {x}^{2}+24x-60,3 < x < 30,\\ 65x+\dfrac{900}{x}-420,x\geqslant 30,\end{cases} $ 该景区门票价格为64元/人.
(1) 求该景区开业后的第一年的利润 $ R(x) $ (万元)关于人数 $ x $ (万人)的函数关系式.(利润 $ = $ 收入-成本)
(2) 该景区开业后的第一年接待游客为多少人时,获得的利润最大?最大利润为多少?
答案:(1) 【解】该景区的门票收入为 $ 64x $ 万元,则利润
$ R\left(x\right)=\begin{cases}64x-200-9,0 < x\leqslant 3,\\ 64x-200-\left({x}^{2}+24x-60\right),3 < x < 30,\\ 64x-200-\left(65x+\dfrac{900}{x}-420\right),x\geqslant 30,\end{cases} $
即 $ R(x)=\begin{cases}64x-209,0 < x\leqslant 3,\\ -{x}^{2}+40x-140,3 < x < 30,\\ -x-\dfrac{900}{x}+220,x\geqslant 30.\end{cases} $
故该景区开业后的第一年的利润 $ R(x) $ (万元)关于人数 $ x $ (万人)的函数关系式为 $ R(x)=\begin{cases}64x-209,0 < x\leqslant 3,\\ -{x}^{2}+40x-140,3 < x < 30,\\ -x-\dfrac{900}{x}+220,x\geqslant 30.\end{cases} $
(2) 【解】当 $ 0 < x\leqslant 3 $ 时, $ R (x)_{ \max }=R (3 )=-17 $ ;
当 $ 3 < x < 30 $ 时,二次函数图象开口向下,对称轴为直线 $ x=20 $ ,故 $ \mathbf{R} (x)_{ \max }=R (20 )=260 $ ;
当 $ x\geqslant 30 $ 时, $ x+\dfrac{900}{x}\geqslant 2\sqrt{x\cdot \dfrac{900}{x}}=60 $ ,当且仅当 $ x=\dfrac{900}{x} $ ,即 $ x=30 $ 时等号成立,
$ R (x)_{ \max }=R (30 )=-30-\dfrac{900}{30}+220=160 $ .
综上,当该景区开业后的第一年接待游客人数为20万时,获得的利润最大,最大利润为260万元.
解析:
12.(多选)如图①是反映某条公交线路收支差额(即营运所得票价收入与付出成本的差) $ y $ 与乘客量 $ x $ 之间关系的图象.由于目前该条公交线路亏损,公司有关人员提出了两种调整的建议,如图②③所示.
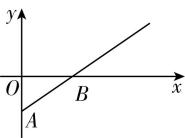
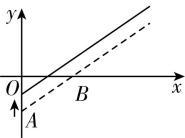
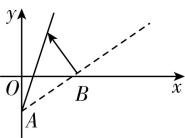
图① 图② 图③
则下列说法中正确的有( )(多选)
A.图②的建议:提高成本,并提高票价
B.图②的建议:降低成本,并保持票价不变
C.图③的建议:提高票价,并保持成本不变
D.图③的建议:提高票价,并降低成本
答案:BC
解析:根据题意和题图②知,两直线平行即票价不变,直线向上平移说明当乘客量为0时,收入是0,但是支出变少了,说明此建议是降低成本并保持票价不变,故 $ \mathrm{A} $ 错误, $ \mathrm{B} $ 正确;由题图③可以看出,当乘客量为0时,支出不变,但是直线的倾斜角变大,即有相同的乘客量时收入变大,即票价提高了,说明此建议是提高票价并保持成本不变,故 $ \mathrm{C} $ 正确, $ \mathrm{D} $ 错误.故选 $ \mathrm{B}\mathrm{C} $ .
二、刷能力
1.一家报刊推销员从报社买进报纸的价格是每份2元,卖出的价格是每份3元,卖不完的还可以以每份0.8元的价格退回报社.在一个月(以30天计算)内有20天每天可卖出400份,其余10天每天只能卖出250份,且每天从报社买进报纸的份数都相同,要使推销员每月所获得的利润最大,则应该每天从报社买进报纸( )
A.215份
B.350份
C.400份
D.250份
答案:C
解析:根据题意,设每天从报社买进 $ x(250\leqslant x\leqslant 400,x\in \boldsymbol{N}) $ 份报纸,每月所获利润为 $ y $ 元,具体情况如表.
| 数量/份 | 单价/元 | 金额/元 |
买进 | $ 30x $ | 2 | $ 60x $ |
卖出 | $ 20x+10×250 $ | 3 | $ 60x+7\text{ }500 $ |
退回 | $ 10(x-250) $ | 0.8 | $ 8x-2\text{ }000 $ |
$ \therefore y=[(60x+7\text{ }500)+(8x-2\text{ }000)]-60x\text{ } $
$ =8x+5\text{ }500(250\leqslant x\leqslant 400,x\in \boldsymbol{N}) $ .
$ \because y=8x+5\text{ }500 $ 在 $ [250,400] $ 上单调递增,
$ \therefore $ 当 $ x=400 $ 时, $ y $ 取得最大值8 700.
即每天从报社买进400份报纸时,每月获得的利润最大,最大利润为8 700元.故选 $ \mathrm{C} $ .
2. 为响应国家退耕还林的号召,某地的耕地面积在最近50年内减少了 $20\mathrm{\%}$ ,如果每年耕地面积减少的百分率相同,设2024年的耕地面积为 $m$ ,则2029年的耕地面积为( )
$ (1-{0.2}^{250})m $
$ (1-{0.8}^{\frac{1}{10}})m $
$ {0.8}^{250}m $
$ {0.8}^{\frac{1}{10}}m $
答案:D
解析:设该地的耕地每年面积减少的百分率为 $x\mathrm{\%}$ ,因为在最近50年内减少了 $20\mathrm{\%}$ ,所以 $(1-x)^{50}=1-20\mathrm{\%}$ ,故 $(1-x)^{5}={0.8}^{\frac{1}{10}}$ .
由题意得2029年的耕地面积为 $m(1-x)^{5}$ ,即 ${0.8}^{\frac{1}{10}}m$ .故选 $\mathrm{D}$ .
3.某企业一个月生产某种商品 $ x $ 万件时的生产成本为 $ C(x)={x}^{2}+4x+16 $ (万元),每件商品售价为28元,假设每月所生产的产品能全部售完.当月所获得的总利润用 $ w(x) $ (万元)表示,用 $ \dfrac{w(x)}{x} $ 表示当月生产商品的单件平均利润,则下列说法正确的是( )
A.当生产12万件时,当月能获得最大总利润144万元
B.当生产12万件时,当月能获得最大总利润160万元
C.当生产4万件时,当月能获得单件平均利润最大为24元
D.当生产4万件时,当月能获得单件平均利润最大为16元
答案:D
解析:由题意可得 $ w(x)=28x-C(x)=-{x}^{2}+24x-16=-{\left(x-12\right) ^ {2}}+128 $ ,
故当 $ x=12 $ 时, $ w(x) $ 取得最大值128.
$ \dfrac{w(x)}{x}=\dfrac{24x-{x}^{2}-16}{x}=24-(x+\dfrac{16}{x})\leqslant 24-2\sqrt{x\cdot \dfrac{16}{x}}=16 $ ,当且仅当 $ x=4 $ 时,等号成立.
因此,当生产12万件时,当月能获得最大总利润128万元,
当生产4万件时,当月能获得单件平均利润最大为16元.故选 $ \mathrm{D} $ .
4.如图,表示一位骑自行车和一位骑摩托车的旅行者在相距 $ 80\mathrm{k}\mathrm{m} $ 的甲、乙两城间从甲城到乙城所行驶的路程与时间之间的函数关系的图象,有人根据函数图象,提出了关于这两个旅行者的如下信息:
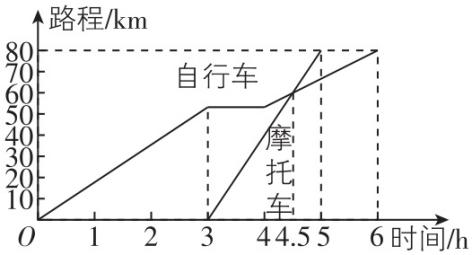
①骑自行车者比骑摩托车者早出发 $ 3\mathrm{h} $ ,晚到 $ 1\mathrm{h} $ ;
②骑自行车者是变速运动,骑摩托车者是匀速运动;
③骑摩托车者在出发 $ 1.5\mathrm{h} $ 后追上了骑自行车者;
④骑摩托车者在出发 $ 1.5\mathrm{h} $ 后与骑自行车者速度一样.
其中,正确信息的序号是 .
解析:看时间轴易知①正确;
骑摩托车者行驶的路程与时间的函数图象是直线,所以是匀速运动,而骑自行车者行驶的路程与时间的函数图象是折线,所以是变速运动,因此②正确;
两个函数图象的交点的横坐标对应着 $ 4.5 $ ,故③正确;
骑自行车者出发 $ 4.5\mathrm{h} $ 后两人相遇,且骑摩托车者先到乙城,所以两者速度不一样,故④错误.
5.某机械厂生产一批零件,受生产能力和技术水平的限制,会产生一些次品,其次品率 $ p $ 与日产量 $ x $ (万件)之间满足关系: $ p=\begin{cases}\dfrac{1}{12-x},0 < x\leqslant m,\\ \dfrac{3}{4},x > m\end{cases} $ (其中 $ m $ 为小于12的正整数).已知每生产1万件合格的零件该厂可以盈利30万元,但每生产1万件次品将亏损10万元,故厂方希望定出合适的日产量使得利润最大.(注:次品率 $ = $ 次品数/生产量,如 $ p=0.1 $ 表示每生产10件产品,有1件为次品,其余为合格品).
(1) 将生产这批零件每天的盈利额 $ y $ (万元)表示为关于日产量 $ x $ (万件)的函数.
(2) 当日产量为多少时,该厂可获得最大利润?
答案:(1) 【解】由题意知 $ y=30\cdot (1-p)x-10\cdot px=(30-40p)x $ ,
当 $ 0 < x\leqslant m $ 时, $ p=\dfrac{1}{12-x} $ ,故 $ y=(30-40\cdot \dfrac{1}{12-x})x=\dfrac{320x-30{x}^{2}}{12-x} $ ,
当 $ x > m $ 时, $ p=\dfrac{3}{4} $ ,故 $ y=(30-40×\dfrac{3}{4})\cdot x=0 $ ,
所以盈利额 $ y $ (万元)与日产量 $ x $ (万件)之间的函数关系为 $ y=\begin{cases}\dfrac{-30{x}^{2}+320x}{12-x},0 < x\leqslant m,\\ 0,x > m.\end{cases} $
(2) 【解】当 $ x > m $ 时,每天的盈利额为0元,则只需求当 $ 0 < x\leqslant m $ 时 $ y $ 的最大值.
设 $ u=12-x $ , $ 0 < x\leqslant m $ ,则 $ x=12-u $ ,且 $ u\in [12-m,12) $ ,
则 $ y=\dfrac{-30 (12-u)^{2}+320 (12-u )}{u}=\dfrac{-30{u}^{2}+400u-480}{u}=-30 (u+\dfrac{16}{u} )+400 $ ,
①当 $ 12-m\leqslant 4 $ ,即 $ 8\leqslant m < 12 $ 时, $ y=-30(u+\dfrac{16}{u})+400\leqslant -30×2\sqrt{u\cdot \dfrac{16}{u}}+400=160 $ ,
当且仅当 $ u=\dfrac{16}{u} $ ,即 $ u=4\in [12-m,12) $ 时, $ y $ 取最大值160,此时 $ x=8 $ .
②当 $ 12-m > 4 $ ,即 $ 0 < m < 8 $ 时,由 $ t=u+\dfrac{16}{u} $ 在 $ [4,+\mathrm{\infty }) $ 上单调递增,
得 $ y=-30(u+\dfrac{16}{u})+400 $ 在 $ [12-m,12) $ 上单调递减,
所以当 $ u=12-m $ ,即 $ x=m $ 时, $ y $ 取最大值.
综上所述,当 $ 0 < m < 8 $ 时,日产量为 $ m $ 万件时,该厂可获最大利润;
当 $ 8\leqslant m < 12 $ 时,日产量为8万件时,该厂可获最大利润.
解析:







