4.2.2 指数函数的图象和性质
一、刷基础
1.已知两个指数函数 $ y={a}^{x} $ , $ y={b}^{x} $ 的部分图象如图所示,则( )

A. $ 0 < b < a < 1 $
B. $ 0 < a < b < 1 $
C. $ a > b > 1 $
D. $ b > a > 1 $
答案:D
解析:由题图可知函数 $ y={a}^{x} $ , $ y={b}^{x} $ 均单调递增,则 $ a > 1 $ , $ b > 1 $ .
当 $ x=-1 $ 时, $ {a}^{-1}=\dfrac{1}{a} > {b}^{-1}=\dfrac{1}{b} $ ,得 $ a < b $ ,所以 $ b > a > 1 $ .故选 $ \mathrm{D} $ .
2.已知函数 $ f(x)=a{(\dfrac{1}{2})}^{|x|}+b $ 的图象过原点,且无限接近直线 $ y=-1 $ ,但又不与该直线相交,则 $ a= $ ( )
A. $ \dfrac{1}{2} $
B. $ -\dfrac{1}{2} $
C.1
D. $ -1 $
答案:C
解析:因为函数 $ f(x)=a{(\dfrac{1}{2})}^{|x|}+b $ 的图象过原点,
所以 $ f(0)=a{\left(\dfrac{1}{2}\right) ^ {0}}+b=a+b=0 $ ,
又因为图象无限接近直线 $ y=-1 $ ,但又不与该直线相交,
所以直线 $ y=-1 $ 是图象的一条渐近线,
所以 $ b=-1 $ ,所以 $ a=1 $ .故选 $ \mathrm{C} $ .
3.要得到函数 $ y={\left(\dfrac{1}{2}\right) ^ {2x}} $ 的图象,只需将函数 $ y={4}^{1-x} $ 的图象( )
A.向左平移1个单位长度
B.向右平移1个单位长度
C.向左平移 $ \dfrac{1}{2} $ 个单位长度
D.向右平移 $ \dfrac{1}{2} $ 个单位长度
答案:A
解析:因为 $ y={\left(\dfrac{1}{2}\right) ^ {2x}}={\left({2}^{-2}\right) ^ {x}}={4}^{-x}={4}^{1-(x+1)} $ ,所以只需将函数 $ y={4}^{1-x} $ 的图象向左平移1个单位长度,即可得到函数 $ y={\left(\dfrac{1}{2}\right) ^ {2x}} $ 的图象.故选 $ \mathrm{A} $ .
4.函数 $ y={a}^{x-2024}-1(a > 0,a\ne 1) $ 的图象恒过的点为 .
解析:对于函数 $ y={a}^{x-2024}-1(a > 0,a\ne 1) $ ,令 $ x-2024=0 $ ,解得 $ x=2024 $ ,此时 $ y={a}^{0}-1=0 $ ,所以函数 $ y={a}^{x-2024}-1(a > 0,a\ne 1) $ 的图象恒过的点为 $ (2024,0) $ .
5.函数 $ f(x)=\dfrac{\sqrt{{2}^{x}-4}}{x-5} $ 的定义域为( )
A. $ (-\mathrm{\infty },2] $
B. $ (-\mathrm{\infty },5)\cup (5,+\mathrm{\infty }) $
C. $ [2,+\mathrm{\infty }) $
D. $ [2,5)\cup (5,+\mathrm{\infty }) $
答案:D
解析:函数 $ f(x)=\dfrac{\sqrt{{2}^{x}-4}}{x-5} $ 的定义域
满足 $ \begin{cases}{2}^{x}-4\geqslant 0,\\ x-5\ne 0,\end{cases} $ 解得 $ x\geqslant 2 $ 且 $ x\ne 5 $ .
6.当 $ x\in [-1,1] $ 时,函数 $ f(x)={3}^{x}-2 $ 的取值范围是( )
A. $ [1,\dfrac{5}{3}] $
B. $ [-1,1] $
C. $ [-\dfrac{5}{3},1] $
D. $ [0,1] $
答案:C
解析:因为指数函数 $ y={3}^{x} $ 在区间 $ [-1,1] $ 上单调递增,所以 $ {3}^{-1}\leqslant {3}^{x}\leqslant {3}^{1} $ ,于是 $ {3}^{-1}-2\leqslant {3}^{x}-2\leqslant {3}^{1}-2 $ ,即 $ -\dfrac{5}{3}\leqslant {3}^{x}-2\leqslant 1 $ ,所以 $ f(x) $ 的取值范围是 $ [-\dfrac{5}{3},1] $ .故选 $ \mathrm{C} $ .
7.下列说法正确的是( )
A. $ {1.5}^{2.3} > {1.5}^{3.2} $
B. $ {0.5}^{-1.2} > {0.5}^{-1.5} $
C. $ {0.8}^{0.9} < {0.9}^{0.8} $
D. $ {1.7}^{0.2} < {0.9}^{3.2} $
答案:C
解析:对于 $ \mathrm{A} $ ,函数 $ y={1.5}^{x} $ 在 $ \boldsymbol{R} $ 上单调递增, $ 2.3 < 3.2 $ ,则 $ {1.5}^{2.3} < {1.5}^{3.2} $ , $ \mathrm{A} $ 错误;
对于 $ \mathrm{B} $ ,函数 $ y={0.5}^{x} $ 在 $ \boldsymbol{R} $ 上单调递减, $ -1.2 > -1.5 $ ,则 $ {0.5}^{-1.2} < {0.5}^{-1.5} $ , $ \mathrm{B} $ 错误;
对于 $ \mathrm{C} $ ,函数 $ y={0.8}^{x} $ 在 $ \boldsymbol{R} $ 上单调递减,函数 $ y={x}^{0.8} $ 在 $ (0,+\mathrm{\infty }) $ 上单调递增,则 $ {0.8}^{0.9} < {0.8}^{0.8} < {0.9}^{0.8} $ , $ \mathrm{C} $ 正确;
对于 $ \mathrm{D} $ , $ {1.7}^{0.2} > {1.7}^{0}=1={0.9}^{0} > {0.9}^{3.2} $ , $ \mathrm{D} $ 错误.故选 $ \mathrm{C} $ .
8.已知函数 $ f(x)=\begin{cases}3x+1,x\leqslant 0,\\ {4}^{x},x > 0,\end{cases} $ 则不等式 $ f(x)+f(x-\dfrac{4}{3}) > 4 $ 的解集为( )
A. $ (\dfrac{3}{2},+\mathrm{\infty }) $
B. $ (1,+\mathrm{\infty }) $
C. $ (\dfrac{1}{2},+\mathrm{\infty }) $
D. $ (\dfrac{1}{3},+\mathrm{\infty }) $
答案:B
解析:当 $ x\leqslant 0 $ 时, $ f(x)+f(x-\dfrac{4}{3})=3x+1+3(x-\dfrac{4}{3})+1=6x-2\leqslant -2 $ ,
则 $ f(x)+f(x-\dfrac{4}{3}) > 4 $ 在 $ x\leqslant 0 $ 时无解;
当 $ 0 < x\leqslant \dfrac{4}{3} $ 时, $ f(x)+f(x-\dfrac{4}{3})={4}^{x}+3(x-\dfrac{4}{3})+1={4}^{x}+3x-3 $ 在 $ \boldsymbol{R} $ 上单调递增,
当 $ x=1 $ 时, $ {4}^{1}+3×1-3=4 $ ,则 $ f(x)+f(x-\dfrac{4}{3}) > 4 $ 的解集为 $ (1,\dfrac{4}{3}] $ ;
当 $ x > \dfrac{4}{3} $ 时, $ f(x)+f(x-\dfrac{4}{3})={4}^{x}+{4}^{x-\frac{4}{3}} > {4}^{\frac{4}{3}}+{4}^{0} > 4 $ ,
则 $ f(x)+f(x-\dfrac{4}{3}) > 4 $ 在 $ x > \dfrac{4}{3} $ 时恒成立.
综上,不等式 $ f(x)+f(x-\dfrac{4}{3}) > 4 $ 的解集为 $ (1,+\mathrm{\infty }) $ .故选 $ \mathrm{B} $ .
9.设 $ a $ 为实数,若关于 $ x $ 的方程 $ {4}^{x}+{2}^{x+1}+a=0 $ 有实数解,则 $ a $ 的取值范围是( )
A. $ (0,+\mathrm{\infty }) $
B. $ [0,+\mathrm{\infty }) $
C. $ (-\mathrm{\infty },0) $
D. $ (-\mathrm{\infty },0] $
答案:C
解析:因为 $ {4}^{x}+{2}^{x+1}+a=0 $ ,所以 $ -a={4}^{x}+{2}^{x+1}={\left({2}^{x}\right) ^ {2}}+2×{2}^{x} $ ,
令 $ t={2}^{x}(t > 0) $ ,则 $ -a={t}^{2}+2t(t > 0) $ ,
要使方程 $ {4}^{x}+{2}^{x+1}+a=0 $ 有实数解只需直线 $ y=-a $ 与 $ f(t)={t}^{2}+2t(t > 0) $ 的图象有交点即可.
设 $ f(t)={t}^{2}+2t={\left(t+1\right) ^ {2}}-1 $ ,当 $ t > 0 $ 时, $ f(t) $ 单调递增,所以 $ f(t) > f(0)=0 $ ,
则 $ -a > 0 $ ,即 $ a < 0 $ ,
故 $ a $ 的取值范围是 $ (-\mathrm{\infty },0) $ .故选 $ \mathrm{C} $ .
10.若不等式 $ {3}^{{x}^{2}-2ax} > {\left(\dfrac{1}{3}\right) ^ {x+1}} $ 对一切实数 $ x $ 恒成立,则实数 $ a $ 的取值范围为( )
A. $ (-\dfrac{1}{2},\dfrac{3}{2}) $
B. $ [-\dfrac{1}{2},\dfrac{3}{2}] $
C. $ (-\mathrm{\infty },-\dfrac{1}{2})\cup (\dfrac{3}{2},+\mathrm{\infty }) $
D. $ (-\mathrm{\infty },-\dfrac{1}{2}]\cup [\dfrac{3}{2},+\mathrm{\infty }) $
答案:A
解析:因为不等式 $ {3}^{{x}^{2}-2ax} > {\left(\dfrac{1}{3}\right) ^ {x+1}} $ 对一切实数 $ x $ 恒成立,所以 $ {3}^{{x}^{2}-2ax} > {3}^{-x-1} $ 对一切实数 $ x $ 恒成立.
又因为 $ y={3}^{x} $ 为 $ \boldsymbol{R} $ 上的增函数,所以 $ {x}^{2}-2ax > -x-1 $ 对一切实数 $ x $ 恒成立,所以 $ {x}^{2}+(1-2a)x+1 > 0 $ 对一切实数 $ x $ 恒成立,故 $ \Delta ={\left(1-2a\right) ^ {2}}-4 < 0 $ ,解得 $ -\dfrac{1}{2} < a < \dfrac{3}{2} $ ,故选 $ \mathrm{A} $ .
11.函数 $ y={2}^{\left|x-1\right|} $ 在区间 $ (k-1,k+1) $ 内不单调,则实数 $ k $ 的取值范围是 .
解析:令 $ t=\left|x-1\right| $ ,则 $ y={2}^{t} $ .因为 $ y={2}^{\left|x-1\right|} $ 在区间 $ (k-1,k+1) $ 内不单调,所以 $ t=\left|x-1\right| $ 在区间 $ (k-1,k+1) $ 内不单调.又因为 $ t=\left|x-1\right| $ 在 $ (-\mathrm{\infty },1) $ 上单调递减,在 $ [1,+\mathrm{\infty }) $ 上单调递增,所以 $ k-1 < 1 < k+1 $ ,解得 $ 0 < k < 2 $ .
12.已知函数 $ f(x)=\dfrac{{4}^{x}+1}{{4}^{x}-a} $ 为奇函数.
(1) 求 $ a $ 的值;
(2) 解不等式 $ f(x) > 3 $ ;
(3) 求 $ f(x) $ 的值域.
答案:(1) 【解】由题意可得 $ f(-x)=\dfrac{{4}^{-x}+1}{{4}^{-x}-a}=\dfrac{1+{4}^{x}}{1-a\cdot {4}^{x}}=-f(x)=-\dfrac{{4}^{x}+1}{{4}^{x}-a} $ ,
所以 $ 1-a\cdot {4}^{x}=a-{4}^{x}⇒1-a=(a-1)\cdot {4}^{x} $ ,
因为 $ {4}^{x}\ne 0 $ ,所以 $ a=1 $ .
经验证当 $ a=1 $ 时, $ f(x) $ 为奇函数.
(2) 不等式 $ f(x) > 3 $ 等价于 $ \dfrac{{4}^{x}+1}{{4}^{x}-1} > 3 $ ,则 $ \dfrac{{4}^{x}+1}{{4}^{x}-1}-3 > 0 $ ,化简得 $ \dfrac{4-2\cdot {4}^{x}}{{4}^{x}-1} > 0⇒(2-{4}^{x})\cdot ({4}^{x}-1) > 0 $ ,
所以 $ 1 < {4}^{x} < 2 $ ,所以 $ 0 < x < \dfrac{1}{2} $ ,
所以原不等式的解集为 $ (0,\dfrac{1}{2}) $ .
(3) 令 $ y=\dfrac{{4}^{x}+1}{{4}^{x}-1} $ ,则 $ y\cdot ({4}^{x}-1)={4}^{x}+1 $ ,整理得 $ (y-1)\cdot {4}^{x}=y+1 $ ,
即 $ {4}^{x}=\dfrac{y+1}{y-1}(y\ne 1) $ .
又 $ {4}^{x} > 0 $ ,所以 $ \dfrac{y+1}{y-1} > 0 $ ,解得 $ y > 1 $ 或 $ y < -1 $ ,
所以 $ f(x) $ 的值域为 $ (-\mathrm{\infty },-1)\cup (1,+\mathrm{\infty }) $ .
解析:
13.函数 $ y={3}^{|x|}-2 $ 的值域是( )
A. $ \boldsymbol{R} $
B. $ (-2,+\mathrm{\infty }) $
C. $ [-2,+\mathrm{\infty }) $
D. $ [-1,+\mathrm{\infty }) $
答案:D
解析:令 $ |x|=t $ , $ t\geqslant 0 $ ,则 $ {3}^{t}\geqslant 1 $ , $ y={3}^{t}-2\geqslant -1 $ ,所以 $ y\geqslant -1 $ .故选 $ \mathrm{D} $ .
14.函数 $ y=\sqrt{4-{2}^{x}}-1 $ 的值域为( )
A. $ [1,+\mathrm{\infty }) $
B. $ (-1,1) $
C. $ [-1,+\mathrm{\infty }) $
D. $ [-1,1) $
答案:D
解析: $ \because {2}^{x} > 0 $ , $ \therefore 4-{2}^{x} < 4 $ .又 $ \because 4-{2}^{x}\geqslant 0 $ , $ \therefore 0\leqslant 4-{2}^{x} < 4 $ .令 $ t=4-{2}^{x} $ ,则 $ t\in [0,4) $ , $ \therefore \sqrt{t}\in [0,2) $ , $ \therefore y\in [-1,1) $ ,即函数的值域是 $ [-1,1) $ .故选 $ \mathrm{D} $ .
15.若函数 $ y={a}^{x}(a > 0 $ ,且 $ a\ne 1) $ 在 $ [1,2] $ 上的最大值与最小值的差为 $ \dfrac{a}{2} $ ,则实数 $ a $ 的值为( )
A. $ \dfrac{1}{2} $
B. $ \dfrac{3}{2} $
C. $ \dfrac{2}{3} $ 或2
D. $ \dfrac{1}{2} $ 或 $ \dfrac{3}{2} $
答案:D
解析:当 $ 0 < a < 1 $ 时, $ y={a}^{x} $ 在 $ [1,2] $ 上单调递减,所以 $ a-{a}^{2}=\dfrac{a}{2} $ ,解得 $ a=\dfrac{1}{2} $ 或 $ a=0 $ (舍去);
当 $ a > 1 $ 时, $ y={a}^{x} $ 在 $ [1,2] $ 上单调递增,所以 $ {a}^{2}-a=\dfrac{a}{2} $ ,解得 $ a=\dfrac{3}{2} $ 或 $ a=0 $ (舍去).
综上所述, $ a=\dfrac{1}{2} $ 或 $ a=\dfrac{3}{2} $ .故选 $ \mathrm{D} $ .
16.已知函数 $ f (x )={a}^{x} (a > 0 $ ,且 $ a\ne 1) $ 在 $ [-1,1] $ 上恒有 $ f(x) < 2 $ ,则实数 $ a $ 的取值范围是 .
答案: $ (\dfrac{1}{2},1)\cup (1,2) $
解析:当 $ a > 1 $ 时, $ f(x) $ 在 $ [-1,1] $ 上单调递增.因为函数 $ f(x) $ 在 $ [-1,1] $ 上恒有 $ f(x) < 2 $ ,所以 $ f(1) < 2 $ ,所以 $ a < 2 $ ,所以 $ 1 < a < 2 $ .
当 $ 0 < a < 1 $ 时, $ f(x) $ 在 $ [-1,1] $ 上单调递减.因为函数 $ f(x) $ 在 $ [-1,1] $ 上恒有 $ f(x) < 2 $ ,所以 $ f(-1) < 2 $ ,所以 $ \dfrac{1}{a} < 2 $ ,即 $ a > \dfrac{1}{2} $ ,所以 $ \dfrac{1}{2} < a < 1 $ .
综上所述,实数 $ a $ 的取值范围是 $ (\dfrac{1}{2},1)\cup (1,2) $ .
17.函数 $ y={4}^{x}+{2}^{x+1}+1 $ 的值域为( )
A. $ (0,+\mathrm{\infty }) $
B. $ (1,+\mathrm{\infty }) $
C. $ [1,+\mathrm{\infty }) $
D. $ \boldsymbol{R} $
答案:B
解析:设 $ t={2}^{x} $ ,则 $ t > 0 $ ,所以 $ y={t}^{2}+2t+1={\left(t+1\right) ^ {2}} $ 在 $ (0,+\mathrm{\infty }) $ 上单调递增,所以 $ y > 1 $ ,所以函数 $ y={4}^{x}+{2}^{x+1}+1 $ 的值域为 $ (1,+\mathrm{\infty }) $ ,故选 $ \mathrm{B} $ .
18.设函数 $ f(x)={3}^{x(x-a)} $ 在区间 $ (0,\dfrac{3}{2}) $ 上单调递减,则实数 $ a $ 的取值范围是( )
A. $ (-\mathrm{\infty },-1) $
B. $ [-3,0) $
C. $ (0,1] $
D. $ [3,+\mathrm{\infty }) $
答案:D
解析:因为函数 $ y={3}^{x} $ 在 $ \boldsymbol{R} $ 上单调递增,而函数 $ f(x)={3}^{x(x-a)} $ 在区间 $ (0,\dfrac{3}{2}) $ 上单调递减,则函数 $ y=x(x-a)={\left(x-\dfrac{a}{2}\right) ^ {2}}-\dfrac{{a}^{2}}{4} $ 在区间 $ (0,\dfrac{3}{2}) $ 上单调递减,
因此 $ \dfrac{a}{2}\geqslant \dfrac{3}{2} $ ,解得 $ a\geqslant 3 $ ,所以实数 $ a $ 的取值范围是 $ [3,+\mathrm{\infty }) $ .故选 $ \mathrm{D} $ .
19.已知函数 $ f(x)=\dfrac{{2}^{x}-1}{{2}^{x}+1} $ ,则( )(多选)
A.函数 $ f(x) $ 的图象关于原点对称
B.函数 $ f(x) $ 的图象关于 $ y $ 轴对称
C.函数 $ f(x) $ 的值域为 $ (-1,1) $
D.函数 $ f(x) $ 是减函数
答案:AC
解析: $ f(x) $ 的定义域为 $ \boldsymbol{R} $ , $ f(x)=\dfrac{{2}^{x}-1}{{2}^{x}+1} $ ,则 $ f(-x)=\dfrac{{2}^{-x}-1}{{2}^{-x}+1}=-\dfrac{{2}^{x}-1}{{2}^{x}+1}=-f(x) $ ,
所以 $ f(x) $ 为奇函数, $ f(x) $ 的图象关于原点对称, $ \mathrm{A} $ 正确, $ \mathrm{B} $ 错误;
$ f(x)=\dfrac{{2}^{x}-1}{{2}^{x}+1}=1-\dfrac{2}{{2}^{x}+1} $ ,因为 $ {2}^{x}+1 > 1 $ ,所以 $ 0 < \dfrac{1}{{2}^{x}+1} < 1 $ ,所以 $ 0 < \dfrac{2}{{2}^{x}+1} < 2 $ ,所以 $ -1 < 1-\dfrac{2}{{2}^{x}+1} < 1 $ ,故 $ f(x) $ 的值域为 $ (-1,1) $ , $ \mathrm{C} $ 正确;
设 $ {x}_{2} > {x}_{1} $ ,则 $ f({x}_{2})-f({x}_{1})=(1-\dfrac{2}{{2}^{{x}_{2}}+1})-(1-\dfrac{2}{{2}^{{x}_{1}}+1})=\dfrac{2}{{2}^{{x}_{1}}+1}-\dfrac{2}{{2}^{{x}_{2}}+1}=\dfrac{2({2}^{{x}_{2}}-{2}^{{x}_{1}})}{({2}^{{x}_{1}}+1)({2}^{{x}_{2}}+1)} $ ,因为 $ {x}_{2} > {x}_{1} $ ,所以 $ {2}^{{x}_{2}}-{2}^{{x}_{1}} > 0 $ , $ {2}^{{x}_{1}}+1 > 0 $ , $ {2}^{{x}_{2}}+1 > 0 $ ,所以 $ f({x}_{2})-f({x}_{1}) > 0 $ ,即 $ f({x}_{2}) > f({x}_{1}) $ ,所以函数 $ f(x) $ 是增函数,故 $ \mathrm{D} $ 错误.
故选 $ \mathrm{A}\mathrm{C} $ .
20.已知不等式 $ {9}^{x}-4\cdot {3}^{x}+3\leqslant 0 $ 的解集为集合 $ A $ ,函数 $ f(x)={4}^{-x}-3\cdot {2}^{-x-1}+1 $ , $ x\in A $ .
(1)求集合 $ A $ ;
(2)求函数 $ f(x) $ 的值域.
解析:(1)由 $ {9}^{x}-4×{3}^{x}+3\leqslant 0 $ ,得 $ {\left({3}^{x}\right) ^ {2}}-4×{3}^{x}+3\leqslant 0 $ ,即 $ ({3}^{x}-1)\cdot ({3}^{x}-3)\leqslant 0 $ ,即 $ 1\leqslant {3}^{x}\leqslant 3 $ ,解得 $ 0\leqslant x\leqslant 1 $ ,故集合 $ A={x|0\leqslant x\leqslant 1} $ .
(2) $ f(x)={4}^{-x}-3×{2}^{-x-1}+1={\left({2}^{-x}\right) ^ {2}}-\dfrac{3}{2}×{2}^{-x}+1 $ ,令 $ t={2}^{-x} $ ,则 $ f(x) $ 可化为 $ g(t)={t}^{2}-\dfrac{3}{2}t+1 $ .
$ \because x\in [0,1] $ , $ \therefore t\in [\dfrac{1}{2},1] $ ,而函数 $ g(t)={t}^{2}-\dfrac{3}{2}t+1 $ 的图象的对称轴为直线 $ t=\dfrac{3}{4}\in [\dfrac{1}{2},1] $ , $ \therefore g(t)={t}^{2}-\dfrac{3}{2}t+1 $ 在区间 $ [\dfrac{1}{2},\dfrac{3}{4}) $ 上单调递减,在区间 $ (\dfrac{3}{4},1] $ 上单调递增.故 $ g(t) $ 在 $ [\dfrac{1}{2},1] $ 上的最大值为 $ g(\dfrac{1}{2})=g(1)=\dfrac{1}{2} $ ,最小值为 $ g(\dfrac{3}{4})=\dfrac{9}{16}-\dfrac{3}{2}×\dfrac{3}{4}+1=\dfrac{7}{16} $ ,故函数 $ f(x) $ 的值域为 $ [\dfrac{7}{16},\dfrac{1}{2}] $ .
二、刷提升
1.如图所示,若 $ 0 < a < 1 $ ,函数 $ y={a}^{x} $ 与 $ y=x+a $ 的图象可能是( )
A.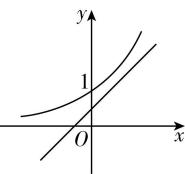
B.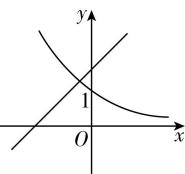
C.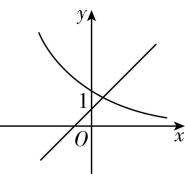
D.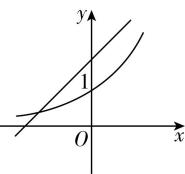
答案:C
解析:因为 $ 0 < a < 1 $ ,所以指数函数 $ y={a}^{x} $ 在 $ \boldsymbol{R} $ 上单调递减,所以排除 $ \mathrm{A} $ 和 $ \mathrm{D} $ ;
对于 $ y=x+a $ ,当 $ x=0 $ 时, $ y=a $ ,所以 $ y=x+a $ 的图象过点 $ (0,a) $ ,因为 $ 0 < a < 1 $ ,所以 $ \mathrm{B} $ 错误, $ \mathrm{C} $ 正确.故选 $ \mathrm{C} $ .
2.设 $ a={(\dfrac{3}{5})}^{\frac{2}{5}} $ , $ b={\left(\dfrac{2}{5}\right) ^ {2}} $ , $ c={(\dfrac{5}{3})}^{\frac{1}{2}} $ , $ d={(\dfrac{2}{5})}^{\frac{2}{5}} $ ,则 $ a $ , $ b $ , $ c $ , $ d $ 的大小关系是( )
A. $ a > c > b > d $
B. $ c > a > d > b $
C. $ c > a > b > d $
D. $ c > d > a > b $
答案:B
解析:因为 $ y={\left(\dfrac{5}{3}\right) ^ {x}} $ 是增函数,所以 $ {(\dfrac{5}{3})}^{\frac{1}{2}} > {\left(\dfrac{5}{3}\right) ^ {0}}=1 $ ,因为 $ y={\left(\dfrac{3}{5}\right) ^ {x}} $ 是减函数,所以 $ {(\dfrac{3}{5})}^{\frac{2}{5}} < {\left(\dfrac{3}{5}\right) ^ {0}}=1 $ ,
故 $ c={(\dfrac{5}{3})}^{\frac{1}{2}} > 1 > {(\dfrac{3}{5})}^{\frac{2}{5}}=a $ ,
又函数 $ y={x}^{\frac{2}{5}} $ 在第一象限内为增函数,故 $ a={(\dfrac{3}{5})}^{\frac{2}{5}} > {(\dfrac{2}{5})}^{\frac{2}{5}}=d $ ,
又 $ y={\left(\dfrac{2}{5}\right) ^ {x}} $ 为减函数,故 $ d={(\dfrac{2}{5})}^{\frac{2}{5}} > {\left(\dfrac{2}{5}\right) ^ {2}}=b $ ,
综上可得 $ c > a > d > b $ .故选 $ \mathrm{B} $ .
3.函数 $ f(x)={(\dfrac{1}{3})}^{|x-2|} $ 的单调递减区间是( )
A. $ (-\mathrm{\infty },2] $
B. $ [2,+\mathrm{\infty }) $
C. $ [-2,+\mathrm{\infty }) $
D. $ (-\mathrm{\infty },-2] $
答案:B
解析:将原函数看成复合函数 $ y={\left(\dfrac{1}{3}\right) ^ {u}} $ , $ u=|x-2| $ ,因为 $ y={\left(\dfrac{1}{3}\right) ^ {u}} $ 是关于 $ u $ 的减函数,且 $ u=|x-2| $ 在 $ [2,+\mathrm{\infty }) $ 上单调递增,在 $ (-\mathrm{\infty },2] $ 上单调递减,所以由复合函数的性质知 $ f(x) $ 的单调递减区间是 $ [2,+\mathrm{\infty }) $ .
4.若直线 $ y=3a $ 与函数 $ y= |{a}^{x}-1 | (a > 0 $ ,且 $ a\ne 1) $ 的图象有两个公共点,则 $ a $ 可以是( )
A.2
B. $ \dfrac{1}{3} $
C. $ \dfrac{1}{4} $
D. $ \dfrac{2}{3} $
答案:C
解析:当 $ 0 < a < 1 $ 时, $ y=\left|{a}^{x}-1\right| $ 的图象如图①所示,由已知得 $ 0 < 3a < 1 $ , $ \therefore 0 < a < \dfrac{1}{3} $ ;
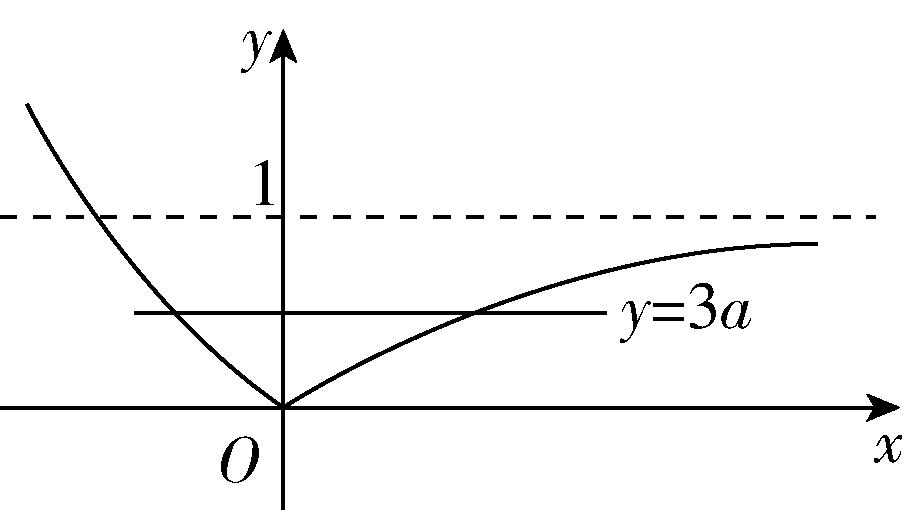
图①
当 $ a > 1 $ 时, $ y=\left|{a}^{x}-1\right| $ 的图象如图②所示,由已知可得 $ 0 < 3a < 1 $ , $ \therefore 0 < a < \dfrac{1}{3} $ ,结合 $ a > 1 $ 可得 $ a $ 无解.
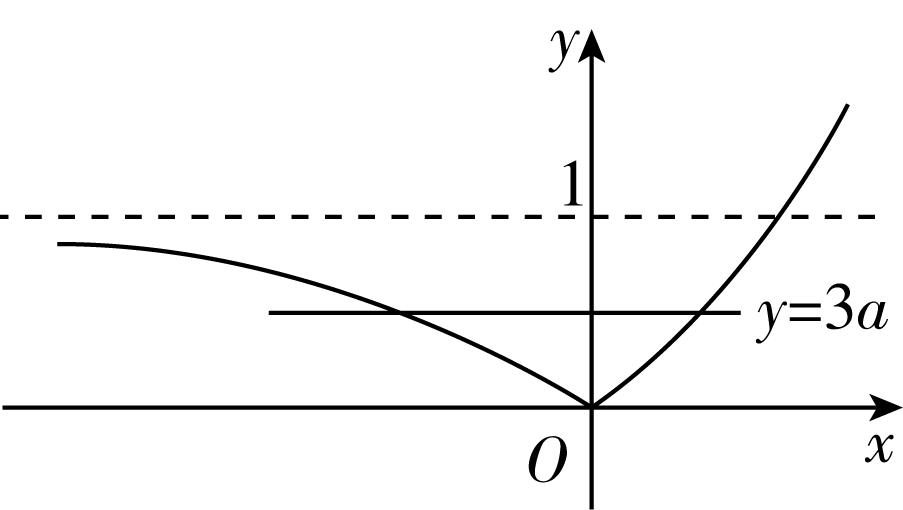
图②
综上可知, $ a $ 的取值范围为 $ (0,\dfrac{1}{3}) $ .故选 $ \mathrm{C} $ .
5.若函数 $ f (x )=\begin{cases}a+{a}^{x},x\geqslant 0,\\ 3+ (a-1 )x,x < 0\end{cases} (a > 0 $ 且 $ a\ne 1) $ 满足对任意 $ {x}_{1}\ne {x}_{2} $ ,都有 $ \dfrac{f({x}_{1})-f({x}_{2})}{{x}_{1}-{x}_{2}} > 0 $ 成立,则 $ a $ 的值可以是( )
A. $ \dfrac{1}{3} $
B. $ \dfrac{2}{3} $
C. $ \sqrt{2} $
D.2
答案:D
解析:因为对任意 $ {x}_{1}\ne {x}_{2} $ ,都有 $ \dfrac{f({x}_{1})-f({x}_{2})}{{x}_{1}-{x}_{2}} > 0 $ 成立,
所以 $ f(x) $ 在 $ (-\mathrm{\infty },+\mathrm{\infty }) $ 上单调递增,
所以 $ \begin{cases}a > 1,\\ a-1 > 0,\\ a+{a}^{0}\geqslant 3+(a-1)×0,\end{cases} $ 解得 $ a\geqslant 2 $ .故选 $ \mathrm{D} $ .
6.(多选)已知函数 $ f(x)={\mathrm{e}}^{-x2+2ax} $ ,其中 $ \mathrm{e} {\rm =2.71828} $ …,则( )(多选)
A.当 $ a=0 $ 时, $ f(x) $ 为偶函数
B. $ f(x) $ 既有最大值又有最小值
C. $ f(x) $ 在 $ (-\mathrm{\infty },a] $ 上单调递增
D. $ f(x) $ 的图象恒过定点
答案:ACD
解析:当 $ a=0 $ 时, $ f(x)={\mathrm{e}}^{-{x}^{2}} $ ,定义域为 $ \boldsymbol{R} $ ,因为 $ f (-x )={\mathrm{e}}^{- (-x)^{2}}={\mathrm{e}}^{-{x}^{2}}=f (x ) $ ,所以 $ f(x) $ 为偶函数, $ \mathrm{A} $ 正确;
因为 $ y=-{x}^{2}+2ax=-{\left(x-a\right) ^ {2}}+{a}^{2}\leqslant {a}^{2} $ ,所以 $ 0 < f(x)={\mathrm{e}}^{-{x}^{2}+2ax}\leqslant {\mathrm{e}}^{{a}^{2}} $ ,则 $ f(x) $ 有最大值,没有最小值, $ \mathrm{B} $ 错误;
因为 $ y=-{x}^{2}+2ax $ 在 $ (-\mathrm{\infty },a] $ 上单调递增,在 $ (a,+\mathrm{\infty }) $ 上单调递减,
又 $ y={\mathrm{e}}^{x} $ 在 $ \boldsymbol{R} $ 上单调递增,
所以 $ f(x) $ 在 $ (-\mathrm{\infty },a] $ 上单调递增,在 $ (a,+\mathrm{\infty }) $ 上单调递减, $ \mathrm{C} $ 正确;
当 $ x=0 $ 时, $ f(0)={\mathrm{e}}^{0}=1 $ ,所以 $ f(x) $ 的图象恒过定点 $ (0,1) $ , $ \mathrm{D} $ 正确.故选 $ \mathrm{A}\mathrm{C}\mathrm{D} $ .
7.已知函数 $ f(x)=\dfrac{1}{{3}^{x}}-{3}^{x}-2x+4 $ ,若 $ f(a-6)+f({a}^{2}) > 8 $ ,则实数 $ a $ 的取值范围是( )
A. $ (2,+\mathrm{\infty }) $
B. $ (-3,2) $
C. $ (-\mathrm{\infty },-3) $
D. $ (-\mathrm{\infty },-3)\cup (2,+\mathrm{\infty }) $
答案:B
解析:令 $ g(x)=f(x)-4=\dfrac{1}{{3}^{x}}-{3}^{x}-2x $ ,定义域为 $ \boldsymbol{R} $ ,则 $ g(-x)=\dfrac{1}{{3}^{-x}}-{3}^{-x}+2x={3}^{x}-\dfrac{1}{{3}^{x}}+2x=-g(x) $ ,所以 $ g(x) $ 为奇函数.
不等式 $ f(a-6)+f({a}^{2}) > 8 $ ,
等价于 $ f(a-6)-4 > -(f({a}^{2})-4) $ ,
即 $ g(a-6) > -g({a}^{2}) $ .
因为 $ g(x) $ 为奇函数,所以 $ g(a-6) > g(-{a}^{2}) $ .
因为 $ y=\dfrac{1}{{3}^{x}} $ , $ y=-{3}^{x} $ , $ y=-2x $ 均为减函数,所以 $ g(x) $ 为减函数,
则 $ a-6 < -{a}^{2} $ ,解得 $ -3 < a < 2 $ .故选 $ \mathrm{B} $ .
8.若函数 $ y={a}^{2x}+{a}^{x}+1(a > 0,a\ne 1) $ 在区间 $ [-1,1] $ 上的最大值是13,则实数 $ a $ 的值为 .
解析:设 $ t={a}^{x} $ ,则函数等价于 $ y={t}^{2}+t+1={\left(t+\dfrac{1}{2}\right) ^ {2}}+\dfrac{3}{4} $ ,图象的对称轴为直线 $ t=-\dfrac{1}{2} $ ,该二次函数在 $ [-\dfrac{1}{2} $ , $ +\mathrm{\infty }) $ 上单调递增.
①若 $ a > 1 $ ,由 $ x\in [-1,1] $ ,得 $ t={a}^{x}\in [\dfrac{1}{a},a] $ ,且 $ t > 0 $ ,故当 $ t=a $ ,即 $ x=1 $ 时, $ {y}_{ \max }={a}^{2}+a+1=13 $ ,解得 $ a=3 $ 或 $ a=-4 $ (舍去).
②若 $ 0 < a < 1 $ ,由 $ x\in [-1,1] $ ,可得 $ t={a}^{x}\in [a,\dfrac{1}{a}] $ ,且 $ t > 0 $ ,故当 $ t=\dfrac{1}{a} $ ,即 $ x=-1 $ 时, $ {y}_{ \max }={\left(\dfrac{1}{a}\right) ^ {2}}+\dfrac{1}{a}+1=13 $ , $ \therefore a=\dfrac{1}{3} $ 或 $ a=-\dfrac{1}{4} $ (舍去).
综上可得, $ a=3 $ 或 $ \dfrac{1}{3} $ .
9.已知函数 $ f(x)=\dfrac{{2}^{x}-1}{{2}^{x}+1}{x}^{2}+x+1 $ ,则 $ f(-1012)+f(-1011)+\cdots +f(-1)+f(0)+f(1)+\cdots +f(1011)+f(1012) $ 的值为 .
解析:因为函数 $ f(x)=\dfrac{{2}^{x}-1}{{2}^{x}+1}{x}^{2}+x+1 $ 的定义域为 $ \boldsymbol{R} $ ,
所以 $ f(-x)+f(x)=\dfrac{{2}^{-x}-1}{{2}^{-x}+1}{x}^{2}-x+1+\dfrac{{2}^{x}-1}{{2}^{x}+1}{x}^{2}+x+1=\dfrac{1-{2}^{x}}{{2}^{x}+1}{x}^{2}+\dfrac{{2}^{x}-1}{{2}^{x}+1}{x}^{2}+2=2 $ ,
所以 $ f(-1012)+f(-1011)+\cdots +f(-1)+f(0)+f(1)+\cdots +f(1011)+f(1012)=2×1012+1=2025 $ .
10.已知定义在 $ \boldsymbol{R} $ 上的函数 $ f(x)=m\cdot {4}^{x}-{2}^{x+1}-m(m\in \boldsymbol{R}) $ .
(1) 当 $ m=1 $ 时,求 $ f(x) $ 的值域;
(2) 若函数 $ f(x) $ 在 $ (1,+\mathrm{\infty }) $ 上单调递增,求实数 $ m $ 的取值范围;
(3) 若函数 $ y=g(x) $ 的定义域内存在 $ {x}_{0} $ ,使得 $ g(a+{x}_{0})+g(a-{x}_{0})=2b $ 成立,则称 $ g(x) $ 为局部对称函数,其中 $ (a,b) $ 为函数 $ g(x) $ 的局部对称点,若 $ (1,0) $ 是函数 $ y=f(x) $ 的局部对称点,求实数 $ m $ 的取值范围.
答案:【解】(1) 当 $ m=1 $ 时, $ f(x)={4}^{x}-{2}^{x+1}-1 $ ,
令 $ {2}^{x}=s > 0 $ ,则 $ f(x)={4}^{x}-{2}^{x+1}-1 $ 可转化为 $ y={s}^{2}-2s-1(s > 0) $ ,即 $ y={\left(s-1\right) ^ {2}}-2\geqslant -2 $ , $ \therefore f(x) $ 的值域为 $ [-2,+\mathrm{\infty }) $ .
(2) 令 $ k={2}^{x} $ , $ \because x > 1 $ , $ \therefore k > 2 $ ,则 $ f(x) $ 可转化为 $ y=m{k}^{2}-2k-m(k > 2) $ .
$ \because k={2}^{x} $ 在 $ (1,+\mathrm{\infty }) $ 上单调递增,
$ \therefore $ 要使 $ f(x) $ 在 $ (1,+\mathrm{\infty }) $ 上单调递增,
只需 $ y=m{k}^{2}-2k-m $ 在 $ (2,+\mathrm{\infty }) $ 上单调递增即可.
①当 $ m=0 $ 时, $ y=-2k $ 在 $ (2,+\mathrm{\infty }) $ 上单调递减,不符合题意;
②当 $ m < 0 $ 时, $ y=m{k}^{2}-2k-m $ 的图象开口向下,不符合题意;
③当 $ m > 0 $ 时,需满足 $ \begin{cases}m > 0,\\ \dfrac{1}{m}\leqslant 2,\end{cases} $ 解得 $ m\geqslant \dfrac{1}{2} $ .
综上,实数 $ m $ 的取值范围是 $ [\dfrac{1}{2},+\mathrm{\infty }) $ .
(3) 由 $ (1,0) $ 是函数 $ y=f(x) $ 的局部对称点,得 $ \exists x\in \boldsymbol{R} $ ,使得 $ f(1+x)+f(1-x)=0 $ ,
代入整理得 $ 2m({4}^{x}+{4}^{-x})-2({2}^{x}+{2}^{-x})-m=0 $ .①
令 $ t={2}^{x}+{2}^{-x} $ ,则 $ t\geqslant 2 $ ,当且仅当 $ x=0 $ 时取等号,则 $ {4}^{x}+{4}^{-x}={\left({2}^{x}+{2}^{-x}\right) ^ {2}}-2={t}^{2}-2 $ ,
代入①式得 $ 2m{t}^{2}-2t-5m=0 $ ,即 $ m=\dfrac{2t}{2{t}^{2}-5}=\dfrac{2}{2t-\dfrac{5}{t}} $ .
当 $ t\geqslant 2 $ 时,函数 $ y=2t $ 和 $ y=-\dfrac{5}{t} $ 均单调递增,
$ \therefore y=2t-\dfrac{5}{t} $ 在 $ [2,+\mathrm{\infty }) $ 上单调递增,
$ \therefore 2t-\dfrac{5}{t}\geqslant \dfrac{3}{2} $ , $ \therefore \dfrac{2}{2t-\dfrac{5}{t}}\in (0,\dfrac{4}{3}] $ ,
$ \therefore $ 实数 $ m $ 的取值范围为 $ (0,\dfrac{4}{3}] $ .
解析:






