4.4.3 不同函数增长的差异
一、刷基础
1.当 $ x $ 越来越大时,下列函数增长速度变化最快的是( )
A. $ y=100x $
B. $ y={\left(\dfrac{\mathrm{e}}{2}\right) ^ {x}} $
C. $ y={ \log }_{2}x $
D. $ y={x}^{100} $
答案:B
解析:因为指数函数 $ y={\left(\dfrac{\mathrm{e}}{2}\right) ^ {x}} $ 是几何级数增长,所以当 $ x $ 越来越大时,增长速度变化最快.故选 $ \mathrm{B} $ .
2.(多选)函数 $ f(x)={2}^{x} $ , $ g(x)={ \log }_{\frac{1}{2}}x $ , $ ℎ(x)={x}^{-1} $ 在区间 $ (0,+\mathrm{\infty }) $ 上( )(多选)
A. $ f(x) $ 的递增速度越来越快
B. $ g(x) $ 的递减速度越来越慢
C. $ ℎ(x) $ 的递减速度越来越慢
D. $ g(x) $ 的递减速度慢于 $ ℎ(x) $ 的递减速度
答案:ABC
解析:作出三个函数在区间 $ (0,+\mathrm{\infty }) $ 上的图象,如图所示,

根据指数函数、对数函数及幂函数的图象和性质可知在区间 $ (0,+\mathrm{\infty }) $ 上,
$ f(x) $ 的递增速度越来越快,故 $ \mathrm{A} $ 正确;
$ g(x) $ 的递减速度越来越慢,故 $ \mathrm{B} $ 正确;
$ ℎ(x) $ 的递减速度越来越慢,故 $ \mathrm{C} $ 正确;
$ g(x) $ 的递减速度快于 $ ℎ(x) $ 的递减速度,故 $ \mathrm{D} $ 错误.故选 $ \mathrm{A}\mathrm{B}\mathrm{C} $ .
3.以下四种说法中,正确的是( )
A.幂函数增长的速度比一次函数增长的速度快
B.已知 $ a > 1 $ ,则对任意的 $ x > 0 $ , $ {a}^{x} > { \log }_{a}x $
C.对任意的 $ x > 0 $ , $ {x}^{a} > { \log }_{a}x $
D.不一定存在 $ {x}_{0} $ ,当 $ x > {x}_{0} $ 时,总有 $ {a}^{x} > {x}^{a} > { \log }_{a}x $
答案:D
解析:对于选项 $ \mathrm{A} $ ,幂函数与一次函数的增长速度分别受幂指数及一次项系数的影响,幂指数与一次项系数不确定,增长速度不能比较大小,故 $ \mathrm{A} $ 错误;
对于选项 $ \mathrm{B} $ ,取 $ a=1.1 $ , $ x=2 $ ,此时 $ {a}^{x}={1.1}^{2} < 2 < { \log }_{1.1}2={ \log }_{a}x $ ,故 $ \mathrm{B} $ 错误;
对于选项 $ \mathrm{C} $ ,当 $ 0 < a < 1 $ 时,结合幂函数与对数函数的图象易知 $ {x}^{a} > { \log }_{a}x $ 不恒成立,故 $ \mathrm{C} $ 错误;
对于选项 $ \mathrm{D} $ ,当 $ a > 1 $ 时,结合指数函数、幂函数和对数函数的图象易知,一定存在 $ {x}_{0} $ ,使得当 $ x > {x}_{0} $ 时,总有 $ {a}^{x} > {x}^{a} > { \log }_{a}x $ ,但若去掉限制条件“ $ a > 1 $ ”,则结论不成立,故 $ \mathrm{D} $ 正确.故选 $ \mathrm{D} $ .
4.从甲地到乙地的距离约为 $ 240\mathrm{k}\mathrm{m} $ ,经多次实验得到一辆汽车每小时耗油量 $ Q( $ 单位: $ \mathrm{L}) $ 与速度 $ v( $ 单位: $ \mathrm{k}\mathrm{m}/\mathrm{h} ) (0\leqslant v\leqslant 120 ) $ 的下列数据:
$ v $ | 0 | 40 | 60 | 80 | 120 |
$ Q $ | 0.000 | 6.667 | 8.125 | 10.000 | 20.000 |
为了描述汽车每小时耗油量与速度的关系,下列四个模型中你认为最符合实际的函数模型是( )
A. $ Q=\dfrac{1}{v+1}+b $
B. $ Q=a{v}^{3}+b{v}^{2}+cv $
C. $ Q={0.5}^{v}+a $
D. $ Q=k{ \log }_{a}v+b $
答案:B
解析:由图表中数据可知函数模型满足①定义域为 $ [0,120] $ ;②在定义域内单调递增;③函数图象过原点.
函数 $ \mathbf{Q}=\dfrac{1}{v+1}+b $ 和 $ \mathbf{Q}={0.5}^{v}+a $ 在定义域内单调递减,不满足条件②,故 $ \mathrm{A}\mathrm{C} $ 错误;
函数 $ \mathbf{Q}=k{ \log }_{a}v+b $ 中,0不在函数的定义域内,不满足条件①,故 $ \mathrm{D} $ 错误;
$ \mathrm{B} $ 选项:当 $ a > 0 $ , $ b > 0 $ , $ c > 0 $ 时, $ Q=a{v}^{3}+b{v}^{2}+cv $ 满足条件①②③,故 $ \mathrm{B} $ 正确.故选 $ \mathrm{B} $ .
5.某工程需要向一个容器内源源不断地注入某种液体,有三种方案可以选择,这三种方案的注入量随时间变化如图所示:
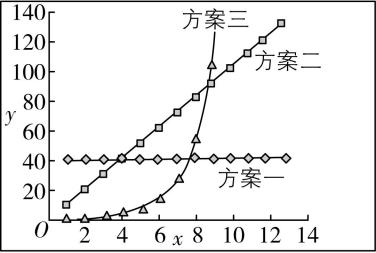
横轴为时间(单位:小时),纵轴为注入量,根据以上信息,若使注入量最多,下列说法中错误的是( )
A.注入时间在3小时以内(含3小时),采用方案一
B.注入时间恰为4小时,不采用方案三
C.注入时间恰为6小时,采用方案二
D.注入时间恰为10小时,采用方案二
答案:D
解析:对 $ \mathrm{A} $ ,由题图可知,注入时间在3小时以内(含3小时)时,方案一的注入量大于其他两种方案,故 $ \mathrm{A} $ 正确;
对 $ \mathrm{B} $ ,当注入时间恰为4小时时,由题图可知,方案三的注入量小于其他两个方案,故 $ \mathrm{B} $ 正确;
对 $ \mathrm{C} $ ,当注入时间恰为6小时时,方案二的注入量大于其他两个方案,故 $ \mathrm{C} $ 正确;
对 $ \mathrm{D} $ ,当注入时间恰为10小时时,由题图可知方案三的注入量最大,故应选择方案三, $ \mathrm{D} $ 错误.故选 $ \mathrm{D} $ .
6.已知 $ a={2.1}^{1.3} $ , $ b={0.3}^{1.3} $ , $ c={ \log }_{2}0.8 $ , $ d={2.1}^{1.9} $ ,则 $ a $ , $ b $ , $ c $ , $ d $ 的大小关系为( )
A. $ d > a > b > c $
B. $ a > d > c > b $
C. $ b > c > a > d $
D. $ c > a > d > b $
答案:A
解析: $ y={2.1}^{x} $ 是 $ \boldsymbol{R} $ 上的增函数,故 $ {2.1}^{1.9} > {2.1}^{1.3} > {2.1}^{0}=1 $ ,即 $ d > a > 1 $ .
由 $ y={0.3}^{x} $ 是 $ \boldsymbol{R} $ 上的减函数,得 $ 1={0.3}^{0} > {0.3}^{1.3} > 0 $ ,即 $ 0 < b < 1 $ .
由 $ y={ \log }_{2}x $ 是 $ (0,+\mathrm{\infty }) $ 上的增函数,得 $ { \log }_{2}0.8 < { \log }_{2}1=0 $ ,即 $ c < 0 $ .
综上所述, $ d > a > b > c $ .故选 $ \mathrm{A} $ .
7.(多选)在同一坐标系中,对于函数 $ f(x)={x}^{2} $ 与 $ g(x)={2}^{x} $ 的图象,下列说法错误的是( )(多选)
A. $ f(x) $ 与 $ g(x) $ 的图象有两个交点
B. $ f(x) $ 与 $ g(x) $ 的图象有三个交点
C. $ \exists {x}_{0} > 0 $ ,当 $ x > {x}_{0} $ 时, $ f(x) $ 的图象恒在 $ g(x) $ 的图象的上方
D. $ \exists {x}_{0} > 0 $ ,当 $ x > {x}_{0} $ 时, $ g(x) $ 的图象恒在 $ f(x) $ 的图象的上方
答案:AC
解析: $ f(1)=1 $ , $ g(1)=2 $ , $ f(2)=g(2)=4 $ , $ f(3)=9 $ , $ g(3)=8 $ , $ f(4)=g(4)=16 $ , $ f(5)=25 $ , $ g(5)=32 $ ,
则可在同一坐标系中作出两函数图象如图所示.
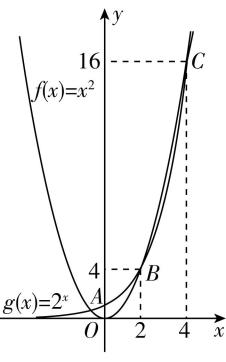
显然两函数的图象有三个交点 $ A $ , $ B $ , $ C $ ,故 $ \mathrm{A} $ 错误, $ \mathrm{B} $ 正确;
由于指数函数的增长速度大于幂函数的增长速度,
所以当 $ x > 4 $ 时, $ g(x) $ 的图象恒在 $ f(x) $ 的图象的上方,故 $ \mathrm{C} $ 错误, $ \mathrm{D} $ 正确.故选 $ \mathrm{A}\mathrm{C} $ .
8.当 $ 2 < x < 4 $ 时, $ {2}^{x} $ , $ {x}^{2} $ , $ { \log }_{2}x $ 的大小关系是( )
A. $ {2}^{x} > {x}^{2} > { \log }_{2}x $
B. $ {x}^{2} > {2}^{x} > { \log }_{2}x $
C. $ {2}^{x} > { \log }_{2}x > {x}^{2} $
D. $ {x}^{2} > { \log }_{2}x > {2}^{x} $
答案:B
解析:在同一坐标系中画出函数 $ y={ \log }_{2}x $ , $ y={x}^{2} $ , $ y={2}^{x} $ 的图象如图所示,在区间 $ (2,4) $ 内从上往下依次是 $ y={x}^{2} $ , $ y={2}^{x} $ , $ y={ \log }_{2}x $ 的图象, $ \therefore {x}^{2} > {2}^{x} > { \log }_{2}x $ .故选 $ \mathrm{B} $ .




