第4.3,4.4节综合训练

因为函数 $ f (x )={ \log }_{a}x (a > 0 $ ,且 $ a\ne 1) $ 与函数 $ g(x)={a}^{x} $ 互为反函数，所以函数 $ g(x)={a}^{x} $ 的图象经过点 $ (3,2) $ .故选 $ \mathrm{C} $ .

因为函数 $ f (x )=\begin{cases} (a+2)^{x},x < 1,\\ {x}^{2}-2ax+2,x\geqslant 1\end{cases} (a > -2 $ 且 $ a\ne -1) $ 在定义域内单调，而 $ y={x}^{2}-2ax+2 $ 在 $ [1,+\mathrm{\infty }) $ 上只能单调递增，

所以 $ f (x )=\begin{cases} (a+2)^{x},x < 1,\\ {x}^{2}-2ax+2,x\geqslant 1\end{cases} $ 在定义域内单调递增，

所以 $ \begin{cases}a+2 > 1,\\ a\leqslant 1,\\ {1}^{2}-2a+2\geqslant a+2,\end{cases} $ 解得 $ -1 < a\leqslant \dfrac{1}{3} $ ，

即 $ a $ 的取值范围为 $ (-1,\dfrac{1}{3}] $ .故选 $ \mathrm{B} $ .

由题意得 $ f(x)={ \log }_{a}(x+1)+{ \log }_{a}(1-x)={ \log }_{a}(1-{x}^{2}) $ , $ x\in [0,\dfrac{\sqrt{2}}{2}] $ ,

令 $ t=1-{x}^{2} $ ,则 $ t\in [\dfrac{1}{2},1] $ ,

则函数 $ f(x)={ \log }_{a}(1-{x}^{2}) $ , $ x\in [0,\dfrac{\sqrt{2}}{2}] $ ,即 $ g(t)={ \log }_{a}t $ , $ t\in [\dfrac{1}{2},1] $ .

当 $ a > 1 $ 时, $ g(t)={ \log }_{a}t $ 在 $ [\dfrac{1}{2},1] $ 上单调递增,由 $ f(x)_{ \max }-f(x)_{ \min }=1 $ 可得 $ { \log }_{a}1-{ \log }_{a}\frac{1}{2}=1 $ ,解得 $ a=2 $ ；

当 $ 0 < a < 1 $ 时, $ g(t)={ \log }_{a}t $ 在 $ [\dfrac{1}{2},1] $ 上单调递减,由 $ f(x)_{ \max }-f(x)_{ \min }=1 $ 可得 $ { \log }_{a}\frac{1}{2}-{ \log }_{a}1=1 $ ,解得 $ a=\dfrac{1}{2} $ .

故 $ a $ 的值为2或 $ \dfrac{1}{2} $ ,故选 $ \mathrm{C} $ .

因为幂函数 $ f(x)=({m}^{2}-2m-2){x}^{m} $ 在 $ (0,+\mathrm{\infty }) $ 上单调递减，

所以 $ \begin{cases}{m}^{2}-2m-2=1,\\ m < 0,\end{cases} $ 解得 $ m=-1 $ ，

则 $ g (x )={ \log }_{a} (x-1 )+2 (a > 0 $ 且 $ a\ne 1) $ ，

因为 $ y={ \log }_{a}x(a > 0 $ 且 $ a\ne 1) $ 的图象过定点 $ (1,0) $ ，所以 $ g(x) $ 的图象过定点 $ (2,2) $ .故选 $ \mathrm{C} $ .

因为 $ f(x) $ 为 $ \boldsymbol{R} $ 上的奇函数，所以 $ g(x)=xf(x) $ 是偶函数，

又因为 $ g(x) $ 在区间 $ (-\mathrm{\infty },0) $ 上单调递减，所以 $ g(x) $ 在区间 $ (0,+\mathrm{\infty }) $ 上单调递增.

又 $ { \log }_{\frac{1}{2}}\frac{1}{3}={ \log }_{23} < 2 $ ， $ {2}^{\mathrm{\pi }} > {2}^{\sqrt{3}} > 2 $ ，

所以 $ {2}^{\mathrm{\pi }} > {2}^{\sqrt{3}} > { \log }_{\frac{1}{2}}\frac{1}{3} > 0 $ ，所以 $ c < b < a $ .故选 $ \mathrm{B} $ .

由题意 $ L(1,x)=-L(x,1)= \ln x $ ,所以 $ L(x,1)=- \ln x $ ,

当 $ u > 1 $ 时, $ L(u,v)=L(1,v)-L(1,u)= \ln v- \ln u $ ；

当 $ v < 1 $ 时, $ L(u,v)=L(u,1)-L(v,1)= \ln v- \ln u $ ；

当 $ u < 1 < v $ 时, $ L(u,v)=L(u,1)+L(1,v)= \ln v- \ln u $ ；

当 $ v=1 $ 或 $ u=1 $ 时, $ L(u,v)= \ln v- \ln u $ 也成立.

综上所述, $ L(u,v)= \ln v- \ln u $ .

对于选项 $ \mathrm{A} $ ： $ L(\dfrac{1}{6},\dfrac{1}{3})= \ln \dfrac{1}{3}- \ln \dfrac{1}{6}= \ln 2 $ , $ L(4,8)= \ln 8- \ln 4= \ln 2 $ ,

所以 $ L(\dfrac{1}{6},\dfrac{1}{3})=L(4,8) $ ,故 $ \mathrm{A} $ 正确；

对于选项 $ \mathrm{B} $ ： $ L({4}^{50},{3}^{100})= \ln {3}^{100}- \ln {4}^{50}= \ln {3}^{100}- \ln {2}^{100}=100( \ln 3- \ln 2) $ ,

且 $ L(2,3)= \ln 3- \ln 2 $ ,所以 $ L({4}^{50},{3}^{100})=100L(2,3) $ ,故 $ \mathrm{B} $ 正确；

对于选项 $ \mathrm{C} $ ：如图,

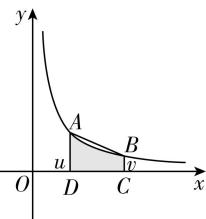
因为 $ {S}_{阴影} < {S}_{梯形ABCD} $ ,所以 $ L(u,v)= \ln v- \ln u < $ $ \dfrac{1}{2}(v-u)(\dfrac{1}{v}+\dfrac{1}{u})=\dfrac{1}{2}\cdot \dfrac{{v}^{2}-{u}^{2}}{uv}=\dfrac{1}{2}(\dfrac{v}{u}-\dfrac{u}{v}) $ ,

即 $ 2L(u,v) < \dfrac{v}{u}-\dfrac{u}{v} $ ,故 $ \mathrm{C} $ 正确;

对于选项 $ \mathrm{D} $ ：取 $ u=1 $ , $ v=2 $ ,则 $ L({u}^{u},{v}^{u})=L(1,2)= \ln 2 < 2-1=1 $ ,故 $ \mathrm{D} $ 错误.故选 $ \mathrm{A}\mathrm{B}\mathrm{C} $ .

因为 $ { \log }_{3}x-{ \log }_{3}y < {\left(\dfrac{1}{3}\right) ^ {x}}-{\left(\dfrac{1}{3}\right) ^ {y}} $ 成立,所以 $ x > 0 $ , $ y > 0 $ 且 $ { \log }_{3}x-{\left(\dfrac{1}{3}\right) ^ {x}} < { \log }_{3}y-{\left(\dfrac{1}{3}\right) ^ {y}} $ .

令函数 $ f(x)={ \log }_{3}x-{\left(\dfrac{1}{3}\right) ^ {x}} $ ,因为 $ y={ \log }_{3}x $ , $ y=-{\left(\dfrac{1}{3}\right) ^ {x}} $ 都在 $ (0,+\mathrm{\infty }) $ 上单调递增,所以函数 $ f(x)={ \log }_{3}x-{\left(\dfrac{1}{3}\right) ^ {x}} $ 在 $ (0,+\mathrm{\infty }) $ 上单调递增,由 $ { \log }_{3}x-{\left(\dfrac{1}{3}\right) ^ {x}} < { \log }_{3}y-{\left(\dfrac{1}{3}\right) ^ {y}} $ 得 $ f(x) < f(y) $ ,所以 $ 0 < x < y $ .

因为函数 $ y=\dfrac{1}{x} $ 在 $ (0,+\mathrm{\infty }) $ 上单调递减,所以 $ \dfrac{1}{x} > \dfrac{1}{y} $ , $ \mathrm{A} $ 正确；

因为函数 $ y={x}^{3} $ 在 $ (0,+\mathrm{\infty }) $ 上单调递增,所以 $ {x}^{3} < {y}^{3} $ , $ \mathrm{B} $ 正确；

因为 $ x-y < 0 $ ,函数 $ y={2}^{x} $ 在 $ (-\mathrm{\infty },+\mathrm{\infty }) $ 上单调递增,所以 $ {2}^{x-y} < {2}^{0}=1 $ , $ \mathrm{C} $ 正确；

$ y-x > 0 $ , $ \ln (y-x) $ 的符号可正可负, $ \mathrm{D} $ 错误.故选 $ \mathrm{A}\mathrm{B}\mathrm{C} $ .