2.下列图象表示的函数中有两个零点的有( )
A.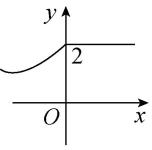
B.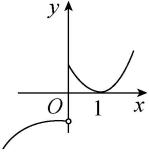
C.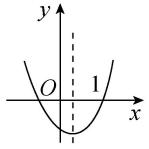
D.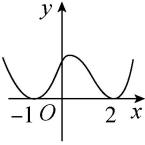
函数有两个零点就是函数图象与 $ x $ 轴有两个交点,故选 $ \mathrm{C}\mathrm{D} $ .
1.函数 $ f(x)={\mathrm{e}}^{x}-2 $ 的零点为( )
A.1
B. $ (1,0) $
C. $ \ln 2 $
D. $ ( \ln 2,0) $
由 $ f(x)=0⇒{\mathrm{e}}^{x}-2=0⇒{\mathrm{e}}^{x}=2⇒x= \ln 2 $ .故选 $ \mathrm{C} $ .
2.下列图象表示的函数中有两个零点的有( )
A.
B.
C.
D.
函数有两个零点就是函数图象与 $ x $ 轴有两个交点,故选 $ \mathrm{C}\mathrm{D} $ .
3.若函数 $ f(x)=ax+b(a\ne 0) $ 有一个零点是1,则函数 $ g(x)=a{x}^{3}+bx $ 的零点是( )
A.0,2
B. $ -1 {\rm ,3} $
C. $ -1 {\rm ,0,4} $
D. $ -1 {\rm ,0,1} $
由题意可得 $ f(1)=a+b=0 $ ,可得 $ b=-a $ ,可得 $ g(x)=a{x}^{3}+bx=a{x}^{3}-ax $ ,令 $ g(x)=0 $ ,因此 $ a{x}^{3}-ax=ax(x-1)(x+1)=0 $ ,解得 $ x=0 $ 或 $ x=1 $ 或 $ x=-1 $ ,因此函数 $ g(x)=a{x}^{3}+bx $ 的零点是 $ -1 {\rm ,0,1} $ .故选 $ \mathrm{D} $ .
4.函数 $ f(x)=\begin{cases} \ln x-{x}^{2}+2x,x > 0,\\ {x}^{2}-2x-3,x\leqslant 0\end{cases} $ 的零点个数为( )
A.1
B.2
C.3
D.4
当 $ x > 0 $ 时,令 $ f(x)=0 $ ,则 $ \ln x={x}^{2}-2x $ ,
则函数 $ f(x) $ 在 $ (0,+\mathrm{\infty }) $ 上的零点个数为函数 $ y= \ln x $ 与函数 $ y={x}^{2}-2x $ , $ x\in (0,+\mathrm{\infty }) $ 图象的交点个数,
在同一直角坐标系中作出两个函数的大致图象,如图所示,
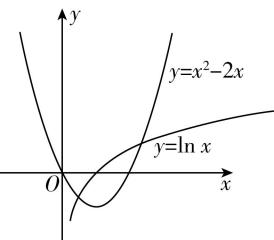
由图可知,当 $ x > 0 $ 时,函数 $ f(x) $ 的零点有2个;
当 $ x\leqslant 0 $ 时,令 $ f(x)={x}^{2}-2x-3=0 $ ,解得 $ x=-1 $ 或 $ x=3 $ (舍去),
则当 $ x\leqslant 0 $ 时,函数 $ f(x) $ 的零点有1个.
综上,函数 $ f(x) $ 的零点有3个.故选 $ \mathrm{C} $ .
5.函数 $ f(x)=x-\sqrt{x}-6 $ 的零点是 .
9
由题意可知 $ f(x) $ 的定义域为 $ {x|x\geqslant 0} $ ,令 $ f(x)=x-\sqrt{x}-6=0 $ ,可得 $ {\left(\sqrt{x}\right) ^ {2}}-\sqrt{x}-6=0 $ ,解得 $ \sqrt{x}=-2 $ (舍去)或 $ \sqrt{x}=3 $ , $ \therefore x=9 $ .
6.已知 $ f(x)={ \log }_{3}(x+1)-{ \log }_{3}(x-1) $ .
(1)求 $ g(x)=f(x)-2 $ 的零点;
(2)关于 $ x $ 的方程 $ f(x)={ \log }_{3}\frac{a}{x} $ 有解,求实数 $ a $ 的取值范围.
见解析
(1)由题设, $ g(x)=f(x)-2={ \log }_{3}\frac{x+1}{9(x-1)} $ 且定义域为 $ {x|x > 1} $ ,
所以令 $ g(x)=0 $ ,即 $ \dfrac{x+1}{9(x-1)}=1 $ ,解得 $ x=\dfrac{5}{4} > 1 $ ,则 $ g(x) $ 的零点为 $ \dfrac{5}{4} $ .
(2)由(1)及题设知 $ \dfrac{x+1}{x-1}=\dfrac{a}{x} $ 在 $ {x|x > 1} $ 上有解,且 $ a > 0 $ ,所以 $ a=\dfrac{x(x+1)}{x-1}=x-1+\dfrac{2}{x-1}+3\geqslant 3+2\sqrt{(x-1)\cdot \dfrac{2}{x-1}}=3+2\sqrt{2} $ ,当且仅当 $ x=\sqrt{2}+1 $ 时等号成立,所以实数 $ a $ 的取值范围为 $ [3+2\sqrt{2},+\mathrm{\infty }) $ .
7.已知函数 $ f(x) $ 的图象是一条连续不断的曲线,且 $ f(0) > 0 $ , $ f(1) > 0 $ , $ f(2) > 0 $ , $ f(3) < 0 $ , $ f(4) < 0 $ ,则在下列区间中,一定包含 $ f(x) $ 零点的区间是( )
A. $ (0,1) $
B. $ (1,2) $
C. $ (2,3) $
D. $ (3,4) $
因为 $ f(x) $ 的图象是一条连续不断的曲线,且 $ f(0)f(1) > 0 $ , $ f(1)f(2) > 0 $ , $ f(2)f(3) < 0 $ , $ f(3)f(4) > 0 $ ,所以由函数零点存在定理可知一定包含 $ f(x) $ 零点的区间是 $ (2,3) $ .故选 $ \mathrm{C} $ .
8.函数 $ f(x)={x}^{3}-\dfrac{1}{x}-2 $ 在区间 $ (0,+\mathrm{\infty }) $ 内的零点个数是( )
A.0
B.1
C.2
D.3
由 $ f(x)={x}^{3}-\dfrac{1}{x}-2 $ 在 $ (0,+\mathrm{\infty }) $ 上单调递增,且 $ f(1)=-2 < 0 < f(2)=\dfrac{11}{2} $ ,所以函数在区间 $ (0,+\mathrm{\infty }) $ 内的零点个数是1.故选 $ \mathrm{B} $ .
9.若函数 $ f(x)=2{x}^{2}-3ax+2 $ 有两个零点,且分别在 $ (-2,-1) $ 与 $ (-1,0) $ 内,则实数 $ a $ 的取值范围是( )
A. $ (-\dfrac{5}{3},\dfrac{4}{3}) $
B. $ (-\mathrm{\infty },-\dfrac{5}{3})\cup (\dfrac{4}{3},+\mathrm{\infty }) $
C. $ (-\dfrac{5}{3},-\dfrac{4}{3}) $
D. $ (\dfrac{4}{3},\dfrac{5}{3}) $
由题意可得
$ \begin{cases}f(-2)\cdot f(-1)=(8+6a+2)(2+3a+2) < 0,\\ f(-1)\cdot f(0)=(2+3a+2)×2 < 0,\end{cases} $
解得 $ -\dfrac{5}{3} < a < -\dfrac{4}{3} $ .故选 $ \mathrm{C} $ .
10.已知三个函数 $ f(x)={2}^{x}+x-2 $ , $ g(x)={x}^{3}-8 $ , $ h(x)={ \log }_{2}x+x-2 $ 的零点依次为 $ a $ , $ b $ , $ c $ ,则 $ a+b+c= $ ( )
A.6
B.5
C.4
D.3
令 $ f(x)={2}^{x}+x-2=0 $ , $ h(x)={ \log }_{2}x+x-2=0 $ ,则 $ {2}^{x}=2-x $ , $ { \log }_{2}x=2-x $ ,即 $ a $ , $ c $ 分别为直线 $ y=2-x $ 与函数 $ y={2}^{x} $ , $ y={ \log }_{2}x $ 图象交点的横坐标.因为 $ y={2}^{x} $ , $ y={ \log }_{2}x $ 互为反函数,其图象关于直线 $ y=x $ 对称,而直线 $ y=2-x $ 与 $ y=x $ 垂直,交点坐标为 $ (1,1) $ ,所以 $ a+c=2 $ .又由 $ {b}^{3}-8=0 $ 得 $ b=2 $ ,所以 $ a+b+c=4 $ .故选 $ \mathrm{C} $ .
11.已知函数 $ f(x) $ 的定义域为 $ (-\mathrm{\infty },0)\cup (0,+\mathrm{\infty }) $ , $ f(x) $ 是奇函数,且当 $ x > 0 $ 时, $ f(x)={x}^{2}-x+a $ .若函数 $ g(x)=f(x)-x $ 恰有两个零点,则实数 $ a $ 的取值范围是( )
A. $ (-\mathrm{\infty },0) $
B. $ (-\mathrm{\infty },0] $
C. $ (-\mathrm{\infty },1] $
D. $ (-\mathrm{\infty },0]\cup {1} $
因为 $ f(x) $ 是奇函数,所以 $ g(x)=f(x)-x $ 也是奇函数,所以要使函数 $ g(x)=f(x)-x $ 恰有两个零点,则只需要当 $ x > 0 $ 时,函数 $ g(x)=f(x)-x $ 恰有一个零点即可.
由 $ x > 0 $ , $ g(x)=f(x)-x=0 $ ,得 $ g(x)={x}^{2}-2x+a=0 $ .
若 $ \mathrm{\Delta }=0 $ ,即 $ 4-4a=0 $ ,解得 $ a=1 $ ,零点为1;
若 $ \mathrm{\Delta } > 0 $ ,要使当 $ x > 0 $ 时,函数 $ g(x) $ 只有一个零点,则 $ a\leqslant 0 $ ,所以此时 $ \begin{cases}\mathrm{\Delta }=4-4a > 0,\\ a\leqslant 0,\end{cases} $ 解得 $ a\leqslant 0 $ .
综上可得, $ a\leqslant 0 $ 或 $ a=1 $ .故选 $ \mathrm{D} $ .
12.(多选)设函数 $ f(x)=\begin{cases}\dfrac{1}{x}-1,0 < x\leqslant 1,\\ 1-\dfrac{1}{x},x > 1.\end{cases} $ 若 $ {x}_{1} < {x}_{2} $ ,且 $ f({x}_{1})=f({x}_{2}) $ ,则( )(多选)
A. $ 0 < {x}_{1} < \dfrac{1}{2} $
B. $ 2{x}_{1}{x}_{2}={x}_{1}+{x}_{2} $
C. $ {x}_{1}{x}_{2} > 1 $
D. $ {x}_{1}+{x}_{2} > 2 $
作出函数 $ f(x) $ 的大致图象,如图所示,

由图可知, $ 0 < {x}_{1} < 1 < {x}_{2} $ ,由 $ f({x}_{1})=f({x}_{2}) $ 知, $ \dfrac{1}{{x}_{1}}-1=1-\dfrac{1}{{x}_{2}} $ ,即 $ \dfrac{1}{{x}_{1}}+\dfrac{1}{{x}_{2}}=2 $ ,
则 $ 2{x}_{1}{x}_{2}={x}_{1}+{x}_{2} $ ,则 $ {x}_{1}=\dfrac{{x}_{2}}{2{x}_{2}-1}=\dfrac{1}{2-\dfrac{1}{{x}_{2}}} > \dfrac{1}{2} $ ,故 $ \mathrm{A} $ 错误, $ \mathrm{B} $ 正确;
由 $ 2{x}_{1}{x}_{2}={x}_{1}+{x}_{2} $ ,得 $ {x}_{1}{x}_{2}=\dfrac{{x}_{1}+{x}_{2}}{2} > \sqrt{{x}_{1}{x}_{2}} $ ,所以 $ {x}_{1}{x}_{2} > 1 $ ,故 $ \mathrm{C} $ 正确;所以 $ {x}_{1}+{x}_{2}=2{x}_{1}{x}_{2} > 2 $ ,故 $ \mathrm{D} $ 正确.故选 $ \mathrm{B}\mathrm{C}\mathrm{D} $ .
13.(多选)已知函数 $ f(x)=(x-a)(x-b)-1(a < b) $ 恰有两个零点 $ c $ , $ d(c < d) $ ,则下列结论正确的是( )(多选)
A. $ f(c)=f(d)=0 $
B.方程 $ f(x)=-1 $ 的解集为 $ {a $ , $ b} $
C.不等式 $ f(x) < 0 $ 的解集为 $ {x|a < x < b} $
D. $ a $ , $ b $ , $ c $ , $ d $ 的大小关系是 $ d > b > a > c $
对于 $ \mathrm{A} $ ,因为 $ c $ , $ d(c < d) $ 是函数 $ f(x)=(x-a)(x-b)-1(a < b) $ 的两个零点,所以 $ f(c)=f(d)=0 $ ,故 $ \mathrm{A} $ 正确;
对于 $ \mathrm{B} $ ,方程 $ f(x)=-1⇒(x-a)(x-b)-1=-1⇒(x-a)(x-b)=0⇒x=a $ 或 $ b $ ,所以方程 $ f(x)=-1 $ 的解集为 $ {a $ , $ b} $ ,故 $ \mathrm{B} $ 正确;
对于 $ \mathrm{C} $ ,因为函数 $ f(x)=(x-a)(x-b)-1(a < b) $ 恰有两个零点 $ c $ , $ d(c < d) $ ,所以 $ f(x)=(x-a)(x-b)-1=(x-c)(x-d) < 0⇒c < x < d $ ,所以不等式 $ f(x) < 0 $ 的解集为 $ {x|c < x < d} $ ,故 $ \mathrm{C} $ 错误;
对于 $ \mathrm{D} $ ,先画出 $ y=(x-a)(x-b) $ 的图象,再将 $ y=(x-a)(x-b) $ 的图象向下平移一个单位长度得到 $ f(x)=(x-a)(x-b)-1 $ 的图象,如图所示,
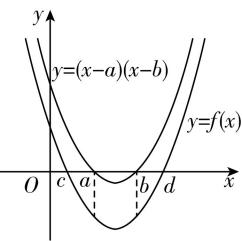
由图可知 $ d > b > a > c $ ,故 $ \mathrm{D} $ 正确.故选 $ \mathrm{A}\mathrm{B}\mathrm{D} $ .
14.已知函数 $ f(x)=2{x}^{2}-3x-5 $ ,则 $ f(x) $ 的零点为( )
A.1和 $ -\dfrac{5}{2} $
B. $ -1 $ 和 $ \dfrac{5}{2} $
C. $ (-1,0) $ 和 $ (\dfrac{5}{2},0) $
D. $ (-\dfrac{5}{2},0) $ 和 $ (1,0) $
对于函数 $ f(x)=2{x}^{2}-3x-5 $ ,令 $ f(x)=0 $ ,即 $ 2{x}^{2}-3x-5=0 $ ,解得 $ x=-1 $ 或 $ x=\dfrac{5}{2} $ ,所以 $ f(x) $ 的零点为 $ -1 $ 和 $ \dfrac{5}{2} $ .故选 $ \mathrm{B} $ .
15.“函数 $ f(x) $ 满足 $ f(a)f(b) < 0 $ ”是“函数 $ f(x) $ 在区间 $ (a,b) $ 上有零点”的( )
A.充分不必要条件
B.必要不充分条件
C.充要条件
D.既不充分也不必要条件
若函数 $ f(x) $ 满足 $ f(a)f(b) < 0 $ ,根据函数零点存在定理,如果函数 $ y=f(x) $ 在区间 $ [a,b] $ 上的图象是一条连续不断的曲线,并且有 $ f(a)f(b) < 0 $ ,那么函数 $ y=f(x) $ 在区间 $ (a,b) $ 上有零点.但是这里并没有说明函数 $ f(x) $ 在区间 $ [a,b] $ 上的图象是连续不断的,
比如函数 $ f(x)=\begin{cases}\dfrac{1}{x},x\ne 0,\\ 1,x=0,\end{cases} $ 当 $ a=-1 $ , $ b=1 $ 时, $ f(-1)f(1)=-1×1=-1 < 0 $ ,
但 $ f(x) $ 在 $ (-1,1) $ 上没有零点,所以“函数 $ f(x) $ 满足 $ f(a)f(b) < 0 $ ”不能推出“函数 $ f(x) $ 在区间 $ (a,b) $ 上有零点”,充分性不成立.
若函数 $ f(x) $ 在区间 $ (a,b) $ 上有零点,比如函数 $ f(x)={x}^{2} $ 在区间 $ (-1,1) $ 上有零点0,此时 $ f(-1)f(1)=1×1=1 > 0 $ ,这说明“函数 $ f(x) $ 在区间 $ (a,b) $ 上有零点”不能推出“函数 $ f(x) $ 满足 $ f(a)f(b) < 0 $ ”,必要性不成立.所以“函数 $ f(x) $ 满足 $ f(a)f(b) < 0 $ ”是“函数 $ f(x) $ 在区间 $ (a,b) $ 上有零点”的既不充分也不必要条件.故选 $ \mathrm{D} $ .
16.已知函数f(x)=ax $ {\rm ^{2}} $ -x+a,“函数f(x)在(0,2)上有两个不相等的零点”是“ $ \dfrac{1}{4} $ <a< $ \dfrac{1}{2} $ ”的 ( )
A.充分不必要条件
B.必要不充分条件
C.充分必要条件
D.既不充分也不必要条件
①当a=0时,f(x)=-x在(0,2)上无零点;
②当a>0时,则 $ \begin{cases}\Delta =1-4{a}^{2} > 0,\\ f(0)=a > 0,\\ f(2)=5a-2 > 0,\\ 0 < \dfrac{1}{2a} < 2,\end{cases} $ 解得 $ \dfrac{2}{5} $ <a< $ \dfrac{1}{2} $ ;
③当a<0时,则 $ \begin{cases}\Delta =1-4{a}^{2} > 0,\\ f(0)=a < 0,\\ f(2)=5a-2 < 0,\\ 0 < \dfrac{1}{2a} < 2,\end{cases} $ 无解.
综上所述,f(x)在(0,2)上有两个不相等的零点时, $ \dfrac{2}{5} $ <a< $ \dfrac{1}{2} {\rm \mathit{.}} $ ∵ $ (\dfrac{2}{5},\dfrac{1}{2}) $ ⫋ $ (\dfrac{1}{4},\dfrac{1}{2}) $ ,∴“函数f(x)在(0,2)上有两个不相等的零点”是“ $ \dfrac{1}{4} $ <a< $ \dfrac{1}{2} $ ”的充分不必要条件.故选A.
17.(多选)已知函数 $ f(x)={x}^{2}-ax+1 $ , $ g(x)=- \ln x $ .若 $ \max {m $ , $ n} $ 表示 $ m $ , $ n $ 中的最大者,设函数 $ ℎ(x)= \max {f(x) $ , $ g(x)}(x > 0) $ ,则下列结论正确的是( )(多选)
A.若 $ ℎ(x) $ 没有零点,则 $ a $ 的取值范围为 $ (-\mathrm{\infty },2) $
B.若 $ ℎ(x) $ 只有1个零点,则 $ a $ 的取值集合为 $ {2} $
C.若 $ ℎ(x) $ 有2个零点,则 $ a $ 的取值范围为 $ (2,+\mathrm{\infty }) $
D. $ \forall a\in \mathbf{R} $ , $ ℎ(x)\geqslant 0 $
$ f(x) $ 图象的对称轴方程为 $ x=\dfrac{a}{2} $ ,开口向上,
当 $ \dfrac{a}{2}\leqslant 0 $ ,即 $ a\leqslant 0 $ 时,对任意 $ x\in (0,+\mathrm{\infty }) $ ,都有 $ f(x) > f(0)=1 $ ,所以 $ ℎ(x)\geqslant f(x) > 0 $ , $ ℎ(x) $ 没有零点.
当 $ \dfrac{a}{2} > 0 $ ,即 $ a > 0 $ 时,令 $ {x}^{2}-ax+1=0 $ , $ \mathrm{\Delta }={a}^{2}-4 < 0 $ ,解得 $ -2 < a < 2 $ ,所以 $ 0 < a < 2 $ .
当 $ 0 < a < 2 $ 时, $ f(x) > 0 $ ,所以 $ ℎ(x)\geqslant f(x) > 0 $ , $ ℎ(x) $ 没有零点.
当 $ a=2 $ 时, $ f(x)={x}^{2}-2x+1 $ .
当 $ x\ne 1 $ 时, $ f(x) > 0 $ ,所以 $ ℎ(x)\geqslant f(x) > 0 $ ;当 $ x=1 $ 时, $ ℎ(1)= \max {f(1) $ , $ g(1)}=0 $ ,所以 $ ℎ(x) $ 有1个零点.
当 $ a > 2 $ 时, $ 2-a < 0 $ .
当 $ x\in (0,1) $ 时, $ ℎ(x)\geqslant g(x) > 0 $ ;当 $ x=1 $ 时, $ ℎ(1)= \max {f(1) $ , $ g(1)}= \max {2-a $ , $ 0}=0 $ ;
当 $ x\in (1,+\mathrm{\infty }) $ 时, $ g(x) < 0 $ , $ f(1)=2-a < 0 $ , $ f(a)=1 $ ,所以 $ f(x) $ 在 $ (1,+\mathrm{\infty }) $ 上有1个零点,则 $ ℎ(x) $ 在 $ (1,+\mathrm{\infty }) $ 上有1个零点.所以 $ ℎ(x) $ 有2个零点.
设 $ f(x) $ 在 $ (1,+\mathrm{\infty }) $ 上的零点为 $ {x}_{1} $ ,则当 $ x\in (1,{x}_{1}) $ 时, $ f(x) < 0 $ ,所以当 $ x\in (1,{x}_{1}) $ 时, $ ℎ(x) < 0 $ , $ \mathrm{D} $ 错误.
综上,当 $ a < 2 $ 时, $ ℎ(x) $ 没有零点;当 $ a=2 $ 时, $ ℎ(x) $ 有1个零点;当 $ a > 2 $ 时, $ ℎ(x) $ 有2个零点, $ \mathrm{A}\mathrm{B}\mathrm{C} $ 正确,故选 $ \mathrm{A}\mathrm{B}\mathrm{C} $ .
18.已知函数 $ f(x)=\begin{cases}{\mathrm{e}}^{x}+a,x\leqslant 0,\\ \mid \ln x\mid ,x > 0,\end{cases}g(x)=f(x)+x $ .若 $ g(x) $ 有且仅有一个零点,则实数 $ a $ 的取值范围是( )
A. $ (-\mathrm{\infty },-1) $
B. $ [-1,+\mathrm{\infty }) $
C. $ (-\mathrm{\infty },0) $
D. $ [0,+\mathrm{\infty }) $
画出 $ f(x) $ 的大致图象如图所示 $ {\rm .} g(x) $ 有且仅有一个零点等价于方程 $ f(x)=-x $ 有且仅有一个解,结合 $ y=f(x) $ 的图象与 $ y=-x $ 的图象可知,当 $ {\mathrm{e}}^{0}+a\geqslant 0 $ ,即 $ a\geqslant -1 $ 时, $ y=f(x) $ 的图象与 $ y=-x $ 的图象有唯一的交点.故选 $ \mathrm{B} $ .
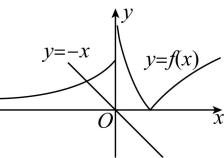
19.已知函数 $ f(x)=\begin{cases}x+2,x\leqslant 0,\\ x+\dfrac{1}{x},x > 0,\end{cases} $ 若函数 $ g(x)={[f(x)]}^{2}+4f(x)+a(a\in \boldsymbol{R}) $ 有三个不同的零点,则实数 $ a $ 的取值范围为( )
A. $ (-\mathrm{\infty },4) $
B. $ (-\mathrm{\infty },4] $
C. $ (-\mathrm{\infty },-12) $
D. $ (-\mathrm{\infty },-12] $
当 $ x\leqslant 0 $ 时,函数 $ f(x)=x+2 $ 在 $ (-\mathrm{\infty },0] $ 上单调递增, $ f(x)\leqslant f(0)=2 $ ,
当 $ x > 0 $ 时,函数 $ f(x)=x+\dfrac{1}{x}\geqslant 2\sqrt{x\cdot \dfrac{1}{x}}=2 $ ,当且仅当 $ x=1 $ 时取等号.画出函数 $ y=f(x) $ 的大致图象,如图所示.
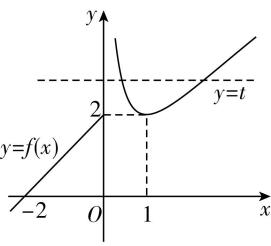
令 $ f(x)=t $ ,观察图象知,当 $ t < 2 $ 时,方程 $ f(x)=t $ 有一个根,当 $ t\geqslant 2 $ 时,方程 $ f(x)=t $ 有两个不等实根.
函数 $ g(x)={[f(x)]}^{2}+4f(x)+a(a\in \boldsymbol{R}) $ 有三个零点,等价于函数 $ ℎ(t)={t}^{2}+4t+a $ 有两个零点 $ {t}_{1} $ , $ {t}_{2} $ ,并满足 $ {t}_{1} < 2 $ , $ {t}_{2}\geqslant 2 $ .
函数 $ ℎ(t) $ 的图象的对称轴为直线 $ t=-2 $ ,于是得 $ ℎ(2)=a+12\leqslant 0 $ ,解得 $ a\leqslant -12 $ .
所以实数 $ a $ 的取值范围为 $ (-\mathrm{\infty },-12] $ .故选 $ \mathrm{D} $ .
20.在数学中,对于满足一定条件的连续函数 $ g(x) $ ,存在实数 $ {x}_{0} $ ,使得 $ g({x}_{0})={x}_{0} $ ,我们就称该函数为“不动点”函数,实数 $ {x}_{0} $ 为该函数的“不动点”.已知函数 $ g(x)=a{x}^{2}+(a-2)x+1 $ 在区间 $ (-\mathrm{\infty },\dfrac{1}{2}) $ 上恰有两个不同的“不动点”,则实数 $ a $ 的取值范围为( )
A. $ (\dfrac{3}{2},+\mathrm{\infty }) $
B. $ (9,+\mathrm{\infty }) $
C. $ (-\mathrm{\infty },0)\cup (9,+\mathrm{\infty }) $
D. $ (-\mathrm{\infty },\dfrac{2}{3}) $
根据题意可得 $ g(x)=a{x}^{2}+(a-2)x+1=x $ 在 $ (-\mathrm{\infty },\dfrac{1}{2}) $ 上恰有两个不同的解,即 $ f(x)=a{x}^{2}+(a-3)x+1 $ 在区间 $ (-\mathrm{\infty },\dfrac{1}{2}) $ 上恰有两个零点,
所以 $ \begin{cases}a > 0,\\ -\dfrac{a-3}{2a} < \dfrac{1}{2},\\ f\left(\dfrac{1}{2}\right)=a\cdot {\left(\dfrac{1}{2}\right)}^{2}+\left(a-3\right)×\dfrac{1}{2}+1 > 0,\\ \mathrm{\Delta }={\left(a-3\right)}^{2}-4a > 0\end{cases} $
或 $ \begin{cases}a < 0,\\ -\dfrac{a-3}{2a} < \dfrac{1}{2},\\ f\left(\dfrac{1}{2}\right)=a\cdot {\left(\dfrac{1}{2}\right)}^{2}+\left(a-3\right)×\dfrac{1}{2}+1 < 0,\\ \mathrm{\Delta }={\left(a-3\right)}^{2}-4a > 0,\end{cases} $
解得 $ a > 9 $ 或 $ a < 0 $ .故选 $ \mathrm{C} $ .
1.函数 $ f(x)={ \log }_{2}x-{\left(\dfrac{1}{\mathrm{e}}\right) ^ {x}} $ 的零点所在区间为( )
A. $ (0,1) $
B. $ (1,2) $
C. $ (2,3) $
D. $ (3,4) $
易知 $ f(x)={ \log }_{2}x-{\left(\dfrac{1}{\mathrm{e}}\right) ^ {x}} $ 单调递增, $ f(1)={ \log }_{2}1-\dfrac{1}{\mathrm{e}} < 0 $ , $ f(2)={ \log }_{2}2-{\left(\dfrac{1}{\mathrm{e}}\right) ^ {2}} > 0 $ ,所以 $ f(x) $ 的零点所在区间为 $ (1,2) $ ,故选 $ \mathrm{B} $ .
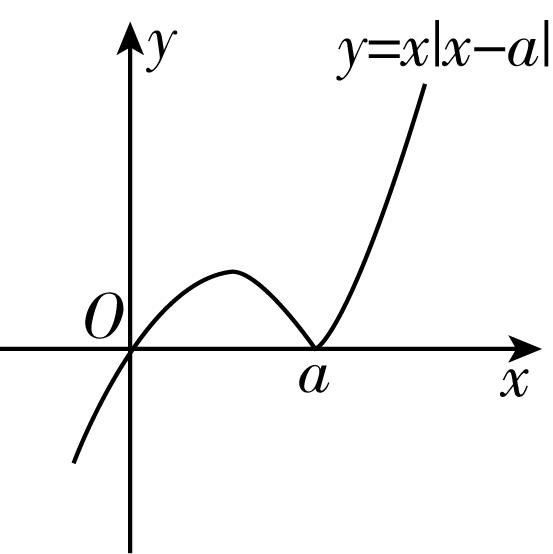
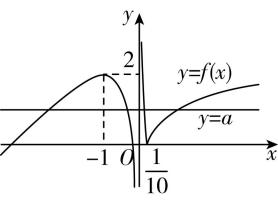
2.借助信息技术画出函数 $ y=x|x-a| $ ( $ a $ 为实数)的图象,当 $ a=1.5 $ 时图象如图所示,则函数 $ y=x|x-1.5|- \ln \text{ }x $ 的零点个数为( )
A.3
B.2
C.1
D.0
令 $ y=x\left|x-1.5\right|- \ln \text{ }x=0 $ ,则 $ x\left|x-1.5\right|= \ln \text{ }x $ ,所以函数 $ y=x|x-1.5|- \ln \text{ }x $ 的零点个数即为 $ y=x\left|x-1.5\right| $ 与 $ y= \ln \text{ }x $ 的图象交点个数,在题图的基础上作出函数 $ y= \ln \text{ }x $ 的图象,如图所示.
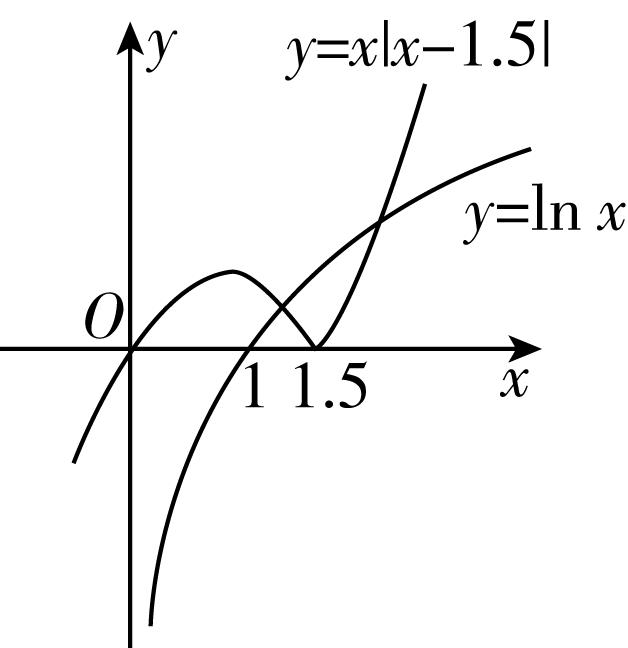
结合图象可知 $ y=x\left|x-1.5\right| $ 与 $ y= \ln \text{ }x $ 的图象有2个交点,所以函数 $ y=x\left|x-1.5\right|- \ln \text{ }x $ 有2个零点.故选 $ \mathrm{B} $ .
3.设 $ a $ 是函数 $ f(x)={2}^{x}-{ \log }_{\frac{1}{2}}x $ 的零点.若 $ {x}_{0} > a $ ,则 $ f({x}_{0}) $ 的值满足( )
A. $ f({x}_{0})=0 $
B. $ f({x}_{0}) < 0 $
C. $ f({x}_{0}) > 0 $
D. $ f({x}_{0}) $ 的符号不确定
$ \because $ 函数 $ y={2}^{x} $ 和 $ y={ \log }_{2}x $ 在 $ (0,+\mathrm{\infty }) $ 上均单调递增, $ \therefore f(x)={2}^{x}-{ \log }_{\frac{1}{2}}x={2}^{x}+{ \log }_{2}x $ 在 $ (0,+\mathrm{\infty }) $ 上单调递增.又 $ \because a $ 是函数 $ f(x)={2}^{x}+{ \log }_{2}x $ 的零点, $ \therefore f(a)=0 $ , $ \therefore $ 当 $ {x}_{0} > a $ 时, $ \text{ }f({x}_{0}) > f(a)=0 $ .故选 $ \mathrm{C} $ .
4.已知函数 $ f(x)=\begin{cases}{x}^{2}-4x,x\leqslant 2,\\ 4-\mid 2x-12\mid ,x > 2,\end{cases} $ 若关于 $ x $ 的方程 $ f(x)-f(2-a)=0 $ 至少有两个不等的实根,则实数 $ a $ 的取值范围为( )
A. $ [-8,2\sqrt{2}] $
B. $ (-\mathrm{\infty },-8]\cup [2\sqrt{2},+\mathrm{\infty }) $
C. $ (-8,2\sqrt{2}) $
D. $ [-2\sqrt{2},8] $
因为 $ f(x)=\begin{cases}{x}^{2}-4x,x\leqslant 2,\\ 4-\mid 2x-12\mid ,x > 2,\end{cases} $
所以 $ f(x)=\begin{cases}{x}^{2}-4x,x\leqslant 2,\\ 2x-8,2 < x\leqslant 6,\\ 16-2x,x > 6,\end{cases} $
作出函数 $ f(x) $ 的图象,如图所示,
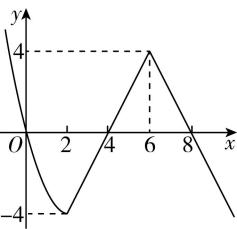
关于 $ x $ 的方程 $ f(x)-f(2-a)=0 $ 至少有两个不等的实根,即函数 $ f(x) $ 的图象与直线 $ y=f(2-a) $ 至少有两个不同的交点,所以 $ -4\leqslant f(2-a)\leqslant 4 $ ,
当 $ x\leqslant 2 $ 时,令 $ f(x)={x}^{2}-4x=4 $ ,解得 $ x=2-2\sqrt{2} $ ,
当 $ x > 6 $ 时,令 $ f(x)=16-2x=-4 $ ,解得 $ x=10 $ ,
所以 $ 2-2\sqrt{2}\leqslant 2-a\leqslant 10 $ ,解得 $ -8\leqslant a\leqslant 2\sqrt{2} $ .故选 $ \mathrm{A} $ .
5.设函数 $ f(x)=2023{\mathrm{e}}^{x}+2024 \ln x $ ,满足 $ f(a)f(b)f(c) < 0(0 < a < b < c) $ ,若 $ f(x) $ 存在零点 $ {x}_{0} $ ,则下列选项中一定错误的是( )
A. $ {x}_{0}\in (a,b) $
B. $ {x}_{0}\in (b,c) $
C. $ {x}_{0}\in (a,c) $
D. $ {x}_{0}\in (c,+\mathrm{\infty }) $
因为 $ y={\mathrm{e}}^{x} $ , $ y= \ln x $ 在 $ (0,+\mathrm{\infty }) $ 上单调递增,
所以 $ f(x)=2023{\mathrm{e}}^{x}+2024 \ln x $ 在 $ (0,+\mathrm{\infty }) $ 上为增函数,
又 $ 0 < a < b < c $ ,所以 $ f(a) < f(b) < f(c) $ ,
又 $ f(a)f(b)f(c) < 0 $ ,
所以 $ f(a) < 0 $ , $ f(b) > 0 $ , $ f(c) > 0 $ 或 $ f(a) < 0 $ , $ f(b) < 0 $ , $ f(c) < 0 $ .
当 $ f(a) < 0 $ , $ f(b) > 0 $ , $ f(c) > 0 $ 时,
由 $ f(x) $ 存在零点 $ {x}_{0} $ ,可知 $ {x}_{0}\in (a,b) $ ,且 $ (a,b)⫋(a,c) $ ,此时 $ \mathrm{A} $ , $ \mathrm{C} $ 选项正确, $ \mathrm{B} $ , $ \mathrm{D} $ 选项错误;
当 $ f(a) < 0 $ , $ f(b) < 0 $ , $ f(c) < 0 $ 时,
由 $ f(x) $ 存在零点 $ {x}_{0} $ ,可知 $ {x}_{0}\in (c,+\mathrm{\infty }) $ ,
此时 $ \mathrm{A} $ , $ \mathrm{B} $ , $ \mathrm{C} $ 选项错误, $ \mathrm{D} $ 选项正确.
综上,选项中一定错误的是 $ \mathrm{B} $ 选项,故选 $ \mathrm{B} $ .
6.已知函数 $ f(x)=\begin{cases}5-{2}^{\mid x-2\mid },x\geqslant 0,\\ \dfrac{2x+3}{x+1},x < 0,\end{cases} $ 若函数 $ g(x)=[f(x)]^{2}-(m+2)\cdot |f(x)|+2m $ 有7个不同的零点,则实数 $ m $ 的取值范围为( )
A. $ (1,2]\cup [3,4) $
B. $ (1,2]\cup (3,4) $
C. $ (2,3)\cup (4,+\mathrm{\infty }) $
D. $ (4,+\mathrm{\infty }) $
令 $ |f(x)|=t $ ,由函数 $ g(x)={[f(x)]}^{2}-(m+2)|f(x)|+2m $ 有7个不同的零点可知方程 $ {t}^{2}-(m+2)t+2m=(t-2)(t-m)=0 $ 有两个不相等的实数根 $ {t}_{1} $ , $ {t}_{2} $ ,且 $ {t}_{1} $ , $ {t}_{2} $ 对应的 $ x $ 的取值共有7个.
作出 $ y=|f(x)| $ 的图象如图所示:
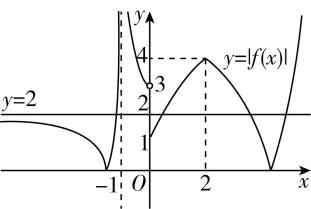
不妨设 $ {t}_{1}=|f(x)|=2 $ ,即 $ y=|f(x)| $ 与 $ y={t}_{1} $ 的图象有4个交点,对应的 $ x $ 的取值共有4个,
因此 $ |f(x)|={t}_{2} $ 对应的 $ x $ 的取值共有3个,即 $ y=|f(x)| $ 与 $ y={t}_{2} $ 的图象有3个交点,
由图可知,当 $ m > 4 $ 时满足题意.故选 $ \mathrm{D} $ .
7.已知函数 $ f(x) $ , $ g(x) $ 分别是定义在 $ \boldsymbol{R} $ 上的偶函数和奇函数,且满足 $ f(x)+g(x)={2}^{x}-x $ .若关于 $ x $ 的方程 $ {2}^{|x|}-2\lambda f(x)+{\lambda }^{2}=0 $ 有唯一的实数解,则实数 $ \lambda $ 的值为( )
A. $ \dfrac{1}{2} $
B. $ -\dfrac{1}{2} $
C.1
D. $ -1 $
$ \because f(x) $ , $ g(x) $ 分别是定义在 $ \boldsymbol{R} $ 上的偶函数和奇函数,
$ \therefore f(-x)=f(x) $ , $ g(-x)=-g(x) $ .
又 $ \because f(x)+g(x)={2}^{x}-x $ ,①
$ \therefore f(-x)+g(-x)=f(x)-g(x)={2}^{-x}+x $ .②
$ \mathrm{①}+\mathrm{②} $ 得 $ 2f(x)={2}^{x}+{2}^{-x} $ ,
$ \therefore f(x)=\dfrac{1}{2}({2}^{x}+{2}^{-x}) $ .
令 $ ℎ(x)={2}^{|x|}-2\lambda f(x)+{\lambda }^{2}={2}^{|x|}-\lambda ({2}^{x}+{2}^{-x})+{\lambda }^{2} $ .
$ \because ℎ(x)=ℎ(-x) $ , $ \therefore ℎ(x) $ 为偶函数,
$ \therefore $ 当且仅当 $ x=0 $ 时, $ ℎ(x)=0 $ ,
$ \therefore 1-2\lambda +{\lambda }^{2}=0 $ ,解得 $ \lambda =1 $ .故选 $ \mathrm{C} $ .
8.(多选)已知函数 $ f(x)={x}^{3}+a{x}^{2}+bx+c $ 有三个零点 $ -1 {\rm ,1} $ , $ {x}_{0} $ ,且函数 $ g(x)=a{x}^{2}+bx+c $ ,则下列判断正确的是( )(多选)
A. $ {x}_{0}=-a $
B.函数 $ y=g(x) $ 可能不存在零点
C.函数 $ y=g(x) $ 可能有一个零点
D.函数 $ y=g(x) $ 可能有两个零点
因为 $ -1 $ 和1是 $ f(x) $ 的零点,所以 $ \begin{cases}1+a+b+c=0,\\ -1+a-b+c=0,\end{cases} $ 解得 $ b=-1 $ , $ c=-a $ ,
所以 $ f(x)={x}^{3}+a{x}^{2}-x-a=x({x}^{2}-1)+a({x}^{2}-1)=(x+a)({x}^{2}-1) $ ,因为 $ {x}_{0} $ 为函数 $ f(x) $ 的零点,且 $ {x}_{0}\ne ±1 $ ,所以 $ {x}_{0}=-a $ ,故 $ \mathrm{A} $ 正确;当 $ a=0 $ 时, $ g(x)=-x $ 有一个零点,故 $ \mathrm{C} $ 正确;当 $ a\ne 0 $ 时,对于 $ g(x)=a{x}^{2}-x-a $ , $ \mathrm{\Delta }=1+4{a}^{2} > 0 $ ,所以 $ y=g(x) $ 有两个零点,故 $ \mathrm{D} $ 正确;综上, $ y=g(x) $ 可能有一个零点或两个零点,故 $ \mathrm{B} $ 错误.故选 $ \mathrm{A}\mathrm{C}\mathrm{D} $ .
9.已知 $ f(x) $ 是定义在 $ (-\mathrm{\infty },0)\cup (0,+\mathrm{\infty }) $ 上的偶函数,当 $ x > 0 $ 时, $ f(x)=\begin{cases}{ \log }_{2}\mid x\mid ,0 < x < 1,\\ \mid 4-{x}^{2}\mid ,x\geqslant 1,\end{cases} $ 则下列说法正确的是( )(多选)
A.函数 $ f(x) $ 在 $ (0,+\mathrm{\infty }) $ 上单调递增
B.函数 $ f(x) $ 有两个零点
C.不等式 $ f(x)\leqslant 3 $ 的解集为 $ [-\sqrt{7},\sqrt{7}] $
D.方程 $ f(f(x))-5=0 $ 有6个不相等的实数根
由题意,函数 $ f(x) $ 的图象如图所示.
对于 $ \mathrm{A} $ , $ f(x) $ 在 $ (1,2) $ 上单调递减, $ \mathrm{A} $ 错误.
对于 $ \mathrm{B} $ ,令 $ f(x)=0 $ ,即 $ \left|4-{x}^{2}\right|=0 $ ,解得 $ x=±2 $ , $ f(x) $ 只有2个零点, $ \mathrm{B} $ 正确.
对于 $ \mathrm{C} $ ,由图知只需 $ f(x)\leqslant 3 $ 得 $ \left|4-{x}^{2}\right|\leqslant 3 $ ,解得 $ [-\sqrt{7},0)\cup (0,\sqrt{7}] $ , $ \mathrm{C} $ 错误.
对于 $ \mathrm{D} $ , $ f(f(x))=5 $ ,即 $ \left|4-{[f(x)]}^{2}\right|=5 $ ,且 $ \left|f(x)\right|\geqslant 1 $ ,解得 $ f(x)=±3 $ .若 $ f(x)=3 $ ,即 $ \left|4-{x}^{2}\right|=3 $ ,解得 $ x=±1 $ 或 $ x=±\sqrt{7} $ ;若 $ f(x)=-3 $ ,即 $ { \log }_{2}\left|x\right|=-3 $ ,解得 $ x=±\dfrac{1}{8} $ , $ \mathrm{D} $ 正确.故选 $ \mathrm{B}\mathrm{D} $ .
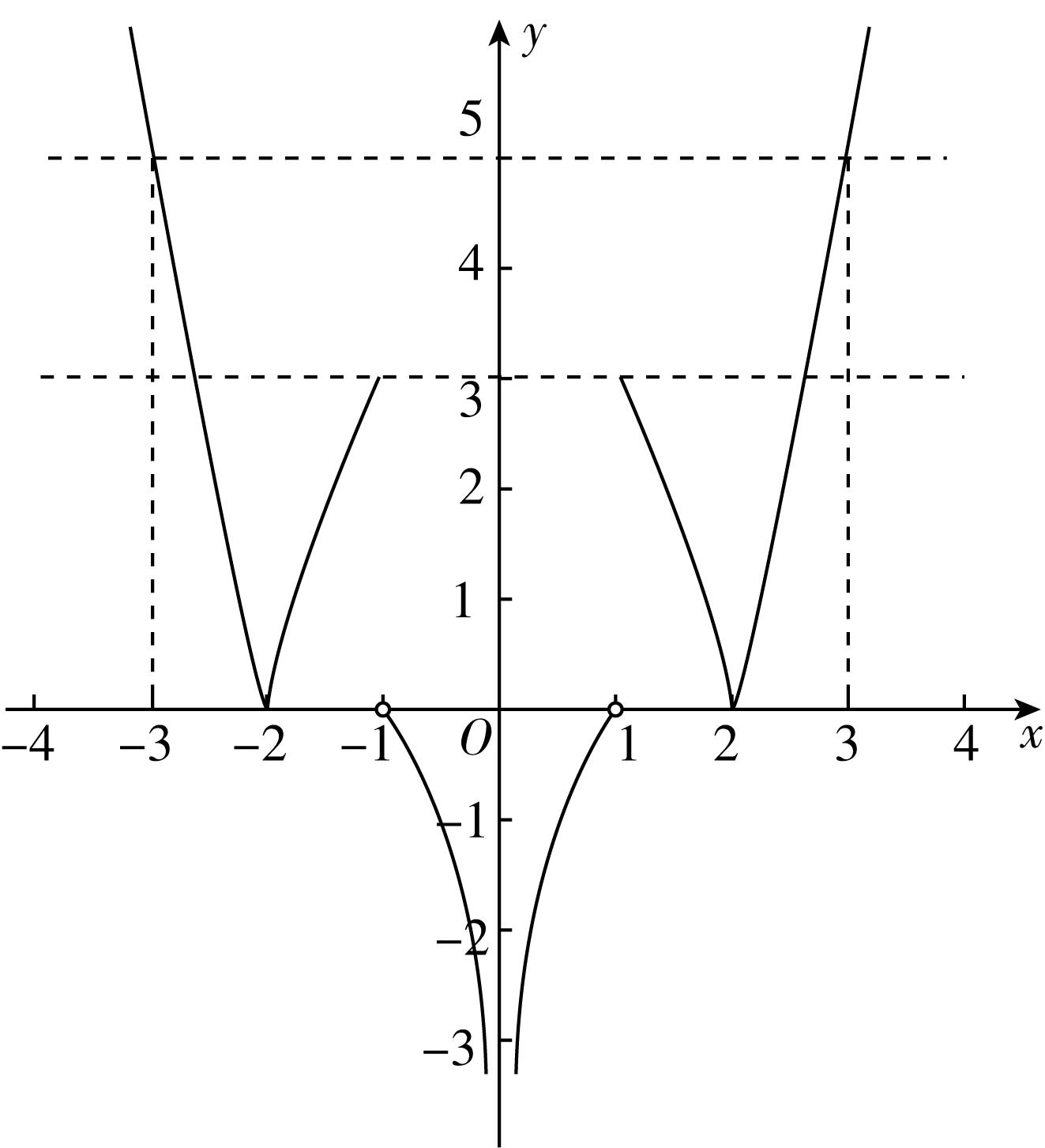
10.(多选)已知函数 $ f(x)=\begin{cases}x+\dfrac{1}{x}+4,x < 0,\\ \mid \lg x+1\mid ,x > 0,\end{cases} $ 方程 $ f(x)=a $ 有4个不同的实数根 $ {x}_{1} $ , $ {x}_{2} $ , $ {x}_{3} $ , $ {x}_{4}({x}_{1} < {x}_{2} < {x}_{3} < {x}_{4}) $ ,则( )(多选)
A. $ a > 2 $
B. $ {x}_{4}-{x}_{1} > \dfrac{11}{10} $
C. $ {x}_{3}{x}_{4}=\dfrac{1}{100} $
D. $ 2 < \dfrac{1}{{x}_{1}^{2}}+\dfrac{1}{{x}_{2}^{2}} < 14 $
当 $ x < 0 $ 时, $ -x > 0 $ ,则 $ (-x)+(-\dfrac{1}{x})\geqslant 2 $ ,则 $ x+\dfrac{1}{x}\leqslant -2 $ ,即 $ x+\dfrac{1}{x}+4\leqslant 2 $ ,当且仅当 $ x=-1 $ 时取等号,
当 $ x > 0 $ 时, $ | \lg x+1|\geqslant 0 $ ,当且仅当 $ x=\dfrac{1}{10} $ 时取等号,作出函数 $ f(x) $ 的图象如图所示,由图可知当且仅当 $ 0 < a < 2 $ 时方程 $ f(x)=a $ 有4个不同实根,故 $ \mathrm{A} $ 错误;
结合图象可得 $ {x}_{1} < -1 $ , $ {x}_{4} > \dfrac{1}{10} $ , $ {x}_{4}-{x}_{1} > \dfrac{11}{10} $ ,故 $ \mathrm{B} $ 正确;
由题得 $ \lg {x}_{3}+1\ne \lg {x}_{4}+1 $ 且 $ | \lg {x}_{3}+1|=| \lg {x}_{4}+1| $ ,所以 $ \lg {x}_{3}+1+ \lg {x}_{4}+1=0 $ ,所以 $ \lg ({x}_{3}{x}_{4})=-2 $ ,所以 $ {x}_{3}{x}_{4}=\dfrac{1}{100} $ ,故 $ \mathrm{C} $ 正确;
$ {x}_{1} $ , $ {x}_{2} $ 是方程 $ x+\dfrac{1}{x}+4=a $ ,即方程 $ {x}^{2}+(4-a)x+1=0 $ 的两个根,所以 $ {x}_{1}{x}_{2}=1 $ , $ {x}_{1}+{x}_{2}=a-4 $ ,所以 $ \dfrac{1}{{x}_{1}^{2}}+\dfrac{1}{{x}_{2}^{2}}=\dfrac{{x}_{1}^{2}+{x}_{2}^{2}}{{x}_{1}^{2}{x}_{2}^{2}}={x}_{1}^{2}+{x}_{2}^{2}={\left(a-4\right) ^ {2}}-2 $ ,由 $ 0 < a < 2 $ ,所以 $ 2 < (a-4)^{2}-2 < 14 $ ,故 $ \mathrm{D} $ 正确.故选 $ \mathrm{B}\mathrm{C}\mathrm{D} $ .
11.已知函数 $ f(x)={x}^{2}-2(a+1)x+4 $ 在区间 $ [\dfrac{1}{2},3] $ 上有两个零点,则实数 $ a $ 的取值范围是 .
$ (1,\dfrac{7}{6}] $
函数 $ f(x)={x}^{2}-2(a+1)x+4 $ 在区间 $ [\dfrac{1}{2},3] $ 上有两个零点,
即 $ {x}^{2}-2(a+1)x+4=0 $ 在区间 $ [\dfrac{1}{2},3] $ 上有两个不同的解,
即 $ 2(a+1)=x+\dfrac{4}{x} $ 在区间 $ [\dfrac{1}{2},3] $ 上有两个不同的解,
转化成 $ y=2(a+1) $ 与 $ g(x)=x+\dfrac{4}{x} $ 的图
象在区间 $ [\dfrac{1}{2},3] $ 上有两个不同的交点,
结合对勾函数的性质可知 $ g(x)=x+\dfrac{4}{x} $ 在 $ [\dfrac{1}{2},2] $ 上单调递减,在 $ [2,3] $ 上单调递增,
且 $ g(\dfrac{1}{2})=\dfrac{17}{2} $ , $ g(2)=4 $ , $ g(3)=\dfrac{13}{3} $ ,所以 $ 4 < 2(a+1)\leqslant \dfrac{13}{3} $ ,解得 $ 1 < a\leqslant \dfrac{7}{6} $ .
12.已知函数 $ f(x)= \ln x+x-3 $ , $ g(x)={\mathrm{e}}^{x}+x-3 $ (其中 $ \mathrm{e} $ 为自然对数的底数).设 $ m $ , $ n $ 分别为 $ f(x) $ , $ g(x) $ 的零点,则 $ {\mathrm{e}}^{n}+ \ln m= $ .
3
因为 $ m $ , $ n $ 分别为 $ f(x) $ , $ g(x) $ 的零点,所以 $ f(m)= \ln m+m-3=0 $ , $ g(n)={\mathrm{e}}^{n}+n-3=0 $ ,
因为 $ {\mathrm{e}}^{n}+n-3=0 $ ,所以 $ f({\mathrm{e}}^{n})={\mathrm{l}\mathrm{n}\mathrm{e}}^{n}+{\mathrm{e}}^{n}-3={\mathrm{e}}^{n}+n-3=0 $ ,且 $ {\mathrm{e}}^{n}+n=3 $ ,
因为函数 $ f(x)= \ln x+x-3 $ 为增函数,且 $ f(m)=f({\mathrm{e}}^{n})=0 $ ,所以 $ m={\mathrm{e}}^{n} $ ,所以 $ {\mathrm{e}}^{n}+ \ln m={\mathrm{e}}^{n}+{\mathrm{l}\mathrm{n}\mathrm{e}}^{n}={\mathrm{e}}^{n}+n=3 $ .
13.设函数 $ f(x)=a{x}^{2}+(2a-4)x-a+5 $ ,其中 $ a > 0 $ .若 $ f(x) $ 在区间 $ (-1,2) $ 内存在零点,求 $ a $ 的取值范围.
【解】由已知,得 $ \mathrm{\Delta }={\left(2a-4\right) ^ {2}}-4a(5-a)=4(2a-1)(a-4) $ .
(1)当 $ \mathrm{\Delta }=0 $ ,即 $ a=\dfrac{1}{2} $ 或 $ a=4 $ 时,
由 $ a=\dfrac{1}{2} $ ,得 $ f(x)=\dfrac{1}{2}{x}^{2}-3x+\dfrac{9}{2} $ ,此时 $ f(x) $ 的零点为3,不符合题意.
由 $ a=4 $ ,得 $ f(x)=4{x}^{2}+4x+1 $ ,此时 $ f(x) $ 的零点为 $ -\dfrac{1}{2} $ ,符合题意.
(2)当 $ \mathrm{\Delta } > 0 $ ,即 $ 0 < a < \dfrac{1}{2} $ 或 $ a > 4 $ 时,
①若 $ a > 4 $ ,此时 $ f(x) $ 图象的对称轴为直线 $ x=\dfrac{2-a}{a}=\dfrac{2}{a}-1\in (-1 $ , $ -\dfrac{1}{2}) $ ,
且 $ f(2)=7a-3 > 0 $ ,所以 $ f(x) $ 在区间 $ (-1,2) $ 内存在零点,符合题意.
②若 $ 0 < a < \dfrac{1}{2} $ ,此时 $ f(x) $ 图象的对称轴为直线 $ x=\dfrac{2-a}{a}=\dfrac{2}{a}-1\in (3,+\mathrm{\infty }) $ ,
所以 $ f(x) $ 在区间 $ (-1,2) $ 内单调递减.
又因为 $ f(-1)=9-2a > 0 $ ,
所以 $ f(x) $ 在区间 $ (-1,2) $ 内存在零点只需满足 $ f(2)=7a-3 < 0 $ ,解得 $ 0 < a < \dfrac{3}{7} $ .
综上, $ a $ 的取值范围是 $ (0,\dfrac{3}{7})\cup [4,+\mathrm{\infty }) $ .
14.已知函数 $ f(x)= \ln ({\mathrm{e}}^{2x}+1)+kx $ 是偶函数.
(1) 求实数 $ k $ 的值;
(2) 函数 $ ℎ (x )= \ln (m{\mathrm{e}}^{x}+\dfrac{{\mathrm{e}}^{-x}}{2}+2m ) (m > 0 $ 且 $ m\ne 1) $ ,函数 $ F(x)=f(x)-ℎ(x) $ 有2个零点,求实数 $ m $ 的取值范围.
(1) 【解】因为函数 $ f(x)= \ln ({\mathrm{e}}^{2x}+1)+kx $ 是偶函数,所以 $ f(-x)=f(x) $ ,
即 $ \ln ({\mathrm{e}}^{-2x}+1)-kx= \ln ({\mathrm{e}}^{2x}+1)+kx $ ,
所以 $ \ln ({\mathrm{e}}^{-2x}+1)- \ln ({\mathrm{e}}^{2x}+1)=2kx $ ,
即 $ \ln \dfrac{{\mathrm{e}}^{-2x}+1}{{\mathrm{e}}^{2x}+1}= \ln \dfrac{1}{{\mathrm{e}}^{2x}}=-2x=2kx $ ,所以 $ 2k=-2 $ ,得 $ k=-1 $ .
经检验当 $ k=-1 $ 时,函数 $ f(x)= \ln ({\mathrm{e}}^{2x}+1)-x $ 是偶函数.
(2) 【解】函数 $ F(x)=f(x)-ℎ(x) $ 有2个零点,
即关于 $ x $ 的方程 $ \ln (m{\mathrm{e}}^{x}+\dfrac{{\mathrm{e}}^{-x}}{2}+2m)= \ln ({\mathrm{e}}^{2x}+1)-x $ 有2个不相等的实数根,
化简上述方程得 $ \ln (m{\mathrm{e}}^{x}+\dfrac{{\mathrm{e}}^{-x}}{2}+2m)= \ln \dfrac{{\mathrm{e}}^{2x}+1}{{\mathrm{e}}^{x}} $ ,即 $ m{\mathrm{e}}^{x}+\dfrac{{\mathrm{e}}^{-x}}{2}+2m={\mathrm{e}}^{x}+{\mathrm{e}}^{-x} $ ,
所以 $ (m-1){\mathrm{e}}^{x}-\dfrac{1}{2{\mathrm{e}}^{x}}+2m=0 $ ,
所以 $ (m-1){\mathrm{e}}^{2x}-\dfrac{1}{2}+2m{\mathrm{e}}^{x}=0 $ .
令 $ t={\mathrm{e}}^{x}(t > 0) $ ,得关于 $ t $ 的方程 $ (m-1){t}^{2}+2mt-\dfrac{1}{2}=0(\ast ) $ .
记 $ p(t)=(m-1){t}^{2}+2mt-\dfrac{1}{2} $ , $ m > 0 $ 且 $ m\ne 1 $ ,
①当 $ m > 1 $ 时,函数 $ p(t) $ 的图象开口向上,图象恒过点 $ (0,-\dfrac{1}{2}) $ ,方程(*)只有1个正实根,不符合题意.
②当 $ 0 < m < 1 $ 时,函数 $ p(t) $ 的图象开口向下,图象恒过点 $ (0,-\dfrac{1}{2}) $ ,
因为 $ -\dfrac{2m}{2(m-1)} > 0 $ ,要满足题意,则方程(*)应有2个不相等的正实根,即 $ \mathrm{\Delta }={\left(2m\right) ^ {2}}+2(m-1) > 0 $ ,解得 $ m > \dfrac{1}{2} $ 或 $ m < -1 $ ,又 $ 0 < m < 1 $ ,所以 $ \dfrac{1}{2} < m < 1 $ .
综上, $ m $ 的取值范围是 $ (\dfrac{1}{2},1) $ .
15.已知函数 $ f(x)={2}^{x}-\dfrac{1}{{2}^{x}} $ .
(1) 根据函数单调性的定义证明 $ f(x) $ 在 $ \boldsymbol{R} $ 上单调递增;
(2) 设关于 $ x $ 的方程 $ f({9}^{x}+k)+f(1-4\cdot {3}^{x})=0 $ 有两个不同的实根,求 $ k $ 的取值范围.
(1) 【证明】任取 $ {x}_{1} $ , $ {x}_{2}\in \boldsymbol{R} $ ,且 $ {x}_{1} < {x}_{2} $ ,
则 $ f({x}_{1})-f({x}_{2})={2}^{{x}_{1}}-\dfrac{1}{{2}^{{x}_{1}}}-{2}^{{x}_{2}}+\dfrac{1}{{2}^{{x}_{2}}}=({2}^{{x}_{1}}-{2}^{{x}_{2}})+\dfrac{{2}^{{x}_{1}}-{2}^{{x}_{2}}}{{2}^{{x}_{1}+{x}_{2}}}=({2}^{{x}_{1}}-{2}^{{x}_{2}})(1+\dfrac{1}{{2}^{{x}_{1}+{x}_{2}}}) $ ,
因为 $ {x}_{1} < {x}_{2} $ ,所以 $ {2}^{{x}_{1}}-{2}^{{x}_{2}} < 0 $ .
又 $ 1+\dfrac{1}{{2}^{{x}_{1}+{x}_{2}}} > 0 $ ,
所以 $ f({x}_{1})-f({x}_{2})=({2}^{{x}_{1}}-{2}^{{x}_{2}})\cdot (1+\dfrac{1}{{2}^{{x}_{1}+{x}_{2}}}) < 0 $ ,即 $ f({x}_{1}) < f({x}_{2}) $ ,所以 $ f(x) $ 在 $ \boldsymbol{R} $ 上单调递增.
(2) 【解】因为 $ f(x)={2}^{x}-\dfrac{1}{{2}^{x}} $ , $ x\in \boldsymbol{R} $ ,所以 $ f(-x)={2}^{-x}-\dfrac{1}{{2}^{-x}}=\dfrac{1}{{2}^{x}}-{2}^{x}=-f(x) $ ,所以函数 $ f(x) $ 是奇函数,
因为 $ f({9}^{x}+k)+f(1-4\cdot {3}^{x})=0 $ ,所以 $ f({9}^{x}+k)=-f(1-4\cdot {3}^{x})=f(4\cdot {3}^{x}-1) $ ,
因为 $ f(x) $ 在 $ \boldsymbol{R} $ 上单调递增,所以 $ {9}^{x}+k=4\cdot {3}^{x}-1 $ 有两个不同的实根,即 $ k=-{9}^{x}+4\cdot {3}^{x}-1 $ 有两个不同的实根,
令 $ t={3}^{x} $ , $ t > 0 $ ,则 $ k=-{t}^{2}+4t-1 $ 有两个不同的正解,
即直线 $ y=k $ 与 $ g(t)=-{t}^{2}+4t-1(t > 0) $ 的图象有两个不同的交点,
作出 $ g(t)=-{t}^{2}+4t-1(t > 0) $ 的图象,如图所示:

由图可知 $ -1 < k < 3 $ ,所以实数 $ k $ 的取值范围为 $ (-1,3) $ .
16.已知 $ f(x)=\begin{cases}\mid { \log }_{2}(x+1)\mid ,-1 < x\leqslant 3,\\ \dfrac{1}{2}{x}^{2}-5x+\dfrac{25}{2},x > 3,\end{cases} $ 若 $ f(x)=m $ 有四个解 $ a $ , $ b $ , $ c $ , $ d $ 且 $ a < b < c < d $ ,则( )
A. $ ab=1 $
B. $ cd\in [21,25] $
C. $ c+d=22 $
D. $ \dfrac{1}{a}+\dfrac{1}{b}=-1 $
画出函数 $ y=f(x) $ 和 $ y=m $ 的图象如图所示.
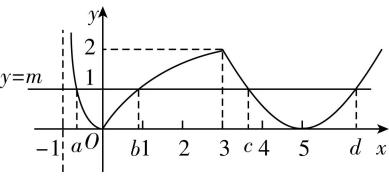
由题知, $ { \log }_{2}(a+1)=-{ \log }_{2}(b+1) $ ,
$ \therefore (a+1)(b+1)=1 $ ,
$ \therefore ab=-a-b $ ,即 $ \dfrac{1}{a}+\dfrac{1}{b}=-1 $ .
由图可得 $ c+d=10 $ , $ c\in (3,5) $ ,
$ \therefore cd=c(10-c)\in (21,25) $ .故选 $ \mathrm{D} $ .
17.(多选)已知 $ f(x)=2{x}^{2} $ , $ g(x)=3-|x| $ ,若方程 $ |f(x)-g(x)|-f(x)-g(x)+ax+4a=0 $ 有四个不同的根,则满足上述条件的 $ a $ 的可能的值为( )(多选)
A. $ \dfrac{1}{2} $
B. $ \dfrac{2}{3} $
C. $ \dfrac{4}{5} $
D.1
由题可知, $ f(x)=2{x}^{2} $ , $ g(x)=3-|x| $ ,
令 $ f(x) > g(x) $ ,即 $ 2{x}^{2} > 3-|x| $ ,解得 $ x > 1 $ 或 $ x < -1 $ ,
此时由 $ |f(x)-g(x)|-f(x)-g(x)+ax+4a=0 $ ,可得 $ f(x)-g(x)-f(x)-g(x)+ax+4a=0 $ ,则 $ g(x)=\dfrac{a}{2}x+2a $ ;
令 $ f(x)\leqslant g(x) $ ,得 $ -1\leqslant x\leqslant 1 $ ,
此时由 $ |f(x)-g(x)|-f(x)-g(x)+ax+4a=0 $ ,可得 $ g(x)-f(x)-f(x)-g(x)+ax+4a=0 $ ,则 $ f(x)=\dfrac{a}{2}x+2a $ .
令 $ F(x)=\begin{cases}g(x),x > 1\mathrm{或}x < -1,\\ f(x),-1\leqslant x\leqslant 1,\end{cases} $
则 $ |f(x)-g(x)|-f(x)-g(x)+ax+4a=0 $ 有四个不同的根,等价于 $ F(x) $ 与 $ y=\dfrac{a}{2}x+2a $ 的图象有四个交点,
又 $ y=\dfrac{a}{2}x+2a=a(\dfrac{x}{2}+2) $ 的图象过定点 $ A(-4,0) $ ,画出 $ F(x) $ 与 $ y=\dfrac{a}{2}x+2a $ 的大致图象如图所示.
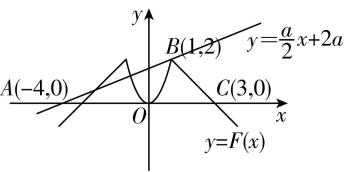
结合图象可知,当直线 $ y=\dfrac{a}{2}x+2a $ 过点 $ B(1,2) $ 或点 $ C(3,0) $ 时,与 $ F(x) $ 的图象都有三个交点,
因为 $ {k}_{AB}=\dfrac{2}{5} $ , $ {k}_{AC}=0 $ ,
所以直线 $ y=\dfrac{a}{2}x+2a $ 的斜率的取值范围为 $ (0,\dfrac{2}{5}) $ ,
即 $ 0 < \dfrac{a}{2} < \dfrac{2}{5} $ ,所以 $ 0 < a < \dfrac{4}{5} $ ,
结合选项可知,满足条件的 $ a $ 的值为 $ \dfrac{1}{2} $ , $ \dfrac{2}{3} $ .故选 $ \mathrm{A}\mathrm{B} $ .