第四章高考强化
一、刷真题
1.已知 $ ({x}_{1},{y}_{1}) $ , $ ({x}_{2},{y}_{2}) $ 是函数 $ y={2}^{x} $ 的图象上两个不同的点,则( )
A. $ { \log }_{2}\frac{{y}_{1}+{y}_{2}}{2} < \dfrac{{x}_{1}+{x}_{2}}{2} $
B. $ { \log }_{2}\frac{{y}_{1}+{y}_{2}}{2} > \dfrac{{x}_{1}+{x}_{2}}{2} $
C. $ { \log }_{2}\frac{{y}_{1}+{y}_{2}}{2} < {x}_{1}+{x}_{2} $
D. $ { \log }_{2}\frac{{y}_{1}+{y}_{2}}{2} > {x}_{1}+{x}_{2} $
答案:B
解析: $ { \log }_{2}\frac{{y}_{1}+{y}_{2}}{2}={ \log }_{2}\frac{{2}^{{x}_{1}}+{2}^{{x}_{2}}}{2}\geqslant { \log }_{2}\sqrt{{2}^{{x}_{1}}\cdot {2}^{{x}_{2}}}={ \log }_{2}{2}^{\frac{{x}_{1}+{x}_{2}}{2}}=\dfrac{{x}_{1}+{x}_{2}}{2} $ , $ \because {x}_{1}\ne {x}_{2} $ , $ \therefore $ 等号取不到,即 $ { \log }_{2}\frac{{y}_{1}+{y}_{2}}{2} > \dfrac{{x}_{1}+{x}_{2}}{2} $ .故选 $ \mathrm{B} $ .
2.已知 $ {2}^{a}=5 $ , $ { \log }_{8}3=b $ ,则 $ {4}^{a-3b}= $ ( )
A.25
B.5
C. $ \dfrac{25}{9} $
D. $ \dfrac{5}{3} $
答案:C
解析:因为 $ {2}^{a}=5 $ ,所以 $ a={ \log }_{2}5 $ , $ b={ \log }_{8}3=\dfrac{1}{3}{ \log }_{2}3 $ ,所以 $ {4}^{a-3b}={4}^{{ \log }_{2}5-{ \log }_{2}3}={2}^{2{ \log }_{2}\frac{5}{3}}={2}^{{ \log }_{2}\frac{25}{9}}=\dfrac{25}{9} $ ,故选 $ \mathrm{C} $ .
3.已知 $ a > 1 $ 且 $ \dfrac{1}{{ \log }_{8}a}-\dfrac{1}{{ \log }_{a}4}=-\dfrac{5}{2} $ ,则 $ a=\mathrm{ }\_ \mathrm{ }\_ \mathrm{ }\_ $ .
解析:因为 $ \dfrac{1}{{ \log }_{8}a}-\dfrac{1}{{ \log }_{a}4}=\dfrac{3}{{ \log }_{2}a}-\dfrac{1}{2}{ \log }_{2}a=-\dfrac{5}{2} $ ,所以 $ ({ \log }_{2}a+1)({ \log }_{2}a-6)=0 $ .又 $ a > 1 $ ,故 $ { \log }_{2}a=6 $ ,解得 $ a=64 $ .
4.若 $ f(x)= \ln |a+\dfrac{1}{1-x}|+b $ 是奇函数,则 $ a= $ , $ b= $ .
答案: $ -\dfrac{1}{2} $ ; $ \ln \text{ }2 $
解析: $ f(x)= \ln \left|\dfrac{a+1-ax}{1-x}\right|+b $ ,定义域为不等式组 $ \begin{cases}a+1-ax\ne 0,\\ 1-x\ne 0\end{cases} $ 的解集.
因为函数 $ f(x) $ 为奇函数,所以其定义域关于原点对称,
由 $ 1-x\ne 0 $ ,易知 $ x\ne 1 $ ,所以函数 $ f(x) $ 的定义域中一定不含有 $ -1 $ ,
所以 $ x=-1 $ 是方程 $ a+1-ax=0 $ 的根,即 $ a+1-a\cdot (-1)=0 $ ,解得 $ a=-\dfrac{1}{2} $ .
所以 $ f(x)= \ln \left|\dfrac{1+x}{2(1-x)}\right|+b $ ,
所以函数 $ f(x) $ 的定义域为 $ (-\mathrm{\infty },-1)\cup (-1,1)\cup (1,+\mathrm{\infty }) $ .
由函数 $ f(x) $ 为奇函数知 $ f(0)=0 $ ,所以 $ f(0)= \ln \text{ }\dfrac{1}{2}+b=0 $ ,解得 $ b= \ln \text{ }2 $ .
5.设 $ a={1.01}^{0.5} $ , $ b={1.01}^{0.6} $ , $ c={0.6}^{0.5} $ ,则 $ a $ , $ b $ , $ c $ 的大小关系为( )
A. $ a < b < c $
B. $ b < a < c $
C. $ c < b < a $
D. $ c < a < b $
答案:D
解析:依题意,函数 $ y={1.01}^{x} $ 在 $ \boldsymbol{R} $ 上单调递增,因为 $ 0 < 0.5 < 0.6 $ ,所以 $ 1 < {1.01}^{0.5} < {1.01}^{0.6} $ ,即 $ a < b $ .又 $ c={0.6}^{0.5}=\sqrt{\dfrac{6}{10}}=\dfrac{\sqrt{15}}{5} < 1 $ ,所以 $ c < a < b $ .故选 $ \mathrm{D} $ .
6.设 $ a={ \log }_{5}2 $ , $ b={ \log }_{8}3 $ , $ c=\dfrac{1}{2} $ ,则( )
A. $ c < b < a $
B. $ b < c < a $
C. $ a < c < b $
D. $ a < b < c $
答案:C
解析:因为 $ a={ \log }_{5}2 < { \log }_{5}\sqrt{5}=\dfrac{1}{2}=c $ , $ b={ \log }_{8}3 > { \log }_{9}3=\dfrac{1}{2}=c $ ,所以 $ b > c > a $ .故选 $ \mathrm{C} $ .
7.(多选)已知 $ a > 0 $ , $ b > 0 $ ,且 $ a+b=1 $ ,则( )(多选)
A. $ {a}^{2}+{b}^{2}\geqslant \dfrac{1}{2} $
B. $ {2}^{a-b} > \dfrac{1}{2} $
C. $ { \log }_{2}a+{ \log }_{2}b\geqslant -2 $
D. $ \sqrt{a}+\sqrt{b}\leqslant \sqrt{2} $
答案:ABD
解析:由 $ a > 0 $ , $ b > 0 $ , $ a+b=1 $ ,得 $ \dfrac{{a}^{2}+{b}^{2}}{2}\geqslant {\left(\dfrac{a+b}{2}\right) ^ {2}}=\dfrac{1}{4} $ ,即 $ {a}^{2}+{b}^{2}\geqslant \dfrac{1}{2} $ ,当且仅当 $ a=b=\dfrac{1}{2} $ 时取等号,故 $ \mathrm{A} $ 正确;
由 $ a > 0 $ , $ b > 0 $ , $ a+b=1 $ ,得 $ a-b=2a-1 > -1 $ ,故 $ {2}^{a-b} > \dfrac{1}{2} $ ,故 $ \mathrm{B} $ 正确;
$ { \log }_{2}a+{ \log }_{2}b={ \log }_{2}(ab)\leqslant { \log }_{2}{\left(\dfrac{a+b}{2}\right) ^ {2}}={ \log }_{2}{\left(\dfrac{1}{2}\right) ^ {2}}=-2 $ ,当且仅当 $ a=b=\dfrac{1}{2} $ 时,等号成立,故 $ \mathrm{C} $ 错误;
$ (\sqrt{a}+\sqrt{b})^{2}=a+b+2\sqrt{ab}=1+2\sqrt{ab}\leqslant 1+a+b=2 $ ,得 $ \sqrt{a}+\sqrt{b}\leqslant \sqrt{2} $ ,当且仅当 $ a=b=\dfrac{1}{2} $ 时,等号成立,故 $ \mathrm{D} $ 正确.
故选 $ \mathrm{A}\mathrm{B}\mathrm{D} $ .
8.已知 $ {9}^{m}=10 $ , $ a={10}^{m}-11 $ , $ b={8}^{m}-9 $ ,则( )
A. $ a > 0 > b $
B. $ a > b > 0 $
C. $ b > a > 0 $
D. $ b > 0 > a $
答案:A
解析:因为 $ {9}^{m}=10 $ ,所以 $ m={ \log }_{9}10 $ .
又因为 $ \lg 11× \lg 9 < {\left(\dfrac{ \lg 11+ \lg 9}{2}\right) ^ {2}}={\left(\dfrac{ \lg 99}{2}\right) ^ {2}} < 1= \lg 10× \lg 10 $ ,
所以 $ \dfrac{ \lg 10}{ \lg 9} > \dfrac{ \lg 11}{ \lg 10} $ , $ { \log }_{9}10 > { \log }_{10}11 $ .
$ a={10}^{m}-11={10}^{{ \log }_{9}10}-11 > {10}^{{ \log }_{10}11}-11=11-11=0 $ ,所以 $ a > 0 $ .
因为 $ \lg 10× \lg 8 < {\left(\dfrac{ \lg 10+ \lg 8}{2}\right) ^ {2}}={\left(\dfrac{ \lg 80}{2}\right) ^ {2}} < {\left(\dfrac{ \lg 81}{2}\right) ^ {2}}= \lg 9× \lg 9 $ ,
所以 $ \dfrac{ \lg 10}{ \lg 9} < \dfrac{ \lg 9}{ \lg 8} $ , $ { \log }_{9}10 < { \log }_{8}9 $ .
$ b={8}^{m}-9={8}^{{ \log }_{9}10}-9 < {8}^{{ \log }_{8}9}-9=9-9=0 $ ,所以 $ b < 0 $ .
综上 $ a > 0 > b $ ,故选 $ \mathrm{A} $ .
9.已知函数 $ f (x )={\mathrm{e}}^{- (x-1)^{2}} $ .记 $ a=f(\dfrac{\sqrt{2}}{2}) $ , $ b=f(\dfrac{\sqrt{3}}{2}) $ , $ c=f(\dfrac{\sqrt{6}}{2}) $ ,则( )
A. $ b > c > a $
B. $ b > a > c $
C. $ c > b > a $
D. $ c > a > b $
答案:A
解析:由题意得 $ f(x)=f(2-x) $ ,则函数 $ f(x) $ 的图象关于直线 $ x=1 $ 对称,且 $ f(x) $ 在 $ (-\mathrm{\infty },1) $ 上单调递增,在 $ (1,+\mathrm{\infty }) $ 上单调递减.
因为 $ 1 > \dfrac{\sqrt{3}}{2} > \dfrac{\sqrt{2}}{2} $ ,所以 $ b=f(\dfrac{\sqrt{3}}{2}) > f(\dfrac{\sqrt{2}}{2})=a $ , $ c=f(\dfrac{\sqrt{6}}{2})=f(2-\dfrac{\sqrt{6}}{2}) $ .因为 $ \dfrac{\sqrt{2}}{2} < 2-\dfrac{\sqrt{6}}{2} < \dfrac{\sqrt{3}}{2} $ ,所以 $ b > c > a $ ,故选 $ \mathrm{A} $ .
10.若 $ {2}^{x}-{2}^{y} < {3}^{-x}-{3}^{-y} $ ,则( )
A. $ \ln (y-x+1) > 0 $
B. $ \ln (y-x+1) < 0 $
C. $ \ln \left|x-y\right| > 0 $
D. $ \ln \left|x-y\right| < 0 $
答案:A
解析:由 $ {2}^{x}-{2}^{y} < {3}^{-x}-{3}^{-y} $ ,可得 $ {2}^{x}-{3}^{-x} < {2}^{y}-{3}^{-y} $ .
设 $ f(x)={2}^{x}-{3}^{-x} $ ,则 $ f(x) < f(y) $ .
易知 $ f(x) $ 在 $ \boldsymbol{R} $ 上为增函数,所以 $ x < y $ ,则 $ y-x+1 > 1 $ ,所以 $ \ln (y-x+1) > 0 $ ,故 $ \mathrm{A} $ 正确, $ \mathrm{B} $ 错误.
而当 $ x=1 $ , $ y=2 $ 时, $ \ln \left|x-y\right|=0 $ ,故 $ \mathrm{C} $ , $ \mathrm{D} $ 错误.故选 $ \mathrm{A} $ .
11.函数 $ y=\dfrac{2{x}^{3}}{{2}^{x}+{2}^{-x}} $ 在 $ [-6,6] $ 的图象大致为( )
A.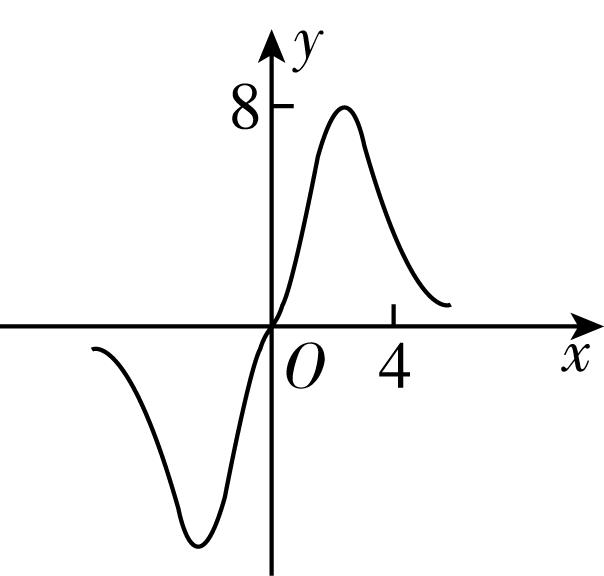
B.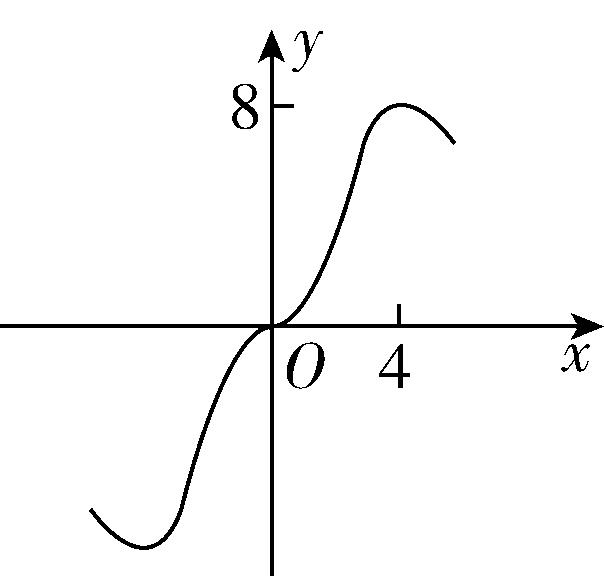
C.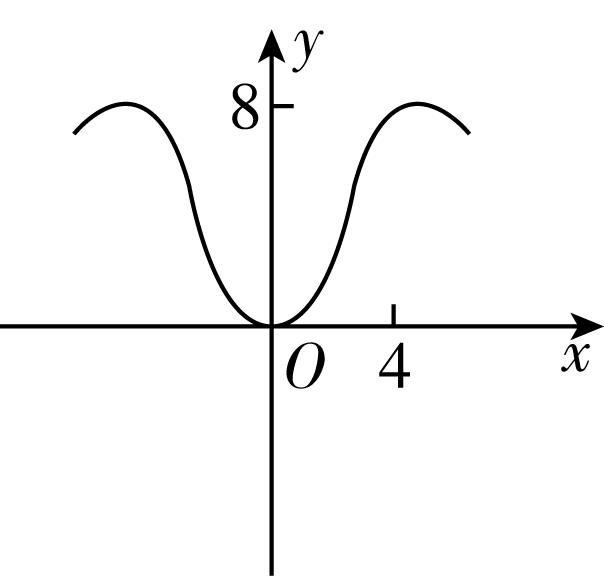
D.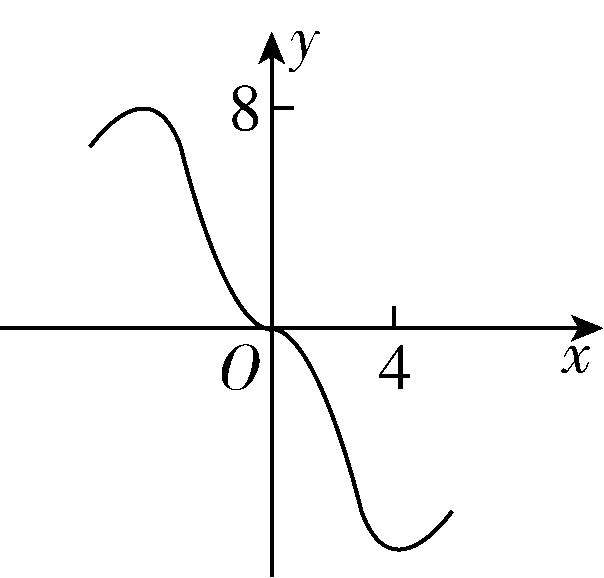
答案:B
解析:令 $ f(x)=\dfrac{2{x}^{3}}{{2}^{x}+{2}^{-x}} $ ,则 $ f(x) $ 的定义域为 $ [-6,6] $ ,且 $ f(-x)=\dfrac{-2{x}^{3}}{{2}^{-x}+{2}^{x}}=-f(x) $ , $ \therefore f(x) $ 为奇函数,排除 $ \mathrm{C} $ ;
$ f(4)=\dfrac{2×{4}^{3}}{{2}^{4}+{2}^{-4}}\approx 8 $ ,排除 $ \mathrm{A} $ , $ \mathrm{D} $ .故选 $ \mathrm{B} $ .
12.函数 $ y=\dfrac{ \ln |x|}{{x}^{2}+2} $ 的图象大致为( )
A.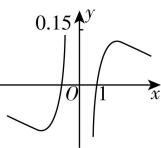
B.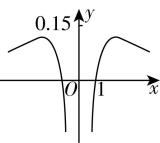
C.
D.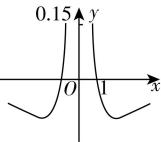
答案:B
解析:设 $ y=f(x)=\dfrac{ \ln |x|}{{x}^{2}+2} $ ,则函数 $ f(x) $ 的定义域为 $ {x|x\ne 0} $ ,关于原点对称,又 $ f(-x)=\dfrac{ \ln |-x|}{{\left(-x\right) ^ {2}}+2}=f(x) $ ,所以函数 $ f(x) $ 为偶函数,排除 $ \mathrm{A} $ , $ \mathrm{C} $ ;
当 $ x\in (0,1) $ 时, $ \ln |x| < 0 $ , $ {x}^{2}+2 > 0 $ ,所以 $ f(x) < 0 $ ,排除 $ \mathrm{D} $ .故选 $ \mathrm{B} $ .
13.已知函数 $ f(x)={2}^{x}-x-1 $ ,则不等式 $ f(x) > 0 $ 的解集是( )
A. $ (-1,1) $
B. $ (-\mathrm{\infty },-1)\cup (1,+\mathrm{\infty }) $
C. $ (0,1) $
D. $ (-\mathrm{\infty },0)\cup (1,+\mathrm{\infty }) $
答案:D
解析:因为 $ f(x)={2}^{x}-x-1 $ ,所以 $ f(x) > 0 $ 等价于 $ {2}^{x} > x+1 $ ,在同一直角坐标系中作出 $ y={2}^{x} $ 和 $ y=x+1 $ 的图象如图.

两函数图象的交点坐标分别为 $ (0,1) $ , $ (1,2) $ ,则不等式 $ {2}^{x} > x+1 $ 的解为 $ x < 0 $ 或 $ x > 1 $ ,所以不等式 $ f(x) > 0 $ 的解集为 $ (-\mathrm{\infty },0)\cup (1,+\mathrm{\infty }) $ .故选 $ \mathrm{D} $ .
14.已知函数 $ f(x)=\begin{cases}-{x}^{2}-2ax-a,x < 0,\\ {\mathrm{e}}^{x}+ \ln (x+1),x\geqslant 0\end{cases} $ 在 $ \boldsymbol{R} $ 上单调递增,则 $ a $ 的取值范围是( )
A. $ (-\mathrm{\infty },0] $
B. $ [-1,0] $
C. $ [-1,1] $
D. $ [0,+\mathrm{\infty }) $
答案:B
解析:当 $ x < 0 $ 时,函数 $ f(x)=-{x}^{2}-2ax-a=-{\left(x+a\right) ^ {2}}+{a}^{2}-a $ ,若函数 $ f(x) $ 在 $ (-\mathrm{\infty },0) $ 上单调递增,则有 $ -a\geqslant 0 $ ,即 $ a\leqslant 0 $ ;当 $ x\geqslant 0 $ 时,函数 $ f(x)={\mathrm{e}}^{x}+ \ln (x+1) $ ,函数 $ f(x) $ 在 $ [0,+\mathrm{\infty }) $ 上单调递增.因为函数 $ f(x) $ 在 $ \boldsymbol{R} $ 上单调递增,所以 $ -a\leqslant {\mathrm{e}}^{0}+ \ln (0+1)=1 $ ,解得 $ a\geqslant -1 $ .综上可得 $ -1\leqslant a\leqslant 0 $ .故选 $ \mathrm{B} $ .
15.设函数 $ f(x)={2}^{x(x-a)} $ 在区间 $ (0,1) $ 单调递减,则 $ a $ 的取值范围是( )
A. $ (-\mathrm{\infty },-2] $
B. $ [-2,0) $
C. $ (0,2] $
D. $ [2,+\mathrm{\infty }) $
答案:D
解析:因为 $ y={2}^{x} $ 在 $ \boldsymbol{R} $ 上是增函数,所以函数 $ y=x(x-a)={\left(x-\dfrac{a}{2}\right) ^ {2}}-\dfrac{{a}^{2}}{4} $ 在 $ (0,1) $ 上单调递减,所以 $ \dfrac{a}{2}\geqslant 1 $ ,解得 $ a\geqslant 2 $ ,即 $ a $ 的取值范围是 $ [2,+\mathrm{\infty }) $ ,故选 $ \mathrm{D} $ .
16.下列函数中,在区间 $ (0,+\mathrm{\infty }) $ 上单调递增的是( )
A. $ f(x)=- \ln x $
B. $ f(x)=\dfrac{1}{{2}^{x}} $
C. $ f(x)=-\dfrac{1}{x} $
D. $ f(x)={3}^{|x-1|} $
答案:C
解析:对于 $ \mathrm{A} $ ,因为 $ y= \ln x $ 在 $ (0,+\mathrm{\infty }) $ 上单调递增,所以 $ f(x)=- \ln x $ 在 $ (0,+\mathrm{\infty }) $ 上单调递减,故 $ \mathrm{A} $ 错误;对于 $ \mathrm{B} $ , $ f(x)=\dfrac{1}{{2}^{x}} $ 在 $ (0,+\mathrm{\infty }) $ 上单调递减,故 $ \mathrm{B} $ 错误;对于 $ \mathrm{C} $ , $ f(x)=-\dfrac{1}{x} $ 在 $ (0,+\mathrm{\infty }) $ 上单调递增,故 $ \mathrm{C} $ 正确;对于 $ \mathrm{D} $ ,因为 $ f(\dfrac{1}{2})={3}^{|\frac{1}{2}-1|}={3}^{\frac{1}{2}}=\sqrt{3} $ , $ f(1)={3}^{|1-1|}={3}^{0}=1 $ ,所以 $ f(x)={3}^{|x-1|} $ 在 $ (0,+\mathrm{\infty }) $ 上不单调递增, $ \mathrm{D} $ 错误.故选 $ \mathrm{C} $ .
17.设函数 $ f(x)=(x+a) \ln (x+b) $ .若 $ f(x)\geqslant 0 $ ,则 $ {a}^{2}+{b}^{2} $ 的最小值为( )
A. $ \dfrac{1}{8} $
B. $ \dfrac{1}{4} $
C. $ \dfrac{1}{2} $
D.1
答案:C
解析: $ f(x)=(x+a) \ln (x+b)\geqslant 0 $ 可看作 $ {f}_{1}(x)=x+a $ 与 $ {f}_{2}(x)= \ln (x+b) $ 在定义域 $ (-b,+\mathrm{\infty }) $ 内同正同负,因此两函数图象与 $ x $ 轴的交点重合,如图所示.

令 $ {f}_{1}(x)=x+a=0 $ , $ {f}_{2}(x)= \ln (x+b)=0 $ ,得 $ -a=1-b $ ,即 $ a-b+1=0 $ , $ {a}^{2}+{b}^{2}= (b-1)^{2}+{b}^{2}=2{b}^{2}-2b+1=2{\left(b-\dfrac{1}{2} \right) ^ {2}}+\dfrac{1}{2}\geqslant \dfrac{1}{2} $ ,所以 $ {a}^{2}+{b}^{2} $ 的最小值为 $ \dfrac{1}{2} $ ,故选 $ \mathrm{C} $ .
18.设函数 $ f(x)= \ln |2x+1|- \ln |2x-1| $ ,则 $ f(x) $ ( )
A.是偶函数,且在 $ (\dfrac{1}{2},+\mathrm{\infty }) $ 单调递增
B.是奇函数,且在 $ (-\dfrac{1}{2},\dfrac{1}{2}) $ 单调递减
C.是偶函数,且在 $ (-\mathrm{\infty },-\dfrac{1}{2}) $ 单调递增
D.是奇函数,且在 $ (-\mathrm{\infty },-\dfrac{1}{2}) $ 单调递减
答案:D
解析: $ f(x) $ 的定义域为 $ {x|x\ne ±\dfrac{1}{2}} $ ,且 $ f(-x)= \ln |-2x+1|- \ln |-2x-1|= \ln |2x-1|- \ln |2x+1|=-f(x) $ ,所以 $ f(x) $ 为奇函数.
当 $ x > 0 $ 时,
$ f(x)=\begin{cases} \ln (2x+1)- \ln (1-2x),0 < x < \dfrac{1}{2},\\ \ln (2x+1)- \ln (2x-1),x > \dfrac{1}{2}.\end{cases} $
当 $ 0 < x < \dfrac{1}{2} $ 时, $ f(x)= \ln \dfrac{2x+1}{1-2x}= \ln (-1-\dfrac{2}{2x-1}) $ ,易知 $ f(x) $ 在 $ (0,\dfrac{1}{2}) $ 上单调递增;当 $ x > \dfrac{1}{2} $ 时, $ f(x)= \ln \dfrac{2x+1}{2x-1}= \ln (1+\dfrac{2}{2x-1}) $ ,易知 $ f(x) $ 在 $ (\dfrac{1}{2},+\mathrm{\infty }) $ 上单调递减.
因为 $ f(x) $ 为奇函数,且在 $ (-\dfrac{1}{2} $ , $ \dfrac{1}{2}) $ 上连续,所以 $ f(x) $ 在 $ (-\dfrac{1}{2} $ , $ \dfrac{1}{2}) $ 上单调递增,在 $ (-\mathrm{\infty } $ , $ -\dfrac{1}{2}) $ 和 $ (\dfrac{1}{2} $ , $ +\mathrm{\infty }) $ 上单调递减,故选 $ \mathrm{D} $ .
19.已知函数 $ f (x )=\begin{cases}2-\mid x\mid ,x\leqslant 2,\\ (x-2)^{2},x > 2,\end{cases} $ 函数 $ g(x)=3-f(2-x) $ ,则函数 $ y=f(x)-g(x) $ 的零点个数为( )
A.2
B.3
C.4
D.5
答案:A
解析: $ f(2-x)=\begin{cases}2-\mid 2-x\mid ,x\geqslant 0,\\ {x}^{2},x < 0,\end{cases} $
从而 $ g(x)=\begin{cases}1+\mid 2-x\mid ,x\geqslant 0,\\ 3-{x}^{2},x < 0.\end{cases} $
在同一坐标系下画出 $ y=f(x) $ , $ y=g(x) $ 的图象,如图所示.
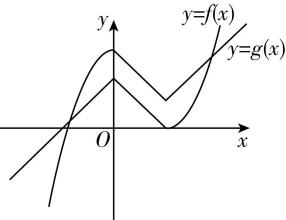
观察可得两函数图象有2个交点,从而函数 $ y=f(x)-g(x) $ 的零点个数为2.
20.已知函数 $ f(x)=| \lg x|-kx-2 $ ,给出下列四个结论:
①当 $ k=0 $ 时, $ f(x) $ 恰有2个零点;
②存在负数 $ k $ ,使得 $ f(x) $ 恰有1个零点;
③存在负数 $ k $ ,使得 $ f(x) $ 恰有3个零点;
④存在正数 $ k $ ,使得 $ f(x) $ 恰有3个零点.
其中所有正确结论的序号是 .
解析:令 $ f(x)=0 $ ,得 $ | \lg x|=kx+2 $ .对①,当 $ k=0 $ 时, $ | \lg x|=2 $ ,即 $ \lg x=2 $ 或 $ \lg x=-2 $ ,则 $ x=100 $ 或 $ x=\dfrac{1}{100} $ ,所以方程 $ | \lg x|=kx+2 $ 有两个不等实数根,即 $ f(x) $ 有2个零点,故①正确.
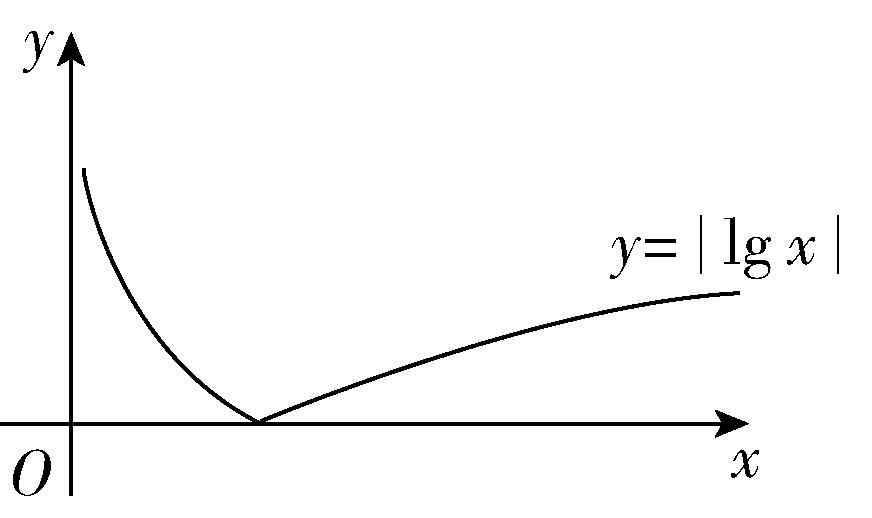
对②和③, $ f(x) $ 的零点个数即为函数 $ y=| \lg x| $ 与函数 $ y=kx+2 $ 图象的交点个数,画出函数 $ y=| \lg x| $ 的图象,如图, $ y=kx+2 $ 的图象过定点 $ (0,2) $ .当 $ k < 0 $ 时,由图象可以看出,当 $ y=kx+2 $ 与函数 $ y=| \lg x| $ 的图象相切时,两函数图象有一个公共点,即 $ \exists k < 0 $ ,使得 $ f(x) $ 有1个零点,而两函数图象最多有两个交点,所以当 $ k < 0 $ 时, $ f(x) $ 不可能有3个零点,故②正确,③错误;
当 $ k > 0 $ 时,由图象可以看出, $ y=kx+2 $ 与函数 $ y=| \lg x| $ 的图象可能有一个、两个或三个交点,所以 $ \exists k > 0 $ ,使得 $ f(x) $ 有3个零点,故④正确.正确的序号为①②④.
21.已知函数 $ f(x)=\begin{cases}{\mathrm{e}}^{x},x\leqslant 0,\\ \ln \text{ }x,x > 0,\end{cases}\text{ }g(x)=f(x)+x+a $ .若 $ g(x) $ 存在2个零点,则 $ a $ 的取值范围是( )
A. $ [-1,0) $
B. $ [0,+\mathrm{\infty }) $
C. $ [-1,+\mathrm{\infty }) $
D. $ [1,+\mathrm{\infty }) $
答案:C
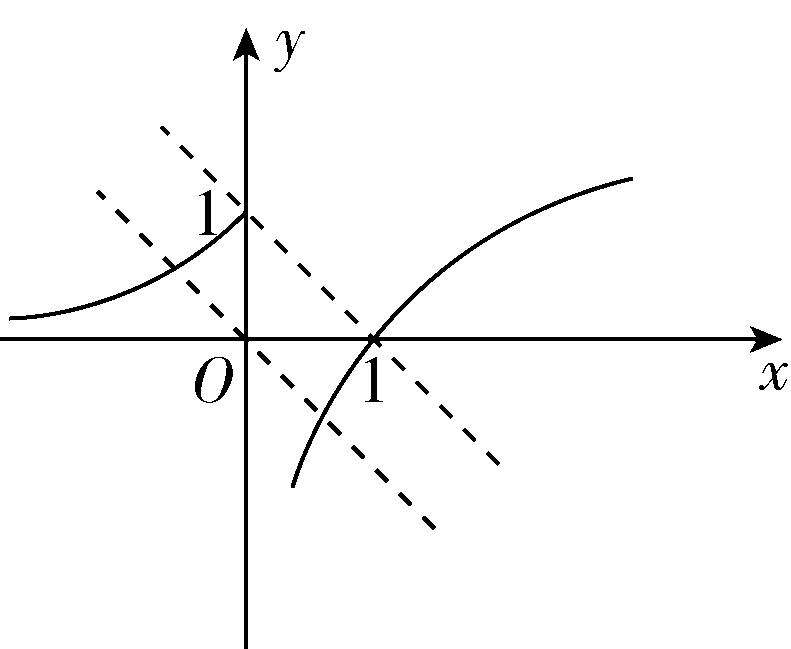
解析: $ \because $ 函数 $ g(x) $ 存在2个零点, $ \therefore $ 函数 $ y=f(x) $ 的图象与 $ y=-x-a $ 的图象有2个交点.
如图,平移直线 $ y=-x $ ,可以看出当且仅当 $ -a\leqslant 1 $ ,即 $ a\geqslant -1 $ 时,直线 $ y=-x-a $ 与 $ y=f(x) $ 的图象有2个交点.故选C.
22.已知函数 $ f(x)=\begin{cases}{x}^{3},x\geqslant 0,\\ -x,x < 0.\end{cases} $ 若函数 $ g(x)=f(x)-|k{x}^{2}-2x|(k\in \boldsymbol{R}) $ 恰有4个零点,则 $ k $ 的取值范围是( )
A. $ (-\mathrm{\infty },-\dfrac{1}{2})\cup (2\sqrt{2},+\mathrm{\infty }) $
B. $ (-\mathrm{\infty },-\dfrac{1}{2})\cup (0,2\sqrt{2}) $
C. $ (-\mathrm{\infty },0)\cup (0,2\sqrt{2}) $
D. $ (-\mathrm{\infty },0)\cup (2\sqrt{2},+\mathrm{\infty }) $
答案:D
解析:当 $ k=0 $ 时, $ g(x)=\begin{cases}{x}^{3}-2x,x\geqslant 0,\\ x,x < 0,\end{cases} $ 令 $ {x}^{3}-2x=0 $ ,得 $ x=0 $ , $ x=\sqrt{2} $ , $ x=-\sqrt{2} $ (舍),所以 $ g(x) $ 有2个零点,不符合题意.当 $ k > 0 $ 时,
$ g(x)=\begin{cases}{x}^{3}+(k{x}^{2}-2x),0\leqslant x\leqslant \dfrac{2}{k},\\ {x}^{3}-(k{x}^{2}-2x),x > \dfrac{2}{k},\\ -x-(k{x}^{2}-2x),x < 0,\end{cases} $
即 $ g(x)=\begin{cases}x({x}^{2}+kx-2),0\leqslant x\leqslant \dfrac{2}{k},\\ x({x}^{2}-kx+2),x > \dfrac{2}{k},\\ -x(kx-1),x < 0.\end{cases} $
当 $ x < 0 $ 时, $ -x(kx-1) < 0 $ , $ g(x) $ 无零点.
当 $ 0\leqslant x\leqslant \dfrac{2}{k} $ 时,设 $ ℎ(x)={x}^{2}+kx-2 $ ,因为 $ ℎ(0)=-2 < 0 $ , $ ℎ(\dfrac{2}{k})=\dfrac{4}{{k}^{2}} > 0 $ ,由函数零点存在定理可知, $ g(x) $ 在 $ (0,\dfrac{2}{k}) $ 上有1个零点,又 $ g(0)=0 $ ,所以 $ g(x) $ 在 $ [0 $ , $ \dfrac{2}{k} ] $ 上有2个零点.
若使 $ g(x) $ 有4个零点,则 $ {x}^{2}-kx+2=0 $ 在 $ (\dfrac{2}{k} $ , $ +\mathrm{\infty }) $ 上有2个不等实根.
设 $ s(x)={x}^{2}-kx+2 $ ,因为 $ s(\dfrac{2}{k})=\dfrac{4}{{k}^{2}} > 0 $ ,所以只需满足 $ \begin{cases}k > 0,\\ \dfrac{k}{2} > \dfrac{2}{k},\\ \mathrm{\Delta }={k}^{2}-8 > 0,\end{cases} $
解得 $ k > 2\sqrt{2} $ .
当 $ k < 0 $ 时,
$ g(x)=\begin{cases}{x}^{3}+(k{x}^{2}-2x),x\geqslant 0,\\ -x-(k{x}^{2}-2x),\dfrac{2}{k}\leqslant x < 0,\\ -x+(k{x}^{2}-2x),x < \dfrac{2}{k},\end{cases} $
即 $ g(x)=\begin{cases}x({x}^{2}+kx-2),x\geqslant 0,\\ -x(kx-1),\dfrac{2}{k}\leqslant x < 0,\\ x(kx-3),x < \dfrac{2}{k}.\end{cases} $
当 $ x < \dfrac{2}{k} $ 时,令 $ kx-3=0 $ ,得 $ x=\dfrac{3}{k} < \dfrac{2}{k} $ , $ g(x) $ 在 $ (-\mathrm{\infty },\dfrac{2}{k}) $ 上有1个零点;
当 $ \dfrac{2}{k}\leqslant x < 0 $ 时,令 $ kx-1=0 $ ,得 $ x=\dfrac{1}{k} $ , $ \dfrac{2}{k} < \dfrac{1}{k} < 0 $ ,所以 $ g(x) $ 在 $ [\dfrac{2}{k},0) $ 上有1个零点;
当 $ x\geqslant 0 $ 时,令 $ m(x)={x}^{2}+kx-2 $ .
因为函数 $ m(x) $ 图象的对称轴 $ x=-\dfrac{k}{2} > 0 $ , $ \mathrm{\Delta }={k}^{2}+8 > 0 $ , $ m(0)=-2 < 0 $ ,
所以 $ g(x) $ 在 $ (0,+\mathrm{\infty }) $ 上有1个零点,又 $ g(0)=0 $ ,
所以 $ g(x) $ 在 $ [0,+\mathrm{\infty }) $ 上有2个零点.
所以当 $ k < 0 $ 时, $ g(x) $ 有4个零点.
综上,若 $ g(x) $ 恰有4个零点,则 $ k < 0 $ 或 $ k > 2\sqrt{2} $ ,故选 $ \mathrm{D} $ .
23.设 $ a\in \boldsymbol{R} $ ,函数 $ f(x)=a{x}^{2}-2x-|{x}^{2}-ax+1| $ .若 $ f(x) $ 恰有两个零点,则 $ a $ 的取值范围为 .
答案: $ (-\mathrm{\infty },0)\cup (0,1)\cup (1,+\mathrm{\infty }) $
解析:令 $ {x}^{2}-ax+1=0 $ ,则 $ {\mathrm{\Delta }}_{1}={a}^{2}-4 $ ,
当 $ -2\leqslant a\leqslant 2 $ 时, $ {\mathrm{\Delta }}_{1}\leqslant 0 $ , $ {x}^{2}-ax+1\geqslant 0 $ 恒成立,此时 $ f(x)=(a-1){x}^{2}+(a-2)x-1 $ .
当 $ a\ne 1 $ 时,令 $ f(x)=(a-1){x}^{2}+(a-2)x-1=0 $ ,则 $ {\mathrm{\Delta }}_{2}={\left(a-2\right) ^ {2}}+4(a-1)={a}^{2} $ ,当 $ a\ne 0 $ 时, $ {\mathrm{\Delta }}_{2} > 0 $ , $ f(x) $ 有且仅有两个零点;
当 $ a=1 $ 时, $ f(x)=-x-1 $ , $ f(x) $ 有且仅有一个零点,不符合题意,
所以 $ -2\leqslant a < 0 $ 或 $ 0 < a < 1 $ 或 $ 1 < a\leqslant 2 $ .
当 $ a < -2 $ 或 $ a > 2 $ 时, $ {\mathrm{\Delta }}_{1} > 0 $ ,方程 $ {x}^{2}-ax+1=0 $ 有两个不等实根,设为 $ {x}_{1} $ , $ {x}_{2} $ , $ {x}_{1} < {x}_{2} $ ,
所以 $ f(x)=\begin{cases}[(a+1)x-1](x-1),{x}_{1}\leqslant x\leqslant {x}_{2},\\ [(a-1)x-1](x+1),x < {x}_{1}\mathrm{或}x > {x}_{2}.\end{cases} $
设 $ g(x)=[(a+1)x-1](x-1) $ ,令 $ g(x)=0 $ ,解得 $ x=1 $ 或 $ x=\dfrac{1}{a+1} $ ;设 $ ℎ(x)=[(a-1)x-1](x+1) $ ,令 $ ℎ(x)=0 $ ,解得 $ x=-1 $ 或 $ x=\dfrac{1}{a-1} $ .
当 $ a < -2 $ 时, $ {x}_{1}=\dfrac{a-\sqrt{{a}^{2}-4}}{2} < -1 $ , $ \dfrac{1}{a+1} < {x}_{2}=\dfrac{a+\sqrt{{a}^{2}-4}}{2} < \dfrac{1}{a-1} $ ,所以 $ f(x) $ 有且仅有两个零点,符合题意.
当 $ a > 2 $ 时,因为 $ {x}_{2}=\dfrac{a+\sqrt{{a}^{2}-4}}{2} > 1 $ ,且 $ \dfrac{1}{a+1} < {x}_{1}=\dfrac{a-\sqrt{{a}^{2}-4}}{2} < \dfrac{1}{a-1} $ ,
所以 $ f(x) $ 有且仅有两个零点,符合题意.
综上所述, $ a $ 的取值范围为 $ (-\mathrm{\infty },0)\cup (0,1)\cup (1,+\mathrm{\infty }) $ .
24.(多选)噪声污染问题越来越受到重视.用声压级来度量声音的强弱,定义声压级 $ {L}_{p}=20× \lg \dfrac{p}{{p}_{0}} $ ,其中常数 $ {p}_{0}({p}_{0} > 0) $ 是听觉下限阈值, $ p $ 是实际声压.下表为不同声源的声压级:
声源 | 与声源的距离/ $ \mathrm{m} $ | 声压级/ $ \mathrm{d}\mathrm{B} $ |
燃油汽车 | 10 | $ 60\sim 90 $ |
混合动力汽车 | 10 | $ 50\sim 60 $ |
电动汽车 | 10 | 40 |
已知在距离燃油汽车、混合动力汽车、电动汽车 $ 10\mathrm{m} $ 处测得实际声压分别为 $ {p}_{1} $ , $ {p}_{2} $ , $ {p}_{3} $ ,则( )(多选)
A. $ {p}_{1}\geqslant {p}_{2} $
B. $ {p}_{2} > 10{p}_{3} $
C. $ {p}_{3}=100{p}_{0} $
D. $ {p}_{1}\leqslant 100{p}_{2} $
答案:ACD
解析:由 $ {L}_{p}=20 \lg \dfrac{p}{{p}_{0}} $ ,对于燃油汽车 $ 60\leqslant 20 \lg \dfrac{{p}_{1}}{{p}_{0}}\leqslant 90 $ ,即 $ 3\leqslant \lg {p}_{1}- \lg {p}_{0}\leqslant \dfrac{9}{2} $ , $ \therefore \lg (1000{p}_{0})=3+ \lg {p}_{0}\leqslant \lg {p}_{1}\leqslant \dfrac{9}{2}+ \lg {p}_{0}= \lg ({10}^{\frac{9}{2}}{p}_{0}) $ ,即 $ 1000{p}_{0}\leqslant {p}_{1}\leqslant {10}^{\frac{9}{2}}{p}_{0} $ ;同理,对于混合动力汽车 $ {10}^{\frac{5}{2}}{p}_{0}\leqslant {p}_{2}\leqslant 1000{p}_{0} $ ;对于电动汽车 $ 20 \lg \dfrac{{p}_{3}}{{p}_{0}}=40 $ ,则 $ \lg {p}_{3}- \lg {p}_{0}=2 $ , $ \therefore \lg {p}_{3}=2+ \lg {p}_{0}= \lg (100{p}_{0}) $ , $ \therefore {p}_{3}=100{p}_{0} $ ,选项 $ \mathrm{C} $ 正确 $ {\rm .} {p}_{1}\geqslant {p}_{2} $ ,选项 $ \mathrm{A} $ 正确 $ {\rm .} 10{p}_{3}=1000{p}_{0} $ ,则 $ {p}_{2}\leqslant 10{p}_{3} $ ,选项 $ \mathrm{B} $ 错误 $ {\rm .} {10}^{\frac{9}{2}}{p}_{0}\leqslant 100{p}_{2}\leqslant {10}^{5}{p}_{0} $ ,则 $ {p}_{1}\leqslant 100{p}_{2} $ ,选项 $ \mathrm{D} $ 正确.故选 $ \mathrm{A}\mathrm{C}\mathrm{D} $ .
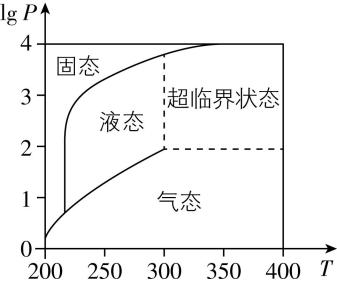
25.在北京冬奥会上,国家速滑馆“冰丝带”使用高效环保的二氧化碳跨临界直冷制冰技术,为实现绿色冬奥作出了贡献.如图描述了一定条件下二氧化碳所处的状态与 $ T $ 和 $ \lg P $ 的关系,其中 $ T $ 表示温度,单位是 $ \mathrm{K} $ ; $ P $ 表示压强,单位是 $ \mathrm{b}\mathrm{a}\mathrm{r} $ .下列结论中正确的是( )
A.当 $ T=220 $ , $ P=1026 $ 时,二氧化碳处于液态
B.当 $ T=270 $ , $ P=128 $ 时,二氧化碳处于气态
C.当 $ T=300 $ , $ P=9987 $ 时,二氧化碳处于超临界状态
D.当 $ T=360 $ , $ P=729 $ 时,二氧化碳处于超临界状态
答案:D
解析:对于 $ \mathrm{A} $ 选项,当 $ T=220 $ , $ P=1026 $ 时, $ \lg P= \lg 1026 > \lg {10}^{3}=3 $ ,根据题图可知,二氧化碳处于固态;
对于 $ \mathrm{B} $ 选项,当 $ T=270 $ , $ P=128 $ 时, $ \lg P= \lg 128\in (2,3) $ ,根据题图可知,二氧化碳处于液态;
对于 $ \mathrm{C} $ 选项,当 $ T=300 $ , $ P=9987 $ 时, $ \lg P= \lg 9987 < \lg {10}^{4}=4 $ ,且 $ \lg P $ 接近于4,根据题图可知,二氧化碳处于固态;
对于 $ \mathrm{D} $ 选项,当 $ T=360 $ , $ P=729 $ 时, $ \lg P= \lg 729\in (2,3) $ ,根据题图可知,二氧化碳处于超临界状态.
故选 $ \mathrm{D} $ .
26.青少年视力是社会普遍关注的问题,视力情况可借助视力表测量.通常用五分记录法和小数记录法记录视力数据,五分记录法的数据 $ L $ 和小数记录法的数据 $ V $ 满足 $ L=5+ \lg \text{ }V $ .已知某同学视力的五分记录法的数据为 $ 4.9 $ ,则其视力的小数记录法的数据约为 $ (\sqrt[10]{10}\approx 1.259) $ ( )
A.1.5
B.1.2
C.0.8
D.0.6
答案:C
解析:由 $ L=5+ \lg \text{ }V $ ,当 $ L=4.9 $ 时, $ \lg \text{ }V=-0.1 $ ,则 $ V={10}^{-0.1}={10}^{-\frac{1}{10}}=\dfrac{1}{\sqrt[10]{10}}\approx \dfrac{1}{1.259}\approx 0.8 $ .故选 $ \mathrm{C} $ .
二、刷原创
1.已知指数函数 $ f(x)={a}^{x} $ 为增函数,且图象过点 $ (\dfrac{1}{2}a $ , $ m) $ , $ (b,{m}^{b-1}) $ ,则 $ {2}^{a}+{4}^{b} $ 满足( )
A.当 $ b > 0 $ 时,有最大值 $ 25\sqrt{2} $
B.当 $ b < 0 $ 时,有最大值5
C.当 $ b > 0 $ 时,有最小值32
D.当 $ b < 0 $ 时,有最小值2
答案:C
解析:因为 $ f(x)={a}^{x} $ 为增函数,所以 $ a > 1 $ ,又 $ {a}^{\frac{a}{2}}=m $ , $ {a}^{b}={m}^{b-1} $ ,则 $ m > 1 $ , $ {a}^{b}=({a}^{\frac{a}{2}})^{b-1} $ , $ b=\dfrac{a}{2}(b-1) $ , $ b=1+\dfrac{2}{a-2}\in (-\mathrm{\infty },-1)\cup (1,+\mathrm{\infty }) $ ,
又 $ b=1+\dfrac{2}{a-2}=\dfrac{a}{a-2} $ ,取倒数后整理可得 $ \dfrac{2}{a}+\dfrac{1}{b}=1 $ .
$ a=\dfrac{2b}{b-1} $ ,则 $ {2}^{a}+{4}^{b}={4}^{\frac{b}{b-1}}+{4}^{b}=4({4}^{\frac{1}{b-1}}+{4}^{b-1}) $ ,当 $ b < 0 $ 时, $ b < -1 $ , $ b-1 < -2 $ ,故 $ {2}^{a}+{4}^{b}=4({4}^{\frac{1}{b-1}}+{4}^{b-1}) > 8×{2}^{\frac{1}{b-1}+b-1} $ ,由对勾函数的性质知 $ y=\dfrac{1}{b-1}+b-1 $ 在 $ (-\mathrm{\infty },-1) $ 上单调递增,故 $ {2}^{a}+{4}^{b} > \sqrt{2} $ .
又由于 $ y={4}^{b-1} $ 单调递增, $ y={4}^{\frac{1}{b-1}} $ 单调递减,且 $ 0 < {4}^{b-1} < \dfrac{1}{16} $ , $ \dfrac{1}{2} < {4}^{\frac{1}{b-1}} < 1 $ ,则 $ {2}^{a}+{4}^{b}=4({4}^{\frac{1}{b-1}}+{4}^{b-1}) < 4×(1+\dfrac{1}{16})=\dfrac{17}{4} $ , $ \mathrm{B} $ , $ \mathrm{D} $ 错误.当 $ b > 0 $ 时, $ b > 1 $ , $ b-1 > 0 $ ,故 $ {2}^{a}+{4}^{b}=4({4}^{\frac{1}{b-1}}+{4}^{b-1})\geqslant 8×{2}^{\frac{1}{b-1}+b-1}\geqslant 8×{2}^{2}=32 $ ,当且仅当 $ b=2 $ 时等号成立, $ \mathrm{A} $ 错误, $ \mathrm{C} $ 正确.故选 $ \mathrm{C} $ .
2.实数 $ {2}^{\sqrt{3}} $ , $ {3}^{\sqrt{2}} $ , $ {\mathrm{\pi }}^{\sqrt{5}} $ , $ {2}^{\mathrm{\pi }} $ 从小到大排列为 .
答案: $ {2}^{\sqrt{3}} < {3}^{\sqrt{2}} < {2}^{\mathrm{\pi }} < {\mathrm{\pi }}^{\sqrt{5}} $
解析:因为 $ {({3}^{\sqrt{2}})}^{\sqrt{6}}={9}^{\sqrt{3}} $ , $ {({2}^{\sqrt{3}})}^{\sqrt{6}}={8}^{\sqrt{2}} $ ,则由 $ y={x}^{\sqrt{3}} $ 在 $ (0,+\mathrm{\infty }) $ 上单调递增, $ y={8}^{x} $ 在 $ \boldsymbol{R} $ 上单调递增,知 $ {9}^{\sqrt{3}} > {8}^{\sqrt{3}} > {8}^{\sqrt{2}} $ ,故 $ {3}^{\sqrt{2}} > {2}^{\sqrt{3}} $ ,又由函数 $ f(x)={a}^{x}(a > 1) $ 为增函数,得 $ {3}^{\sqrt{2}} < {3}^{\frac{3}{2}}=\sqrt{27} < {2}^{3} < {2}^{\mathrm{\pi }} $ ,则 $ {2}^{\sqrt{3}} < {3}^{\sqrt{2}} < {2}^{\mathrm{\pi }} < {2}^{3.2}=8\cdot {2}^{\frac{1}{5}} < {\mathrm{\pi }}^{2}\cdot {\mathrm{\pi }}^{\frac{1}{5}}={\mathrm{\pi }}^{2.2} < {\mathrm{\pi }}^{\sqrt{5}} $ .
3.已知函数 $ f(x)=\begin{cases}\dfrac{2}{\sqrt{2-x}}-a\cdot {2}^{-x},x\leqslant 0,\\ { \log }_{\frac{1}{4}}x,x > 0.\end{cases} $
(1) 若 $ \forall {x}_{1}\in (-\mathrm{\infty },0] $ , $ \exists {x}_{2}\in [1,+\mathrm{\infty }) $ ,使得 $ f({x}_{1})=f({x}_{2}) $ ,求解关于 $ a $ 的方程 $ f(f(0))=0 $ ;
(2) 若函数 $ f(x) $ 的图象上存在关于直线 $ y=x $ 对称的点,求实数 $ a $ 的取值范围.
答案:(1) 【解】由题意知 $ {f(x)|x\leqslant 0}\subseteq {f(x)|x\geqslant 1} $ ,因为 $ y={ \log }_{\frac{1}{4}}x $ 为减函数,所以 $ {f(x)|x\geqslant 1}=(-\mathrm{\infty },0] $ .若 $ a\leqslant 0 $ ,则 $ x\leqslant 0 $ 时, $ 0 < \dfrac{2}{\sqrt{2-x}}\leqslant \sqrt{2} $ , $ -a\cdot {2}^{-x}\geqslant 0 $ ,与 $ {f(x)|x\leqslant 0}\subseteq (-\mathrm{\infty },0] $ 矛盾,不符合题意,故 $ a > 0 $ .
当 $ a > 0 $ 时, $ y=\dfrac{2}{\sqrt{2-x}}-a\cdot {2}^{-x} $ 在 $ (-\mathrm{\infty },0] $ 上单调递增,故在 $ x=0 $ 处取得最大值,即 $ f(0)=\sqrt{2}-a\leqslant 0 $ ,则 $ a\geqslant \sqrt{2} $ .要使 $ f(f(0))=0 $ ,即 $ f(\sqrt{2}-a)=0 $ ,因为 $ \sqrt{2}-a\leqslant 0 $ ,当 $ x\leqslant 0 $ 时, $ f(x) $ 的最大值为0,且在 $ x=0 $ 处取得,故 $ \sqrt{2}-a=0 $ ,即 $ a=\sqrt{2} $ .
所以关于 $ a $ 的方程 $ f(f(0))=0 $ 的解集为{ $ \sqrt{2} $ }.
(2) 因为曲线 $ y={ \log }_{\frac{1}{4}}x $ 关于直线 $ y=x $ 对称的曲线为 $ y={\left(\dfrac{1}{4}\right) ^ {x}} $ ,所以函数 $ f(x) $ 的图象上若存在关于直线 $ y=x $ 对称的点,则曲线 $ y={\left(\dfrac{1}{4}\right) ^ {x}} $ 与 $ y=\dfrac{2}{\sqrt{2-x}}-a\cdot {2}^{-x} $ 的图象在 $ (-\mathrm{\infty },0] $ 上有公共点,
故 $ \exists x\in (-\mathrm{\infty },0] $ ,使 $ {\left(\dfrac{1}{4}\right) ^ {x}}=\dfrac{2}{\sqrt{2-x}}-a\cdot {2}^{-x} $ ,即 $ a=\dfrac{2\cdot {2}^{x}}{\sqrt{2-x}}-{2}^{-x} $ 在 $ x\in (-\mathrm{\infty },0] $ 上有解.
因为函数 $ y=\dfrac{2\cdot {2}^{x}}{\sqrt{2-x}} $ 在 $ (-\mathrm{\infty },0] $ 上单调递增,所以函数 $ g(x)=\dfrac{2\cdot {2}^{x}}{\sqrt{2-x}}-{2}^{-x} $ 在 $ (-\mathrm{\infty },0] $ 上单调递增,当 $ x\to -\mathrm{\infty } $ 时, $ g(x)\to -\mathrm{\infty } $ ,当 $ x=0 $ 时, $ g(0)=\sqrt{2}-1 $ .
所以 $ a\leqslant \sqrt{2}-1 $ ,即 $ a $ 的取值范围为 $ (-\mathrm{\infty },\sqrt{2}-1] $ .
解析:













