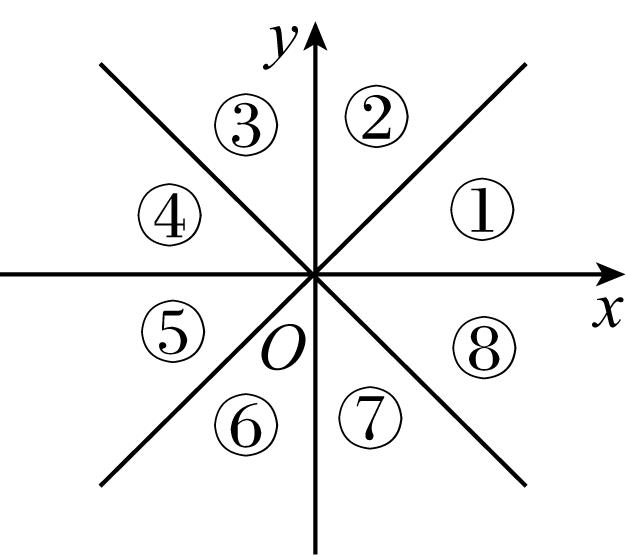
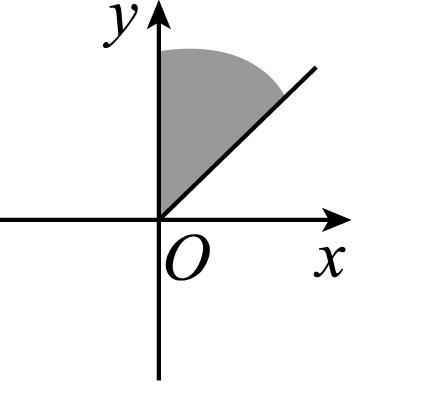
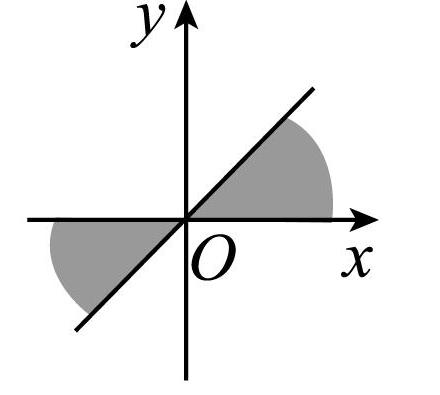
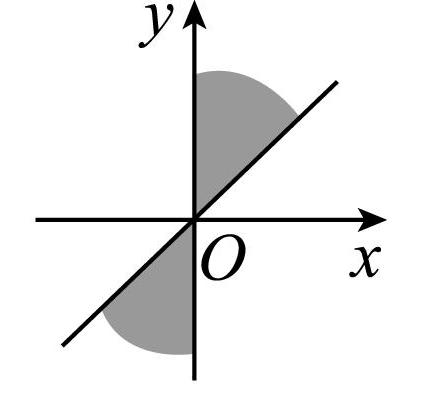
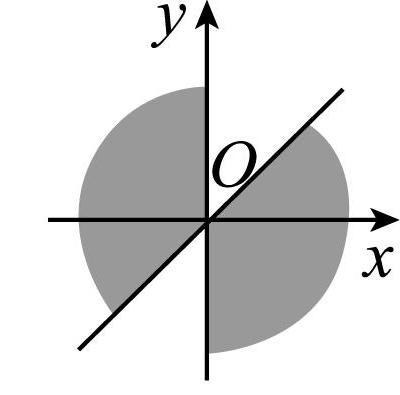
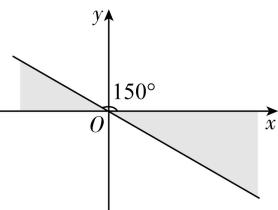
6.如图,终边落在阴影部分(包括边界)的角 $ \alpha $ 的集合是( )
A. $ {\alpha |{150}^{\circ }+k\cdot {360}^{\circ }\leqslant \alpha \leqslant {180}^{\circ }+k\cdot {360}^{\circ } $ , $ k\in \boldsymbol{Z} $ }
B. $ {\alpha |{150}^{\circ }+k\cdot {180}^{\circ }\leqslant \alpha \leqslant {180}^{\circ }+k\cdot {180}^{\circ } $ , $ k\in \boldsymbol{Z} $ }
C. $ {\alpha |-{210}^{\circ }+k\cdot {360}^{\circ }\leqslant \alpha \leqslant -{180}^{\circ }+k\cdot {360}^{\circ } $ , $ k\in \mathrm{Z} $ }
D. $ {\alpha |-{30}^{\circ }+k\cdot {360}^{\circ }\leqslant \alpha \leqslant k\cdot {360}^{\circ } $ , $ k\in \boldsymbol{Z} $ }
终边落在阴影部分的角 $ \alpha $ 满足 $ {150}^{\circ }+k\cdot {180}^{\circ }\leqslant \alpha \leqslant {180}^{\circ }+k\cdot {180}^{\circ } $ , $ k\in \boldsymbol{Z} $ ,即终边落在阴影部分(包括边界)的角 $ \alpha $ 的集合是 $ {\alpha |{150}^{\circ }+k\cdot {180}^{\circ }\leqslant \alpha \leqslant {180}^{\circ }+k\cdot {180}^{\circ } $ , $ k\in \boldsymbol{Z} $ }.故选 $ \mathrm{B} $ .