5.1.2 弧度制
一、刷基础
1.(多选)下列说法正确的是( )(多选)
A. $ {240}^{\circ }=\dfrac{4\mathrm{\pi }}{3} $
B.1弧度的角比 $ {1}^{\circ } $ 的角大
C.用弧度制量角时,角的大小与圆的半径有关
D.扇形的周长为 $ 6\mathrm{c}\mathrm{m} $ ,面积为 $ 2{\mathrm{c}\mathrm{m}}^{2} $ ,则扇形的圆心角的弧度数为4
答案:AB
解析:对于 $ \mathrm{A} $ , $ {240}^{\circ }=\dfrac{240}{180}\mathrm{\pi }=\dfrac{4\mathrm{\pi }}{3} $ ,故 $ \mathrm{A} $ 正确;
对于 $ \mathrm{B} $ , $ 1\mathrm{r}\mathrm{a}\mathrm{d}={(\dfrac{180}{\mathrm{\pi }})}^{\circ } > {1}^{\circ } $ ,故 $ \mathrm{B} $ 正确;
对于 $ \mathrm{C} $ ,用弧度制量角时,角的大小与圆的半径无关,故 $ \mathrm{C} $ 错误;
对于 $ \mathrm{D} $ ,设扇形的圆心角为 $ \alpha $ ,半径为 $ R $ ,
因为扇形的周长为 $ 6\mathrm{c}\mathrm{m} $ ,面积为 $ 2{\mathrm{c}\mathrm{m}}^{2} $ ,
所以 $ \begin{cases}\alpha R+2R=6,\\ \dfrac{1}{2}\alpha {R}^{2}=2,\end{cases} $ 解得 $ \begin{cases}R=2,\\ \alpha =1\end{cases} $ 或 $ \begin{cases}R=1,\\ \alpha =4,\end{cases} $ 即扇形的圆心角的弧度数为4或1,故 $ \mathrm{D} $ 错误.故选 $ \mathrm{A}\mathrm{B} $ .
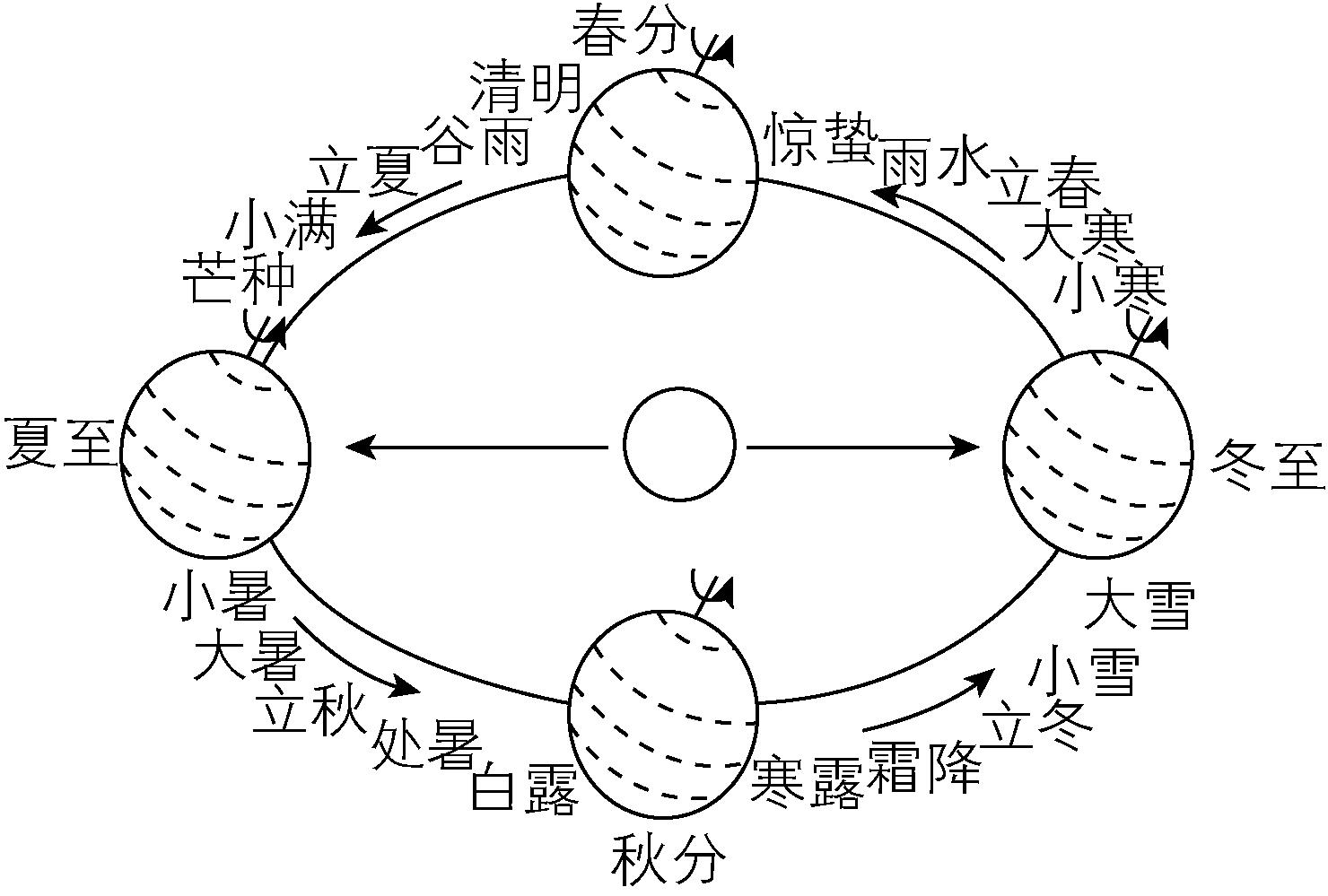
2.现行的二十四节气是根据地球在黄道(即地球绕太阳公转的轨道)上的位置变化而制定的,每个节气对应地球在黄道上运动 $ {15}^{\circ } $ 所到达的一个位置.根据描述,从立冬到立春对应地球在黄道上运动所对圆心角的弧度数为( )
A. $ -\dfrac{\mathrm{\pi }}{3} $
B. $ \dfrac{\mathrm{\pi }}{3} $
C. $ \dfrac{5\mathrm{\pi }}{12} $
D. $ \dfrac{\mathrm{\pi }}{2} $
答案:D
解析:根据题意,从立冬到立春对应地球在黄道上运动所对圆心角的度数为 $ 6×{15}^{\circ }={90}^{\circ } $ ,即弧度数为 $ \dfrac{\mathrm{\pi }}{2} $ .故选 $ \mathrm{D} $ .
3.若圆弧长度等于圆内接正三角形的边长,则其圆心角的弧度数为( )
A. $ \dfrac{\mathrm{\pi }}{6} $
B. $ \dfrac{\mathrm{\pi }}{3} $
C.3
D. $ \sqrt{3} $
答案:D
解析:如图,等边三角形 $ ABC $ 是半径为 $ r $ 的圆 $ O $ 的内接三角形,
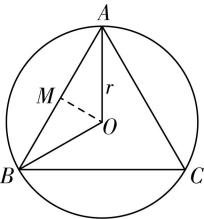
则线段 $ AB $ 所对的圆心角 $ \mathrm{\angle }AOB=\dfrac{2\mathrm{\pi }}{3} $ ,
作 $ OM\perp AB $ ,垂足为 $ M $ ,
在 $ \mathrm{R}\mathrm{t}△AOM $ 中, $ AO=r $ , $ \mathrm{\angle }AOM=\dfrac{\mathrm{\pi }}{3} $ ,
所以 $ AM=\dfrac{\sqrt{3}}{2}r $ , $ AB=\sqrt{3}r $ .
故圆弧长度 $ l=\sqrt{3}r $ ,
所以长度等于圆内接正三角形的边长的圆弧所对圆心角的弧度数为 $ \alpha =\dfrac{l}{r}=\sqrt{3} $ ,故选 $ \mathrm{D} $ .
4.体操中有“前空翻转体540度”这样的动作名称,则 $ {540}^{\circ } $ 化成弧度是( )
A. $ \dfrac{3\mathrm{\pi }}{2} $
B. $ 3\mathrm{\pi } $
C. $ \dfrac{5\mathrm{\pi }}{2} $
D. $ \dfrac{13\mathrm{\pi }}{6} $
答案:B
解析: $ {540}^{\circ }=540×\dfrac{\mathrm{\pi }}{180}=3\mathrm{\pi } $ .故选 $ \mathrm{B} $ .
5.(多选)将下列角度与弧度进行互化,正确的有( )(多选)
A. $ \dfrac{511}{6}\mathrm{\pi }=1{530}^{\circ } $
B. $ -\dfrac{7\mathrm{\pi }}{12}=-{105}^{\circ } $
C. $ {10}^{\circ }=\dfrac{\mathrm{\pi }}{18} $
D. $ -{855}^{\circ }=-\dfrac{19\mathrm{\pi }}{4} $
答案:BCD
解析:对于 $ \mathrm{A} $ , $ \dfrac{511}{6}\mathrm{\pi }=\dfrac{511}{6}×{180}^{\circ }=15{330}^{\circ } $ ,故 $ \mathrm{A} $ 错误;
对于 $ \mathrm{B} $ , $ -\dfrac{7\mathrm{\pi }}{12}=-\dfrac{7}{12}×{180}^{\circ }=-{105}^{\circ } $ ,故 $ \mathrm{B} $ 正确;
对于 $ \mathrm{C} $ , $ {10}^{\circ }=10×\dfrac{\mathrm{\pi }}{180}=\dfrac{\mathrm{\pi }}{18} $ ,故 $ \mathrm{C} $ 正确;
对于 $ \mathrm{D} $ , $ -{855}^{\circ }=-855×\dfrac{\mathrm{\pi }}{180}=-\dfrac{19\mathrm{\pi }}{4} $ ,故 $ \mathrm{D} $ 正确.故选 $ \mathrm{B}\mathrm{C}\mathrm{D} $ .
6.已知 $ \alpha ={15}^{\circ } $ , $ \beta =\dfrac{\mathrm{\pi }}{10} $ , $ \gamma =1 $ , $ \theta ={105}^{\circ } $ , $ \varphi =\dfrac{7\mathrm{\pi }}{12} $ ,则 $ \alpha $ , $ \beta $ , $ \gamma $ , $ \theta $ , $ \varphi $ 的大小关系为 .
答案: $ \alpha < \beta < \gamma < \theta =\varphi $
解析:(化为弧度) $ \text{:}\alpha ={15}^{\circ }=15×\dfrac{\mathrm{\pi }}{180}=\dfrac{\mathrm{\pi }}{12} $ , $ \theta ={105}^{\circ }=105×\dfrac{\mathrm{\pi }}{180}=\dfrac{7\mathrm{\pi }}{12} $ .
显然 $ \dfrac{\mathrm{\pi }}{12} < \dfrac{\mathrm{\pi }}{10} < 1 < \dfrac{7\mathrm{\pi }}{12} $ ,故 $ \alpha < \beta < \gamma < \theta =\varphi $ .
7.(多选)下列各组角终边相同的一组是( )(多选)
A. $ -{30}^{\circ } $ , $ {330}^{\circ } $
B. $ -{120}^{\circ } $ , $ {960}^{\circ } $
C. $ \dfrac{11}{6}\mathrm{\pi } $ , $ -\dfrac{7}{6}\mathrm{\pi } $
D. $ \dfrac{9}{17}\mathrm{\pi } $ , $ -\dfrac{25}{17}\mathrm{\pi } $
答案:ABD
解析:对于A,因为 $ -{30}^{\circ }=-{360}^{\circ }+{330}^{\circ } $ ,所以 $ -{30}^{\circ } $ 与 $ {330}^{\circ } $ 角的终边相同,故A正确;
对于B, $ -{120}^{\circ }=-{360}^{\circ }+{240}^{\circ } $ , $ {960}^{\circ }=2×{360}^{\circ }+{240}^{\circ } $ ,
所以 $ -{120}^{\circ } $ 与 $ {960}^{\circ } $ 角的终边相同,故B正确;
对于C, $ -\dfrac{7}{6}\mathrm{\pi }=-2\mathrm{\pi }+\dfrac{5}{6}\mathrm{\pi } $ ,即 $ -\dfrac{7}{6}\mathrm{\pi } $ 角的终边与 $ \dfrac{5}{6}\mathrm{\pi } $ 角的终边相同,
$ \dfrac{11}{6}\mathrm{\pi }\in [0,2\mathrm{\pi }) $ , $ \dfrac{5}{6}\mathrm{\pi }\in [0,2\mathrm{\pi }) $ ,所以 $ \dfrac{11}{6}\mathrm{\pi } $ 角与 $ \dfrac{5}{6}\mathrm{\pi } $ 角的终边不相同,
即 $ \dfrac{11}{6}\mathrm{\pi } $ 与 $ -\dfrac{7}{6}\mathrm{\pi } $ 角的终边不相同,故C错误;
对于D, $ -\dfrac{25}{17}\mathrm{\pi }=-2\mathrm{\pi }+\dfrac{9}{17}\mathrm{\pi } $ ,所以 $ \dfrac{9}{17}\mathrm{\pi } $ 与 $ -\dfrac{25}{17}\mathrm{\pi } $ 角的终边相同,故D正确.故选 $ \mathrm{A}\mathrm{B}\mathrm{D} $ .
8.如果角 $ \alpha $ 与角 $ \gamma +\dfrac{\mathrm{\pi }}{3} $ 的终边相同,角 $ \beta $ 与角 $ \gamma -\dfrac{\mathrm{\pi }}{3} $ 的终边相同,那么 $ \alpha -\beta $ 的可能值为( )(多选)
A. $ \dfrac{2\mathrm{\pi }}{3} $
B. $ 2\mathrm{\pi } $
C. $ \dfrac{20\mathrm{\pi }}{3} $
D. $ 20\mathrm{\pi } $
答案:AC
解析:角 $ \alpha $ 与角 $ \gamma +\dfrac{\mathrm{\pi }}{3} $ 的终边相同,则 $ \alpha =m\cdot 2\mathrm{\pi }+\gamma +\dfrac{\mathrm{\pi }}{3} $ , $ m\in \boldsymbol{Z} $ ,
角 $ \beta $ 与角 $ \gamma -\dfrac{\mathrm{\pi }}{3} $ 的终边相同,则 $ \beta =n\cdot 2\mathrm{\pi }+\gamma -\dfrac{\mathrm{\pi }}{3} $ , $ n\in \boldsymbol{Z} $ ,
$ \therefore \alpha -\beta =m\cdot 2\mathrm{\pi }+\gamma +\dfrac{\mathrm{\pi }}{3}-(n\cdot 2\mathrm{\pi }+\gamma -\dfrac{\mathrm{\pi }}{3})=(m-n)\cdot 2\mathrm{\pi }+\dfrac{2\mathrm{\pi }}{3} $ , $ m $ , $ n\in \boldsymbol{Z} $ ,
即角 $ \alpha -\beta $ 与角 $ \dfrac{2\mathrm{\pi }}{3} $ 的终边相同,选项 $ \mathrm{A} $ , $ \mathrm{C} $ 符合题意.故选 $ \mathrm{A}\mathrm{C} $ .
9.下列说法正确的是( )
A.终边在 $ x $ 轴上的角的集合是 $ {\alpha |\alpha =\dfrac{k\mathrm{\pi }}{2},k\in \boldsymbol{Z}} $
B.若角 $ \alpha $ 的终边在第二象限,则角 $ \alpha $ 是钝角
C.若角 $ \alpha $ 是钝角,则角 $ \alpha $ 的终边在第二象限
D.终边在直线 $ y=-x $ 上的角的集合是 $ {\alpha |\alpha =\dfrac{\mathrm{\pi }}{4}+k\mathrm{\pi },k\in \boldsymbol{Z}} $
答案:C
解析:对于 $ \mathrm{A} $ ,终边在 $ x $ 轴上的角的集合是 $ {\alpha |\alpha =k\mathrm{\pi } $ , $ k\in \boldsymbol{Z} $ },故 $ \mathrm{A} $ 错误;
对于 $ \mathrm{B} $ ,终边在第二象限的角未必都是钝角,例如 $ \alpha =2\mathrm{\pi }+\dfrac{3\mathrm{\pi }}{4} $ ,故 $ \mathrm{B} $ 错误;
对于 $ \mathrm{C} $ ,因为钝角是大于 $ \dfrac{\mathrm{\pi }}{2} $ 且小于 $ \mathrm{\pi } $ 的角,所以钝角必在第二象限,故 $ \mathrm{C} $ 正确;
对于 $ \mathrm{D} $ ,终边在直线 $ y=-x $ 上的角的集合是 $ {\alpha |\alpha =\dfrac{3\mathrm{\pi }}{4}+k\mathrm{\pi } $ , $ k\in \boldsymbol{Z}} $ ,故 $ \mathrm{D} $ 错误.故选 $ \mathrm{C} $ .
10.终边在直线 $ y=x $ 上的角 $ \alpha $ 构成的集合可以表示为 .(用弧度制表示)
答案: $ {\alpha |\alpha =k\mathrm{\pi }+\dfrac{\mathrm{\pi }}{4},k\in \boldsymbol{Z}} $
解析: $ \because $ 角 $ \alpha $ 的终边在直线 $ y=x $ 上, $ \therefore $ 角 $ \alpha $ 的终边在第一、三象限的角平分线上.
$ \because $ 终边在第一象限的角平分线上的一个角为 $ \dfrac{\mathrm{\pi }}{4} $ ,
$ \therefore $ 终边在直线 $ y=x $ 上的角 $ \alpha $ 构成的集合可以表示为 $ {\alpha |\alpha =k\mathrm{\pi }+\dfrac{\mathrm{\pi }}{4},k\in \boldsymbol{Z}} $ .
11.已知半径为3的圆弧所对的圆心角为 $ \dfrac{\mathrm{\pi }}{6} $ ,则该圆弧所在的扇形面积为( )
A. $ \sqrt{3}\mathrm{\pi } $
B. $ \dfrac{\mathrm{\pi }}{3} $
C. $ \dfrac{2\mathrm{\pi }}{3} $
D. $ \dfrac{3\mathrm{\pi }}{4} $
答案:D
解析:由题意,扇形面积为 $ S=\dfrac{1}{2}\alpha {r}^{2}=\dfrac{1}{2}×\dfrac{\mathrm{\pi }}{6}×{3}^{2}=\dfrac{3\mathrm{\pi }}{4} $ .故选 $ \mathrm{D} $ .
12.(多选)小夏同学在学习了任意角和弧度制的知识后,对家里的扇形瓷器盘产生了浓厚的兴趣,并临摹出该瓷器盘的大致形状,如图所示.在扇形 $ OAB $ 中, $ \mathrm{\angle }AOB=\dfrac{\mathrm{\pi }}{3} $ , $ OB=OA=2 $ ,则( )
 (多选)
(多选)
A. $ \mathrm{\angle }AOB={30}^{\circ } $
B. $ \stackrel{⌢}{AB} $ 的长为 $ \dfrac{2\mathrm{\pi }}{3} $
C.扇形 $ OAB $ 的周长为 $ \dfrac{2\mathrm{\pi }}{3}+4 $
D.扇形 $ OAB $ 的面积为 $ \dfrac{4\mathrm{\pi }}{3} $
答案:BC
解析:因为 $ \mathrm{\angle }AOB=\dfrac{\mathrm{\pi }}{3}={60}^{\circ } $ ,所以 $ \mathrm{A} $ 错误;
$ \stackrel{⌢}{AB} $ 的长 $ l=\alpha r=\dfrac{\mathrm{\pi }}{3}×2=\dfrac{2\mathrm{\pi }}{3} $ ,所以 $ \mathrm{B} $ 正确;
扇形 $ OAB $ 的周长为 $ \dfrac{2\mathrm{\pi }}{3}+4 $ ,所以 $ \mathrm{C} $ 正确;
扇形 $ OAB $ 的面积为 $ S=\dfrac{1}{2}lr=\dfrac{1}{2}×\dfrac{2\mathrm{\pi }}{3}×2=\dfrac{2\mathrm{\pi }}{3}(l $ 为弧 $ AB $ 的长度 $ ) $ ,所以 $ \mathrm{D} $ 错误.故选 $ \mathrm{B}\mathrm{C} $ .
13.已知扇形的圆心角是 $ \alpha $ ,半径是 $ r $ ,弧长为 $ l $ .
(1) 若 $ \alpha ={100}^{\circ } $ , $ r=2 $ ,求扇形的面积;
(2) 若扇形的周长为20,求扇形面积的最大值,并求此时扇形圆心角的弧度数.
答案:(1) 【解】因为 $ \alpha ={100}^{\circ }=100×\dfrac{\mathrm{\pi }}{180}=\dfrac{5\mathrm{\pi }}{9} $ ,
所以扇形的面积 $ S=\dfrac{1}{2}lr=\dfrac{1}{2}\alpha {r}^{2}=\dfrac{1}{2}×\dfrac{5\mathrm{\pi }}{9}×4=\dfrac{10\mathrm{\pi }}{9} $ .
(2) 【解】由题意可知 $ l+2r=20 $ ,即 $ l=20-2r $ ,
所以扇形的面积 $ S=\dfrac{1}{2}lr=\dfrac{1}{2}(20-2r)\cdot $ $ r=-{\left(r-5\right) ^ {2}}+25 $ ,
易知当 $ r=5 $ 时,扇形的面积最大,最大值为25,
此时 $ l=20-2×5=10 $ , $ \alpha =\dfrac{l}{r}=\dfrac{10}{5}=2 $ .
解析:
14.(多选)下列与 $ \dfrac{9\mathrm{\pi }}{4} $ 的终边相同的角的表达式中,正确的是( )(多选)
A. $ {45}^{\circ }+2k\mathrm{\pi }(k\in \boldsymbol{Z}) $
B. $ \dfrac{9\mathrm{\pi }}{4}+k\cdot {360}^{\circ }(k\in \boldsymbol{Z}) $
C. $ -{315}^{\circ }+k\cdot {360}^{\circ }(k\in \boldsymbol{Z}) $
D. $ \dfrac{\mathrm{\pi }}{4}+2k\mathrm{\pi }(k\in \boldsymbol{Z}) $
答案:CD
解析:对于 $ \mathrm{A} $ , $ \mathrm{B} $ ,在同一个表达式中,角度制与弧度制不能混用,所以 $ \mathrm{A} $ , $ \mathrm{B} $ 错误.
对于 $ \mathrm{C} $ , $ \dfrac{9\mathrm{\pi }}{4}=4\mathrm{\pi }-\dfrac{7\mathrm{\pi }}{4} $ ,则角 $ \dfrac{9\mathrm{\pi }}{4} $ 与 $ -\dfrac{7\mathrm{\pi }}{4} $ 的终边相同,且 $ -\dfrac{7\mathrm{\pi }}{4} $ 化角度制为 $ -{315}^{\circ } $ ,则角 $ -{315}^{\circ } $ 与 $ \dfrac{9\mathrm{\pi }}{4} $ 的终边相同,故 $ -{315}^{\circ }+k\cdot {360}^{\circ }(k\in \boldsymbol{Z}) $ 是与 $ \dfrac{9\mathrm{\pi }}{4} $ 的终边相同的角的表达式,故 $ \mathrm{C} $ 正确;
对于 $ \mathrm{D} $ ,由 $ \dfrac{9\mathrm{\pi }}{4}=2\mathrm{\pi }+\dfrac{\mathrm{\pi }}{4} $ ,得 $ \dfrac{9\mathrm{\pi }}{4} $ 与 $ \dfrac{\mathrm{\pi }}{4} $ 的终边相同,则与 $ \dfrac{9\mathrm{\pi }}{4} $ 终边相同的角可以写成 $ \dfrac{\mathrm{\pi }}{4}+2k\mathrm{\pi }(k\in \boldsymbol{Z}) $ 的形式,故 $ \mathrm{D} $ 正确.故选 $ \mathrm{C}\mathrm{D} $ .
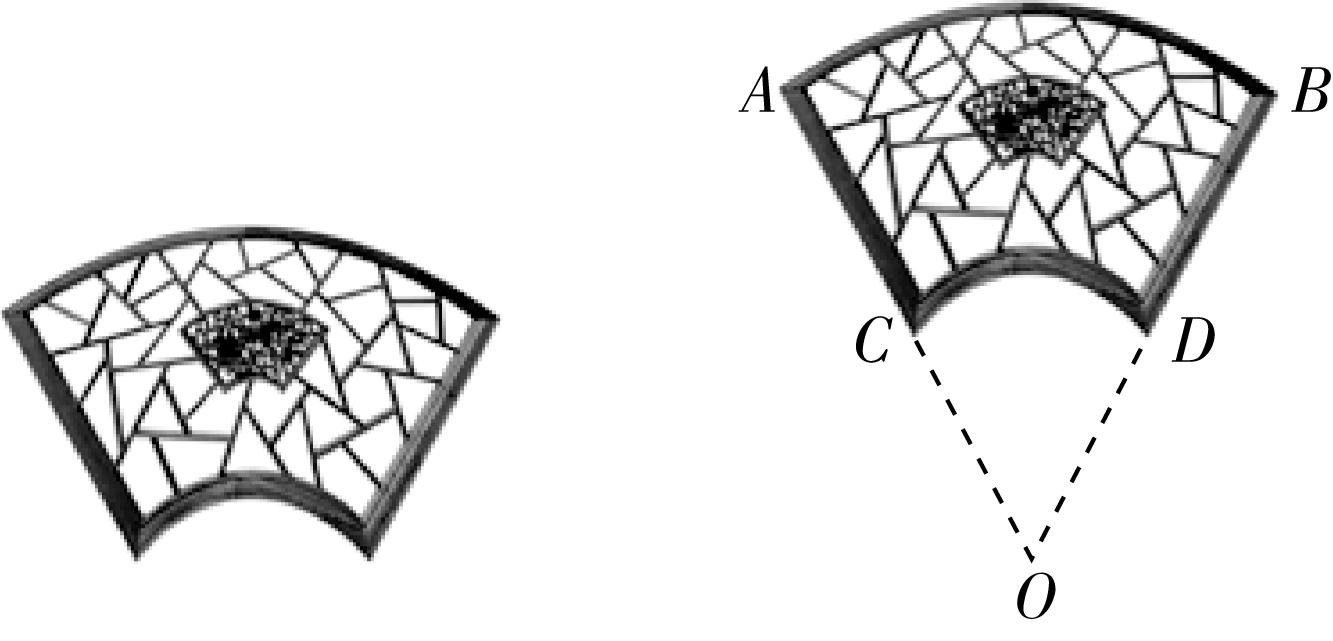
15.扇子最早称“翣”,其功能并不是纳凉,而是礼仪用具,后用于纳凉、娱乐、欣赏等.扇文化是中国传统文化的重要门类,扇子的美学也随之融入到建筑等艺术审美之中.图①为一古代扇形窗子,此窗子所在扇形的半径(图②) $ AO=80\mathrm{c}\mathrm{m} $ ,圆心角为 $ {45}^{\circ } $ ,且 $ C $ 为 $ AO $ 的中点,则该扇形窗子的面积为( )
图① 图②
A. $ 10\text{ }800{\mathrm{c}\mathrm{m}}^{2} $
B. $ 10\text{ }800\mathrm{\pi }\text{ }{\mathrm{c}\mathrm{m}}^{2} $
C. $ 600\mathrm{\pi }\text{ }{\mathrm{c}\mathrm{m}}^{2} $
D. $ 600\text{ }{\mathrm{c}\mathrm{m}}^{2} $
答案:C
解析:由题意得 $ {45}^{\circ } $ 化为弧度为 $ \dfrac{\mathrm{\pi }}{4} $ ,又 $ AO=80\text{ }\mathrm{c}\mathrm{m} $ , $ C $ 为 $ AO $ 的中点,则该扇形窗子的面积为 $ \dfrac{1}{2}×\dfrac{\mathrm{\pi }}{4}(O{A}^{2}-O{C}^{2})=\dfrac{1}{2}×\dfrac{\mathrm{\pi }}{4}({80}^{2}-{40}^{2})=600\mathrm{\pi }({\mathrm{c}\mathrm{m}}^{2}) $ ,故选 $ \mathrm{C} $ .
16.圆心角为 $ {36}^{\circ } $ 的扇形的弧长为 $ \dfrac{4\mathrm{\pi }}{5} $ ,则该扇形面积为 .
答案: $ \dfrac{8\mathrm{\pi }}{5} $
解析:设扇形的半径为 $ R $ ,
因为 $ {36}^{\circ }=\dfrac{\mathrm{\pi }}{5}\mathrm{r}\mathrm{a}\mathrm{d} $ ,圆心角为 $ {36}^{\circ } $ 的扇形的弧长为 $ \dfrac{4\mathrm{\pi }}{5} $ ,所以 $ \dfrac{\mathrm{\pi }}{5}R=\dfrac{4\mathrm{\pi }}{5} $ ,解得 $ R=4 $ ,
故扇形的面积 $ S=\dfrac{1}{2}×\dfrac{4\mathrm{\pi }}{5}×4=\dfrac{8\mathrm{\pi }}{5} $ .
17.已知集合 $ M={x|x=\dfrac{k\mathrm{\pi }}{2}+\dfrac{\mathrm{\pi }}{4},k\in \boldsymbol{Z}} $ , $ N={x|x=\dfrac{k\mathrm{\pi }}{4}+\dfrac{\mathrm{\pi }}{2} $ , $ k\in \boldsymbol{Z}} $ ,则有( )
A. $ M=N $
B. $ M⫋N $
C. $ M⫋N $
D. $ M\cap N=\mathrm{⌀} $
答案:C
解析:因为集合 $ M $ 表示终边在第一、三象限或第二、四象限的角平分线上的角的集合,集合 $ \mathbf{N} $ 表示终边在坐标轴(四个位置)上和在第一、三象限或第二、四象限的角平分线上的角的集合,故 $ M⫋N $ .
18.已知扇形的周长为 $ 10\text{ }\mathrm{c}\mathrm{m} $ ,面积为 $ 4\text{ }{\mathrm{c}\mathrm{m}}^{2} $ ,则扇形的圆心角 $ \alpha $ 的弧度数为 .
解析:设扇形的半径为 $ r\text{ }\mathrm{c}\mathrm{m} $ ,圆心角 $ \alpha $ 所对的弧长为 $ l\text{ }\mathrm{c}\mathrm{m} $ .由题意得 $ \begin{cases}l+2r=10,\\ \dfrac{1}{2}lr=4,\end{cases} $ 解得 $ \begin{cases}l=8,\\ r=1\end{cases} $ 或 $ \begin{cases}l=2,\\ r=4,\end{cases}\therefore \alpha =8 $ 或 $ \alpha =\dfrac{1}{2} $ .又 $ \because 0 < \alpha < 2\mathrm{\pi } $ , $ \therefore \alpha =\dfrac{1}{2} $ .


 (多选)
(多选)