5.2.1三角函数的概念
一、刷基础
1.已知点 $ P(m,1) $ 是角 $ \alpha $ 终边上的一点,且 $ \sin \mathrm{ }\alpha =\dfrac{1}{3} $ ,则 $ m $ 的值为( )
A.2
B. $ -2\sqrt{2} $
C. $ -2\sqrt{2} $ 或2
D. $ -2\sqrt{2} $ 或 $ 2\sqrt{2} $
答案:D
解析:由三角函数定义可得 $ \sin \mathrm{ }\alpha =\dfrac{1}{\sqrt{{m}^{2}+{1}^{2}}}=\dfrac{1}{3} $ ,解得 $ m=±2\sqrt{2} $ ,所以 $ m $ 的值为 $ -2\sqrt{2} $ 或 $ 2\sqrt{2} $ .故选 $ \mathrm{D} $ .
2.(多选)已知角 $ \alpha $ 的终边上一点 $ P $ 的坐标为 $ (-1,\sqrt{5}) $ ,则( )(多选)
A. $ \alpha $ 为第四象限角
B. $ \sin \alpha =\dfrac{\sqrt{30}}{6} $
C. $ \cos \alpha =-\dfrac{\sqrt{6}}{6} $
D. $ \tan \alpha =\sqrt{5} $
答案:BC
解析:由题意得 $ \alpha $ 为第二象限角, $ \sin \alpha =\dfrac{\sqrt{5}}{\sqrt{1+5}}=\dfrac{\sqrt{30}}{6} $ , $ \cos \alpha =\dfrac{-1}{\sqrt{1+5}}=-\dfrac{\sqrt{6}}{6} $ , $ \tan \alpha =-\sqrt{5} $ .故选 $ \mathrm{B}\mathrm{C} $ .
3.在平面直角坐标系 $ xOy $ 中,一个质点在半径为2的圆 $ O $ 上,以圆 $ O $ 与 $ x $ 轴正半轴的交点 $ {P}_{0} $ 为起点,沿逆时针方向匀速运动到 $ P $ 点,每 $ 5\mathrm{s} $ 转一圈,则 $ 2\mathrm{s} $ 后 $ {P}_{0}P $ 的长为( )
A. $ 2 \sin \dfrac{2\mathrm{\pi }}{5} $
B. $ 2 \cos \dfrac{2\mathrm{\pi }}{5} $
C. $ 4 \sin \dfrac{2\mathrm{\pi }}{5} $
D. $ 4 \cos \dfrac{2\mathrm{\pi }}{5} $
答案:C
解析:由题意可知,一个质点在圆 $ O $ 上每 $ 5\mathrm{s} $ 逆时针转一圈, $ 2\mathrm{s} $ 后,到达 $ P $ 点,所以 $ \mathrm{\angle }PO{P}_{0}=\dfrac{4\mathrm{\pi }}{5} $ ,而在 $ △PO{P}_{0} $ 中, $ OP=O{P}_{0}=2 $ 且为圆的半径,取 $ {P}_{0}P $ 的中点 $ T $ ,连接 $ OT $ ,如图,
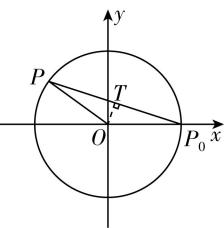
则 $ \mathrm{\angle }POT=\dfrac{2\mathrm{\pi }}{5} $ ,所以 $ \sin \mathrm{\angle }POT=\dfrac{PT}{OP}= \sin \dfrac{2\mathrm{\pi }}{5} $ ,则 $ PT=\dfrac{1}{2}P{P}_{0}=2 \sin \dfrac{2\mathrm{\pi }}{5} $ ,所以 $ P{P}_{0}=4 \sin \dfrac{2\mathrm{\pi }}{5} $ ,故选 $ \mathrm{C} $ .
4.(多选)给出下列各三角函数值,其中符号为负的是( )(多选)
A. $ \cos \mathrm{\pi } $
B. $ \cos (-{220}^{\circ }) $
C. $ \sin (-{100}^{\circ }) $
D. $ \tan 10 $
答案:ABC
解析:对 $ \mathrm{A} $ , $ \cos \mathrm{\pi }=-1 $ ,故 $ \mathrm{A} $ 正确;
对 $ \mathrm{B} $ , $ \cos (-{220}^{\circ })= \cos {140}^{\circ } < 0 $ ,故 $ \mathrm{B} $ 正确;
对 $ \mathrm{C} $ , $ \sin (-{100}^{\circ }) < 0 $ ,故 $ \mathrm{C} $ 正确;
对 $ \mathrm{D} $ ,因为 $ 3\mathrm{\pi } < 10 < \dfrac{7\mathrm{\pi }}{2} $ ,所以 $ \tan 10 > 0 $ ,故 $ \mathrm{D} $ 错误.
故选 $ \mathrm{A}\mathrm{B}\mathrm{C} $ .
5.“角 $ \theta $ 为第二象限角”是“ $ \sin \theta \cdot \cos \theta < 0 $ ”的( )
A.充分不必要条件
B.必要不充分条件
C.充要条件
D.既不充分也不必要条件
答案:A
解析:当角 $ \theta $ 为第二象限角时, $ \sin \theta > 0 $ , $ \cos \theta < 0 $ ,所以 $ \sin \theta \cdot \cos \theta < 0 $ ,充分性成立;
反过来,当 $ \sin \theta \cdot \cos \theta < 0 $ 时,角 $ \theta $ 为第二或第四象限角,必要性不成立.
所以“角 $ \theta $ 为第二象限角”是“ $ \sin \theta \cdot \cos \theta < 0 $ ”的充分不必要条件,故选 $ \mathrm{A} $ .
6.若 $ \alpha $ 是第四象限角,则点 $ P( \sin \alpha , \cos \alpha ) $ 在( )
A.第一象限
B.第二象限
C.第三象限
D.第四象限
答案:B
解析:由于 $ \alpha $ 是第四象限角,所以 $ \sin \alpha < 0 $ , $ \cos \alpha > 0 $ ,所以 $ P( \sin \alpha , \cos \alpha ) $ 在第二象限.故选 $ \mathrm{B} $ .
7.(多选)下列选项中,结果为正数的有( )(多选)
A. $ \sin 1+ \cos 1 $
B. $ \sin 2+ \cos 2 $
C. $ \sin 3+ \cos 3 $
D. $ \sin 4+ \cos 4 $
答案:AB
解析:由 $ 0 < 1 < \dfrac{\mathrm{\pi }}{2} $ ,可得 $ \sin 1 > 0 $ , $ \cos 1 > 0 $ ,所以 $ \sin 1+ \cos 1 > 0 $ ,所以 $ \mathrm{A} $ 正确;
由 $ \dfrac{\mathrm{\pi }}{2} < 2 < \dfrac{3\mathrm{\pi }}{4} < 3 < \mathrm{\pi } $ ,可得 $ \sin 2 > 0 $ , $ \sin 3 > 0 $ , $ \cos 2 < 0 $ , $ \cos 3 < 0 $ ,且 $ | \sin 2| > | \cos 2| $ , $ | \sin 3| < | \cos 3| $ ,所以 $ \sin 2+ \cos 2 > 0 $ , $ \sin 3+ \cos 3 < 0 $ ,所以 $ \mathrm{B} $ 正确, $ \mathrm{C} $ 错误;
由 $ \mathrm{\pi } < 4 < \dfrac{3\mathrm{\pi }}{2} $ ,可得 $ \sin 4 < 0 $ , $ \cos 4 < 0 $ ,所以 $ \sin 4+ \cos 4 < 0 $ ,所以 $ \mathrm{D} $ 错误.故选 $ \mathrm{A}\mathrm{B} $ .
8.(多选)有下列说法,其中错误的是( )(多选)
A.终边相同的角的同名三角函数值相等
B.同名三角函数值相等的角也相等
C.终边不相同,它们的同名三角函数值一定不相等
D.不相等的角,同名三角函数值也不相等
答案:BCD
解析:对于 $ \mathrm{A} $ ,由诱导公式一可知 $ \mathrm{A} $ 正确;
对于 $ \mathrm{B} $ , $ \sin {30}^{\circ }= \sin {150}^{\circ }=\dfrac{1}{2} $ ,但 $ {30}^{\circ }\ne {150}^{\circ } $ ,所以 $ \mathrm{B} $ 错误;
对于 $ \mathrm{C} $ ,如 $ \alpha ={60}^{\circ } $ , $ \beta ={120}^{\circ } $ 的终边不相同,但 $ \sin {60}^{\circ }= \sin {120}^{\circ }=\dfrac{\sqrt{3}}{2} $ ,所以 $ \mathrm{C} $ 错误;
对于 $ \mathrm{D} $ ,由 $ \mathrm{C} $ 中的例子可知 $ \mathrm{D} $ 错误.
9.下列不等式错误的是( )
A. $ \cos (-\dfrac{2\mathrm{\pi }}{5}) < 0 $
B. $ \sin \dfrac{13\mathrm{\pi }}{8} < 0 $
C. $ \tan {556}^{\circ } > 0 $
D. $ \sin {321}^{\circ } \cos {123}^{\circ } > 0 $
答案:A
解析:结合三角函数值在各象限的符号可知, $ \mathrm{A} $ 选项, $ \cos (-\dfrac{2\mathrm{\pi }}{5}) > 0 $ , $ \mathrm{A} $ 错误;
$ \mathrm{B} $ 选项, $ \sin \dfrac{13\mathrm{\pi }}{8}= \sin (2\mathrm{\pi }-\dfrac{3\mathrm{\pi }}{8})= \sin (-\dfrac{3\mathrm{\pi }}{8}) < 0 $ , $ \mathrm{B} $ 正确;
$ \mathrm{C} $ 选项, $ \tan {556}^{\circ }= \tan ({360}^{\circ }+{196}^{\circ })= \tan {196}^{\circ } > 0 $ , $ \mathrm{C} $ 正确;
$ \mathrm{D} $ 选项, $ \sin {321}^{\circ } \cos {123}^{\circ }= \sin ({360}^{\circ }-{39}^{\circ }) \cos {123}^{\circ }= \sin (-{39}^{\circ }) \cos {123}^{\circ } > 0 $ , $ \mathrm{D} $ 正确.故选 $ \mathrm{A} $ .
10. $ \sin {810}^{\circ }+ \tan {765}^{\circ }+ \tan 1{125}^{\circ }+ \cos {360}^{\circ }= $ .
解析:原式 $ = \sin (2×{360}^{\circ }+{90}^{\circ })+ \tan (2×{360}^{\circ }+{45}^{\circ })+ \tan (3×{360}^{\circ }+{45}^{\circ })+ \cos ({0}^{\circ }+{360}^{\circ })= \sin {90}^{\circ }+ \tan {45}^{\circ }+ \tan {45}^{\circ }+ \cos {0}^{\circ }=4 $ .
11.若角 $ \alpha $ 的终边落在直线 $ x+y=0 $ 上,则 $ \dfrac{ \sin \alpha }{\sqrt{1-{ \sin }^{2}\alpha }}+\dfrac{\sqrt{1-{ \cos }^{2}\alpha }}{ \cos \alpha }= $ ( )
A. 0
B. $ -2 $
C. 2
D. $ -2 $ 或2
答案:A
解析:若角 $ \alpha $ 的终边落在直线 $ x+y=0 $ 上,则 $ \begin{cases} \sin \alpha =\dfrac{\sqrt{2}}{2},\\ \cos \alpha =-\dfrac{\sqrt{2}}{2}\end{cases} $ 或 $ \begin{cases} \sin \alpha =-\dfrac{\sqrt{2}}{2},\\ \cos \alpha =\dfrac{\sqrt{2}}{2},\end{cases} $ 分别代入 $ \dfrac{ \sin \alpha }{\sqrt{1-{ \sin }^{2}\alpha }}+\dfrac{\sqrt{1-{ \cos }^{2}\alpha }}{ \cos \alpha } $ 中可得其值为0.
12.已知角 $ \alpha $ 的始边与 $ x $ 轴非负半轴重合,终边经过点 $ P(1,x) $ ,且 $ \sin \alpha =\dfrac{\sqrt{3}}{2} $ ,则 $ x= $ ( )
A. $ ±\sqrt{3} $
B. $ \sqrt{3} $
C. $ \dfrac{\sqrt{3}}{3} $
D. $ \dfrac{\sqrt{3}}{2} $
答案:B
解析:因为角 $ \alpha $ 的始边与 $ x $ 轴非负半轴重合,终边经过点 $ P(1,x) $ ,且 $ \sin \alpha =\dfrac{\sqrt{3}}{2} $ ,所以 $ \sin \alpha =\dfrac{x}{\sqrt{{1}^{2}+{x}^{2}}}=\dfrac{\sqrt{3}}{2}(x > 0) $ ,化简得 $ {x}^{2}=3 $ .
因为 $ x > 0 $ ,所以 $ x=\sqrt{3} $ .故选 $ \mathrm{B} $ .
