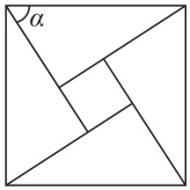
5.我国古代数学家赵爽在注解《周髀算经》一书时介绍了“赵爽弦图”,如图所示,它是由四个全等的直角三角形与一个小正方形拼成的大正方形,记直角三角形中较大的锐角为 $ \alpha $ ,大正方形的边长为 $ a $ ,小正方形的边长为 $ b $ ,若 $ \dfrac{ \sin \alpha (1-2 \sin \alpha \cos \alpha )}{ \sin \alpha - \cos \alpha }=\dfrac{2}{5} $ ,则 $ \dfrac{b}{a}= $ ( )
A. $ \dfrac{\sqrt{5}}{5} $
B. $ \dfrac{2\sqrt{5}}{5} $
C. $ \dfrac{1}{2} $
D. $ \dfrac{2}{3} $
由题意可得 $ \dfrac{ \sin \alpha (1-2 \sin \alpha \cos \alpha )}{ \sin \alpha - \cos \alpha } $
$ =\dfrac{ \sin \alpha ({ \sin }^{2}\alpha +{ \cos }^{2}\alpha -2 \sin \alpha \cos \alpha )}{ \sin \alpha - \cos \alpha } $
$ =\dfrac{ \sin \alpha ( \sin \alpha - \cos \alpha )^{2}}{ \sin \alpha - \cos \alpha } $
$ = \sin \alpha ( \sin \alpha - \cos \alpha ) $
$ =\dfrac{{ \sin }^{2}\alpha - \sin \alpha \cos \alpha }{{ \sin }^{2}\alpha +{ \cos }^{2}\alpha } $
$ =\dfrac{{ \tan }^{2}\alpha - \tan \alpha }{{ \tan }^{2}\alpha +1}=\dfrac{2}{5} $ ,
解得 $ \tan \alpha =2 $ 或 $ \tan \alpha =-\dfrac{1}{3} $ (舍去).
因为 $ \alpha $ 是直角三角形中较大的锐角,所以 $ \dfrac{\mathrm{\pi }}{4} < \alpha < \dfrac{\mathrm{\pi }}{2} $ ,
所以 $ \cos \alpha =\dfrac{1}{\sqrt{1+{ \tan }^{2}\alpha }}=\dfrac{\sqrt{5}}{5} $ , $ \sin \alpha = \tan \alpha \cdot \cos \alpha =\dfrac{2\sqrt{5}}{5} $ .
易知直角三角形的两条直角边分别为 $ a \sin \alpha $ , $ a \cos \alpha $ ,则 $ b=a \sin \alpha -a \cos \alpha $ ,
所以 $ \dfrac{b}{a}= \sin \alpha - \cos \alpha =\dfrac{2\sqrt{5}}{5}-\dfrac{\sqrt{5}}{5}=\dfrac{\sqrt{5}}{5} $ .故选 $ \mathrm{A} $ .