5.3 诱导公式
一、刷基础
1.(多选)下列选项各函数值符号为正的是( )(多选)
A. $ \sin 1{000}^{\circ } $
B. $ \tan (-2{100}^{\circ }) $
C. $ \sin (-7) $
D. $ \dfrac{ \sin \dfrac{7\mathrm{\pi }}{10} \cos \mathrm{\pi }}{ \tan \dfrac{17\mathrm{\pi }}{9}} $
答案:BD
解析:对于 $ \mathrm{A} $ , $ \sin 1{000}^{\circ }= \sin (2×{360}^{\circ }+{280}^{\circ })= \sin {280}^{\circ } $ ,因为 $ {270}^{\circ } < {280}^{\circ } < {360}^{\circ } $ ,所以 $ {280}^{\circ } $ 为第四象限角,所以 $ \sin 1{000}^{\circ }= \sin {280}^{\circ } < 0 $ ,故 $ \mathrm{A} $ 错误;
对于 $ \mathrm{B} $ , $ \tan (-2{100}^{\circ })=- \tan 2{100}^{\circ }=- \tan (11×{180}^{\circ }+{120}^{\circ })=- \tan {120}^{\circ } $ ,因为 $ {90}^{\circ } < {120}^{\circ } < {180}^{\circ } $ ,所以 $ {120}^{\circ } $ 为第二象限角,所以 $ \tan (-2{100}^{\circ })=- \tan {120}^{\circ } > 0 $ ,故 $ \mathrm{B} $ 正确;
对于 $ \mathrm{C} $ , $ \sin (-7)=- \sin 7 $ ,因为 $ 2\mathrm{\pi } < 7 < \dfrac{5\mathrm{\pi }}{2} $ ,所以7为第一象限角,所以 $ \sin (-7)=- \sin 7 < 0 $ ,故 $ \mathrm{C} $ 错误;
对于 $ \mathrm{D} $ , $ \dfrac{ \sin \dfrac{7\mathrm{\pi }}{10} \cos \mathrm{\pi }}{ \tan \dfrac{17\mathrm{\pi }}{9}}=\dfrac{- \sin \dfrac{7\mathrm{\pi }}{10}}{ \tan (2\mathrm{\pi }-\dfrac{\mathrm{\pi }}{9})}=\dfrac{- \sin (\mathrm{\pi }-\dfrac{3\mathrm{\pi }}{10})}{- \tan \dfrac{\mathrm{\pi }}{9}}=\dfrac{ \sin \dfrac{3\mathrm{\pi }}{10}}{ \tan \dfrac{\mathrm{\pi }}{9}} $ ,
因为 $ 0 < \dfrac{3\mathrm{\pi }}{10} < \dfrac{\mathrm{\pi }}{2} $ , $ 0 < \dfrac{\mathrm{\pi }}{9} < \dfrac{\mathrm{\pi }}{2} $ ,所以 $ \dfrac{3\mathrm{\pi }}{10} $ 为第一象限角, $ \dfrac{\mathrm{\pi }}{9} $ 为第一象限角,所以 $ \sin \dfrac{3\mathrm{\pi }}{10} > 0 $ , $ \tan \dfrac{\mathrm{\pi }}{9} > 0 $ ,
故 $ \dfrac{ \sin \dfrac{7\mathrm{\pi }}{10} \cos \mathrm{\pi }}{ \tan \dfrac{17\mathrm{\pi }}{9}}=\dfrac{ \sin \dfrac{3\mathrm{\pi }}{10}}{ \tan \dfrac{\mathrm{\pi }}{9}} > 0 $ ,故 $ \mathrm{D} $ 正确.故选 $ \mathrm{B}\mathrm{D} $ .
2.已知 $ x\in \boldsymbol{R} $ ,则下列等式恒成立的是( )(多选)
A. $ \sin (3\mathrm{\pi }-x)= \sin \text{ }x $
B. $ \sin \text{ }\dfrac{\mathrm{\pi }-x}{2}= \cos \text{ }\dfrac{x}{2} $
C. $ \cos (\dfrac{5\mathrm{\pi }}{2}+3x)= \sin \text{ }3x $
D. $ \cos (\dfrac{3\mathrm{\pi }}{2}+2x)=- \sin \text{ }2x $
答案:AB
解析: $ \sin (3\mathrm{\pi }-x)= \sin (\mathrm{\pi }-x)= \sin \text{ }x $ , $ \sin \dfrac{\mathrm{\pi }-x}{2}= \sin (\dfrac{\mathrm{\pi }}{2}-\dfrac{x}{2})= \cos \dfrac{x}{2} $ ,
$ \cos (\dfrac{5\mathrm{\pi }}{2}+3x)= \cos (\dfrac{\mathrm{\pi }}{2}+3x)=- \sin \text{ }3x $ ,
$ \text{ } \cos (\dfrac{3\mathrm{\pi }}{2}+2x)= \sin \text{ }2x $ ,故选 $ \mathrm{A}\mathrm{B} $ .
3.设 $ A $ , $ B $ , $ C $ 分别是 $ △ABC $ 的三个内角,则( )
A. $ \cos (A+B)= \cos C $
B. $ \cos \dfrac{A+B}{2}= \cos \dfrac{C}{2} $
C. $ \sin (A+B)= \sin C $
D. $ \sin \dfrac{A+B}{2}= \sin \dfrac{C}{2} $
答案:C
解析: $ \mathrm{A}. \cos (A+B)= \cos (\mathrm{\pi }-C)=- \cos C $ ,故 $ \mathrm{A} $ 错误.
$ \mathrm{B}. \cos \dfrac{A+B}{2}= \cos \dfrac{\mathrm{\pi }-C}{2}= \cos (\dfrac{\mathrm{\pi }}{2}-\dfrac{C}{2})= \sin \dfrac{C}{2} $ ,故 $ \mathrm{B} $ 错误.
$ \mathrm{C}. \sin (A+B)= \sin (\mathrm{\pi }-C)= \sin C $ ,故 $ \mathrm{C} $ 正确.
$ \mathrm{D}. \sin \dfrac{A+B}{2}= \sin \dfrac{\mathrm{\pi }-C}{2}= \sin (\dfrac{\mathrm{\pi }}{2}-\dfrac{C}{2})= \cos \dfrac{C}{2} $ ,故 $ \mathrm{D} $ 错误.故选 $ \mathrm{C} $ .
4. $ \tan {570}^{\circ }+ \sin {300}^{\circ }= $ ( )
A. $ \dfrac{5\sqrt{3}}{6} $
B. $ \dfrac{\sqrt{3}}{6} $
C. $ -\dfrac{\sqrt{3}}{6} $
D. $ -\dfrac{5\sqrt{3}}{6} $
答案:C
解析: $ \tan {570}^{\circ }+ \sin {300}^{\circ } $
$ = \tan ({360}^{\circ }+{210}^{\circ })+ \sin ({360}^{\circ }-{60}^{\circ }) $
$ = \tan ({180}^{\circ }+{30}^{\circ })- \sin {60}^{\circ } $
$ = \tan {30}^{\circ }- \sin {60}^{\circ }=\dfrac{\sqrt{3}}{3}-\dfrac{\sqrt{3}}{2}=-\dfrac{\sqrt{3}}{6} $ .
故选 $ \mathrm{C} $ .
5. $ \cos {330}^{\circ }+ \sin (-{30}^{\circ })+ \tan \dfrac{8}{3}\mathrm{\pi }+ \cos {90}^{\circ }= $ .
答案: $ -\dfrac{\sqrt{3}+1}{2} $
解析: $ \cos {330}^{\circ }+ \sin (-{30}^{\circ })+ \tan \dfrac{8}{3}\mathrm{\pi }+ \cos {90}^{\circ }= \cos ({360}^{\circ }-{30}^{\circ })- \sin {30}^{\circ }+ \tan (3\mathrm{\pi }-\dfrac{\mathrm{\pi }}{3})+0= \cos {30}^{\circ }-\dfrac{1}{2}- \tan \dfrac{\mathrm{\pi }}{3}=\dfrac{\sqrt{3}}{2}-\dfrac{1}{2}-\sqrt{3}=-\dfrac{\sqrt{3}+1}{2} $ .
6. $ \sin {95}^{\circ }+ \cos {185}^{\circ }+ \tan {240}^{\circ }= $ .
解析:原式 $ = \sin ({90}^{\circ }+{5}^{\circ })+ \cos ({180}^{\circ }+{5}^{\circ })+ \tan ({180}^{\circ }+{60}^{\circ })= \cos {5}^{\circ }+(- \cos {5}^{\circ })+ \tan {60}^{\circ }= \tan {60}^{\circ }=\sqrt{3} $ .
7.已知角 $ \alpha $ 的终边上有一点 $ P(1,3) $ ,则 $ \cos (\dfrac{3\mathrm{\pi }}{2}-\alpha )+2 \cos (-\mathrm{\pi }+\alpha ) $ 的值为( )
A. $ \dfrac{\sqrt{10}}{10} $
B. $ \dfrac{\sqrt{10}}{2} $
C. $ -\dfrac{\sqrt{10}}{10} $
D. $ -\dfrac{\sqrt{10}}{2} $
答案:D
解析:因为角 $ \alpha $ 的终边上有一点 $ P(1,3) $ ,
所以 $ \sin \alpha =\dfrac{3}{\sqrt{{1}^{2}+{3}^{2}}}=\dfrac{3}{\sqrt{10}}=\dfrac{3}{10}\sqrt{10} $ , $ \cos \alpha =\dfrac{1}{\sqrt{{1}^{2}+{3}^{2}}}=\dfrac{1}{\sqrt{10}}=\dfrac{\sqrt{10}}{10} $ ,
所以 $ \cos (\dfrac{3\mathrm{\pi }}{2}-\alpha )+2 \cos (-\mathrm{\pi }+\alpha )=- \sin \alpha -2 \cos \alpha =-\dfrac{3}{10}\sqrt{10}-\dfrac{2}{10}\sqrt{10}=-\dfrac{\sqrt{10}}{2} $ .故选 $ \mathrm{D} $ .
8.已知 $ \cos ({37}^{\circ }+\alpha )=\dfrac{1}{3} $ ,且 $ {0}^{\circ } < \alpha < {90}^{\circ } $ ,则 $ \tan ({37}^{\circ }+\alpha ){ \sin }^{2}({53}^{\circ }-\alpha )- \cos ({143}^{\circ }-\alpha )= $ ( )
A. $ \dfrac{3+\sqrt{2}}{9} $
B. $ \dfrac{3-\sqrt{2}}{9} $
C. $ \dfrac{3+2\sqrt{2}}{9} $
D. $ \dfrac{3-2\sqrt{2}}{9} $
答案:C
解析:因为 $ {0}^{\circ } < \alpha < {90}^{\circ } $ , $ \cos ({37}^{\circ }+\alpha )=\dfrac{1}{3} > 0 $ ,故 $ {37}^{\circ } < {37}^{\circ }+\alpha < {90}^{\circ } $ ,
令 $ {37}^{\circ }+\alpha =m $ ,则 $ m $ 为锐角,
因为 $ \cos m=\dfrac{1}{3} $ ,所以 $ \sin m=\dfrac{2\sqrt{2}}{3} $ ,且 $ \alpha =m-{37}^{\circ } $ ,
所以 $ \tan ({37}^{\circ }+\alpha ){ \sin }^{2}({53}^{\circ }-\alpha )- \cos ({143}^{\circ }-\alpha ) $
$ = \tan m{ \sin }^{2}({90}^{\circ }-m)- \cos ({180}^{\circ }-m) $
$ = \tan m{ \cos }^{2}m+ \cos m= \sin m \cos m+ \cos m $
$ =\dfrac{3+2\sqrt{2}}{9} $ .故选 $ \mathrm{C} $ .
9.已知 $ \cos (\dfrac{\mathrm{\pi }}{3}-\theta )=\dfrac{4}{5} $ ,则 $ \sin (\dfrac{2\mathrm{\pi }}{3}+\theta )= $ .
解析:令 $ t=\dfrac{\mathrm{\pi }}{3}-\theta $ ,则 $ \theta =\dfrac{\mathrm{\pi }}{3}-t $ , $ \cos t=\dfrac{4}{5} $ , $ \sin (\dfrac{\mathrm{\pi }}{3}-\theta )= \sin t=±\sqrt{1-{ \cos }^{2}t}=±\dfrac{3}{5} $ .
$ \therefore \sin (\dfrac{2\mathrm{\pi }}{3}+\theta )= \sin (\dfrac{2\mathrm{\pi }}{3}+\dfrac{\mathrm{\pi }}{3}-t)= \sin (\mathrm{\pi }-t)= \sin t=±\dfrac{3}{5} $ .
10.化简 $ \sqrt{1+2 \sin (\mathrm{\pi }-2) \cos (\mathrm{\pi }+2)} $ 的结果是( )
A. $ \sin 2+ \cos 2 $
B. $ \sin 2- \cos 2 $
C. $ \cos 2- \sin 2 $
D. $ - \sin 2- \cos 2 $
答案:B
解析:因为 $ \dfrac{\mathrm{\pi }}{2} < 2 < \dfrac{3\mathrm{\pi }}{4} $ ,所以 $ \sin 2 > 0 $ , $ \cos 2 < 0 $ ,则 $ \sin 2- \cos 2 > 0 $ ,
所以 $ \sqrt{1+2 \sin (\mathrm{\pi }-2) \cos (\mathrm{\pi }+2)} $
$ =\sqrt{1+2 \sin 2\cdot (- \cos 2)} $
$ =\sqrt{{ \sin }^{2}2-2 \sin 2 \cos 2+{ \cos }^{2}2} $
$ =| \sin 2- \cos 2|= \sin 2- \cos 2 $ ,故选 $ \mathrm{B} $ .
11.(多选)已知下列等式的左右两边都有意义,则下列等式恒成立的是( )(多选)
A. $ \dfrac{ \cos x}{1+ \sin x}=\dfrac{1- \sin x}{ \cos x} $
B. $ \dfrac{1+{ \sin }^{2}x}{ \sin x \cos x}=\dfrac{1+2{ \tan }^{2}x}{ \tan x} $
C. $ \sin ({53}^{\circ }-x)= \cos ({37}^{\circ }+x) $
D. $ \sin ({60}^{\circ }-x)= \cos ({480}^{\circ }+x) $
答案:ABC
解析:对于 $ \mathrm{A} $ , $ \dfrac{ \cos x}{1+ \sin x}=\dfrac{ \cos x(1- \sin x)}{(1+ \sin x)(1- \sin x)}=\dfrac{ \cos x(1- \sin x)}{1-{ \sin }^{2}x}=\dfrac{ \cos x(1- \sin x)}{{ \cos }^{2}x}=\dfrac{1- \sin x}{ \cos x} $ ,故 $ \mathrm{A} $ 正确;
对于 $ \mathrm{B} $ , $ \dfrac{1+{ \sin }^{2}x}{ \sin x \cos x}=\dfrac{({ \sin }^{2}x+{ \cos }^{2}x)+{ \sin }^{2}x}{ \sin x \cos x}=\dfrac{{ \cos }^{2}x+2{ \sin }^{2}x}{ \sin x \cos x}=\dfrac{1+2{ \tan }^{2}x}{ \tan x} $ ,故 $ \mathrm{B} $ 正确;
对于 $ \mathrm{C} $ , $ \sin ({53}^{\circ }-x)= \sin [{90}^{\circ }-({37}^{\circ }+x)]= \cos ({37}^{\circ }+x) $ ,故 $ \mathrm{C} $ 正确;
对于 $ \mathrm{D} $ , $ \cos ({480}^{\circ }+x)= \cos ({120}^{\circ }+x)= \cos [{180}^{\circ }-({60}^{\circ }-x)]=- \cos ({60}^{\circ }-x) $ ,故 $ \mathrm{D} $ 错误.故选 $ \mathrm{A}\mathrm{B}\mathrm{C} $ .
12. $ \dfrac{ \cos (-{585}^{\circ })}{ \tan {585}^{\circ }+ \sin {570}^{\circ }}= $ ( )
A. $ \dfrac{\sqrt{2}}{3} $
B. $ -\dfrac{\sqrt{2}}{3} $
C. $ \sqrt{2} $
D. $ -\sqrt{2} $
答案:D
解析:由题意 $ \dfrac{ \cos (-{585}^{\circ })}{ \tan {585}^{\circ }+ \sin {570}^{\circ }} $
$ =\dfrac{ \cos ({135}^{\circ }-{360}^{\circ }×2)}{ \tan ({45}^{\circ }+{180}^{\circ }×3)+ \sin ({210}^{\circ }+{360}^{\circ })} $
$ =\dfrac{ \cos {135}^{\circ }}{ \tan {45}^{\circ }+ \sin {210}^{\circ }} $
$ =\dfrac{ \cos ({45}^{\circ }+{90}^{\circ })}{ \tan {45}^{\circ }+ \sin ({30}^{\circ }+{180}^{\circ })} $
$ =\dfrac{- \sin {45}^{\circ }}{ \tan {45}^{\circ }- \sin {30}^{\circ }} $
$ =\dfrac{-\dfrac{\sqrt{2}}{2}}{1-\dfrac{1}{2}}=-\sqrt{2} $ ,故选 $ \mathrm{D} $ .
二、刷能力
1.若角 $ \alpha $ 的终边过点 $ (3,1) $ ,则 $ \sin (\alpha +\dfrac{\mathrm{\pi }}{2})= $ ( )
A. $ \dfrac{3\sqrt{10}}{10} $
B. $ -\dfrac{3\sqrt{10}}{10} $
C. $ \dfrac{\sqrt{10}}{10} $
D. $ -\dfrac{\sqrt{10}}{10} $
答案:A
解析:角 $ \alpha $ 的终边过点 $ (3,1) $ ,则点 $ (3,1) $ 到原点的距离 $ r=\sqrt{{3}^{2}+{1}^{2}}=\sqrt{10} $ ,
所以 $ \cos \alpha =\dfrac{3}{r}=\dfrac{3}{\sqrt{10}}=\dfrac{3\sqrt{10}}{10} $ ,
所以 $ \sin (\alpha +\dfrac{\mathrm{\pi }}{2})= \cos \alpha =\dfrac{3\sqrt{10}}{10} $ .故选 $ \mathrm{A} $ .
2.已知 $ \sin (\alpha +\dfrac{\mathrm{\pi }}{6})=\dfrac{2}{5} $ , $ \alpha \in (0,\mathrm{\pi }) $ ,则 $ \sin (\alpha -\dfrac{\mathrm{\pi }}{3})= $ ( )
A. $ -\dfrac{\sqrt{21}}{5} $
B. $ \dfrac{\sqrt{21}}{5} $
C. $ -\dfrac{2}{5} $
D. $ \dfrac{2}{5} $
答案:B
解析: $ \sin (\alpha +\dfrac{\mathrm{\pi }}{6})= \sin (\alpha -\dfrac{\mathrm{\pi }}{3}+\dfrac{\mathrm{\pi }}{2})= \cos (\alpha -\dfrac{\mathrm{\pi }}{3})=\dfrac{2}{5}\in (0,\dfrac{1}{2}) $ ,
而 $ \alpha \in (0,\mathrm{\pi }) $ ,则 $ \alpha -\dfrac{\mathrm{\pi }}{3}\in (-\dfrac{\mathrm{\pi }}{3} $ , $ \dfrac{2\mathrm{\pi }}{3}) $ ,
所以 $ \alpha -\dfrac{\mathrm{\pi }}{3}\in (\dfrac{\mathrm{\pi }}{3},\dfrac{\mathrm{\pi }}{2}) $ ,
所以 $ \sin (\alpha -\dfrac{\mathrm{\pi }}{3})=\dfrac{\sqrt{21}}{5} $ .故选 $ \mathrm{B} $ .
3.已知角 $ A $ , $ B $ , $ C $ 为 $ △ABC $ 的三个内角,若 $ \sin \dfrac{A+B-C}{2}= \sin \dfrac{A-B+C}{2} $ ,则 $ △ABC $ 一定是( )
A.等腰直角三角形
B.直角三角形
C.等腰三角形
D.钝角三角形
答案:C
解析:因为 $ \sin \dfrac{A+B-C}{2}= \sin \dfrac{A-B+C}{2} $ ,
$ A+B+C=\mathrm{\pi } $ ,
所以 $ \sin \dfrac{\mathrm{\pi }-2C}{2}= \sin \dfrac{\mathrm{\pi }-2B}{2} $ ,
可得 $ \cos C= \cos B $ .
又因为 $ B $ , $ C\in (0,\mathrm{\pi }) $ ,
所以 $ B=C $ ,则 $ AC=AB $ ,所以 $ △ABC $ 一定是等腰三角形.故选 $ \mathrm{C} $ .
4.已知 $ f(x)=\begin{cases} \sin \mathrm{\pi }x,x < 0,\\ f(x-1)-1,x > 0,\end{cases} $ 则 $ f(-\dfrac{11}{6})+f(\dfrac{11}{6}) $ 的值为( )
A.2
B.1
C. $ -2 $
D. $ -1 $
答案:C
解析:因为 $ f(x)=\begin{cases} \sin \mathrm{\pi }x,x < 0,\\ f(x-1)-1,x > 0,\end{cases} $
所以 $ f(-\dfrac{11}{6})= \sin (-\dfrac{11\mathrm{\pi }}{6}) $
$ = \sin (-\dfrac{11\mathrm{\pi }}{6}+2\mathrm{\pi })= \sin \dfrac{\mathrm{\pi }}{6}=\dfrac{1}{2} $ ,
$ f(\dfrac{11}{6})=f(\dfrac{11}{6}-1)-1=f(\dfrac{5}{6})-1 $
$ =f(\dfrac{5}{6}-1)-1-1=f(-\dfrac{1}{6})-2 $
$ = \sin (-\dfrac{\mathrm{\pi }}{6})-2=- \sin \dfrac{\mathrm{\pi }}{6}-2 $
$ =-\dfrac{1}{2}-2 $ ,
故 $ f(-\dfrac{11}{6})+f(\dfrac{11}{6})=\dfrac{1}{2}-\dfrac{1}{2}-2=-2 $ .
故选 $ \mathrm{C} $ .
5.若 $ a= \cos \dfrac{11\mathrm{\pi }}{6} $ , $ b= \sin \dfrac{\mathrm{\pi }}{6} $ , $ c= \tan \dfrac{100\mathrm{\pi }}{3} $ ,则 $ a $ , $ b $ , $ c $ 的大小关系为( )
A. $ a < b < c $
B. $ b < a < c $
C. $ c < a < b $
D. $ b < c < a $
答案:B
解析:由于 $ \cos \dfrac{11\mathrm{\pi }}{6}= \cos (2\mathrm{\pi }-\dfrac{\mathrm{\pi }}{6})= \cos \dfrac{\mathrm{\pi }}{6}=\dfrac{\sqrt{3}}{2} $ ,故 $ a=\dfrac{\sqrt{3}}{2} $ .
而 $ \dfrac{\sqrt{3}}{2} > \dfrac{1}{2}= \sin \dfrac{\mathrm{\pi }}{6}=b $ ,故 $ a > b $ .
又 $ c= \tan \dfrac{100\mathrm{\pi }}{3}= \tan (33\mathrm{\pi }+\dfrac{\mathrm{\pi }}{3})= \tan \dfrac{\mathrm{\pi }}{3}=\sqrt{3} $ ,所以 $ c > a > b $ ,故选 $ \mathrm{B} $ .
6.化简: $ \dfrac{ \sin (\mathrm{\pi }+\alpha ) \cos (3\mathrm{\pi }+\alpha ) \cos (\dfrac{\mathrm{\pi }}{2}+\alpha )}{ \sin (\dfrac{5\mathrm{\pi }}{2}-\alpha ) \sin (-\mathrm{\pi }-\alpha )}= $ .
解析:易知
$ \dfrac{ \sin (\mathrm{\pi }+\alpha ) \cos (3\mathrm{\pi }+\alpha ) \cos (\dfrac{\mathrm{\pi }}{2}+\alpha )}{ \sin (\dfrac{5\mathrm{\pi }}{2}-\alpha ) \sin (-\mathrm{\pi }-\alpha )}=\dfrac{- \sin \alpha \cos (2\mathrm{\pi }+\mathrm{\pi }+\alpha ) \cos (\dfrac{\mathrm{\pi }}{2}+\alpha )}{ \sin (2\mathrm{\pi }+\dfrac{\mathrm{\pi }}{2}-\alpha ) \sin (2\mathrm{\pi }-\mathrm{\pi }-\alpha )} $
$ =\dfrac{- \sin \alpha \cos (\mathrm{\pi }+\alpha ) \cos (\dfrac{\mathrm{\pi }}{2}+\alpha )}{ \sin (\dfrac{\mathrm{\pi }}{2}-\alpha ) \sin (\mathrm{\pi }-\alpha )} $
$ =\dfrac{- \sin \alpha (- \cos \alpha )(- \sin \alpha )}{ \cos \alpha \sin \alpha }=- \sin \alpha $ .
7.已知 $ f(n)= \sin (\dfrac{n\mathrm{\pi }}{2}+\dfrac{\mathrm{\pi }}{4})(n\in {\boldsymbol{N}}^{\ast }) $ ,则 $ f(1)+f(2)+f(3)+\cdots +f(2023)= $ .
答案: $ -\dfrac{\sqrt{2}}{2} $
解析:取 $ n=1 {\rm ,2,3,4} $ 可得 $ f(1)+f(2)+f(3)+f(4)=\dfrac{\sqrt{2}}{2}-\dfrac{\sqrt{2}}{2}-\dfrac{\sqrt{2}}{2}+\dfrac{\sqrt{2}}{2}=0 $ ,
从而可得 $ f(4k+1)+f(4k+2)+f(4k+3)+f(4k+4)=\dfrac{\sqrt{2}}{2}-\dfrac{\sqrt{2}}{2}-\dfrac{\sqrt{2}}{2}+\dfrac{\sqrt{2}}{2}=0 $ , $ k\in \boldsymbol{N} $ ,
则 $ f(1)+f(2)+f(3)+\cdots +f(2023) $
$ =505×[f(1)+f(2)+f(3)+f(4)]+f(2021)+f(2022)+f(2023) $
$ =f(1)+f(2)+f(3)=\dfrac{\sqrt{2}}{2}-\dfrac{\sqrt{2}}{2}-\dfrac{\sqrt{2}}{2}=-\dfrac{\sqrt{2}}{2} $ .
8.如图,在平面直角坐标系中,锐角 $ \alpha $ 的终边与单位圆交于点 $ P(\dfrac{\sqrt{5}}{5},m) $ ,将角 $ \alpha $ 的终边按逆时针方向旋转 $ \dfrac{\mathrm{\pi }}{2} $ 后得到角 $ \beta $ 的终边,并与单位圆交于点 $ Q $ .
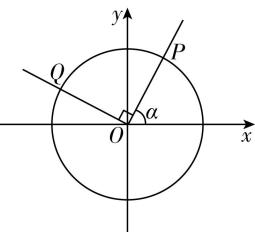
(1) 求点 $ Q $ 的坐标;
(2) 求 $ \dfrac{ \sin (\dfrac{\mathrm{\pi }}{2}-\alpha ) \cos (\mathrm{\pi }-\beta )}{\sqrt{5} \cos (2025\mathrm{\pi }+\beta )+2 \tan (\mathrm{\pi }-\beta )} $ 的值.
答案:【解】(1) 由 $ P(\dfrac{\sqrt{5}}{5},m) $ ,得 $ \cos \alpha =\dfrac{\sqrt{5}}{5} $ ,
又 $ \alpha \in (0,\dfrac{\mathrm{\pi }}{2}) $ ,
所以 $ \sin \alpha =\sqrt{1-{ \cos }^{2}\alpha }=\dfrac{2\sqrt{5}}{5} $ .
由题可知 $ \beta =\dfrac{\mathrm{\pi }}{2}+\alpha $ ,
所以 $ \sin \beta = \sin (\alpha +\dfrac{\mathrm{\pi }}{2})= \cos \alpha =\dfrac{\sqrt{5}}{5} $ ,
$ \cos \beta = \cos (\alpha +\dfrac{\mathrm{\pi }}{2})=- \sin \alpha =-\dfrac{2\sqrt{5}}{5} $ ,
所以点 $ Q $ 的坐标为 $ (-\dfrac{2\sqrt{5}}{5} $ , $ \dfrac{\sqrt{5}}{5}) $ .
(2) 由(1)可知 $ \tan \beta =\dfrac{ \sin \beta }{ \cos \beta }=\dfrac{\dfrac{\sqrt{5}}{5}}{-\dfrac{2\sqrt{5}}{5}}=-\dfrac{1}{2} $ .
所以 $ \dfrac{ \sin (\dfrac{\mathrm{\pi }}{2}-\alpha ) \cos (\mathrm{\pi }-\beta )}{\sqrt{5} \cos (2025\mathrm{\pi }+\beta )+2 \tan (\mathrm{\pi }-\beta )} $
$ =\dfrac{ \cos \alpha (- \cos \beta )}{\sqrt{5}(- \cos \beta )+2(- \tan \beta )} $
$ =\dfrac{\dfrac{\sqrt{5}}{5}×\dfrac{2\sqrt{5}}{5}}{\sqrt{5}×\dfrac{2\sqrt{5}}{5}+2×\dfrac{1}{2}}=\dfrac{\dfrac{2}{5}}{2+1}=\dfrac{2}{15} $ .
解析:
9. $ n $ 为整数,化简 $ \dfrac{ \sin (n\mathrm{\pi }+\alpha )}{ \cos (n\mathrm{\pi }+\alpha )} $ 的结果是( )
A. $ ± \tan \alpha $
B. $ - \tan \alpha $
C. $ \tan \alpha $
D. $ \tan n\alpha $
答案:C
解析:当 $ n=2k(k\in \boldsymbol{Z}) $ 时,原式 $ =\dfrac{ \sin (2k\mathrm{\pi }+\alpha )}{ \cos (2k\mathrm{\pi }+\alpha )}=\dfrac{ \sin \alpha }{ \cos \alpha }= \tan \alpha $ .
当 $ n=2k+1(k\in \boldsymbol{Z}) $ 时,原式 $ =\dfrac{ \sin (2k\mathrm{\pi }+\mathrm{\pi }+\alpha )}{ \cos (2k\mathrm{\pi }+\mathrm{\pi }+\alpha )}=\dfrac{ \sin (\mathrm{\pi }+\alpha )}{ \cos (\mathrm{\pi }+\alpha )}=\dfrac{- \sin \alpha }{- \cos \alpha }= \tan \alpha $ .
综上,原式 $ = \tan \alpha $ .故选 $ \mathrm{C} $ .
10.k为整数,化简 $ \dfrac{ \sin [(k+1)\mathrm{\pi }+\theta ]· \cos [(k+1)\mathrm{\pi }-\theta ]}{ \sin (k\mathrm{\pi }-\theta )· \cos (k\mathrm{\pi }+\theta )} $ 的结果是 ( )
A.±1
B.−1
C.1
D.tan $ {\rm \mathit{θ}} $
答案:B
解析:当k为偶数时,设k=2n,n∈Z,
则原式 $ {\rm =} \dfrac{ \sin [(2n+1)\mathrm{\pi }+\theta ] \cos [(2n+1)\mathrm{\pi }-\theta ]}{ \sin (2n\mathrm{\pi }-\theta ) \cos (2n\mathrm{\pi }+\theta )} $
$ {\rm =} \dfrac{ \sin (\mathrm{\pi }+\theta )· \cos (\mathrm{\pi }-\theta )}{- \sin \theta · \cos \theta } $
$ {\rm =} \dfrac{- \sin \theta ·(- \cos \theta )}{- \sin \theta · \cos \theta } $
=−1.
当k为奇数时,设k=2n+1,n∈Z,
则原式 $ {\rm =} \dfrac{ \sin [(2n+2)\mathrm{\pi }+\theta ] \cos [(2n+2)\mathrm{\pi }-\theta ]}{ \sin [(2n+1)\mathrm{\pi }-\theta ] \cos [(2n+1)\mathrm{\pi }+\theta ]} $
$ {\rm =} \dfrac{ \sin [2(n+1)\mathrm{\pi }+\theta ] \cos [2(n+1)\mathrm{\pi }-\theta ]}{ \sin (\mathrm{\pi }-\theta ) \cos (\mathrm{\pi }+\theta )} $
$ {\rm =} \dfrac{ \sin \theta · \cos \theta }{ \sin \theta ·(- \cos \theta )} $
=−1.
综上,原式的值为−1.故选B.
11.已知 $ \cos (\dfrac{\mathrm{\pi }}{6}-\theta )=a(|a|\leqslant 1) $ ,则 $ \cos (\dfrac{5\mathrm{\pi }}{6}+\theta )+ \sin (\dfrac{2\mathrm{\pi }}{3}-\theta ) $ 的值是 .
解析: $ \because \cos (\dfrac{5\mathrm{\pi }}{6}+\theta )= \cos [\mathrm{\pi }-(\dfrac{\mathrm{\pi }}{6}-\theta )]=- \cos (\dfrac{\mathrm{\pi }}{6}-\theta )=-a $ ,
$ \sin (\dfrac{2\mathrm{\pi }}{3}-\theta )= \sin [\dfrac{\mathrm{\pi }}{2}+(\dfrac{\mathrm{\pi }}{6}-\theta )] $
$ = \cos (\dfrac{\mathrm{\pi }}{6}-\theta )=a $ ,
$ \therefore \cos (\dfrac{5\mathrm{\pi }}{6}+\theta )+ \sin (\dfrac{2\mathrm{\pi }}{3}-\theta )=0 $ .
12.已知cos(508 $ {\rm \mathit{°}} $ - $ {\rm \mathit{α}} $ )= $ \dfrac{12}{13} $ ,则cos(212 $ {\rm \mathit{°}} $ + $ {\rm \mathit{α}} $ )= .
解析:因为 $ {\rm cos(508\mathit{°}-\mathit{α})=cos(360\mathit{°}+148\mathit{°}-\mathit{α})=cos(148\mathit{°}-\mathit{α})=} \dfrac{12}{13} $ ,所以 $ {\rm cos(212\mathit{°}+\mathit{α})=cos(360\mathit{°}+\mathit{α}-148\mathit{°})=cos(\mathit{α}-148\mathit{°})=cos(148\mathit{°}-\mathit{α})=} \dfrac{12}{13} {\rm \mathit{.}} $
