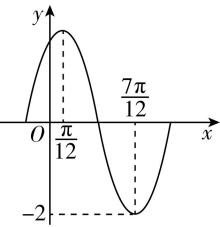
9.(多选)已知函数 $ f(x)=A \sin (\omega x+\varphi )(A > 0,\omega > 0,0 < \varphi < \mathrm{\pi }) $ 的部分图象如图所示,则下列结论正确的是( )
 (多选)
(多选)
A.函数 $ f(x) $ 的最小正周期为 $ \mathrm{\pi } $
B.直线 $ x=\dfrac{\mathrm{\pi }}{3} $ 是 $ f(x) $ 图象的一条对称轴
C.点 $ (\dfrac{5\mathrm{\pi }}{6},0) $ 是 $ f(x) $ 图象的一个对称中心
D.点 $ (-\dfrac{\mathrm{\pi }}{3},0) $ 是 $ f(x) $ 图象的一个对称中心
设 $ f(x)=A \sin (\omega x+\varphi )(A > 0,\omega > 0,0 < \varphi < \mathrm{\pi }) $ 的最小正周期为 $ T $ ,
由题中图象可知 $ \dfrac{7\mathrm{\pi }}{12}-\dfrac{\mathrm{\pi }}{12}=\dfrac{1}{2}T $ ,解得 $ T=\mathrm{\pi } $ ,故 $ \mathrm{A} $ 正确.
因为 $ \omega > 0 $ ,所以 $ \omega =\dfrac{2\mathrm{\pi }}{T} $ ,解得 $ \omega =2 $ .由题图可知 $ A=2 $ ,故 $ f(x)=2 \sin (2x+\varphi ) $ .
将点 $ (\dfrac{7\mathrm{\pi }}{12},-2) $ 的坐标代入解析式化简得 $ \sin (\dfrac{\mathrm{\pi }}{6}+\varphi )=1 $ ,因为 $ 0 < \varphi < \mathrm{\pi } $ ,所以 $ \dfrac{\mathrm{\pi }}{6}+\varphi =\dfrac{\mathrm{\pi }}{2} $ ,解得 $ \varphi =\dfrac{\mathrm{\pi }}{3} $ ,故 $ f(x)=2 \sin (2x+\dfrac{\mathrm{\pi }}{3}) $ .
当 $ x=\dfrac{\mathrm{\pi }}{3} $ 时, $ 2x+\dfrac{\mathrm{\pi }}{3}=\mathrm{\pi } $ ,则点 $ (\dfrac{\mathrm{\pi }}{3},0) $ 是函数 $ f(x) $ 图象的对称中心,则直线 $ x=\dfrac{\mathrm{\pi }}{3} $ 不是 $ f(x) $ 图象的对称轴,故 $ \mathrm{B} $ 错误.
当 $ x=\dfrac{5\mathrm{\pi }}{6} $ 时, $ 2x+\dfrac{\mathrm{\pi }}{3}=2\mathrm{\pi } $ ,则点 $ (\dfrac{5\mathrm{\pi }}{6},0) $ 是函数 $ f(x) $ 图象的对称中心,故 $ \mathrm{C} $ 正确.
当 $ x=-\dfrac{\mathrm{\pi }}{3} $ 时, $ 2x+\dfrac{\mathrm{\pi }}{3}=-\dfrac{\mathrm{\pi }}{3} $ ,则点 $ (-\dfrac{\mathrm{\pi }}{3},0) $ 不是函数 $ f(x) $ 图象的对称中心,故 $ \mathrm{D} $ 错误.故选 $ \mathrm{A}\mathrm{C} $ .