5.4.3 正切函数的性质与图象
一、刷基础
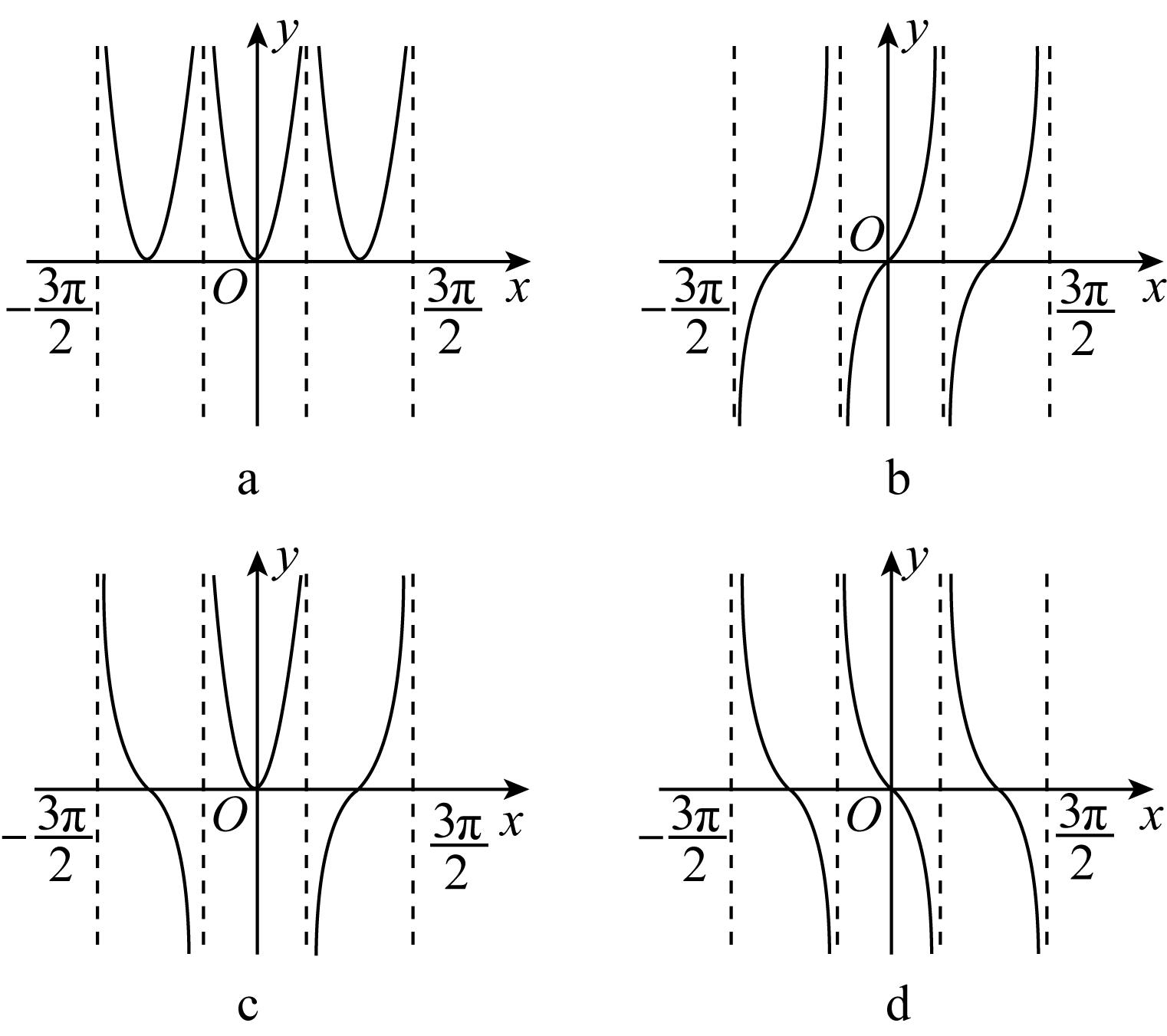
1.下列图形分别是 $ \mathrm{①}y=\left| \tan \text{ }x\right| $ ; $ \mathrm{②}y= \tan \text{ }x $ ; $ \mathrm{③}y= \tan (-x) $ ; $ \mathrm{④}y= \tan \left|x\right| $ 在 $ x\in (-\dfrac{3\mathrm{\pi }}{2},\dfrac{3\mathrm{\pi }}{2}) $ 内的大致图象,那么由 $ \mathrm{a} $ 到 $ \mathrm{d} $ 对应的函数关系式应是( )
A.①②③④
B.①③④②
C.③②④①
D.①②④③
答案:D
解析: $ y= \tan (-x)=- \tan \text{ }x $ 在 $ (-\dfrac{\mathrm{\pi }}{2},\dfrac{\mathrm{\pi }}{2}) $ 上是单调递减的,只有图象 $ \mathrm{d} $ 符合,即 $ \mathrm{d} $ 对应③.故选 $ \mathrm{D} $ .
2.函数 $ y= \tan (\dfrac{1}{2}x-\dfrac{\mathrm{\pi }}{3}) $ 在一个周期内的图象是( )
A.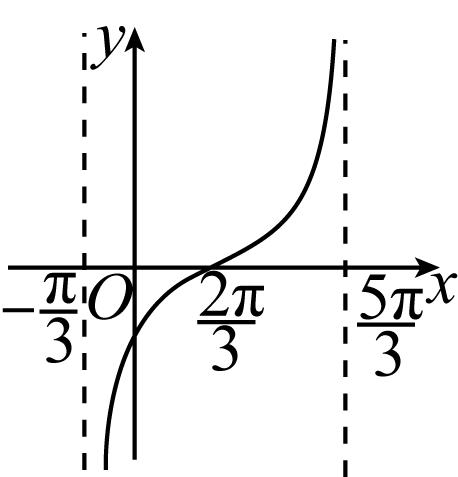
B.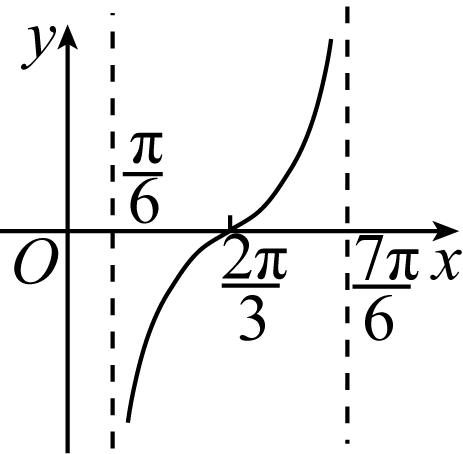
C.
D.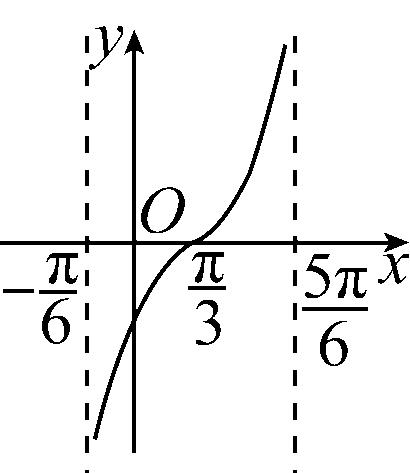
答案:A
解析:当 $ x=\dfrac{2\mathrm{\pi }}{3} $ 时, $ y=0 $ ,排除 $ \mathrm{C} $ , $ \mathrm{D} $ ;当 $ x=0 $ 时, $ y= \tan (-\dfrac{\mathrm{\pi }}{3})=-\sqrt{3} $ ,排除 $ \mathrm{B} $ .故选 $ \mathrm{A} $ .
3.函数 $ f(x)=a-\sqrt{3} \tan \text{ }2x $ 在 $ x\in [-\dfrac{\mathrm{\pi }}{6},b] $ 的最大值为7,最小值为3,则 $ ab $ 为( )
A. $ \dfrac{5\mathrm{\pi }}{12} $
B. $ \dfrac{\mathrm{\pi }}{3} $
C. $ \dfrac{\mathrm{\pi }}{6} $
D. $ \dfrac{\mathrm{\pi }}{12} $
答案:B
解析: $ \because x\in [-\dfrac{\mathrm{\pi }}{6},b] $ , $ \therefore b > -\dfrac{\mathrm{\pi }}{6} $ , $ \therefore 2x\in [-\dfrac{\mathrm{\pi }}{3},2b] $ ,
又 $ \because $ 函数 $ f(x) $ 在 $ x\in [-\dfrac{\mathrm{\pi }}{6},b] $ 的最大值为7,最小值为 $ {\rm 3,} \therefore 2b < \dfrac{\mathrm{\pi }}{2} $ ,即 $ b < \dfrac{\mathrm{\pi }}{4} $ .
根据正切函数 $ g(x)= \tan \text{ }x $ 在 $ (-\dfrac{\mathrm{\pi }}{2},\dfrac{\mathrm{\pi }}{2}) $ 上单调递增,则 $ f(x)=a-\sqrt{3} \tan \text{ }2x $ 在 $ [-\dfrac{\mathrm{\pi }}{6},b] $ 上单调递减,
$ \therefore f(-\dfrac{\mathrm{\pi }}{6})=a+3=7⇒a=4 $ , $ \therefore f(b)=4-\sqrt{3} \tan \text{ }2b=3 $ ,则 $ \tan \text{ }2b=\dfrac{\sqrt{3}}{3} $ ,
$ \because 2b\in (-\dfrac{\mathrm{\pi }}{3},\dfrac{\mathrm{\pi }}{2}) $ , $ \therefore 2b=\dfrac{\mathrm{\pi }}{6} $ , $ \therefore b=\dfrac{\mathrm{\pi }}{12} $ , $ \therefore ab=4×\dfrac{\mathrm{\pi }}{12}=\dfrac{\mathrm{\pi }}{3} $ ,故选 $ \mathrm{B} $ .
4. $ y= \lg ( \tan x-1) $ 的定义域为 .
答案: $ {x|\dfrac{\mathrm{\pi }}{4}+k\mathrm{\pi } < x < \dfrac{\mathrm{\pi }}{2}+k\mathrm{\pi },k\in \boldsymbol{Z}} $
解析:令 $ y= \lg t $ , $ t= \tan x-1 $ ,
函数 $ t= \tan x-1 $ 的定义域为 $ {x|x\ne \dfrac{\mathrm{\pi }}{2}+k\mathrm{\pi },k\in \boldsymbol{Z}} $ ,
函数 $ y= \lg t $ 的定义域为 $ {t|t > 0} $ ,则 $ \tan x-1 > 0 $ ,即 $ \dfrac{\mathrm{\pi }}{4}+k\mathrm{\pi } < x < \dfrac{\mathrm{\pi }}{2}+k\mathrm{\pi } $ , $ k\in \boldsymbol{Z} $ ,
所以 $ y= \lg ( \tan x-1) $ 的定义域为 $ {x|\dfrac{\mathrm{\pi }}{4}+k\mathrm{\pi } < x < \dfrac{\mathrm{\pi }}{2}+k\mathrm{\pi },k\in \boldsymbol{Z}} $ .
5.函数 $ f(x)= \tan (\omega x-\dfrac{\mathrm{\pi }}{4}) $ 与函数 $ g(x)= \sin (\dfrac{\mathrm{\pi }}{4}-2x) $ 的最小正周期相同,则 $ \omega = $ ( )
A. $ ±1 $
B.1
C. $ ±2 $
D.2
答案:A
解析:因为函数 $ f(x)= \tan (x-\dfrac{\mathrm{\pi }}{4}) $ 与函数 $ g(x)= \sin (\dfrac{\mathrm{\pi }}{4}-2x) $ 的最小正周期相同,所以 $ \dfrac{\mathrm{\pi }}{\left|\omega \right|}=\dfrac{2\mathrm{\pi }}{2} $ ,所以 $ \omega =±1 $ ,故选 $ \mathrm{A} $ .
6.(多选)已知函数 $ f(x)= \tan (\omega x-\dfrac{\omega }{2}\mathrm{\pi })(\omega > 0) $ 的最小正周期为 $ 2\mathrm{\pi } $ ,则( )(多选)
A. $ \omega =1 $
B. $ y=f(x) $ 的图象的对称中心为 $ (2k\mathrm{\pi }+\mathrm{\pi },0)(k\in \boldsymbol{Z}) $
C. $ f(x) $ 在 $ (-\dfrac{\mathrm{\pi }}{2},\dfrac{\mathrm{\pi }}{2}) $ 上单调递增
D. $ f(x+\dfrac{\mathrm{\pi }}{2}) $ 是奇函数
答案:CD
解析: $ \mathrm{A} $ : $ T=\dfrac{\mathrm{\pi }}{\omega }=2\mathrm{\pi }⇒\omega =\dfrac{1}{2} $ ,故 $ \mathrm{A} $ 错误;
$ \mathrm{B} $ :令 $ \dfrac{x}{2}-\dfrac{\mathrm{\pi }}{4}=\dfrac{\mathrm{\pi }}{2}k $ , $ k\in \boldsymbol{Z} $ ,则 $ x=\dfrac{\mathrm{\pi }}{2}+k\mathrm{\pi } $ , $ k\in \boldsymbol{Z} $ ,所以 $ f(x) $ 图象的对称中心为 $ (k\mathrm{\pi }+\dfrac{\mathrm{\pi }}{2},0)(k\in \boldsymbol{Z}) $ ,故 $ \mathrm{B} $ 错误;
$ \mathrm{C} $ :由选项 $ \mathrm{A} $ 知 $ f(x)= \tan (\dfrac{x}{2}-\dfrac{\mathrm{\pi }}{4}) $ ,
当 $ x\in (-\dfrac{\mathrm{\pi }}{2},\dfrac{\mathrm{\pi }}{2}) $ 时, $ \dfrac{x}{2}-\dfrac{\mathrm{\pi }}{4}\in (-\dfrac{\mathrm{\pi }}{2},0) $ , $ f(x) $ 在 $ (-\dfrac{\mathrm{\pi }}{2},\dfrac{\mathrm{\pi }}{2}) $ 上单调递增,故 $ \mathrm{C} $ 正确;
$ \mathrm{D} $ :设函数 $ g(x)=f(x+\dfrac{\mathrm{\pi }}{2})= \tan \dfrac{x}{2} $ ,则 $ g(-x)=-g(x) $ ,显然 $ g(x) $ 的定义域关于原点对称,故 $ f(x+\dfrac{\mathrm{\pi }}{2}) $ 是奇函数,故 $ \mathrm{D} $ 正确.故选 $ \mathrm{C}\mathrm{D} $ .
7.函数 $ f(x)=\dfrac{1}{2} \tan (3x-\dfrac{\mathrm{\pi }}{5})+2025 $ 图象的对称中心为 .
答案: $ (\dfrac{k\mathrm{\pi }}{6}+\dfrac{\mathrm{\pi }}{15},2025)(k\in \boldsymbol{Z}) $
解析:令 $ 3x-\dfrac{\mathrm{\pi }}{5}=\dfrac{k\mathrm{\pi }}{2} $ , $ k\in \boldsymbol{Z} $ ,解得 $ x=\dfrac{k\mathrm{\pi }}{6}+\dfrac{\mathrm{\pi }}{15} $ , $ k\in \boldsymbol{Z} $ ,
所以函数 $ f(x)=\dfrac{1}{2} \tan (3x-\dfrac{\mathrm{\pi }}{5})+2025 $ 图象的对称中心为 $ (\dfrac{k\mathrm{\pi }}{6}+\dfrac{\mathrm{\pi }}{15},2025)(k\in \boldsymbol{Z}) $ .
8.(多选)下列不等关系成立的是( )(多选)
A. $ \tan 1 > \sin 1 > \cos 1 $
B. $ \sin 2 > \cos 2 > \tan 2 $
C. $ \tan 3 > \sin 3 > \cos 3 $
D. $ \tan 4 > \cos 4 > \sin 4 $
答案:ABD
解析:对于 $ \mathrm{A} $ , $ \dfrac{\mathrm{\pi }}{4} < 1 < \dfrac{\mathrm{\pi }}{2} $ ,故 $ \tan 1 > \tan \dfrac{\mathrm{\pi }}{4}=1 $ , $ \sin 1 > \sin \dfrac{\mathrm{\pi }}{4}= \cos \dfrac{\mathrm{\pi }}{4} > \cos 1 $ ,故 $ \tan 1 > \sin 1 > \cos 1 $ , $ \mathrm{A} $ 正确;
对于 $ \mathrm{B} $ , $ \dfrac{\mathrm{\pi }}{2} < 2 < \dfrac{2\mathrm{\pi }}{3} $ ,则 $ \sin 2 > 0 $ , $ 0 > \cos 2 > \cos \dfrac{2\mathrm{\pi }}{3}=-\dfrac{1}{2} $ , $ -\sqrt{3}= \tan \dfrac{2\mathrm{\pi }}{3} > \tan 2 $ ,
则 $ \sin 2 > \cos 2 > \tan 2 $ , $ \mathrm{B} $ 正确;
对于 $ \mathrm{C} $ , $ \dfrac{5\mathrm{\pi }}{6} < 3 < \mathrm{\pi } $ ,故 $ \sin 3 > 0 $ , $ -1 < \cos 3 < \cos \dfrac{5\mathrm{\pi }}{6}=-\dfrac{\sqrt{3}}{2} $ , $ 0 > \tan 3 > \tan \dfrac{5\mathrm{\pi }}{6}=-\dfrac{\sqrt{3}}{3} $ ,
故 $ \sin 3 > \tan 3 > \cos 3 $ , $ \mathrm{C} $ 错误;
对于 $ \mathrm{D} $ , $ \dfrac{5\mathrm{\pi }}{4} < 4 < \dfrac{4\mathrm{\pi }}{3} $ ,则 $ \tan 4 > 0 $ , $ \cos 4 > \cos \dfrac{5\mathrm{\pi }}{4}=-\dfrac{\sqrt{2}}{2} $ , $ \sin 4 < \sin \dfrac{5\mathrm{\pi }}{4}=-\dfrac{\sqrt{2}}{2} $ ,
故 $ \tan 4 > \cos 4 > \sin 4 $ , $ \mathrm{D} $ 正确.故选 $ \mathrm{A}\mathrm{B}\mathrm{D} $ .
9.若函数 $ f(x)=1- \tan (\omega x-\dfrac{\mathrm{\pi }}{4})(\omega \ne 0) $ 在 $ (0,1) $ 上单调递增,则 $ \omega $ 的取值范围是( )
A. $ [-\dfrac{\mathrm{\pi }}{2},0) $
B. $ (-\dfrac{\mathrm{\pi }}{2},-\dfrac{\mathrm{\pi }}{4}] $
C. $ (0,\dfrac{\mathrm{\pi }}{4}] $
D. $ [-\dfrac{\mathrm{\pi }}{4},0) $
答案:D
解析:函数 $ f(x)=1+ \tan (-\omega x+\dfrac{\mathrm{\pi }}{4}) $ 在 $ (0,1) $ 上单调递增,
根据正切函数的性质,可得 $ -\omega > 0 $ ,
当 $ x\in (0,1) $ 时, $ -\omega x+\dfrac{\mathrm{\pi }}{4}\in (\dfrac{\mathrm{\pi }}{4} $ , $ -\omega +\dfrac{\mathrm{\pi }}{4}) $ ,则 $ -\omega +\dfrac{\mathrm{\pi }}{4}\leqslant \dfrac{\mathrm{\pi }}{2} $ ,解得 $ -\dfrac{\mathrm{\pi }}{4}\leqslant \omega < 0 $ .故选 $ \mathrm{D} $ .
10.不等式 $ -1\leqslant \tan (\dfrac{1}{2}x+\dfrac{\mathrm{\pi }}{6})\leqslant \sqrt{3} $ 的解集是 .
答案: $ [-\dfrac{5\mathrm{\pi }}{6}+2k\mathrm{\pi },\dfrac{\mathrm{\pi }}{3}+2k\mathrm{\pi }] $ , $ k\in \boldsymbol{Z} $
解析:因为 $ y= \tan \text{ }x $ 在 $ (-\dfrac{\mathrm{\pi }}{2}+k\mathrm{\pi },\dfrac{\mathrm{\pi }}{2}+k\mathrm{\pi }) $ , $ k\in \boldsymbol{Z} $ 上单调递增,
所以由 $ -1\leqslant \tan (\dfrac{1}{2}x+\dfrac{\mathrm{\pi }}{6})\leqslant \sqrt{3} $ 得 $ -\dfrac{\mathrm{\pi }}{4}+k\mathrm{\pi }\leqslant \dfrac{1}{2}x+\dfrac{\mathrm{\pi }}{6}\leqslant \dfrac{\mathrm{\pi }}{3}+k\mathrm{\pi } $ , $ k\in \boldsymbol{Z} $ ,
解得 $ -\dfrac{5\mathrm{\pi }}{6}+2k\mathrm{\pi }\leqslant x\leqslant \dfrac{\mathrm{\pi }}{3}+2k\mathrm{\pi } $ , $ k\in \boldsymbol{Z} $ ,
即不等式 $ -1\leqslant \tan (\dfrac{1}{2}x+\dfrac{\mathrm{\pi }}{6})\leqslant \sqrt{3} $ 的解集是 $ [-\dfrac{5\mathrm{\pi }}{6}+2k\mathrm{\pi },\dfrac{\mathrm{\pi }}{3}+2k\mathrm{\pi }] $ , $ k\in \boldsymbol{Z} $ .
二、刷提升
1.已知 $ x\in (-\dfrac{\mathrm{\pi }}{2},\dfrac{\mathrm{\pi }}{4}] $ ,则函数 $ f(x)={(\dfrac{1}{3})}^{ \tan x} $ 的值域是( )
A. $ (0,\dfrac{1}{3}] $
B. $ (0,3] $
C. $ [\dfrac{1}{3},+\mathrm{\infty }) $
D. $ [3,+\mathrm{\infty }) $
答案:C
解析:令 $ t= \tan x $ ,则 $ f(x)={(\dfrac{1}{3})}^{ \tan x}={\left(\dfrac{1}{3}\right) ^ {t}} $ ,
因为 $ t= \tan x $ 在 $ (-\dfrac{\mathrm{\pi }}{2},\dfrac{\mathrm{\pi }}{4}] $ 上单调递增,且 $ \tan \dfrac{\mathrm{\pi }}{4}=1 $ ,所以 $ t= \tan x\in (-\mathrm{\infty },1] $ .
又 $ y={\left(\dfrac{1}{3}\right) ^ {t}} $ 单调递减,
所以 $ y={\left(\dfrac{1}{3}\right) ^ {t}}\in [\dfrac{1}{3},+\mathrm{\infty }) $ ,即 $ f(x) $ 的值域是 $ [\dfrac{1}{3},+\mathrm{\infty }) $ .故选 $ \mathrm{C} $ .
2.下列函数中最小正周期为 $ \mathrm{\pi } $ 且是奇函数的为( )
A. $ y= \tan 2x $
B. $ y= \tan (x+\dfrac{\mathrm{\pi }}{4}) $
C. $ y= \cos (2x+\dfrac{3}{2}\mathrm{\pi }) $
D. $ y= \sin (2x+\dfrac{\mathrm{\pi }}{2}) $
答案:C
解析:对于 $ \mathrm{A} $ , $ y= \tan 2x $ 的最小正周期 $ T=\dfrac{\mathrm{\pi }}{2} $ ,故 $ \mathrm{A} $ 不符合;
对于 $ \mathrm{B} $ , $ y= \tan (x+\dfrac{\mathrm{\pi }}{4}) $ 为非奇非偶函数,故 $ \mathrm{B} $ 不符合;
对于 $ \mathrm{C} $ , $ y= \cos (2x+\dfrac{3}{2}\mathrm{\pi })= \sin 2x $ 为奇函数,且最小正周期 $ T=\dfrac{2\mathrm{\pi }}{2}=\mathrm{\pi } $ ,故 $ \mathrm{C} $ 符合;
对于 $ \mathrm{D} $ , $ y= \sin (2x+\dfrac{\mathrm{\pi }}{2})= \cos 2x $ 为偶函数,故 $ \mathrm{D} $ 不符合.故选 $ \mathrm{C} $ .
3.已知定义在 $ (-\dfrac{\mathrm{\pi }}{2},\dfrac{\mathrm{\pi }}{2}) $ 上的函数 $ f(x)={x}^{3}+ \tan x+2 $ ,则不等式 $ f(x-2)+f(\dfrac{x}{2}) > 4 $ 的解集是( )
A. $ (\dfrac{4}{3},+\mathrm{\infty }) $
B. $ (2-\dfrac{\mathrm{\pi }}{2},\mathrm{\pi }) $
C. $ (\dfrac{4}{3},\mathrm{\pi }) $
D. $ (\dfrac{4}{3},\dfrac{\mathrm{\pi }}{2}+2) $
答案:C
解析:令 $ F(x)=f(x)-2={x}^{3}+ \tan x $ ,则函数 $ F(x) $ 的定义域 $ (-\dfrac{\mathrm{\pi }}{2},\dfrac{\mathrm{\pi }}{2}) $ 关于原点对称,
且 $ F(-x)=f(-x)-2={\left(-x\right) ^ {3}}+ \tan (-x)=-({x}^{3}+ \tan x)=-F(x) $ ,
所以函数 $ F(x) $ 是奇函数,所以不等式 $ f(x-2)+f(\dfrac{x}{2}) > 4⇔f(x-2)-2 > -[f(\dfrac{x}{2})-2]⇔F(x-2) > -F(\dfrac{x}{2})⇔F(x-2) > F(-\dfrac{x}{2}) $ .
因为函数 $ y={x}^{3} $ 和 $ y= \tan x $ 在 $ (-\dfrac{\mathrm{\pi }}{2},\dfrac{\mathrm{\pi }}{2}) $ 上均单调递增,
所以函数 $ F(x) $ 为定义在 $ (-\dfrac{\mathrm{\pi }}{2},\dfrac{\mathrm{\pi }}{2}) $ 上的增函数,
所以 $ \begin{cases}-\dfrac{\mathrm{\pi }}{2} < x-2 < \dfrac{\mathrm{\pi }}{2},\\ -\dfrac{\mathrm{\pi }}{2} < -\dfrac{x}{2} < \dfrac{\mathrm{\pi }}{2},\\ x-2 > -\dfrac{x}{2},\end{cases} $ 解得 $ \dfrac{4}{3} < x < \mathrm{\pi } $ ,所以不等式 $ f(x-2)+f(\dfrac{x}{2}) > 4 $ 的解集是 $ (\dfrac{4}{3},\mathrm{\pi }) $ .故选 $ \mathrm{C} $ .
4.已知函数 $ f(x)= \tan x+| \tan x| $ ,则下列结论中正确的有( )
A. $ f(x) $ 的最小正周期为 $ \dfrac{\mathrm{\pi }}{2} $
B. $ f(x) $ 的值域为 $ (-\mathrm{\infty },+\mathrm{\infty }) $
C.点 $ (\dfrac{3\mathrm{\pi }}{2},0) $ 是 $ f(x) $ 图象的一个对称中心
D.不等式 $ f(x) > 2\sqrt{3} $ 的解集为 $ (\dfrac{\mathrm{\pi }}{3}+k\mathrm{\pi } $ , $ \dfrac{\mathrm{\pi }}{2}+k\mathrm{\pi } ) (k\in \boldsymbol{Z} ) $
答案:D
解析: $ f\left(x\right)= \tan x+\mid \tan x\mid =\begin{cases}2 \tan x,x\in \left[k\mathrm{\pi },\dfrac{\mathrm{\pi }}{2}+k\mathrm{\pi }\right),k\in \boldsymbol{Z},\\ 0,x\in \left(-\dfrac{\mathrm{\pi }}{2}+k\mathrm{\pi },k\mathrm{\pi }\right),k\in \boldsymbol{Z},\end{cases} $
作出 $ f(x) $ 的图象如图所示.
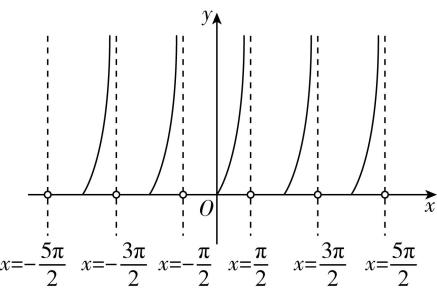
对于 $ \mathrm{A} $ , $ f(x) $ 的最小正周期为 $ \mathrm{\pi } $ , $ \mathrm{A} $ 错误;
对于 $ \mathrm{B} $ , $ f(x) $ 的值域为 $ [0,+\mathrm{\infty }) $ , $ \mathrm{B} $ 错误;
对于 $ \mathrm{C} $ , $ f(x) $ 的图象没有对称中心, $ \mathrm{C} $ 错误;
对于 $ \mathrm{D} $ ,不等式 $ f(x) > 2\sqrt{3} $ ,即 $ x\in [k\mathrm{\pi },\dfrac{\mathrm{\pi }}{2}+k\mathrm{\pi })(k\in \boldsymbol{Z}) $ 时, $ 2 \tan x > 2\sqrt{3} $ ,得 $ \tan x > \sqrt{3} $ ,解得 $ \dfrac{\mathrm{\pi }}{3}+k\mathrm{\pi } < x < \dfrac{\mathrm{\pi }}{2}+k\mathrm{\pi } $ , $ k\in \boldsymbol{Z} $ ,所以 $ f(x) > 2\sqrt{3} $ 的解集为 $ (\dfrac{\mathrm{\pi }}{3}+k\mathrm{\pi } $ , $ \dfrac{\mathrm{\pi }}{2}+k\mathrm{\pi } ) (k\in \boldsymbol{Z} ) $ , $ \mathrm{D} $ 正确.故选 $ \mathrm{D} $ .
5.已知函数 $ f(x)= \tan (x+\theta ) $ , $ \theta \in (0,\dfrac{\mathrm{\pi }}{2}) $ .甲:当 $ x\in (0,\dfrac{\mathrm{\pi }}{4}) $ 时,函数 $ f(x) $ 单调递减;乙:函数 $ f(x) $ 的图象关于直线 $ x=\dfrac{\mathrm{\pi }}{3} $ 对称;丙:函数 $ f(x) $ 图象的一个对称中心为 $ (\dfrac{\mathrm{\pi }}{6},0) $ .甲、乙、丙三人对函数 $ f(x) $ 的论述中有且只有一个正确,则 $ \theta = $ .
答案: $ \dfrac{\mathrm{\pi }}{3} $
解析:由于 $ f(x)= \tan (x+\theta ) $ , $ \theta \in (0,\dfrac{\mathrm{\pi }}{2}) $ ,故 $ f(x) $ 的图象没有对称轴,因此乙的论述是错误的,
易知函数 $ f(x) $ 不能在 $ x\in (0,\dfrac{\mathrm{\pi }}{4}) $ 时单调递减,故甲的论述错误,则丙的论述是正确的,即函数 $ f(x) $ 的图象关于 $ (\dfrac{\mathrm{\pi }}{6},0) $ 对称,则 $ \dfrac{\mathrm{\pi }}{6}+\theta =\dfrac{1}{2}k\mathrm{\pi } $ , $ k\in \boldsymbol{Z} $ ,故 $ \theta =-\dfrac{\mathrm{\pi }}{6}+\dfrac{1}{2}k\mathrm{\pi } $ , $ k\in \boldsymbol{Z} $ ,结合 $ \theta \in (0,\dfrac{\mathrm{\pi }}{2}) $ ,得 $ \theta =\dfrac{\mathrm{\pi }}{3} $ .
6.函数 $ f (x )= \tan (\omega x+\varphi ) (\omega > 0 $ , $ |\varphi | < \dfrac{\mathrm{\pi }}{2}) $ 的图象如图所示,图中阴影部分的面积为 $ 6\mathrm{\pi } $ ,则函数 $ y=f(x) $ 的解析式为 .
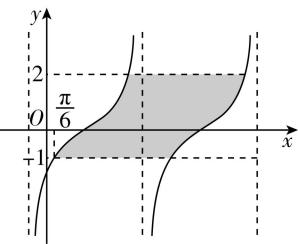
答案: $ f(x)= \tan (\dfrac{1}{2}x-\dfrac{\mathrm{\pi }}{3}) $
解析:如图所示,区域①和区域③面积相等,故阴影部分的面积即为矩形 $ ABCD $ 的面积,
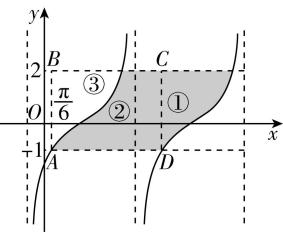
可得 $ |AB|=3 $ ,设函数 $ f(x) $ 的最小正周期为 $ T $ ,则 $ |AD|=T $ ,
由题意可得 $ 3T=6\mathrm{\pi } $ ,解得 $ T=2\mathrm{\pi } $ ,故 $ \dfrac{\mathrm{\pi }}{\omega }=2\mathrm{\pi } $ ,可得 $ \omega =\dfrac{1}{2} $ ,即 $ f(x)= \tan (\dfrac{1}{2}x+\varphi ) $ .
又 $ f(x) $ 的图象过点 $ (\dfrac{\mathrm{\pi }}{6},-1) $ ,
即 $ \tan (\dfrac{1}{2}×\dfrac{\mathrm{\pi }}{6}+\varphi )= \tan (\dfrac{\mathrm{\pi }}{12}+\varphi )=-1 $ .
因为 $ \varphi \in (-\dfrac{\mathrm{\pi }}{2},\dfrac{\mathrm{\pi }}{2}) $ ,所以 $ \dfrac{\mathrm{\pi }}{12}+\varphi =-\dfrac{\mathrm{\pi }}{4} $ ,解得 $ \varphi =-\dfrac{\mathrm{\pi }}{3} $ ,故 $ f(x)= \tan (\dfrac{1}{2}x-\dfrac{\mathrm{\pi }}{3}) $ .
7.函数 $ f(x)= \tan (\omega x+\varphi )(\omega > 0,0 < \varphi < \dfrac{\mathrm{\pi }}{2}) $ ,已知函数 $ y=f(x) $ 的图象与 $ x $ 轴相邻两个交点间的距离为 $ \mathrm{\pi } $ ,且图象关于点 $ M(-\dfrac{\mathrm{\pi }}{16},0) $ 对称.
(1) 求 $ f(x) $ 的单调区间;
(2) 求不等式 $ -1\leqslant f(x)\leqslant \sqrt{3} $ 的解集.
答案:(1) 【解】由题意知,函数 $ f(x) $ 的最小正周期为 $ T=\dfrac{\mathrm{\pi }}{|\omega |}=\mathrm{\pi } $ .
因为 $ \omega > 0 $ ,所以 $ \omega =1 $ ,
所以 $ f(x)= \tan (x+\varphi ) $ .
因为函数 $ y=f(x) $ 的图象关于点 $ M(-\dfrac{\mathrm{\pi }}{16},0) $ 对称,
所以 $ -\dfrac{\mathrm{\pi }}{16}+\varphi =\dfrac{k\mathrm{\pi }}{2} $ , $ k\in \boldsymbol{Z} $ ,即 $ \varphi =\dfrac{k\mathrm{\pi }}{2}+\dfrac{\mathrm{\pi }}{16} $ , $ k\in \boldsymbol{Z} $ .
因为 $ 0 < \varphi < \dfrac{\mathrm{\pi }}{2} $ ,所以 $ \varphi =\dfrac{\mathrm{\pi }}{16} $ ,故 $ f(x)= \tan (x+\dfrac{\mathrm{\pi }}{16}) $ .
令 $ -\dfrac{\mathrm{\pi }}{2}+k\mathrm{\pi } < x+\dfrac{\mathrm{\pi }}{16} < \dfrac{\mathrm{\pi }}{2}+k\mathrm{\pi } $ , $ k\in \boldsymbol{Z} $ ,得 $ -\dfrac{9\mathrm{\pi }}{16}+k\mathrm{\pi } < x < \dfrac{7\mathrm{\pi }}{16}+k\mathrm{\pi } $ , $ k\in \boldsymbol{Z} $ ,
所以函数的单调递增区间为 $ (-\dfrac{9\mathrm{\pi }}{16}+k\mathrm{\pi },\dfrac{7\mathrm{\pi }}{16}+k\mathrm{\pi }) $ , $ k\in \boldsymbol{Z} $ ,无单调递减区间.
(2) 【解】由(1)知, $ f(x)= \tan (x+\dfrac{\mathrm{\pi }}{16}) $ .
由 $ -1\leqslant \tan (x+\dfrac{\mathrm{\pi }}{16})\leqslant \sqrt{3} $ ,
得 $ -\dfrac{\mathrm{\pi }}{4}+k\mathrm{\pi }\leqslant x+\dfrac{\mathrm{\pi }}{16}\leqslant \dfrac{\mathrm{\pi }}{3}+k\mathrm{\pi } $ , $ k\in \boldsymbol{Z} $ ,
即 $ -\dfrac{5\mathrm{\pi }}{16}+k\mathrm{\pi }\leqslant x\leqslant \dfrac{13\mathrm{\pi }}{48}+k\mathrm{\pi } $ , $ k\in \boldsymbol{Z} $ ,
所以不等式 $ -1\leqslant f(x)\leqslant \sqrt{3} $ 的解集为 $ {x|-\dfrac{5\mathrm{\pi }}{16}+k\mathrm{\pi }\leqslant x\leqslant \dfrac{13\mathrm{\pi }}{48}+k\mathrm{\pi },k\in \boldsymbol{Z}} $ .
解析:
8. $ f(x)= \tan x \sin x- \sin x- \tan x+1 $ 在 $ [0,2\mathrm{\pi }] $ 上的零点个数为( )
A.1
B.2
C.3
D.4
答案:B
解析:依题意, $ f(x)= \tan x \sin x- \sin x- \tan x+1=( \tan x-1)( \sin x-1) $ ,而 $ x\in [0,2\mathrm{\pi }] $ ,显然 $ x\ne \dfrac{\mathrm{\pi }}{2} $ 且 $ x\ne \dfrac{3\mathrm{\pi }}{2} $ ,因此 $ \sin x\ne 1 $ ,
由 $ f(x)=0 $ ,得 $ \tan x=1 $ ,解得 $ x=\dfrac{\mathrm{\pi }}{4} $ 或 $ x=\dfrac{5}{4}\mathrm{\pi } $ ,
所以 $ f(x) $ 在 $ [0,2\mathrm{\pi }] $ 上的零点个数是2.故选 $ \mathrm{B} $ .