第5.4节综合训练
一、刷能力
1.在 $ [0,2\mathrm{\pi }] $ 上函数 $ f(x)=\sqrt{1-2 \cos x}+ \ln ( \sin x-\dfrac{\sqrt{2}}{2}) $ 的定义域是( )
A. $ [\dfrac{\mathrm{\pi }}{4},\dfrac{\mathrm{\pi }}{3}] $
B. $ [\dfrac{3\mathrm{\pi }}{4},\dfrac{5\mathrm{\pi }}{3}] $
C. $ [\dfrac{\mathrm{\pi }}{3},\dfrac{3\mathrm{\pi }}{4}) $
D. $ [\dfrac{\mathrm{\pi }}{3},\dfrac{3\mathrm{\pi }}{4}] $
答案:C
解析:由函数 $ f(x)=\sqrt{1-2 \cos x}+ \ln ( \sin x-\dfrac{\sqrt{2}}{2}) $ ,可知 $ \begin{cases}1-2 \cos x\geqslant 0,\\ \sin x-\dfrac{\sqrt{2}}{2} > 0,\end{cases} $ 其中 $ x\in [0,2\mathrm{\pi }] $ ,即 $ \begin{cases} \cos x\leqslant \dfrac{1}{2},\\ \sin x > \dfrac{\sqrt{2}}{2},\end{cases} $ 其中 $ x\in [0,2\mathrm{\pi }] $ ,解得 $ \dfrac{\mathrm{\pi }}{3}\leqslant x < \dfrac{3\mathrm{\pi }}{4} $ ,即函数 $ f(x) $ 的定义域为 $ [\dfrac{\mathrm{\pi }}{3},\dfrac{3\mathrm{\pi }}{4}) $ .故选 $ \mathrm{C} $ .
2.若函数 $ f(x)= \sin (\omega x+\dfrac{\mathrm{\pi }}{3})(\omega > 0) $ 在 $ [0,\dfrac{\mathrm{\pi }}{6}] $ 上单调递增,则 $ \omega $ 的取值范围是( )
A. $ (0,2] $
B. $ (0,1] $
C. $ (0,\dfrac{1}{2}] $
D. $ [\dfrac{1}{2},1] $
答案:B
解析:由题设 $ t=\omega x+\dfrac{\mathrm{\pi }}{3}\in [\dfrac{\mathrm{\pi }}{3} $ , $ \dfrac{\mathrm{\pi }}{6}\omega +\dfrac{\mathrm{\pi }}{3} ] $ ,则 $ y= \sin t $ 在 $ [\dfrac{\mathrm{\pi }}{3} $ , $ \dfrac{\mathrm{\pi }}{6}\omega +\dfrac{\mathrm{\pi }}{3} ] $ 上单调递增,所以 $ \dfrac{\mathrm{\pi }}{6}\omega +\dfrac{\mathrm{\pi }}{3}\leqslant \dfrac{\mathrm{\pi }}{2} $ ,解得 $ \omega \leqslant 1 $ ,又 $ \omega > 0 $ ,所以 $ 0 < \omega \leqslant 1 $ .故选 $ \mathrm{B} $ .
3.已知 $ a= \cos \dfrac{9\mathrm{\pi }}{5} $ , $ b= \sin \dfrac{20\mathrm{\pi }}{7} $ , $ c= \tan \dfrac{19\mathrm{\pi }}{3} $ ,则有( )
A. $ a > b > c $
B. $ a > c > b $
C. $ c > a > b $
D. $ c > b > a $
答案:C
解析: $ a= \cos \dfrac{9\mathrm{\pi }}{5}= \cos (\dfrac{9\mathrm{\pi }}{5}-2\mathrm{\pi })= \cos (-\dfrac{\mathrm{\pi }}{5})= \cos \dfrac{\mathrm{\pi }}{5}= \sin \dfrac{3\mathrm{\pi }}{10} $ ,
$ b= \sin \dfrac{20\mathrm{\pi }}{7}= \sin (2\mathrm{\pi }+\dfrac{6\mathrm{\pi }}{7})= \sin \dfrac{6\mathrm{\pi }}{7}= \sin \dfrac{\mathrm{\pi }}{7} $ ,因为 $ y= \sin x $ 在 $ (0,\dfrac{\mathrm{\pi }}{2}) $ 上单调递
增,所以 $ \sin \dfrac{\mathrm{\pi }}{7} < \sin \dfrac{3\mathrm{\pi }}{10} $ ,又 $ c= \tan \dfrac{19\mathrm{\pi }}{3}= \tan (6\mathrm{\pi }+\dfrac{\mathrm{\pi }}{3})= \tan \dfrac{\mathrm{\pi }}{3}=\sqrt{3} $ ,所以 $ b < a < 1 < c $ .故选 $ \mathrm{C} $ .
4.函数 $ f(x)=\dfrac{ \sin x}{{\mathrm{e}}^{x}+{\mathrm{e}}^{-x}} \cos x $ 的图象大致是( )
A.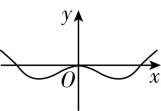
B.
C.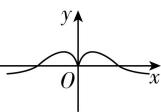
D.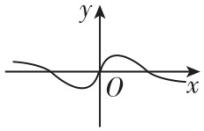
答案:D
解析:函数 $ f(x)=\dfrac{ \sin x}{{\mathrm{e}}^{x}+{\mathrm{e}}^{-x}} \cos x $ 的定义域为 $ \boldsymbol{R} $ ,由 $ f(-x)=\dfrac{ \sin (-x) \cos (-x)}{{\mathrm{e}}^{-x}+{\mathrm{e}}^{x}}=\dfrac{- \sin x \cos x}{{\mathrm{e}}^{x}+{\mathrm{e}}^{-x}}=-f(x) $ ,可得函数 $ f(x) $ 是 $ \boldsymbol{R} $ 上的奇函数,图象关于原点对称,排除 $ \mathrm{A} $ , $ \mathrm{C} $ ;
当 $ x\in [0,\dfrac{\mathrm{\pi }}{2}] $ 时, $ f(x)\geqslant 0 $ ,且当 $ x=0 $ 或 $ x=\dfrac{\mathrm{\pi }}{2} $ 时取等号,排除 $ \mathrm{B} $ .故选 $ \mathrm{D} $ .
5.已知函数 $ f(x)= \cos (\omega x+\varphi )(\omega > 0,\left|\varphi \right| < \dfrac{\mathrm{\pi }}{2}) $ 的最小正周期为 $ \mathrm{\pi } $ ,且当 $ x=\dfrac{\mathrm{\pi }}{3} $ 时,函数 $ f(x) $ 取最小值,若函数 $ f(x) $ 在 $ [a,0] $ 上单调递减,则 $ a $ 的最小值是( )
A. $ -\dfrac{\mathrm{\pi }}{6} $
B. $ -\dfrac{5\mathrm{\pi }}{6} $
C. $ -\dfrac{2\mathrm{\pi }}{3} $
D. $ -\dfrac{\mathrm{\pi }}{3} $
答案:A
解析:因为 $ \omega > 0 $ ,所以 $ \omega =\dfrac{2\mathrm{\pi }}{T}=\dfrac{2\mathrm{\pi }}{\mathrm{\pi }}=2 $ ,故 $ \cos (2×\dfrac{\mathrm{\pi }}{3}+\varphi )=-1 $ ,所以 $ \dfrac{2\mathrm{\pi }}{3}+\varphi =\mathrm{\pi }+2k\mathrm{\pi } $ , $ k\in \boldsymbol{Z} $ ,解得 $ \varphi =\dfrac{\mathrm{\pi }}{3}+2k\mathrm{\pi } $ , $ k\in \boldsymbol{Z} $ .
因为 $ \left|\varphi \right| < \dfrac{\mathrm{\pi }}{2} $ ,所以只有当 $ k=0 $ 时, $ \varphi =\dfrac{\mathrm{\pi }}{3} $ 满足要求,故 $ f(x)= \cos (2x+\dfrac{\mathrm{\pi }}{3}) $ .
因为 $ x\in [a,0] $ ,所以 $ 2x+\dfrac{\mathrm{\pi }}{3}\in [2a+\dfrac{\mathrm{\pi }}{3},\dfrac{\mathrm{\pi }}{3}] $ ,故 $ 2a+\dfrac{\mathrm{\pi }}{3}\in [0,\dfrac{\mathrm{\pi }}{3}) $ ,解得 $ a\in [-\dfrac{\mathrm{\pi }}{6},0) $ ,故 $ a $ 的最小值为 $ -\dfrac{\mathrm{\pi }}{6} $ .故选 $ \mathrm{A} $ .
6.函数 $ f(x)= \sin x $ ,若方程 $ f(x)-4[f(x)]^{2}=a $ 在 $ (\dfrac{\mathrm{\pi }}{6},\mathrm{\pi }) $ 内有两个不同的解,则实数 $ a $ 的取值范围为( )
A. $ (-1,0)\cup (0,\dfrac{1}{16}) $
B. $ (-1,-\dfrac{1}{2})\cup (\dfrac{1}{2},\dfrac{1}{16}) $
C. $ (-3,-1)\cup (0,\dfrac{1}{4}) $
D. $ (-3,-\dfrac{1}{2})\cup (0,\dfrac{1}{16}) $
答案:D
解析:当 $ x\in (\dfrac{\mathrm{\pi }}{6},\mathrm{\pi }) $ 时, $ f(x)= \sin x $ 的图象如图所示,
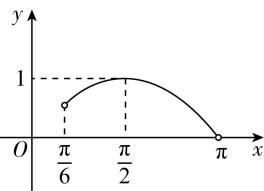
则 $ f(x)= \sin x\in (0,1] $ ,令 $ f(x)=t $ ,则方程为 $ t-4{t}^{2}=a $ , $ t\in (0,1] $ .
又 $ f(\dfrac{\mathrm{\pi }}{6})= \sin \dfrac{\mathrm{\pi }}{6}=\dfrac{1}{2} $ ,当 $ t\in (\dfrac{1}{2},1) $ 时,若方程 $ f(x)-4[f(x)]^{2}=a $ 在 $ (\dfrac{\mathrm{\pi }}{6},\mathrm{\pi }) $ 内有两个不同的解,
只需 $ t-4{t}^{2}=a $ 只有一解,即直线 $ y=a $ 与函数 $ y=-4{t}^{2}+t $ , $ t\in (\dfrac{1}{2},1) $ 的图象只有一个交点,
又函数 $ y=-4{t}^{2}+t $ 在 $ (\dfrac{1}{2},1) $ 上单调递减,所以 $ -4×{1}^{2}+1 < a < -4×{\left(\dfrac{1}{2}\right) ^ {2}}+\dfrac{1}{2} $ ,即 $ a\in (-3,-\dfrac{1}{2}) $ ;
当 $ t=1 $ 时, $ a=-4+1=-3 $ ,方程 $ 4[f(x)]^{2}-f(x)-3=0 $ 的解为 $ f(x)=1 $ 和 $ f(x)=-\dfrac{3}{4} $ ,
当 $ f(x)=1 $ 时, $ x=\dfrac{\mathrm{\pi }}{2} $ ,当 $ f(x)=-\dfrac{3}{4} $ 时,无解,即方程 $ f(x)-4[f(x)]^{2}=a $ 在 $ (\dfrac{\mathrm{\pi }}{6},\mathrm{\pi }) $ 内只有一解,不合题意;
当 $ t=\dfrac{1}{2} $ 时, $ a=-1+\dfrac{1}{2}=-\dfrac{1}{2} $ ,方程 $ 4[f(x)]^{2}-f(x)-\dfrac{1}{2}=0 $ 的解为 $ f(x)=\dfrac{1}{2} $ 和 $ f(x)=-\dfrac{1}{4} $ ,
当 $ f(x)=\dfrac{1}{2} $ 时, $ x=\dfrac{5\mathrm{\pi }}{6} $ ,当 $ f(x)=-\dfrac{1}{4} $ 时,无解,即方程 $ f(x)-4[f(x)]^{2}=a $ 在 $ (\dfrac{\mathrm{\pi }}{6},\mathrm{\pi }) $ 内只有一解,不合题意;
当 $ t\in (0,\dfrac{1}{2}) $ 时,若方程 $ 4[f(x)]^{2}-f(x)+a=0 $ 在 $ (\dfrac{\mathrm{\pi }}{6},\mathrm{\pi }) $ 内有两个不同的解,
只需 $ 4{t}^{2}-t+a=0 $ 有两个不同的解,
即直线 $ y=a $ 与函数 $ y=-4{t}^{2}+t $ , $ t\in (0,\dfrac{1}{2}) $ 的图象有两个交点,
又函数 $ y=-4{t}^{2}+t $ 在 $ (0,\dfrac{1}{8}) $ 上单调递增,在 $ (\dfrac{1}{8},\dfrac{1}{2}) $ 上单调递减,
所以 $ -4×{0}^{2}+0 < a < -4×{\left(\dfrac{1}{8}\right) ^ {2}}+\dfrac{1}{8} $ ,所以 $ a\in (0,\dfrac{1}{16}) $ .
综上所述,实数 $ a $ 的取值范围为 $ (-3,-\dfrac{1}{2})\cup (0,\dfrac{1}{16}) $ .故选 $ \mathrm{D} $ .
7.(多选)已知函数 $ f(x)= \tan (-x+\dfrac{\mathrm{\pi }}{3}) $ ,则下列说法正确的是( )(多选)
A. $ f(x) $ 的定义域是 $ {x|x\ne k\mathrm{\pi }-\dfrac{\mathrm{\pi }}{6},k\in \boldsymbol{Z}} $
B. $ f(x) $ 的最小正周期为 $ 2\mathrm{\pi } $
C. $ f(x) $ 在区间 $ (k\mathrm{\pi }-\dfrac{\mathrm{\pi }}{6} $ , $ k\mathrm{\pi }+\dfrac{5\mathrm{\pi }}{6} ) (k\in \boldsymbol{Z} ) $ 上单调递减
D. $ f(x) $ 图象的对称中心为 $ (k\mathrm{\pi }+\dfrac{\mathrm{\pi }}{3},0)(k\in \boldsymbol{Z}) $
答案:AC
解析:自变量 $ x $ 的取值应满足 $ -x+\dfrac{\mathrm{\pi }}{3}\ne k\mathrm{\pi }+\dfrac{\mathrm{\pi }}{2} $ , $ k\in \boldsymbol{Z} $ ,解得 $ x\ne -k\mathrm{\pi }-\dfrac{\mathrm{\pi }}{6} $ , $ k\in \boldsymbol{Z} $ ,所以 $ f(x) $ 的定义域是 $ {x|x\ne k\mathrm{\pi }-\dfrac{\mathrm{\pi }}{6} $ , $ k\in \boldsymbol{Z}} $ ,故 $ \mathrm{A} $ 正确;
$ f(x) $ 的最小正周期为 $ \dfrac{\mathrm{\pi }}{|-1|}=\mathrm{\pi } $ ,故 $ \mathrm{B} $ 错误;
由 $ k\mathrm{\pi }-\dfrac{\mathrm{\pi }}{2} < -x+\dfrac{\mathrm{\pi }}{3} < k\mathrm{\pi }+\dfrac{\mathrm{\pi }}{2} $ , $ k\in \boldsymbol{Z} $ ,解得 $ -k\mathrm{\pi }-\dfrac{\mathrm{\pi }}{6} < x < -k\mathrm{\pi }+\dfrac{5\mathrm{\pi }}{6} $ , $ k\in \boldsymbol{Z} $ ,
所以 $ f(x) $ 在区间 $ (k\mathrm{\pi }-\dfrac{\mathrm{\pi }}{6},k\mathrm{\pi }+\dfrac{5\mathrm{\pi }}{6})(k\in \boldsymbol{Z}) $ 上单调递减,故 $ \mathrm{C} $ 正确;
由 $ -x+\dfrac{\mathrm{\pi }}{3}=\dfrac{k\mathrm{\pi }}{2} $ , $ k\in \boldsymbol{Z} $ ,解得 $ x=-\dfrac{k\mathrm{\pi }}{2}+\dfrac{\mathrm{\pi }}{3} $ , $ k\in \boldsymbol{Z} $ ,所以 $ f(x) $ 图象的对称中心为 $ (\dfrac{k\mathrm{\pi }}{2}+\dfrac{\mathrm{\pi }}{3},0)(k\in \boldsymbol{Z}) $ ,故 $ \mathrm{D} $ 错误.故选 $ \mathrm{A}\mathrm{C} $ .
8.(多选)设函数 $ f(x)= \sin (\omega x-\dfrac{\mathrm{\pi }}{6})(\omega > 0) $ ,则下列说法正确的是( )(多选)
A.若 $ f(x) $ 的最小正周期为 $ \mathrm{\pi } $ ,则 $ \omega =2 $
B.若 $ \omega =1 $ ,则 $ f(x) $ 的图象关于点 $ (\dfrac{2\mathrm{\pi }}{3},0) $ 对称
C.若 $ f(x) $ 在区间 $ [0,\dfrac{\mathrm{\pi }}{2}] $ 上单调递增,则 $ 0 < \omega < \dfrac{4}{3} $
D.若 $ f(x) $ 在区间 $ [0,2\mathrm{\pi }] $ 上恰有2个零点,则 $ \dfrac{7}{12}\leqslant \omega < \dfrac{13}{12} $
答案:AD
解析:对于 $ \mathrm{A} $ ,若 $ f(x) $ 的最小正周期为 $ \mathrm{\pi } $ ,则 $ \dfrac{2\mathrm{\pi }}{\omega }=\mathrm{\pi } $ ,解得 $ \omega =2 $ ,故 $ \mathrm{A} $ 正确;
对于 $ \mathrm{B} $ ,若 $ \omega =1 $ ,则 $ f(x)= \sin (x-\dfrac{\mathrm{\pi }}{6}) $ ,
当 $ x=\dfrac{2\mathrm{\pi }}{3} $ 时, $ f(x)= \sin (\dfrac{2\mathrm{\pi }}{3}-\dfrac{\mathrm{\pi }}{6})=1 $ ,故 $ \mathrm{B} $ 错误;
对于 $ \mathrm{C} $ ,当 $ x\in [0 $ , $ \dfrac{\mathrm{\pi }}{2} ] $ 时, $ \omega x-\dfrac{\mathrm{\pi }}{6}\in [-\dfrac{\mathrm{\pi }}{6} $ , $ \dfrac{\mathrm{\pi }\omega }{2}-\dfrac{\mathrm{\pi }}{6} ] $ ,
因为 $ f(x) $ 在 $ [0 $ , $ \dfrac{\mathrm{\pi }}{2} ] $ 上单调递增,所以 $ -\dfrac{\mathrm{\pi }}{6} < \dfrac{\mathrm{\pi }\omega }{2}-\dfrac{\mathrm{\pi }}{6}\leqslant \dfrac{\mathrm{\pi }}{2} $ ,解得 $ 0 < \omega \leqslant \dfrac{4}{3} $ ,故 $ \mathrm{C} $ 错误;
对于 $ \mathrm{D} $ ,当 $ x\in [0,2\mathrm{\pi }] $ 时, $ \omega x-\dfrac{\mathrm{\pi }}{6}\in [-\dfrac{\mathrm{\pi }}{6} $ , $ 2\mathrm{\pi }\omega -\dfrac{\mathrm{\pi }}{6} ] $ ,
若 $ f(x) $ 在 $ [0,2\mathrm{\pi }] $ 上恰有2个零点,
则 $ \mathrm{\pi }\leqslant 2\mathrm{\pi }\omega -\dfrac{\mathrm{\pi }}{6} < 2\mathrm{\pi } $ ,解得 $ \dfrac{7}{12}\leqslant \omega < \dfrac{13}{12} $ ,故 $ \mathrm{D} $ 正确.故选 $ \mathrm{A}\mathrm{D} $ .
9.(多选)已知函数 $ f(x)= \sin (\omega x+\varphi )(0 < \omega < 3,|\varphi | < \dfrac{\mathrm{\pi }}{2}) $ 图象和直线y $ =\dfrac{\sqrt{2}}{2} $ 相邻两交点 $ A({x}_{1},\dfrac{\sqrt{2}}{2}) $ , $ B({x}_{2},\dfrac{\sqrt{2}}{2}) $ ,若 $ |{x}_{1}-{x}_{2}|=\dfrac{\mathrm{\pi }}{3} $ ,且函数 $ y=f(x-\dfrac{\mathrm{\pi }}{6}) $ 为奇函数,则( )(多选)
A. $ \omega =2 $
B. $ \varphi =\dfrac{\mathrm{\pi }}{4} $
C.函数 $ f(x+\dfrac{\mathrm{\pi }}{6}) $ 为偶函数
D.函数 $ f(x) $ 在区间 $ (0,\dfrac{\mathrm{\pi }}{3}) $ 上单调递增
答案:BC
解析:因为 $ y= \sin x $ 和 $ y=\dfrac{\sqrt{2}}{2} $ 图象的相邻交点间的距离是 $ \dfrac{\mathrm{\pi }}{2} $ 或 $ \dfrac{3\mathrm{\pi }}{2} $ ,
且 $ A({x}_{1},\dfrac{\sqrt{2}}{2}) $ , $ B({x}_{2},\dfrac{\sqrt{2}}{2}) $ 为相邻两交点,
所以 $ |(\omega {x}_{1}+\varphi )-(\omega {x}_{2}+\varphi )|=\dfrac{\mathrm{\pi }}{2} $ 或 $ \dfrac{3\mathrm{\pi }}{2} $ ,
所以 $ \omega |{x}_{1}-{x}_{2}|=\dfrac{\mathrm{\pi }}{2} $ 或 $ \dfrac{3\mathrm{\pi }}{2} $ ,又 $ |{x}_{1}-{x}_{2}|=\dfrac{\mathrm{\pi }}{3} $ ,
所以 $ \omega =\dfrac{3}{2} $ 或 $ \omega =\dfrac{9}{2} $ ,又 $ 0 < \omega < 3 $ ,所以 $ \omega =\dfrac{3}{2} $ , $ \mathrm{A} $ 错误;
因为 $ y=f(x-\dfrac{\mathrm{\pi }}{6})= \sin [\dfrac{3}{2}(x-\dfrac{\mathrm{\pi }}{6})+\varphi ]= \sin (\dfrac{3}{2}x-\dfrac{\mathrm{\pi }}{4}+\varphi ) $ 为奇函数,
所以 $ -\dfrac{\mathrm{\pi }}{4}+\varphi =k\mathrm{\pi } $ , $ k\in \boldsymbol{Z} $ ,即 $ \varphi =k\mathrm{\pi }+\dfrac{\mathrm{\pi }}{4} $ , $ k\in \boldsymbol{Z} $ ,又 $ |\varphi | < \dfrac{\mathrm{\pi }}{2} $ ,所以 $ \varphi =\dfrac{\mathrm{\pi }}{4} $ , $ \mathrm{B} $ 正确;
由上可知 $ f(x)= \sin (\dfrac{3}{2}x+\dfrac{\mathrm{\pi }}{4}) $ ,则 $ f(x+\dfrac{\mathrm{\pi }}{6})= \sin [\dfrac{3}{2}(x+\dfrac{\mathrm{\pi }}{6})+\dfrac{\mathrm{\pi }}{4}]= \sin (\dfrac{3}{2}x+\dfrac{\mathrm{\pi }}{2})= \cos \dfrac{3}{2}x $ 为偶函数, $ \mathrm{C} $ 正确;
令 $ -\dfrac{\mathrm{\pi }}{2}+2k\mathrm{\pi } < \dfrac{3}{2}x+\dfrac{\mathrm{\pi }}{4} < \dfrac{\mathrm{\pi }}{2}+2k\mathrm{\pi } $ , $ k\in \boldsymbol{Z} $ ,可得 $ -\dfrac{\mathrm{\pi }}{2}+\dfrac{4}{3}k\mathrm{\pi } < x < \dfrac{\mathrm{\pi }}{6}+\dfrac{4}{3}k\mathrm{\pi } $ , $ k\in \boldsymbol{Z} $ ,
取 $ k=0 $ ,可知函数 $ f(x) $ 在区间 $ (-\dfrac{\mathrm{\pi }}{2},\dfrac{\mathrm{\pi }}{6}) $ 上单调递增, $ \mathrm{D} $ 错误.
故选 $ \mathrm{B}\mathrm{C} $ .
10.(多选)我们平时听到的声音不只是一个音在响,而是许多个音的结合,称为复合音.复合音的产生是因为发声体在全段振动产生频率为 $ f $ 的基音的同时,其各部分如二分之一、三分之一、四分之一部分也在振动,产生的频率恰好是全段振动频率的倍数,如 $ 2f $ , $ 3f $ , $ 4f $ 等,这些音叫谐音.因为其振幅较小,一般不易单独听出来,所以我们听到的声音的函数为 $ y= \sin x+\dfrac{1}{2} \sin 2x+\dfrac{1}{3} \sin 3x+\dfrac{1}{4} \sin 4x+\cdots $ .则函数 $ y= \sin x+\dfrac{1}{2} \sin 2x+\dfrac{1}{3} \sin 3x $ 的周期不可能为( )(多选)
A. $ \mathrm{\pi } $
B. $ 2\mathrm{\pi } $
C. $ \dfrac{2\mathrm{\pi }}{3} $
D. $ \dfrac{\mathrm{\pi }}{2} $
答案:ACD
解析:设 $ f(x)= \sin x+\dfrac{1}{2} \sin 2x+\dfrac{1}{3} \sin 3x $ ,
对于 $ \mathrm{A} $ , $ f(x+\mathrm{\pi })= \sin (x+\mathrm{\pi })+\dfrac{1}{2} \sin [2(x+\mathrm{\pi })]+\dfrac{1}{3} \sin [3(x+\mathrm{\pi })]=- \sin x+\dfrac{1}{2} \sin 2x-\dfrac{1}{3} \sin 3x\ne f(x) $ ,故 $ \mathrm{A} $ 不可能;
对于 $ \mathrm{B} $ , $ f(x+2\mathrm{\pi })= \sin (x+2\mathrm{\pi })+\dfrac{1}{2} \sin [2(x+2\mathrm{\pi })]+\dfrac{1}{3} \sin [3(x+2\mathrm{\pi })]= \sin x+\dfrac{1}{2} \sin 2x+\dfrac{1}{3} \sin 3x=f(x) $ ,故 $ \mathrm{B} $ 可能;
对于 $ \mathrm{C} $ , $ f(x+\dfrac{2\mathrm{\pi }}{3})= \sin (x+\dfrac{2\mathrm{\pi }}{3})+\dfrac{1}{2} \sin [2(x+\dfrac{2\mathrm{\pi }}{3})]+\dfrac{1}{3} \sin [3(x+\dfrac{2\mathrm{\pi }}{3})]\ne f(x) $ ,故 $ \mathrm{C} $ 不可能;
对于 $ \mathrm{D} $ , $ f(x+\dfrac{\mathrm{\pi }}{2})= \sin (x+\dfrac{\mathrm{\pi }}{2})+\dfrac{1}{2} \sin [2(x+\dfrac{\mathrm{\pi }}{2})]+\dfrac{1}{3} \sin [3(x+\dfrac{\mathrm{\pi }}{2})]= \cos x-\dfrac{1}{2} \sin 2x-\dfrac{1}{3} \cos 3x\ne f(x) $ ,故 $ \mathrm{D} $ 不可能.故选 $ \mathrm{A}\mathrm{C}\mathrm{D} $ .
11.当 $ \varphi = $ 时,函数 $ f(x)= \sin (x+\varphi ) $ 在区间 $ (\dfrac{\mathrm{\pi }}{3},\dfrac{4\mathrm{\pi }}{3}) $ 上单调(写出一个值即可).
答案: $ \dfrac{\mathrm{\pi }}{6} $ (集合 $ {\varphi \mid \varphi =-\dfrac{5\mathrm{\pi }}{6}+2{k}_{1}\mathrm{\pi }\text{或}\varphi =\dfrac{\mathrm{\pi }}{6}+2{k}_{2}\mathrm{\pi },{k}_{1},{k}_{2}\in \boldsymbol{Z}} $ 中的任何一个值都行)
解析: $ \because f(x) $ 的周期是 $ 2\mathrm{\pi } $ ,且区间 $ (\dfrac{\mathrm{\pi }}{3},\dfrac{4\mathrm{\pi }}{3}) $ 的长度是 $ \mathrm{\pi } $ , $ \therefore (\dfrac{\mathrm{\pi }}{3},\dfrac{4\mathrm{\pi }}{3}) $ 是一个周期内完整的一个单调递增区间或单调递减区间.
当 $ \dfrac{\mathrm{\pi }}{3} < x < \dfrac{4\mathrm{\pi }}{3} $ 时, $ \dfrac{\mathrm{\pi }}{3}+\varphi < x+\varphi < \dfrac{4\mathrm{\pi }}{3}+\varphi $ , $ \text{ }\therefore \begin{cases}\dfrac{\mathrm{\pi }}{3}+\varphi =-\dfrac{\mathrm{\pi }}{2}+2{k}_{1}\mathrm{\pi },\\ \dfrac{4\mathrm{\pi }}{3}+\varphi =\dfrac{\mathrm{\pi }}{2}+2{k}_{1}\mathrm{\pi },\end{cases}{k}_{1}\in \boldsymbol{Z} $ ,
解得 $ \varphi =-\dfrac{5\mathrm{\pi }}{6}+2{k}_{1}\mathrm{\pi } $ , $ {k}_{1}\in \boldsymbol{Z} $ ,
或 $ \begin{cases}\dfrac{\mathrm{\pi }}{3}+\varphi =\dfrac{\mathrm{\pi }}{2}+2{k}_{2}\mathrm{\pi },\\ \dfrac{4\mathrm{\pi }}{3}+\varphi =\dfrac{3\mathrm{\pi }}{2}+2{k}_{2}\mathrm{\pi },\end{cases}{k}_{2}\in \boldsymbol{Z} $ ,
解得 $ \varphi =\dfrac{\mathrm{\pi }}{6}+2{k}_{2}\mathrm{\pi } $ , $ {k}_{2}\in \boldsymbol{Z} $ .
故 $ \varphi $ 可取 $ \dfrac{\mathrm{\pi }}{6} $ (集合 $ {\varphi \mid \varphi =-\dfrac{5\mathrm{\pi }}{6}+2{k}_{1}\mathrm{\pi }\text{或}\varphi =\dfrac{\mathrm{\pi }}{6}+2{k}_{2}\mathrm{\pi },{k}_{1},{k}_{2}\in \boldsymbol{Z}} $ 中的任何一个值都行)
12.已知 $ f(x) $ 是以 $ \mathrm{\pi } $ 为周期的偶函数,且当 $ x\in [0,\dfrac{\mathrm{\pi }}{2}] $ 时, $ f(x)=1- \sin \text{ }x $ ,则当 $ x\in [\dfrac{5\mathrm{\pi }}{2},3\mathrm{\pi }] $ 时, $ f(x)= $ .
答案: $ 1- \sin \text{ }x $
解析:当 $ x\in [\dfrac{5\mathrm{\pi }}{2},3\mathrm{\pi }] $ 时, $ 3\mathrm{\pi }-x\in [0,\dfrac{\mathrm{\pi }}{2}].\text{ }\because $ 当 $ x\in [0,\dfrac{\mathrm{\pi }}{2}] $ 时, $ f(x)=1- \sin \text{ }x $ , $ \text{ }\therefore f(3\mathrm{\pi }-x)=1- \sin (3\mathrm{\pi }-x)=1- \sin \text{ }x $ .
又 $ \because f(x) $ 是以 $ \mathrm{\pi } $ 为周期的偶函数,
$ \therefore f(3\mathrm{\pi }-x)=f(-x)=f(x) $ , $ \text{ }\therefore $ 当 $ x\in [\dfrac{5\mathrm{\pi }}{2},3\mathrm{\pi }] $ 时, $ f(x)=1- \sin \text{ }x $ .
13.已知 $ f(\alpha )=\dfrac{ \tan (\mathrm{\pi }-\alpha ) \sin (\mathrm{\pi }-\alpha ) \sin (\dfrac{\mathrm{\pi }}{2}+\alpha )}{ \cos (3\mathrm{\pi }+\alpha ) \cos (\dfrac{3\mathrm{\pi }}{2}-\alpha )} $ .
(1) 化简 $ f(\alpha ) $ ,并写出使 $ f(\alpha ) $ 有意义的实数 $ \alpha $ 的集合;
(2) 求函数 $ y=f(2x-\dfrac{\mathrm{\pi }}{3}) $ 的周期及满足 $ y=f(2x-\dfrac{\mathrm{\pi }}{3})\geqslant 1 $ 的实数 $ x $ 的集合.
答案:(1) 【解】因为 $ f(\alpha )= $
$ \dfrac{ \tan (\mathrm{\pi }-\alpha ) \sin (\mathrm{\pi }-\alpha ) \sin (\dfrac{\mathrm{\pi }}{2}+\alpha )}{ \cos (3\mathrm{\pi }+\alpha ) \cos (\dfrac{3\mathrm{\pi }}{2}-\alpha )}= $
$ \dfrac{- \tan \alpha \sin \alpha \cos \alpha }{- \cos \alpha (- \sin \alpha )}=- \tan \alpha $ ,
所以 $ \sin \alpha \ne 0 $ 且 $ \cos \alpha \ne 0 $ ,
故所求集合为 $ {\alpha |\alpha \ne \dfrac{k\mathrm{\pi }}{2},k\in \boldsymbol{Z}} $ .
(2) 【解】由(1)可知,函数 $ y=f(2x-\dfrac{\mathrm{\pi }}{3})=- \tan (2x-\dfrac{\mathrm{\pi }}{3}) $ ,
所以由正切函数的性质可得其周期为 $ \dfrac{\mathrm{\pi }}{2} $ .
$ f(2x-\dfrac{\mathrm{\pi }}{3})\geqslant 1 $ ,即 $ - \tan (2x-\dfrac{\mathrm{\pi }}{3})\geqslant 1 $ ,故 $ \tan (2x-\dfrac{\mathrm{\pi }}{3})\leqslant -1 $ ,
即 $ k\mathrm{\pi }-\dfrac{\mathrm{\pi }}{2} < 2x-\dfrac{\mathrm{\pi }}{3}\leqslant k\mathrm{\pi }-\dfrac{\mathrm{\pi }}{4} $ , $ k\in \boldsymbol{Z} $ ,
得 $ \dfrac{k\mathrm{\pi }}{2}-\dfrac{\mathrm{\pi }}{12} < x\leqslant \dfrac{k\mathrm{\pi }}{2}+\dfrac{\mathrm{\pi }}{24} $ , $ k\in \boldsymbol{Z} $ ,
故满足 $ y=f(2x-\dfrac{\mathrm{\pi }}{3})\geqslant 1 $ 的实数 $ x $ 的集合为 $ {x|\dfrac{k\mathrm{\pi }}{2}-\dfrac{\mathrm{\pi }}{12} < x\leqslant \dfrac{k\mathrm{\pi }}{2}+\dfrac{\mathrm{\pi }}{24},k\in \boldsymbol{Z}} $ .
解析:
14.设函数 $ f(x)=A \sin (2x+\varphi )(A > 0,0 < \varphi < \dfrac{\mathrm{\pi }}{2}) $ ,函数 $ f(x) $ 的最小值为 $ -2 $ ,且 $ x=\dfrac{\mathrm{\pi }}{3} $ 为函数 $ f(x) $ 的一个零点.
(1)求函数 $ f(x) $ 的单调递增区间;
(2)若对任意的 $ x\in [0,\dfrac{\mathrm{\pi }}{4}] $ ,不等式 $ f(x) > m-3 $ 恒成立,求实数 $ m $ 的取值范围.
解析:(1) $ \because f{(x)}_{ \min }=-A=-2 $ , $ \therefore A=2 $ .
$ \because x=\dfrac{\mathrm{\pi }}{3} $ 为 $ f(x) $ 的一个零点, $ \therefore \dfrac{2\mathrm{\pi }}{3}+\varphi =k\mathrm{\pi }(k\in \boldsymbol{Z}) $ ,解得 $ \varphi =k\mathrm{\pi }-\dfrac{2\mathrm{\pi }}{3}(k\in \boldsymbol{Z}) $ ,
又 $ 0 < \varphi < \dfrac{\mathrm{\pi }}{2} $ , $ \therefore \varphi =\dfrac{\mathrm{\pi }}{3} $ , $ \therefore f(x)=2 \sin (2x+\dfrac{\mathrm{\pi }}{3}) $ .
令 $ -\dfrac{\mathrm{\pi }}{2}+2k\mathrm{\pi }\leqslant 2x+\dfrac{\mathrm{\pi }}{3}\leqslant \dfrac{\mathrm{\pi }}{2}+2k\mathrm{\pi }(k\in \boldsymbol{Z}) $ ,解得 $ -\dfrac{5\mathrm{\pi }}{12}+k\mathrm{\pi }\leqslant x\leqslant \dfrac{\mathrm{\pi }}{12}+k\mathrm{\pi }(k\in \boldsymbol{Z}) $ ,
故 $ f(x) $ 的单调递增区间为 $ [-\dfrac{5\mathrm{\pi }}{12}+k\mathrm{\pi },\dfrac{\mathrm{\pi }}{12}+k\mathrm{\pi }](k\in \boldsymbol{Z}) $ .
(2)当 $ x\in [0,\dfrac{\mathrm{\pi }}{4}] $ 时, $ 2x+\dfrac{\mathrm{\pi }}{3}\in [\dfrac{\mathrm{\pi }}{3},\dfrac{5\mathrm{\pi }}{6}] $ , $ \therefore \sin (2x+\dfrac{\mathrm{\pi }}{3})\in [\dfrac{1}{2},1] $ , $ \therefore f(x)\in [1,2] $ .
$ \because $ 对任意的 $ x\in [0,\dfrac{\mathrm{\pi }}{4}] $ , $ f(x) > m-3 $ 恒成立, $ \therefore m-3 < f{(x)}_{ \min }=1 $ ,
解得 $ m < 4 $ ,即实数 $ m $ 的取值范围为 $ (-\mathrm{\infty },4) $ .




