课时1 两角和与差的正弦、余弦和正切公式
一、刷基础
1. $ \sin {20}^{\circ }· \cos {40}^{\circ }+ \cos {20}^{\circ } \cos {50}^{\circ } $ 的值是( )
A. $ \dfrac{\sqrt{3}}{2} $
B. $ \dfrac{1}{2} $
C. $ -\dfrac{1}{2} $
D.1
答案:A
解析:原式 $ = \sin {20}^{\circ } \cos {40}^{\circ }+ \cos {20}^{\circ } \sin {40}^{\circ }= \sin {60}^{\circ }=\dfrac{\sqrt{3}}{2} $ .故选 $ \mathrm{A} $ .
2.已知 $ \alpha $ 为第二象限角,且终边与单位圆的交点的横坐标为 $ -\dfrac{4}{5} $ ,则 $ \cos (\alpha -\dfrac{5\mathrm{\pi }}{4})= $ ( )
A. $ -\dfrac{7\sqrt{2}}{10} $
B. $ \dfrac{7\sqrt{2}}{10} $
C. $ -\dfrac{\sqrt{2}}{10} $
D. $ \dfrac{\sqrt{2}}{10} $
答案:D
解析:由题意,得 $ \cos \alpha =-\dfrac{4}{5} $ ,
则 $ \sin \alpha =\sqrt{1-{\left(-\dfrac{4}{5}\right) ^ {2}}}=\dfrac{3}{5} $ ,
所以 $ \cos (\alpha -\dfrac{5\mathrm{\pi }}{4})= \cos (\alpha +\dfrac{3\mathrm{\pi }}{4})= \cos \alpha \cdot \cos \dfrac{3\mathrm{\pi }}{4}- \sin \alpha \sin \dfrac{3\mathrm{\pi }}{4}=(-\dfrac{4}{5})×(-\dfrac{\sqrt{2}}{2})-\dfrac{3}{5}×\dfrac{\sqrt{2}}{2}=\dfrac{\sqrt{2}}{10} $ .
故选 $ \mathrm{D} $ .
3.若 $ \alpha +\beta =\dfrac{3\mathrm{\pi }}{4} $ ,则 $ (1- \tan \alpha )(1- \tan \beta )= $ ( )
A.0
B.1
C. $ \sqrt{3} $
D.2
答案:D
解析:因为 $ \alpha +\beta =\dfrac{3\mathrm{\pi }}{4} $ ,所以 $ \tan (\alpha +\beta )=\dfrac{ \tan \alpha + \tan \beta }{1- \tan \alpha \tan \beta }= \tan \dfrac{3\mathrm{\pi }}{4}=-1 $ ,
所以 $ \tan \alpha + \tan \beta = \tan \alpha \tan \beta -1 $ ,
所以 $ (1- \tan \alpha )(1- \tan \beta )=1-( \tan \alpha + \tan \beta )+ \tan \alpha \tan \beta =1-( \tan \alpha \tan \beta -1)+ \tan \alpha \tan \beta =2 $ .
故选 $ \mathrm{D} $ .
4.若 $ \alpha $ , $ \beta $ 都是锐角,且 $ \cos \text{ }\alpha =\dfrac{\sqrt{5}}{5} $ , $ \sin (\alpha -\beta )=\dfrac{\sqrt{10}}{10} $ ,则 $ \cos \text{ }\beta = $ ( )
A. $ \dfrac{\sqrt{2}}{2} $
B. $ \dfrac{\sqrt{2}}{10} $
C. $ -\dfrac{\sqrt{2}}{2} $ 或 $ -\dfrac{\sqrt{2}}{10} $
D. $ \dfrac{\sqrt{2}}{2} $ 或 $ \dfrac{\sqrt{2}}{10} $
答案:A
解析: $ \alpha $ , $ \beta $ 都是锐角,则 $ -\dfrac{\mathrm{\pi }}{2} < \alpha -\beta < \dfrac{\mathrm{\pi }}{2} $ .
由题意得 $ \cos (\alpha -\beta )=\sqrt{1-{\left(\dfrac{\sqrt{10}}{10}\right) ^ {2}}}=\dfrac{3\sqrt{10}}{10} $ , $ \sin \text{ }\alpha =\sqrt{1-{\left(\dfrac{\sqrt{5}}{5}\right) ^ {2}}}=\dfrac{2\sqrt{5}}{5} $ ,
$ \therefore \cos \text{ }\beta = \cos \text{ }[\alpha -(\alpha -\beta )]= \cos \text{ }\alpha \cos (\alpha -\beta )+ \sin \text{ }\alpha \sin (\alpha -\beta )=\dfrac{\sqrt{5}}{5}×\dfrac{3\sqrt{10}}{10}+\dfrac{2\sqrt{5}}{5}×\dfrac{\sqrt{10}}{10}=\dfrac{\sqrt{2}}{2} $ .故选 $ \mathrm{A} $ .
5.已知 $ 0 < \beta < \alpha < \dfrac{\mathrm{\pi }}{2} $ , $ \cos (\alpha -\beta )=\dfrac{3}{5} $ , $ \cos \alpha \cos \beta =\dfrac{1}{2} $ ,则 $ \dfrac{1}{ \tan \alpha }-\dfrac{1}{ \tan \beta }= $ ( )
A. $ -\dfrac{1}{10} $
B. $ \dfrac{8}{11} $
C. $ -4 $
D. $ -8 $
答案:D
解析:因为 $ 0 < \alpha < \dfrac{\mathrm{\pi }}{2} $ ,所以 $ -\dfrac{\mathrm{\pi }}{2} < -\alpha < 0 $ .又 $ 0 < \beta < \dfrac{\mathrm{\pi }}{2} $ ,所以 $ -\dfrac{\mathrm{\pi }}{2} < \beta -\alpha < \dfrac{\mathrm{\pi }}{2} $ .
又 $ \beta < \alpha $ ,所以 $ -\dfrac{\mathrm{\pi }}{2} < \beta -\alpha < 0 $ ,所以 $ \sin (\beta -\alpha ) < 0 $ .
又因为 $ \cos (\alpha -\beta )=\dfrac{3}{5} $ ,
所以 $ \sin (\beta -\alpha )=-\sqrt{1-{ \cos }^{2}(\beta -\alpha )}=-\dfrac{4}{5} $ ,
且 $ \cos (\alpha -\beta )= \cos \alpha \cos \beta + \sin \alpha \sin \beta =\dfrac{3}{5} $ ,
又 $ \cos \alpha \cos \beta =\dfrac{1}{2} $ ,所以 $ \sin \alpha \sin \beta =\dfrac{3}{5}-\dfrac{1}{2}=\dfrac{1}{10} $ ,
所以 $ \dfrac{1}{ \tan \alpha }-\dfrac{1}{ \tan \beta }=\dfrac{ \cos \alpha }{ \sin \alpha }-\dfrac{ \cos \beta }{ \sin \beta }=\dfrac{ \cos \alpha \sin \beta - \cos \beta \sin \alpha }{ \sin \alpha \sin \beta }=\dfrac{ \sin (\beta -\alpha )}{ \sin \alpha \sin \beta }=\dfrac{-\dfrac{4}{5}}{\dfrac{1}{10}}=-8 $ .故选 $ \mathrm{D} $ .
6.已知 $ A $ , $ B $ , $ C $ 是 $ △ABC $ 的三个内角, $ \sin \text{ }A=\dfrac{3}{5} $ , $ \cos \text{ }B=-\dfrac{1}{2} $ ,则 $ \sin \text{ }C $ .
答案: $ \dfrac{4\sqrt{3}-3}{10} $
解析:由 $ \sin \text{ }A=\dfrac{3}{5} $ , $ \cos \text{ }B=-\dfrac{1}{2} < 0 $ ,得 $ B $ 为钝角, $ A $ , $ C $ 为锐角,故 $ \cos \text{ }A=\dfrac{4}{5} $ , $ \sin \text{ }B=\dfrac{\sqrt{3}}{2} $ .
故 $ \sin \text{ }C= \sin (A+B)= \sin \text{ }A \cos \text{ }B+ \cos \text{ }A \sin \text{ }B=\dfrac{3}{5}×(-\dfrac{1}{2})+\dfrac{4}{5}×\dfrac{\sqrt{3}}{2}=\dfrac{4\sqrt{3}-3}{10} $ .
7.在 $ △ABC $ 中,内角 $ A $ , $ B $ , $ C $ 满足 $ \dfrac{ \cos A}{ \cos B}=\dfrac{2}{1- \tan A \tan C} $ ,则角 $ C $ 的大小是( )
A. $ \dfrac{\mathrm{\pi }}{6} $
B. $ \dfrac{\mathrm{\pi }}{3} $
C. $ \dfrac{2\mathrm{\pi }}{3} $
D. $ \dfrac{5\mathrm{\pi }}{6} $
答案:C
解析:因为 $ \dfrac{ \cos A}{ \cos B}=\dfrac{2}{1- \tan A \tan C} $ ,
所以 $ \cos A-\dfrac{ \sin A \sin C}{ \cos C}=2 \cos B $ ,
故 $ \cos A \cos C- \sin A \sin C=2 \cos B \cos C $ ,
故 $ \cos (A+C)=2 \cos B \cos C $ ,
故 $ - \cos B=2 \cos B \cos C $ ,
由题设知 $ \cos B\ne 0 $ ,故 $ \cos C=-\dfrac{1}{2} $ .
又 $ C\in (0,\mathrm{\pi }) $ ,所以 $ C=\dfrac{2\mathrm{\pi }}{3} $ .故选 $ \mathrm{C} $ .
8.已知 $ \alpha $ , $ \beta $ 都是锐角,且 $ \cos \text{ }\alpha =\dfrac{\sqrt{10}}{10} $ , $ \cos \text{ }\beta =\dfrac{\sqrt{5}}{5} $ ,则 $ \alpha +\beta = $ ( )
A. $ \dfrac{\mathrm{\pi }}{4} $
B. $ \dfrac{3\mathrm{\pi }}{4} $
C. $ \dfrac{\mathrm{\pi }}{3} $
D. $ \dfrac{2\mathrm{\pi }}{3} $
答案:B
解析:因为 $ \alpha $ , $ \beta $ 都是锐角,且 $ \cos \text{ }\alpha =\dfrac{\sqrt{10}}{10} $ , $ \cos \text{ }\beta =\dfrac{\sqrt{5}}{5} $ ,
所以 $ \sin \text{ }\alpha =\dfrac{3\sqrt{10}}{10} $ , $ \sin \text{ }\beta =\dfrac{2\sqrt{5}}{5} $ ,
所以 $ \cos (\alpha +\beta )= \cos \text{ }\alpha \cos \text{ }\beta - \sin \text{ }\alpha \sin \text{ }\beta =-\dfrac{\sqrt{2}}{2} $ .
又 $ \alpha +\beta \in (0,\mathrm{\pi }) $ ,所以 $ \alpha +\beta =\dfrac{3\mathrm{\pi }}{4} $ ,故选 $ \mathrm{B} $ .
9.在 $ △ABC $ 中, $ \tan A $ 和 $ \tan B $ 是关于 $ x $ 的方程 $ {x}^{2}-{ \sin }^{2}\theta \cdot x+{ \cos }^{2}\theta =0 $ 的两根,则 $ C= $ .
答案: $ \dfrac{3\mathrm{\pi }}{4} $
解析:由题意得 $ \tan A+ \tan B={ \sin }^{2}\theta $ , $ \tan A\cdot \tan B={ \cos }^{2}\theta $ ,
所以 $ \tan (A+B)=\dfrac{ \tan A+ \tan B}{1- \tan A\cdot \tan B}=\dfrac{{ \sin }^{2}\theta }{1-{ \cos }^{2}\theta }=1 $ ,
由 $ \tan (A+B)= \tan (\mathrm{\pi }-C)=- \tan C $ ,
得 $ \tan C=-1 $ ,
又 $ 0 < C < \mathrm{\pi } $ ,所以 $ C=\dfrac{3\mathrm{\pi }}{4} $ .
10. $ \sqrt{3} \sin {15}^{\circ }+ \sin {75}^{\circ }= $ ( )
A. $ \dfrac{\sqrt{2}}{2} $
B.1
C. $ \sqrt{2} $
D. $ \dfrac{\sqrt{6}}{2} $
答案:C
解析: $ \sqrt{3} \sin {15}^{\circ }+ \sin {75}^{\circ }=\sqrt{3} \sin {15}^{\circ }+ \cos {15}^{\circ }=2 \sin ({15}^{\circ }+{30}^{\circ })=2 \sin {45}^{\circ }=\sqrt{2} $ .故选 $ \mathrm{C} $ .
11.已知函数 $ f(x)= \sin \omega x-\sqrt{3} \cos \omega x+1(\omega > 0) $ ,若对任意 $ \lambda \in \boldsymbol{R} $ , $ f(x) $ 在区间 $ (\lambda ,\lambda +\dfrac{2\mathrm{\pi }}{3}) $ 上的值域均为 $ [-1,3] $ ,则 $ \omega $ 的取值范围为( )
A. $ (3,+\mathrm{\infty }) $
B. $ (\dfrac{1}{3},+\mathrm{\infty }) $
C. $ (0,3) $
D. $ (0,\dfrac{1}{3}) $
答案:A
解析:因为 $ f(x)= \sin \omega x-\sqrt{3} \cos \omega x+1=2 \sin (\omega x-\dfrac{\mathrm{\pi }}{3})+1 $ ,
当 $ x\in \boldsymbol{R} $ 时, $ \sin (\omega x-\dfrac{\mathrm{\pi }}{3})\in [-1,1] $ ,故 $ f(x)\in [-1,3] $ .
因为 $ \forall \lambda \in \boldsymbol{R} $ , $ f(x) $ 在 $ (\lambda ,\lambda +\dfrac{2\mathrm{\pi }}{3}) $ 上的值域均为 $ [-1,3] $ ,
所以区间长度 $ \dfrac{2\mathrm{\pi }}{3} $ 必须大于一个周期,
即 $ \dfrac{2\mathrm{\pi }}{3} > \dfrac{2\mathrm{\pi }}{\omega } $ ,解得 $ \omega > 3 $ .故选 $ \mathrm{A} $ .
二、刷提升
1. $ \dfrac{ \cos {20}^{\circ }-2 \sin {10}^{\circ }}{2 \sin {20}^{\circ }}= $ ( )
A. $ \dfrac{\sqrt{3}}{2} $
B. $ \sqrt{2} $
C. $ \sqrt{3} $
D.2
答案:A
解析: $ \dfrac{ \cos {20}^{\circ }-2 \sin {10}^{\circ }}{2 \sin {20}^{\circ }}=\dfrac{ \cos {20}^{\circ }-2 \sin ({30}^{\circ }-{20}^{\circ })}{2 \sin {20}^{\circ }}=\dfrac{ \cos {20}^{\circ }- \cos {20}^{\circ }+\sqrt{3} \sin {20}^{\circ }}{2 \sin {20}^{\circ }}=\dfrac{\sqrt{3}}{2} $ .
故选 $ \mathrm{A} $ .
2.已知锐角 $ \alpha $ , $ \beta $ 满足 $ \sin \alpha + \sin \alpha \sin \beta = \cos \alpha \cos \beta $ ,则 $ 2\alpha +\beta = $ ( )
A. $ \dfrac{\mathrm{\pi }}{4} $
B. $ \dfrac{\mathrm{\pi }}{3} $
C. $ \dfrac{\mathrm{\pi }}{2} $
D. $ \mathrm{\pi } $
答案:C
解析:由 $ \sin \alpha + \sin \alpha \sin \beta = \cos \alpha \cos \beta $ ,得 $ \sin \alpha = \cos \alpha \cos \beta - \sin \alpha \sin \beta = \cos (\alpha +\beta ) $ ,
因此 $ \cos (\dfrac{\mathrm{\pi }}{2}-\alpha )= \cos (\alpha +\beta ) $ ,由 $ 0 < \alpha < \dfrac{\mathrm{\pi }}{2} $ , $ 0 < \beta < \dfrac{\mathrm{\pi }}{2} $ ,得 $ 0 < \dfrac{\mathrm{\pi }}{2}-\alpha < \dfrac{\mathrm{\pi }}{2} $ , $ 0 < \alpha +\beta < \mathrm{\pi } $ ,
又余弦函数 $ y= \cos x $ 在 $ (0,\mathrm{\pi }) $ 上单调递减,所以 $ \dfrac{\mathrm{\pi }}{2}-\alpha =\alpha +\beta $ ,所以 $ 2\alpha +\beta =\dfrac{\mathrm{\pi }}{2} $ .故选 $ \mathrm{C} $ .
3.若 $ \cos (\alpha -\beta )=\dfrac{\sqrt{5}}{5} $ , $ \cos 2\alpha =\dfrac{\sqrt{10}}{10} $ ,并且 $ \alpha $ , $ \beta $ 均为锐角,且 $ \alpha < \beta $ ,则 $ \alpha +\beta $ 的值为( )
A. $ \dfrac{\mathrm{\pi }}{6} $
B. $ \dfrac{\mathrm{\pi }}{4} $
C. $ \dfrac{3\mathrm{\pi }}{4} $
D. $ \dfrac{5\mathrm{\pi }}{6} $
答案:C
解析:因为 $ \cos (\alpha -\beta )=\dfrac{\sqrt{5}}{5} $ , $ \cos 2\alpha =\dfrac{\sqrt{10}}{10} $ ,并且 $ \alpha $ , $ \beta $ 均为锐角,且 $ \alpha < \beta $ ,
所以 $ \alpha -\beta \in (-\dfrac{\mathrm{\pi }}{2},0) $ , $ 2\alpha \in (0,\dfrac{\mathrm{\pi }}{2}) $ ,
所以 $ \sin (\alpha -\beta )=-\sqrt{1-{ \cos }^{2}(\alpha -\beta )}=-\dfrac{2\sqrt{5}}{5} $ , $ \sin 2\alpha =\sqrt{1-{ \cos }^{2}2\alpha }=\dfrac{3\sqrt{10}}{10} $ ,
则 $ \cos (\alpha +\beta )= \cos [2\alpha -(\alpha -\beta )]= \cos 2\alpha \cos (\alpha -\beta )+ \sin 2\alpha \sin (\alpha -\beta )=\dfrac{\sqrt{10}}{10}×\dfrac{\sqrt{5}}{5}+\dfrac{3\sqrt{10}}{10}×(-\dfrac{2\sqrt{5}}{5})=-\dfrac{\sqrt{2}}{2} $ .
又因为 $ \alpha +\beta \in (0,\mathrm{\pi }) $ ,所以 $ \alpha +\beta =\dfrac{3\mathrm{\pi }}{4} $ .故选 $ \mathrm{C} $ .
4.希腊数学家泰特托斯( $ \mathrm{T}\mathrm{h}\mathrm{e}\mathrm{a}\mathrm{e}\mathrm{t}\mathrm{e}\mathrm{t}\mathrm{u}\mathrm{s} $ ,公元前 $ 417— $ 公元前369年)详细地讨论了无理数的理论,他通过如图来构造无理数 $ \sqrt{2} $ , $ \sqrt{3} $ , $ \sqrt{5} $ , $ \cdots $ ,则 $ \sin \mathrm{\angle }BAD= $ ( )
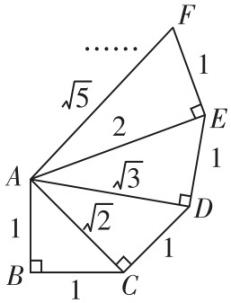
A. $ \dfrac{2\sqrt{6}+3\sqrt{3}}{6} $
B. $ \dfrac{2\sqrt{6}-3\sqrt{3}}{6} $
C. $ \dfrac{2\sqrt{3}+\sqrt{6}}{6} $
D. $ \dfrac{2\sqrt{3}-\sqrt{6}}{6} $
答案:C
解析:记 $ \mathrm{\angle }BAC=\alpha $ , $ \mathrm{\angle }CAD=\beta $ ,
由题图知 $ \sin \alpha = \cos \alpha =\dfrac{\sqrt{2}}{2} $ , $ \cos \beta =\dfrac{\sqrt{6}}{3} $ , $ \sin \beta =\dfrac{\sqrt{3}}{3} $ ,
所以 $ \sin \mathrm{\angle }BAD= \sin (\mathrm{\angle }BAC+\mathrm{\angle }CAD)= \sin (\alpha +\beta )= \sin \alpha \cos \beta + \cos \alpha \sin \beta =\dfrac{\sqrt{2}}{2}×\dfrac{\sqrt{6}}{3}+\dfrac{\sqrt{2}}{2}×\dfrac{\sqrt{3}}{3}=\dfrac{2\sqrt{3}+\sqrt{6}}{6} $ .故选 $ \mathrm{C} $ .
5.已知 $ \cos (\dfrac{\mathrm{\pi }}{2}-\alpha )=2 \cos (\mathrm{\pi }+\alpha ) $ ,且 $ \tan (\alpha +\beta )=\dfrac{1}{3} $ ,则 $ \tan \text{ }\beta $ 的值为( )
A. $ -7 $
B.7
C.1
D. $ -1 $
答案:B
解析: $ \because \cos (\dfrac{\mathrm{\pi }}{2}-\alpha )=2 \cos (\mathrm{\pi }+\alpha ) $ , $ \therefore \sin \text{ }\alpha =-2 \cos \text{ }\alpha $ ,即 $ \tan \text{ }\alpha =-2 $ .
又 $ \because \tan (\alpha +\beta )=\dfrac{ \tan \text{ }\alpha + \tan \text{ }\beta }{1- \tan \text{ }\alpha \tan \text{ }\beta }=\dfrac{-2+ \tan \text{ }\beta }{1+2 \tan \text{ }\beta }=\dfrac{1}{3} $ , $ \therefore \tan \text{ }\beta =7 $ .故选 $ \mathrm{B} $ .
6.已知函数 $ f(x)= \sin \text{ }x+\sqrt{3} \cos \text{ }x $ ,当 $ x=\alpha $ 时,函数 $ f(x) $ 取得最大值,则 $ \sin (\alpha -\dfrac{\mathrm{\pi }}{4})= $ ( )
A. $ \dfrac{\sqrt{2}+\sqrt{6}}{4} $
B. $ \dfrac{\sqrt{2}-\sqrt{6}}{4} $
C. $ \dfrac{\sqrt{6}-\sqrt{2}}{4} $
D. $ -\dfrac{\sqrt{2}+\sqrt{6}}{4} $
答案:B
解析: $ f(x)= \sin \text{ }x+\sqrt{3} \cos \text{ }x=2 \sin (x+\dfrac{\mathrm{\pi }}{3}) $ ,其取最大值时,有 $ x+\dfrac{\mathrm{\pi }}{3}=\dfrac{\mathrm{\pi }}{2}+2k\mathrm{\pi }(k\in \boldsymbol{Z}) $ ,所以 $ x=\alpha =\dfrac{\mathrm{\pi }}{6}+2k\mathrm{\pi }(k\in \boldsymbol{Z}) $ .
所以 $ \sin (\alpha -\dfrac{\mathrm{\pi }}{4})= \sin (\dfrac{\mathrm{\pi }}{6}+2k\mathrm{\pi }-\dfrac{\mathrm{\pi }}{4})\text{ } $
$ = \sin (\dfrac{\mathrm{\pi }}{6}-\dfrac{\mathrm{\pi }}{4})\text{ } $
$ = \sin \dfrac{\mathrm{\pi }}{6} \cos \dfrac{\mathrm{\pi }}{4}- \cos \dfrac{\mathrm{\pi }}{6} \sin \dfrac{\mathrm{\pi }}{4}\text{ } $
$ =\dfrac{\sqrt{2}-\sqrt{6}}{4} $ .
故选 $ \mathrm{B} $ .
7.已知 $ x\in (0,\dfrac{\mathrm{\pi }}{2}) $ , $ y\in (0,\dfrac{\mathrm{\pi }}{2}) $ , $ \dfrac{ \cos \text{ }x+ \sin \text{ }x}{ \cos \text{ }x- \sin \text{ }x}= \tan \text{ }y $ ,则( )
A. $ y-x=\dfrac{\mathrm{\pi }}{4} $
B. $ 2y-x=\dfrac{\mathrm{\pi }}{4} $
C. $ y-x=\dfrac{\mathrm{\pi }}{2} $
D. $ 2y-x=\dfrac{\mathrm{\pi }}{2} $
答案:A
解析:由题意知 $ \cos \text{ }x\ne 0 $ ,
则 $ \dfrac{ \cos \text{ }x+ \sin \text{ }x}{ \cos \text{ }x- \sin \text{ }x}= \tan \text{ }y $ ,即 $ \dfrac{1+ \tan \text{ }x}{1- \tan \text{ }x}= \tan \text{ }y $ ,
所以 $ \dfrac{ \tan \dfrac{\mathrm{\pi }}{4}+ \tan \text{ }x}{1- \tan \text{ }x\cdot \tan \dfrac{\mathrm{\pi }}{4}}= \tan \text{ }y $ ,
即 $ \tan (x+\dfrac{\mathrm{\pi }}{4})= \tan \text{ }y $ ,
又 $ x\in (0,\dfrac{\mathrm{\pi }}{2}) $ , $ y\in (0,\dfrac{\mathrm{\pi }}{2}) $ ,
则 $ \dfrac{\mathrm{\pi }}{4} < x+\dfrac{\mathrm{\pi }}{4} < \dfrac{3\mathrm{\pi }}{4} $ , $ \tan \text{ }y > 0 $ ,
所以 $ \tan (x+\dfrac{\mathrm{\pi }}{4}) > 0 $ ,则 $ \dfrac{\mathrm{\pi }}{4} < x+\dfrac{\mathrm{\pi }}{4} < \dfrac{\mathrm{\pi }}{2} $ ,
所以有 $ x+\dfrac{\mathrm{\pi }}{4}=y $ ,即 $ y-x=\dfrac{\mathrm{\pi }}{4} $ .
故选 $ \mathrm{A} $ .
8.已知函数 $ f(x)= \sin \text{ }\mathrm{\pi }\omega x-\sqrt{3} \cos \text{ }\mathrm{\pi }\omega x(\omega > 0) $ 在 $ [0,1] $ 内恰有3个最值点和4个零点,则实数 $ \omega $ 的取值范围是( )
A. $ (\dfrac{10}{3},\dfrac{23}{6}] $
B. $ [\dfrac{10}{3},\dfrac{23}{6}) $
C. $ [\dfrac{17}{6},\dfrac{13}{3}) $
D. $ (\dfrac{17}{6},\dfrac{23}{6}] $
答案:B
解析: $ f(x)= \sin $ $ \mathrm{\pi }\omega x-\sqrt{3} \cos \text{ }\mathrm{\pi }\omega x=2 \sin (\mathrm{\pi }\omega x-\dfrac{\mathrm{\pi }}{3}) $ ,因为 $ x\in [0,1] $ 且 $ \omega > 0 $ ,
所以 $ \mathrm{\pi }\omega x-\dfrac{\mathrm{\pi }}{3}\in [-\dfrac{\mathrm{\pi }}{3},\omega \mathrm{\pi }-\dfrac{\mathrm{\pi }}{3}] $ .
又因为函数 $ f(x)= \sin \text{ }\mathrm{\pi }\omega x-\sqrt{3} \cos \text{ }\mathrm{\pi }\omega x(\omega > 0) $ 在 $ [0,1] $ 内恰有3个最值点和4个零点,所以由 $ y= \sin \text{ }x $ 的图象得 $ 3\mathrm{\pi }\leqslant \omega \mathrm{\pi }-\dfrac{\mathrm{\pi }}{3} < \dfrac{7\mathrm{\pi }}{2} $ ,解得 $ \dfrac{10}{3}\leqslant \omega < \dfrac{23}{6} $ .
所以实数 $ \omega $ 的取值范围是 $ [\dfrac{10}{3},\dfrac{23}{6}) $ .
故选 $ \mathrm{B} $ .
9.(多选)下列各式中,计算结果为 $ \sqrt{3} $ 的是( )(多选)
A. $ \cos {85}^{\circ } \cos {25}^{\circ }- \sin {85}^{\circ } \sin {25}^{\circ } $
B. $ \tan {25}^{\circ }+ \tan {35}^{\circ }+\sqrt{3} \tan {25}^{\circ } \tan {35}^{\circ } $
C. $ \dfrac{ \sin {15}^{\circ }+ \cos {15}^{\circ }}{ \cos {15}^{\circ }- \sin {15}^{\circ }} $
D. $ \dfrac{ \sin {40}^{\circ }+ \sin {80}^{\circ }}{ \cos {20}^{\circ }} $
答案:BCD
解析:对于 $ \mathrm{A} $ , $ \cos {85}^{\circ } \cos {25}^{\circ }- \sin {85}^{\circ } \sin {25}^{\circ }= \cos ({85}^{\circ }+{25}^{\circ })= \cos {110}^{\circ } < 0 $ ,故 $ \mathrm{A} $ 错误;
对于 $ \mathrm{B} $ , $ \tan {60}^{\circ }= \tan ({35}^{\circ }+{25}^{\circ })=\dfrac{ \tan {35}^{\circ }+ \tan {25}^{\circ }}{1- \tan {25}^{\circ } \tan {35}^{\circ }}=\sqrt{3} $ ,
所以 $ \tan {25}^{\circ }+ \tan {35}^{\circ }=-\sqrt{3} \tan {25}^{\circ } \tan {35}^{\circ }+\sqrt{3} $ ,所以 $ \tan {25}^{\circ }+ \tan {35}^{\circ }+\sqrt{3} \tan {25}^{\circ } \tan {35}^{\circ }=\sqrt{3} $ ,故 $ \mathrm{B} $ 正确;
对于 $ \mathrm{C} $ , $ \dfrac{ \sin {15}^{\circ }+ \cos {15}^{\circ }}{ \cos {15}^{\circ }- \sin {15}^{\circ }}=\dfrac{ \tan {15}^{\circ }+1}{1- \tan {15}^{\circ }}=\dfrac{ \tan {15}^{\circ }+ \tan {45}^{\circ }}{1- \tan {15}^{\circ } \tan {45}^{\circ }}= \tan ({15}^{\circ }+{45}^{\circ })= \tan {60}^{\circ }=\sqrt{3} $ ,故 $ \mathrm{C} $ 正确;
对于 $ \mathrm{D} $ , $ \dfrac{ \sin {40}^{\circ }+ \sin {80}^{\circ }}{ \cos {20}^{\circ }}=\dfrac{ \sin ({60}^{\circ }-{20}^{\circ })+ \sin ({60}^{\circ }+{20}^{\circ })}{ \cos {20}^{\circ }}=\dfrac{\dfrac{\sqrt{3}}{2} \cos {20}^{\circ }-\dfrac{1}{2} \sin {20}^{\circ }+\dfrac{\sqrt{3}}{2} \cos {20}^{\circ }+\dfrac{1}{2} \sin {20}^{\circ }}{ \cos {20}^{\circ }}=\dfrac{\sqrt{3} \cos {20}^{\circ }}{ \cos {20}^{\circ }}=\sqrt{3} $ ,故 $ \mathrm{D} $ 正确.故选 $ \mathrm{B}\mathrm{C}\mathrm{D} $ .
10.(多选)关于 $ △ABC $ ,下列说法正确的是( )(多选)
A.若 $ \sin 2A= \sin 2B $ ,则 $ △ABC $ 是等腰三角形
B. $ \tan A \tan B \tan C= \tan A+ \tan B+ \tan C $
C.若 $ △ABC $ 为锐角三角形,则 $ \sin A > \cos B $ 恒成立
D.若 $ \sin A+ \cos A=\dfrac{\sqrt{5}}{5} $ ,则 $ △ABC $ 为钝角三角形
答案:BCD
解析:对于 $ \mathrm{A} $ 选项,由于 $ 2A $ , $ 2B\in (0,2\mathrm{\pi }) $ ,因此若 $ \sin 2A= \sin 2B $ ,则有 $ 2A=2B $ 或 $ 2A+2B=\mathrm{\pi } $ ,得 $ A=B $ 或 $ A+B=\dfrac{\mathrm{\pi }}{2} $ ,因此 $ △ABC $ 为等腰三角形或直角三角形, $ \mathrm{A} $ 错误.
对于 $ \mathrm{B} $ 选项,在 $ △ABC $ 中, $ \tan C=- \tan (A+B)=\dfrac{ \tan A+ \tan B}{ \tan A \tan B-1} $ ,整理得 $ \tan A \tan B \tan C= \tan A+ \tan B+ \tan C $ , $ \mathrm{B} $ 正确.
对于 $ \mathrm{C} $ 选项,若 $ △ABC $ 为锐角三角形,则有 $ A+B=\mathrm{\pi }-C > \dfrac{\mathrm{\pi }}{2} $ ,故 $ A > \dfrac{\mathrm{\pi }}{2}-B $ ,且 $ A $ , $ \dfrac{\mathrm{\pi }}{2}-B\in (0,\dfrac{\mathrm{\pi }}{2}) $ ,由 $ y= \sin x $ 在 $ (0,\dfrac{\mathrm{\pi }}{2}) $ 上单调递增可得 $ \sin A > \sin (\dfrac{\mathrm{\pi }}{2}-B)= \cos B $ , $ \mathrm{C} $ 正确.
对于 $ \mathrm{D} $ 选项, $ ( \sin A+ \cos A)^{2}=1+2 \sin A \cos A=\dfrac{1}{5}⇒ \sin A \cos A=-\dfrac{2}{5} $ ,由 $ A\in (0,\mathrm{\pi }) $ 可得 $ \sin A > 0 $ ,故 $ \cos A < 0 $ ,因此 $ A\in (\dfrac{\mathrm{\pi }}{2},\mathrm{\pi }) $ ,则 $ △ABC $ 为钝角三角形, $ \mathrm{D} $ 正确.故选 $ \mathrm{B}\mathrm{C}\mathrm{D} $ .
11.(多选)已知函数 $ f(x)=| \sin x+\sqrt{3} \cos x| $ ,则( )(多选)
A. $ \mathrm{\pi } $ 是 $ f(x) $ 的一个周期
B.直线 $ x=\dfrac{\mathrm{\pi }}{2} $ 是 $ f(x) $ 图象的一条对称轴
C. $ f(x) $ 的值域为 $ [0,2] $
D. $ f(x) $ 在 $ [\dfrac{\mathrm{\pi }}{2},\dfrac{3\mathrm{\pi }}{2}] $ 上单调递减
答案:AC
解析:由 $ f(x)=| \sin x+\sqrt{3} \cos x|=|2 \sin (x+\dfrac{\mathrm{\pi }}{3})| $ ,又 $ y=2 \sin (x+\dfrac{\mathrm{\pi }}{3}) $ 的最小正周期 $ T=2\mathrm{\pi } $ ,
而 $ f(x)=|2 \sin (x+\dfrac{\mathrm{\pi }}{3})| $ 的图象是由 $ y=2 \sin (x+\dfrac{\mathrm{\pi }}{3}) $ 的图象将 $ x $ 轴下方部分翻折到 $ x $ 轴上方, $ x $ 轴及 $ x $ 轴上方部分不变而得到的,则 $ f(x) $ 的图象如图所示,
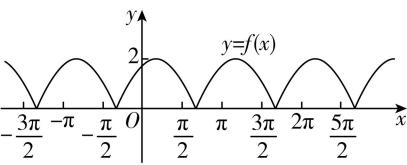
所以 $ f(x)=|2 \sin (x+\dfrac{\mathrm{\pi }}{3})| $ 的最小正周期为 $ \dfrac{1}{2}T=\mathrm{\pi } $ ,故 $ \mathrm{A} $ 正确;
因为 $ f(\dfrac{\mathrm{\pi }}{2})=|2 \sin (\dfrac{\mathrm{\pi }}{2}+\dfrac{\mathrm{\pi }}{3})|=1 $ ,所以直线 $ x=\dfrac{\mathrm{\pi }}{2} $ 不是 $ f(x) $ 图象的对称轴,故 $ \mathrm{B} $ 错误;
因为 $ \sin x\in [-1,1] $ ,所以 $ 2 \sin (x+\dfrac{\mathrm{\pi }}{3})\in [-2,2] $ ,所以 $ f(x)=|2 \sin (x+\dfrac{\mathrm{\pi }}{3})|\in [0,2] $ ,
故 $ f(x) $ 的值域为 $ [0,2] $ ,故 $ \mathrm{C} $ 正确;
因为 $ f(\dfrac{\mathrm{\pi }}{2})=1 $ , $ f(\dfrac{2\mathrm{\pi }}{3})=|2 \sin (\dfrac{2\mathrm{\pi }}{3}+\dfrac{\mathrm{\pi }}{3})|=0 $ , $ f(\mathrm{\pi })=|2 \sin (\mathrm{\pi }+\dfrac{\mathrm{\pi }}{3})|=\sqrt{3} $ ,所以 $ f(x) $ 在 $ [\dfrac{\mathrm{\pi }}{2},\dfrac{3\mathrm{\pi }}{2}] $ 上不单调,故 $ \mathrm{D} $ 错误.故选 $ \mathrm{A}\mathrm{C} $ .
12.化简: $ \tan {10}^{\circ }+ \tan {20}^{\circ }+2 \tan {30}^{\circ }+ \tan {10}^{\circ } \tan {20}^{\circ }\cdot \tan {30}^{\circ }= $ ; $ \dfrac{ \tan {12}^{\circ }+ \tan {18}^{\circ }+ \tan {150}^{\circ }}{ \tan {12}^{\circ } \tan {18}^{\circ }}= $ .
答案: $ \sqrt{3} $ ; $ -\dfrac{\sqrt{3}}{3} $
解析:因为 $ \tan {30}^{\circ }= \tan ({10}^{\circ }+{20}^{\circ })=\dfrac{ \tan {10}^{\circ }+ \tan {20}^{\circ }}{1- \tan {10}^{\circ } \tan {20}^{\circ }} $ ,
故 $ \tan {10}^{\circ }+ \tan {20}^{\circ }= \tan {30}^{\circ }- \tan {30}^{\circ }\cdot \tan {10}^{\circ } \tan {20}^{\circ } $ ,所以 $ \tan {10}^{\circ }+ \tan {20}^{\circ }+2 \tan {30}^{\circ }+ \tan {10}^{\circ }\cdot \tan {20}^{\circ } \tan {30}^{\circ }= \tan {30}^{\circ }- \tan {30}^{\circ } \tan {10}^{\circ }\cdot \tan {20}^{\circ }+2 \tan {30}^{\circ }+ \tan {10}^{\circ } \tan {20}^{\circ } \tan {30}^{\circ }=3 \tan {30}^{\circ }=\sqrt{3} $ .
因为 $ \tan {30}^{\circ }= \tan ({12}^{\circ }+{18}^{\circ })=\dfrac{ \tan {12}^{\circ }+ \tan {18}^{\circ }}{1- \tan {12}^{\circ } \tan {18}^{\circ }} $ ,所以 $ \tan {12}^{\circ }+ \tan {18}^{\circ }= \tan {30}^{\circ }(1- \tan {12}^{\circ } \tan {18}^{\circ }) $ ,所以
$ \dfrac{ \tan {12}^{\circ }+ \tan {18}^{\circ }+ \tan {150}^{\circ }}{ \tan {12}^{\circ } \tan {18}^{\circ }}=\dfrac{ \tan {30}^{\circ }(1- \tan {12}^{\circ } \tan {18}^{\circ })+ \tan ({180}^{\circ }-{30}^{\circ })}{ \tan {12}^{\circ } \tan {18}^{\circ }}=\dfrac{ \tan {30}^{\circ }(1- \tan {12}^{\circ } \tan {18}^{\circ })- \tan {30}^{\circ }}{ \tan {12}^{\circ } \tan {18}^{\circ }}=\dfrac{- \tan {30}^{\circ } \tan {12}^{\circ } \tan {18}^{\circ }}{ \tan {12}^{\circ } \tan {18}^{\circ }}=- \tan {30}^{\circ }=-\dfrac{\sqrt{3}}{3} $ .
13.若不等式 $ 2a- \sin x+a \cos x\geqslant 0 $ 对 $ x\in \boldsymbol{R} $ 恒成立,则实数 $ a $ 的取值范围是 .
答案: $ [\dfrac{\sqrt{3}}{3},+\mathrm{\infty }) $
解析:因为 $ 2a- \sin x+a \cos x\geqslant 0 $ ,则 $ 2a\geqslant \sin x-a \cos x=\sqrt{{a}^{2}+1}\cdot \sin (x-\varphi ) $ ,
其中 $ \sin \varphi =\dfrac{a}{\sqrt{{a}^{2}+1}} $ , $ \cos \varphi =\dfrac{1}{\sqrt{{a}^{2}+1}} $ ,
当 $ x-\varphi =2k\mathrm{\pi }+\dfrac{\mathrm{\pi }}{2} $ , $ k\in \boldsymbol{Z} $ 时,
$ \sqrt{{a}^{2}+1} \sin (x-\varphi ) $ 取到最大值 $ \sqrt{{a}^{2}+1} $ ,
可得 $ 2a\geqslant \sqrt{{a}^{2}+1} $ ,解得 $ a\geqslant \dfrac{\sqrt{3}}{3} $ ,当 $ x=2k\mathrm{\pi }+\dfrac{\mathrm{\pi }}{2}+\varphi $ , $ k\in \boldsymbol{Z} $ 时,等号成立.
所以实数 $ a $ 的取值范围是 $ [\dfrac{\sqrt{3}}{3},+\mathrm{\infty }) $ .
14.已知 $ f(x)=\dfrac{ \cos (2023\mathrm{\pi }-x) \cos (\dfrac{3\mathrm{\pi }}{2}-x) \sin (x+\dfrac{\mathrm{\pi }}{2})}{ \sin (-\mathrm{\pi }+x) \sin (x+3\mathrm{\pi }) \cos (\mathrm{\pi }+x)} $ .
(1) 化简函数 $ f(x) $ ;
(2) 若 $ f(\alpha )=\dfrac{1}{2} $ ,求 $ \sin \alpha \cos \alpha +2{ \sin }^{2}\alpha $ 的值;
(3) 若 $ f(\alpha -\beta )=-2 $ , $ f(\alpha )=-3 $ 且 $ \alpha \in (0,\dfrac{\mathrm{\pi }}{2}) $ , $ \beta \in (\dfrac{\mathrm{\pi }}{2},\mathrm{\pi }) $ ,求 $ 2\alpha -\beta $ 的值.
答案:(1) 【解】 $ f(x)= $
$ \dfrac{ \cos (2023\mathrm{\pi }-x) \cos (\dfrac{3\mathrm{\pi }}{2}-x) \sin (x+\dfrac{\mathrm{\pi }}{2})}{ \sin (-\mathrm{\pi }+x) \sin (x+3\mathrm{\pi }) \cos (\mathrm{\pi }+x)} $
$ =\dfrac{(- \cos x)(- \sin x)( \cos x)}{(- \sin x)(- \sin x)(- \cos x)} $
$ =-\dfrac{ \cos x}{ \sin x}=-\dfrac{1}{ \tan x} $ .
(2) 【解】由已知得, $ f(\alpha )=-\dfrac{1}{ \tan \alpha }=\dfrac{1}{2} $ ,
所以 $ \tan \alpha =-2 $ ,所以 $ \sin \alpha \cos \alpha +2{ \sin }^{2}\alpha =\dfrac{ \sin \alpha \cos \alpha +2{ \sin }^{2}\alpha }{{ \sin }^{2}\alpha +{ \cos }^{2}\alpha }=\dfrac{ \tan \alpha +2{ \tan }^{2}\alpha }{{ \tan }^{2}\alpha +1}=\dfrac{-2+8}{4+1}=\dfrac{6}{5} $ .
(3) 【解】由 $ f(\alpha -\beta )=-2 $ , $ f(\alpha )=-3 $ ,
可知 $ \tan (\alpha -\beta )=\dfrac{1}{2} $ , $ \tan \alpha =\dfrac{1}{3} $ ,
所以 $ \tan (2\alpha -\beta )= \tan [(\alpha -\beta )+\alpha ]=\dfrac{ \tan (\alpha -\beta )+ \tan \alpha }{1- \tan (\alpha -\beta ) \tan \alpha }=\dfrac{\dfrac{1}{2}+\dfrac{1}{3}}{1-\dfrac{1}{6}}=1 $ .
因为 $ \alpha \in (0,\dfrac{\mathrm{\pi }}{2}) $ , $ \beta \in (\dfrac{\mathrm{\pi }}{2},\mathrm{\pi }) $ ,
所以 $ -\mathrm{\pi } < \alpha -\beta < 0 $ ,且 $ \tan (\alpha -\beta )=\dfrac{1}{2} > 0 $ ,可得 $ -\mathrm{\pi } < \alpha -\beta < -\dfrac{\mathrm{\pi }}{2} $ ,所以 $ 2\alpha -\beta \in (-\mathrm{\pi },0) $ ,
所以 $ 2\alpha -\beta =-\dfrac{3\mathrm{\pi }}{4} $ .
解析:
15.如图,正方形 $ ABCD $ 的边长为 $ {\rm 1,} P $ , $ Q $ 分别为边 $ AB $ , $ AD $ 上的动点.
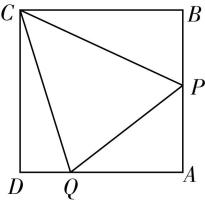
(1) 设 $ \mathrm{\angle }BCP=\alpha $ , $ \mathrm{\angle }DCQ=\beta $ ,请用含有 $ \alpha $ , $ \beta $ 的式子表示 $ △APQ $ 的周长 $ t $ ;
(2) 若点 $ P $ , $ Q $ 在运动的过程中, $ \mathrm{\angle }PCQ $ 的大小保持不变,试探究 $ △APQ $ 的周长 $ t $ 的变化情况.
答案:(1) 【解】由题知 $ BP= \tan \alpha $ , $ DQ= \tan \beta $ ,则 $ AP=1- \tan \alpha $ , $ AQ=1- \tan \beta $ ,
所以 $ △APQ $ 的周长 $ t=AP+AQ+PQ=2- \tan \alpha - \tan \beta +\sqrt{{\left(1- \tan \alpha \right) ^ {2}}+{\left(1- \tan \beta \right) ^ {2}}} $ .
(2) 【解】因为点 $ P $ , $ Q $ 在运动的过程中, $ \mathrm{\angle }PCQ $ 的大小保持不变,
所以 $ \alpha +\beta $ 的大小保持不变,所以 $ \tan (\alpha +\beta ) $ 为定值.
由(1)得 $ t=1- \tan \alpha +1- \tan \beta +\sqrt{{\left(1- \tan \alpha \right) ^ {2}}+{\left(1- \tan \beta \right) ^ {2}}} $ ,
令 $ x=1- \tan \alpha $ , $ y=1- \tan \beta $ ,
则有 $ t=x+y+\sqrt{{x}^{2}+{y}^{2}} $ ,化简得 $ 2t(x+y)={t}^{2}+2xy $ .
又 $ \tan (\alpha +\beta )=\dfrac{ \tan \alpha + \tan \beta }{1- \tan \alpha \tan \beta } $
$ =\dfrac{1-x+1-y}{1-(1-x)(1-y)}=\dfrac{2-(x+y)}{x+y-xy} $
$ =\dfrac{2-(x+y)}{x+y-t(x+y)+\dfrac{{t}^{2}}{2}}=\dfrac{-(x+y)+2}{(1-t)(x+y)+\dfrac{{t}^{2}}{2}} $ ,
要使得 $ \tan (\alpha +\beta ) $ 为定值,则有 $ \dfrac{-1}{2}=\dfrac{1-t}{\dfrac{{t}^{2}}{2}} $ ,
解得 $ t=2 $ ,
此时 $ \tan (\alpha +\beta )=1 $ , $ \alpha +\beta =\dfrac{\mathrm{\pi }}{4} $ ,即 $ \mathrm{\angle }PCQ=\dfrac{\mathrm{\pi }}{4} $ .
所以若点 $ P $ , $ Q $ 在运动的过程中, $ \mathrm{\angle }PCQ $ 的大小保持不变,
则 $ △APQ $ 的周长 $ t $ 为定值2.
解析:
16.在 $ △ABC $ 中, $ 3 \sin A+4 \cos B=6 $ , $ 3 \cos A+4 \sin B=1 $ ,则 $ C $ 的大小为( )
A. $ \dfrac{\mathrm{\pi }}{6} $
B. $ \dfrac{5}{6}\mathrm{\pi } $
C. $ \dfrac{\mathrm{\pi }}{6} $ 或 $ \dfrac{5}{6}\mathrm{\pi } $
D. $ \dfrac{\mathrm{\pi }}{3} $ 或 $ \dfrac{2}{3}\mathrm{\pi } $
答案:A
解析: $ \begin{cases}3 \sin A+4 \cos B=6,①\\ 3 \cos A+4 \sin B=1,②\end{cases} $
$ {①}^{2}+{②}^{2} $ ,得 $ 9+16+24 \sin (A+B)=37 $ ,
$ \therefore \sin (A+B)=\dfrac{1}{2} $ . $ \therefore $ 在 $ △ABC $ 中, $ \sin C=\dfrac{1}{2} $ , $ \therefore C=\dfrac{\mathrm{\pi }}{6} $ 或 $ C=\dfrac{5}{6}\mathrm{\pi } $ .
若 $ C=\dfrac{5}{6}\mathrm{\pi } $ ,则 $ A+B=\dfrac{\mathrm{\pi }}{6} $ .
$ \because 1-3 \cos A=4 \sin B > 0 $ , $ \therefore \cos A < \dfrac{1}{3} $ .
又 $ \because \dfrac{1}{3} < \dfrac{1}{2} $ , $ \therefore A > \dfrac{\mathrm{\pi }}{3} $ .
此时 $ A+C > \mathrm{\pi } $ ,不符合题意, $ \therefore C\ne \dfrac{5}{6}\mathrm{\pi } $ ,
$ \therefore C=\dfrac{\mathrm{\pi }}{6} $ .故选 $ \mathrm{A} $ .
17.已知 $ \sin (\mathrm{\pi }-\alpha )=\dfrac{4\sqrt{3}}{7} $ , $ \cos (\alpha -\beta )=\dfrac{13}{14} $ , $ 0 < \beta < \alpha < \dfrac{\mathrm{\pi }}{2} $ ,则角 $ \beta $ 的大小是 .
答案: $ \dfrac{\mathrm{\pi }}{3} $
解析:因为 $ \sin (\mathrm{\pi }-\alpha )=\dfrac{4\sqrt{3}}{7} $ ,所以 $ \sin \text{ }\alpha =\dfrac{4\sqrt{3}}{7} $ .
因为 $ 0 < \alpha < \dfrac{\mathrm{\pi }}{2} $ ,所以 $ \cos \text{ }\alpha =\sqrt{1-{ \sin }^{2}\alpha }=\dfrac{1}{7} $ .
因为 $ \cos (\alpha -\beta )=\dfrac{13}{14} $ ,且 $ 0 < \beta < \alpha < \dfrac{\mathrm{\pi }}{2} $ ,
所以 $ 0 < \alpha -\beta < \dfrac{\mathrm{\pi }}{2} $ ,
所以 $ \sin (\alpha -\beta )=\sqrt{1-{ \cos }^{2}(\alpha -\beta )}=\dfrac{3\sqrt{3}}{14} $ .
所以 $ \cos \text{ }\beta = \cos [\alpha -(\alpha -\beta )]= \cos \text{ }\alpha \cos (\alpha -\beta )+ \sin \text{ }\alpha \sin (\alpha -\beta )=\dfrac{1}{7}×\dfrac{13}{14}+\dfrac{4\sqrt{3}}{7}×\dfrac{3\sqrt{3}}{14}=\dfrac{1}{2} $ .
因为 $ 0 < \beta < \dfrac{\mathrm{\pi }}{2} $ ,所以 $ \beta =\dfrac{\mathrm{\pi }}{3} $ .
18.若0< $ {\rm \mathit{α}} $ < $ \dfrac{\mathrm{\pi }}{2} $ ,- $ \dfrac{\mathrm{\pi }}{2} $ < $ {\rm \mathit{β}} $ <0,cos $ (\dfrac{\mathrm{\pi }}{4}+\alpha ) $ = $ \dfrac{1}{3} $ ,cos $ (\dfrac{\mathrm{\pi }}{4}-\dfrac{\beta }{2}) $ = $ \dfrac{\sqrt{3}}{3} $ ,则cos $ (\alpha +\dfrac{\beta }{2}) $ = ( )
A. $ \dfrac{\sqrt{3}}{3} $
B.- $ \dfrac{\sqrt{3}}{3} $
C. $ \dfrac{5\sqrt{3}}{9} $
D.- $ \dfrac{\sqrt{6}}{9} $
答案:C
19.已知 $ 8 \cos (2\alpha +\beta )+5 \cos \text{ }\beta =0 $ ,且 $ \cos (\alpha +\beta )\cdot \cos \text{ }\alpha \ne 0 $ ,则 $ \tan (\alpha +\beta ) \tan \text{ }\alpha = $ .
解析: $ \because 8 \cos (2\alpha +\beta )+5 \cos \text{ }\beta =8[ \cos (\alpha +\beta ) \cos \text{ }\alpha - \sin (\alpha +\beta ) \sin \text{ }\alpha ]+5[ \cos (\alpha +\beta ) \cos \text{ }\alpha + \sin (\alpha +\beta ) \sin \text{ }\alpha ]=13 \cos (\alpha +\beta ) \cos \text{ }\alpha -3 \sin (\alpha +\beta ) \sin \text{ }\alpha =0 $ ,
$ \therefore 3 \sin (\alpha +\beta ) \sin \text{ }\alpha =13 \cos (\alpha +\beta ) \cos \text{ }\alpha $ ,
$ \therefore \tan (\alpha +\beta ) \tan \text{ }\alpha =\dfrac{13}{3} $ .



