5.6.1 匀速圆周运动的数学模型+5.6.2 函数y=Asin(wx+φ)的图象
一、刷基础
1.用“五点法”作函数 $ {\rm \mathit{y}=cos} (4x-\dfrac{\mathrm{\pi }}{6}) $ 在一个周期内的图象时,第四个关键点的坐标是 ( )
A. $ (\dfrac{5\mathrm{\pi }}{12},0) $
B. $ (-\dfrac{5\mathrm{\pi }}{12},1) $
C. $ (\dfrac{5\mathrm{\pi }}{12},1) $
D. $ (-\dfrac{5\mathrm{\pi }}{12},0) $
答案:A
解析:令 $ {\rm 4\mathit{x}-} \dfrac{\mathrm{\pi }}{6} {\rm =} $ $ \dfrac{3\mathrm{\pi }}{2} $ ,得 $ {\rm \mathit{x}=} \dfrac{5\mathrm{\pi }}{12} $ ,∴第四个关键点的坐标为 $ (\dfrac{5\mathrm{\pi }}{12},0) {\rm \mathit{.}} $ 故选A.
2.已知函数 $ f(x)=4 \sin (2x-\dfrac{\mathrm{\pi }}{6}) $ .
(1) 求 $ f(x) $ 的单调递减区间;
(2) 用“五点法”画出 $ f(x) $ 在一个周期内的图象.
答案:(1) 【解】令 $ 2k\mathrm{\pi }+\dfrac{\mathrm{\pi }}{2}\leqslant 2x-\dfrac{\mathrm{\pi }}{6}\leqslant 2k\mathrm{\pi }+\dfrac{3\mathrm{\pi }}{2}(k\in \boldsymbol{Z}) $ ,
解得 $ k\mathrm{\pi }+\dfrac{\mathrm{\pi }}{3}\leqslant x\leqslant k\mathrm{\pi }+\dfrac{5\mathrm{\pi }}{6}(k\in \boldsymbol{Z}) $ ,
则 $ f(x) $ 的单调递减区间是 $ [k\mathrm{\pi }+\dfrac{\mathrm{\pi }}{3} $ , $ k\mathrm{\pi }+\dfrac{5\mathrm{\pi }}{6} ] (k\in \boldsymbol{Z} ) $ .
(2)【解】
$ 2x-\dfrac{\mathrm{\pi }}{6} $ | 0 | $ \dfrac{\mathrm{\pi }}{2} $ | $ \mathrm{\pi } $ | $ \dfrac{3\mathrm{\pi }}{2} $ | $ 2\mathrm{\pi } $ |
$ x $ | $ \dfrac{\mathrm{\pi }}{12} $ | $ \dfrac{\mathrm{\pi }}{3} $ | $ \dfrac{7\mathrm{\pi }}{12} $ | $ \dfrac{5\mathrm{\pi }}{6} $ | $ \dfrac{13\mathrm{\pi }}{12} $ |
$ f(x) $ | 0 | 4 | 0 | $ -4 $ | 0 |
则 $ f(x) $ 在一个周期内的图象如图所示.

解析:
3.将函数 $ f(x)= \cos (3x+\dfrac{\mathrm{\pi }}{5}) $ 图象上所有的点向左平移 $ \dfrac{\mathrm{\pi }}{5} $ 个单位长度,得到函数 $ g(x) $ 的图象,则 $ g(x)= $ ( )
A. $ \cos (3x+\dfrac{2\mathrm{\pi }}{5}) $
B. $ \cos 3x $
C. $ - \sin (3x+\dfrac{3\mathrm{\pi }}{10}) $
D. $ \sin (3x+\dfrac{\mathrm{\pi }}{10}) $
答案:C
解析:由题意得 $ g(x)= \cos [3\cdot (x+\dfrac{\mathrm{\pi }}{5})+\dfrac{\mathrm{\pi }}{5}]= \cos (3x+\dfrac{4\mathrm{\pi }}{5})= \cos (3x+\dfrac{3\mathrm{\pi }}{10}+\dfrac{\mathrm{\pi }}{2})=- \sin (3x+\dfrac{3\mathrm{\pi }}{10}) $ .故选 $ \mathrm{C} $ .
4.将函数 $ f(x)= \sin (2x+\dfrac{\mathrm{\pi }}{3}) $ 的图象向左平移 $ \varphi (\varphi > 0) $ 个单位长度后,得到 $ y= \sin (2x+\dfrac{3\mathrm{\pi }}{4}) $ 的图象,则 $ \varphi $ 的最小值为 .
答案: $ \dfrac{5\mathrm{\pi }}{24} $
解析: $ f(x)= \sin (2x+\dfrac{\mathrm{\pi }}{3}) $ 的图象向左平移 $ \varphi (\varphi > 0) $ 个单位长度后,得到 $ y= \sin (2x+2\varphi +\dfrac{\mathrm{\pi }}{3}) $ 的图象,
从而 $ 2\varphi +\dfrac{\mathrm{\pi }}{3}=\dfrac{3\mathrm{\pi }}{4}+2k\mathrm{\pi } $ , $ k\in \boldsymbol{Z} $ ,解得 $ \varphi =\dfrac{5\mathrm{\pi }}{24}+k\mathrm{\pi } $ , $ k\in \boldsymbol{Z} $ ,又 $ \varphi > 0 $ ,故当 $ k=0 $ 时, $ \varphi $ 取得最小值,最小值为 $ \dfrac{5\mathrm{\pi }}{24} $ .
5.(多选)记函数 $ f(x)=3 \sin (x+\dfrac{\mathrm{\pi }}{5}) $ 的图象为 $ C $ ,为了得到函数 $ g(x)=3 \sin (2x-\dfrac{\mathrm{\pi }}{5}) $ 的图象,可能用到的变换方式有( )(多选)
A.将所有点的横坐标伸长到原来的2倍,纵坐标不变
B.将所有点的横坐标缩短到原来的 $ \dfrac{1}{2} $ ,纵坐标不变
C.将所有点向右平移 $ \dfrac{\mathrm{\pi }}{5} $ 个单位长度
D.将所有点向右平移 $ \dfrac{2\mathrm{\pi }}{5} $ 个单位长度
答案:BCD
解析:有两种变换方式,方式一:将图象 $ C $ 上所有的点向右平移 $ \dfrac{2\mathrm{\pi }}{5} $ 个单位长度,得到 $ y=3 \sin (x-\dfrac{2\mathrm{\pi }}{5}+\dfrac{\mathrm{\pi }}{5})=3 \sin (x-\dfrac{\mathrm{\pi }}{5}) $ 的图象,
再将 $ y=3 \sin (x-\dfrac{\mathrm{\pi }}{5}) $ 的图象上所有点的横坐标缩短到原来的 $ \dfrac{1}{2} $ ,纵坐标不变,得到 $ g(x)=3 \sin (2x-\dfrac{\mathrm{\pi }}{5}) $ 的图象.
方式二:将图象 $ C $ 上所有点的横坐标缩短到原来的 $ \dfrac{1}{2} $ ,纵坐标不变,得到 $ y=3 \sin (2x+\dfrac{\mathrm{\pi }}{5}) $ 的图象,
再将 $ y=3 \sin (2x+\dfrac{\mathrm{\pi }}{5}) $ 的图象上所有点向右平移 $ \dfrac{\mathrm{\pi }}{5} $ 个单位长度,得到 $ g(x)=3 \sin [2(x-\dfrac{\mathrm{\pi }}{5})+\dfrac{\mathrm{\pi }}{5}]=3 \sin (2x-\dfrac{\mathrm{\pi }}{5}) $ 的图象.
所以可能用到的变换方式有 $ \mathrm{B}\mathrm{C}\mathrm{D} $ ,没有 $ \mathrm{A} $ .故选 $ \mathrm{B}\mathrm{C}\mathrm{D} $ .
6.将函数 $ f(x)= \cos (2x+\dfrac{\mathrm{\pi }}{3}) $ 的图象向右平移 $ \dfrac{\mathrm{\pi }}{4} $ 个单位长度,再将所得图象的每个点的纵坐标变为原来的2倍,得到函数 $ g(x) $ 的图象,则 $ g(x)= $ ( )
A. $ 2 \cos (2x-\dfrac{\mathrm{\pi }}{6}) $
B. $ \dfrac{1}{2} \cos (2x-\dfrac{\mathrm{\pi }}{6}) $
C. $ 2 \cos (2x+\dfrac{\mathrm{\pi }}{12}) $
D. $ \dfrac{1}{2} \cos (2x+\dfrac{\mathrm{\pi }}{12}) $
答案:A
解析:将函数 $ f(x)= \cos (2x+\dfrac{\mathrm{\pi }}{3}) $ 的图象向右平移 $ \dfrac{\mathrm{\pi }}{4} $ 个单位长度,
可得函数 $ y= \cos [2(x-\dfrac{\mathrm{\pi }}{4})+\dfrac{\mathrm{\pi }}{3}]= \cos (2x-\dfrac{\mathrm{\pi }}{6}) $ 的图象,
将函数 $ y= \cos (2x-\dfrac{\mathrm{\pi }}{6}) $ 的图象的每个点的纵坐标变为原来的2倍,横坐标保持不变,
可得函数 $ y=2 \cos (2x-\dfrac{\mathrm{\pi }}{6}) $ 的图象,
所以 $ g(x)=2 \cos (2x-\dfrac{\mathrm{\pi }}{6}) $ .故选 $ \mathrm{A} $ .
7.将函数 $ f(x)= \sin 2x $ 的图象先向右平移 $ \dfrac{\mathrm{\pi }}{8} $ 个单位长度,再把所得函数图象的横坐标变为原来的 $ \dfrac{2}{\omega }(\omega > 0) $ 倍,纵坐标不变,得到函数 $ g(x) $ 的图象,若函数 $ g(x) $ 在 $ (\dfrac{\mathrm{\pi }}{4},\mathrm{\pi }) $ 上没有零点,则 $ \omega $ 的取值范围是 .
答案: $ (0,\dfrac{1}{4}]\cup [1,\dfrac{5}{4}] $
解析:将函数 $ f(x)= \sin 2x $ 的图象先向右平移 $ \dfrac{\mathrm{\pi }}{8} $ 个单位长度,得到函数 $ y= \sin 2(x-\dfrac{\mathrm{\pi }}{8})= \sin (2x-\dfrac{\mathrm{\pi }}{4}) $ 的图象,
再把所得函数图象的横坐标变为原来的 $ \dfrac{2}{\omega }(\omega > 0) $ 倍,纵坐标不变,得到函数 $ g(x)= \sin (2×\dfrac{\omega }{2}x-\dfrac{\mathrm{\pi }}{4})= \sin (\omega x-\dfrac{\mathrm{\pi }}{4}) $ 的图象.
当 $ x\in (\dfrac{\mathrm{\pi }}{4},\mathrm{\pi }) $ 时, $ \omega x-\dfrac{\mathrm{\pi }}{4}\in (\dfrac{\omega \mathrm{\pi }}{4}-\dfrac{\mathrm{\pi }}{4} $ , $ \omega \mathrm{\pi }-\dfrac{\mathrm{\pi }}{4}) $ .
由 $ g(x) $ 在 $ (\dfrac{\mathrm{\pi }}{4},\mathrm{\pi }) $ 上没有零点,得 $ \begin{cases}\dfrac{\omega \mathrm{\pi }}{4}-\dfrac{\mathrm{\pi }}{4}\geqslant k\mathrm{\pi },\\ \omega \mathrm{\pi }-\dfrac{\mathrm{\pi }}{4}\leqslant (k+1)\mathrm{\pi }\end{cases}(k\in \boldsymbol{Z}) $ ,
解得 $ 4k+1\leqslant \omega \leqslant k+\dfrac{5}{4}(k\in \boldsymbol{Z}) $ ,
又 $ 4k+1\leqslant k+\dfrac{5}{4}(k\in \boldsymbol{Z}) $ ,
且 $ \omega > 0 $ ,解得 $ 0 < \omega \leqslant \dfrac{1}{4} $ 或 $ 1\leqslant \omega \leqslant \dfrac{5}{4} $ .
8.函数 $ f (x )=a \sin x+b (x\in [0,2\mathrm{\pi } ] $ 且 $ a $ , $ b\in \boldsymbol{R}) $ 的图象如图所示,则函数 $ f(x) $ 的解析式为( )
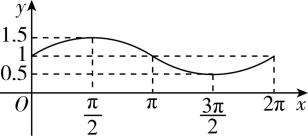
A. $ f(x)=\dfrac{1}{2} \sin x+1 $ , $ x\in [0,2\mathrm{\pi }] $
B. $ f(x)= \sin x+\dfrac{1}{2} $ , $ x\in [0,2\mathrm{\pi }] $
C. $ f(x)=\dfrac{3}{2} \sin x+1 $ , $ x\in [0,2\mathrm{\pi }] $
D. $ f(x)=\dfrac{3}{2} \sin x+\dfrac{1}{2} $ , $ x\in [0,2\mathrm{\pi }] $
答案:A
解析:把点 $ (0,1) $ 与点 $ (\dfrac{\mathrm{\pi }}{2},1.5) $ 的坐标代入 $ f(x)=a \sin x+b $ 中,可得 $ \begin{cases}b=1,\\ a+b=1.5,\end{cases} $ 解得 $ \begin{cases}a=0.5,\\ b=1,\end{cases} $ 因此 $ f(x)=\dfrac{1}{2} \sin x+1 $ , $ x\in [0,2\mathrm{\pi }] $ ,故选 $ \mathrm{A} $ .
9.已知函数 $ f (x )=A \sin (\omega x+\varphi ) (A > 0 $ , $ \omega > 0 $ , $ 0 < \varphi < \dfrac{\mathrm{\pi }}{2}) $ 的部分图象如图所示,则函数 $ f(x) $ 的解析式为( )

A. $ f(x)=\sqrt{2} \sin (x+\dfrac{\mathrm{\pi }}{3}) $
B. $ f(x)=2 \sin (x+\dfrac{\mathrm{\pi }}{3}) $
C. $ f(x)=\sqrt{2} \sin (2x+\dfrac{\mathrm{\pi }}{4}) $
D. $ f(x)=2 \sin (2x+\dfrac{\mathrm{\pi }}{6}) $
答案:D
解析:由图象可得, $ \dfrac{T}{4}=\dfrac{5\mathrm{\pi }}{12}-\dfrac{\mathrm{\pi }}{6}=\dfrac{\mathrm{\pi }}{4} $ ,故 $ T=\mathrm{\pi } $ ,则 $ |\omega |=\dfrac{2\mathrm{\pi }}{T}=2 $ ,又 $ \omega > 0 $ ,所以 $ \omega =2 $ .
又 $ f(\dfrac{5\mathrm{\pi }}{12})=A \sin (\dfrac{5\mathrm{\pi }}{6}+\varphi )=0 $ ,故 $ \dfrac{5\mathrm{\pi }}{6}+\varphi =k\mathrm{\pi } $ , $ k\in \boldsymbol{Z} $ ,
解得 $ \varphi =k\mathrm{\pi }-\dfrac{5\mathrm{\pi }}{6} $ , $ k\in \boldsymbol{Z} $ ,又 $ 0 < \varphi < \dfrac{\mathrm{\pi }}{2} $ ,所以 $ \varphi =\dfrac{\mathrm{\pi }}{6} $ ,
又 $ f(0)=A \sin \dfrac{\mathrm{\pi }}{6}=\dfrac{1}{2}A=1 $ ,故 $ A=2 $ ,
则 $ f(x)=2 \sin (2x+\dfrac{\mathrm{\pi }}{6}) $ .故选 $ \mathrm{D} $ .
10.将函数 $ f(x)= \sin (2x-\dfrac{\mathrm{\pi }}{6}) $ 的图象上所有点的横坐标变为原来的 $ \dfrac{1}{2} $ (纵坐标不变),得到函数 $ y=g(x) $ 的图象,则在下列区间中,函数 $ g(x) $ 单调递减的是( )
A. $ (0,\dfrac{\mathrm{\pi }}{8}) $
B. $ (\dfrac{\mathrm{\pi }}{8},\dfrac{\mathrm{\pi }}{4}) $
C. $ (\dfrac{\mathrm{\pi }}{4},\dfrac{3\mathrm{\pi }}{8}) $
D. $ (\dfrac{3\mathrm{\pi }}{8},\dfrac{\mathrm{\pi }}{2}) $
答案:C
解析:依题意可得, $ g(x)= \sin (4x-\dfrac{\mathrm{\pi }}{6}) $ ,
由 $ \dfrac{\mathrm{\pi }}{2}+2k\mathrm{\pi }\leqslant 4x-\dfrac{\mathrm{\pi }}{6}\leqslant \dfrac{3\mathrm{\pi }}{2}+2k\mathrm{\pi } $ , $ k\in \boldsymbol{Z} $ ,
解得 $ \dfrac{\mathrm{\pi }}{6}+\dfrac{k}{2}\mathrm{\pi }\leqslant x\leqslant \dfrac{5\mathrm{\pi }}{12}+\dfrac{k}{2}\mathrm{\pi } $ , $ k\in \boldsymbol{Z} $ .
观察选项可知,只需写出在 $ (0,\dfrac{\mathrm{\pi }}{2}) $ 上单调递减的区间即可.
易知当 $ k=0 $ 时, $ x\in (\dfrac{\mathrm{\pi }}{6},\dfrac{5\mathrm{\pi }}{12}) $ ,由选项可知只有 $ (\dfrac{\mathrm{\pi }}{4},\dfrac{3\mathrm{\pi }}{8} )\subseteq (\dfrac{\mathrm{\pi }}{6} $ , $ \dfrac{5\mathrm{\pi }}{12}) $ ,
可得在 $ (\dfrac{\mathrm{\pi }}{4},\dfrac{3\mathrm{\pi }}{8}) $ 上,函数 $ g(x) $ 单调递减.故选 $ \mathrm{C} $ .
11.若直线 $ x=-\dfrac{\mathrm{\pi }}{3} $ 是函数 $ f(x)= \cos x-b \sin x $ 图象的一条对称轴,则( )
A.函数 $ f(x) $ 的周期为 $ \mathrm{\pi } $
B.函数 $ f(x) $ 在 $ [-\dfrac{\mathrm{\pi }}{2},\dfrac{\mathrm{\pi }}{2}] $ 上的值域为 $ [-\dfrac{\sqrt{3}}{2},\dfrac{\sqrt{3}}{2}] $
C.函数 $ f(x) $ 在 $ (\mathrm{\pi },\dfrac{3\mathrm{\pi }}{2}) $ 上单调递增
D.将函数 $ f(x) $ 图象上的每一个点的纵坐标变为原来的 $ \dfrac{1}{2} $ ,再将所得到的图象向左平移 $ \dfrac{\mathrm{\pi }}{6} $ 个单位长度,可以得到 $ y= \sin x $ 的图象
答案:C
解析:因为直线 $ x=-\dfrac{\mathrm{\pi }}{3} $ 是函数 $ f(x)= \cos x-b \sin x $ 图象的一条对称轴,
所以 $ f(0)=f(-\dfrac{2\mathrm{\pi }}{3}) $ ,即 $ 1=-\dfrac{1}{2}+\dfrac{\sqrt{3}}{2}b $ ,解得 $ b=\sqrt{3} $ ,所以 $ f(x)= \cos x-\sqrt{3} \sin x=2 \cos (x+\dfrac{\mathrm{\pi }}{3}) $ ,则其周期为 $ 2\mathrm{\pi } $ ,故 $ \mathrm{A} $ 错误.
当 $ x\in [-\dfrac{\mathrm{\pi }}{2},\dfrac{\mathrm{\pi }}{2}] $ 时, $ x+\dfrac{\mathrm{\pi }}{3}\in [-\dfrac{\mathrm{\pi }}{6},\dfrac{5\mathrm{\pi }}{6}] $ ,则 $ \cos (x+\dfrac{\mathrm{\pi }}{3} )\in [-\dfrac{\sqrt{3}}{2} $ , $ 1 ] $ ,
所以 $ 2 \cos (x+\dfrac{\mathrm{\pi }}{3})\in [-\sqrt{3},2] $ ,
即函数 $ f(x) $ 在 $ [-\dfrac{\mathrm{\pi }}{2},\dfrac{\mathrm{\pi }}{2}] $ 上的值域为 $ [-\sqrt{3},2] $ ,故 $ \mathrm{B} $ 错误.
由 $ x+\dfrac{\mathrm{\pi }}{3}\in (-\mathrm{\pi }+2k\mathrm{\pi },2k\mathrm{\pi })(k\in \boldsymbol{Z}) $ ,得 $ x\in (-\dfrac{4\mathrm{\pi }}{3}+2k\mathrm{\pi } $ , $ -\dfrac{\mathrm{\pi }}{3}+2k\mathrm{\pi } ) (k\in \boldsymbol{Z} ) $ ,
则函数 $ f(x)=2 \cos (x+\dfrac{\mathrm{\pi }}{3}) $ 的单调递增区间为 $ (-\dfrac{4\mathrm{\pi }}{3}+2k\mathrm{\pi } $ , $ -\dfrac{\mathrm{\pi }}{3}+2k\mathrm{\pi } ) (k\in \boldsymbol{Z} ) $ .
因为 $ (\mathrm{\pi },\dfrac{3\mathrm{\pi }}{2} )\subseteq (-\dfrac{4\mathrm{\pi }}{3}+2k\mathrm{\pi } $ , $ -\dfrac{\mathrm{\pi }}{3}+2k\mathrm{\pi } ) (k\in \boldsymbol{Z} ) $ ,
所以函数 $ f(x) $ 在 $ (\mathrm{\pi },\dfrac{3\mathrm{\pi }}{2}) $ 上单调递增,故 $ \mathrm{C} $ 正确.
将函数 $ f(x)=2 \cos (x+\dfrac{\mathrm{\pi }}{3}) $ 图象上的每一个点的纵坐标变为原来的 $ \dfrac{1}{2} $ ,再将所得到的图象向左平移 $ \dfrac{\mathrm{\pi }}{6} $ 个单位长度,得到 $ y=\dfrac{1}{2}×2 \cos (x+\dfrac{\mathrm{\pi }}{6}+\dfrac{\mathrm{\pi }}{3})= \cos (x+\dfrac{\mathrm{\pi }}{2})=- \sin x $ 的图象,故 $ \mathrm{D} $ 错误.故选 $ \mathrm{C} $ .
12.把函数 $ y= \sin (2x+\dfrac{4\mathrm{\pi }}{3}) $ 的图象向右平移 $ \varphi (\varphi > 0) $ 个单位长度,所得图象关于 $ y $ 轴对称,则 $ \varphi $ 的最小值是( )
A. $ \dfrac{5\mathrm{\pi }}{6} $
B. $ \dfrac{2\mathrm{\pi }}{3} $
C. $ \dfrac{5\mathrm{\pi }}{12} $
D. $ \dfrac{\mathrm{\pi }}{6} $
答案:C
解析:将函数 $ y= \sin (2x+\dfrac{4\mathrm{\pi }}{3}) $ 的图象向右平移 $ \varphi (\varphi > 0) $ 个单位长度得到函数 $ y= \sin [2(x-\varphi )+\dfrac{4\mathrm{\pi }}{3}] $ 的图象,
$ \because $ 所得函数图象关于 $ y $ 轴对称,
即 $ \dfrac{4\mathrm{\pi }}{3}-2\varphi =\dfrac{\mathrm{\pi }}{2}+k\mathrm{\pi }(k\in \boldsymbol{Z}) $ ,
$ \therefore \varphi =\dfrac{5\mathrm{\pi }}{12}-\dfrac{k\mathrm{\pi }}{2}(k\in \boldsymbol{Z}) $ .
$ \because \varphi > 0 $ , $ \therefore $ 当 $ k=0 $ 时, $ \varphi $ 的最小值为 $ \dfrac{5\mathrm{\pi }}{12} $ .
故选 $ \mathrm{C} $ .
13.已知函数 $ f(x)=3 \cos (\omega x+\varphi )+2(\omega > 0,\left|\varphi \right| < \dfrac{\mathrm{\pi }}{2}) $ ,其图象与直线 $ y=5 $ 相邻两个交点的距离为 $ \dfrac{\mathrm{\pi }}{2} $ .若 $ \forall x\in [-\dfrac{\mathrm{\pi }}{12},\dfrac{\mathrm{\pi }}{16}] $ , $ f(x)\geqslant 2 $ 恒成立,则 $ \varphi $ 的取值范围是( )
A. $ [0,\dfrac{\mathrm{\pi }}{4}] $
B. $ [-\dfrac{\mathrm{\pi }}{4},-\dfrac{\mathrm{\pi }}{6}] $
C. $ [-\dfrac{\mathrm{\pi }}{3},\dfrac{\mathrm{\pi }}{6}] $
D. $ [-\dfrac{\mathrm{\pi }}{6},\dfrac{\mathrm{\pi }}{4}] $
答案:D
解析:由题意可知, $ f(x) $ 的最大值为 $ {\rm 5,} \because $ 函数 $ f(x)=3 \cos (\omega x+\varphi )+2(\omega > 0,\left|\varphi \right| < \dfrac{\mathrm{\pi }}{2}) $ ,其图象与直线 $ y=5 $ 相邻两个交点的距离为 $ \dfrac{\mathrm{\pi }}{2} $ , $ \therefore T=\dfrac{\mathrm{\pi }}{2} $ , $ \omega =\dfrac{2\mathrm{\pi }}{\dfrac{\mathrm{\pi }}{2}}=4 $ ,即 $ f(x)=3 \cos (4x+\varphi )+2 $ .
$ \because \forall x\in [-\dfrac{\mathrm{\pi }}{12},\dfrac{\mathrm{\pi }}{16}] $ , $ f(x)\geqslant 2 $ 恒成立,
$ \therefore \cos (4x+\varphi )\geqslant 0 $ .
$ \because x\in [-\dfrac{\mathrm{\pi }}{12},\dfrac{\mathrm{\pi }}{16}] $ , $ \therefore 4x+\varphi \in [-\dfrac{\mathrm{\pi }}{3}+\varphi ,\dfrac{\mathrm{\pi }}{4}+\varphi ].\text{ }\because \left|\varphi \right| < \dfrac{\mathrm{\pi }}{2} $ , $ \therefore -\dfrac{5\mathrm{\pi }}{6} < -\dfrac{\mathrm{\pi }}{3}+\varphi < \dfrac{\mathrm{\pi }}{6} $ , $ -\dfrac{\mathrm{\pi }}{4} < \dfrac{\mathrm{\pi }}{4}+\varphi < \dfrac{3\mathrm{\pi }}{4} $ , $ \therefore \begin{cases}-\dfrac{\mathrm{\pi }}{3}+\varphi \geqslant -\dfrac{\mathrm{\pi }}{2},\\ \dfrac{\mathrm{\pi }}{4}+\varphi \leqslant \dfrac{\mathrm{\pi }}{2},\end{cases} $
解得 $ -\dfrac{\mathrm{\pi }}{6}\leqslant \varphi \leqslant \dfrac{\mathrm{\pi }}{4} $ .
故选 $ \mathrm{D} $ .
14.(多选)已知函数 $ f(x)= \cos \omega x-\sqrt{3} \sin \omega x(\omega > 0) $ 的部分图象如图所示,则下列选项正确的是( )
 (多选)
(多选)
A.函数 $ f(x) $ 的图象关于点 $ (\dfrac{7\mathrm{\pi }}{12},0) $ 中心对称
B.函数 $ f(x) $ 的单调递增区间为 $ [k\mathrm{\pi }-\dfrac{2\mathrm{\pi }}{3} $ , $ k\mathrm{\pi }-\dfrac{\mathrm{\pi }}{6} ] (k\in \boldsymbol{Z} ) $
C.函数 $ f(x) $ 的图象可由 $ y=2 \sin \omega x $ 的图象向左平移 $ \dfrac{5\mathrm{\pi }}{6} $ 个单位长度得到
D.函数 $ g(x)=f(t\omega x)(t > 0) $ 在 $ (0,\mathrm{\pi }) $ 上有2个零点,则实数 $ t $ 的取值范围为 $ (\dfrac{7}{24},\dfrac{13}{24}] $
答案:ABD
解析:由题意, $ f(x)= \cos \omega x-\sqrt{3} \sin \omega x=-2 \sin (\omega x-\dfrac{\mathrm{\pi }}{6}) $ ,
由题图可知, $ \dfrac{3}{4}T=\dfrac{\mathrm{\pi }}{3}-(-\dfrac{5\mathrm{\pi }}{12})=\dfrac{3\mathrm{\pi }}{4} $ ,则 $ T=\mathrm{\pi }=\dfrac{2\mathrm{\pi }}{\omega } $ ,解得 $ \omega =2 $ ,所以 $ f(x)=-2 \sin (2x-\dfrac{\mathrm{\pi }}{6}) $ .
对于 $ \mathrm{A} $ , $ f(\dfrac{7\mathrm{\pi }}{12})=-2 \sin (2×\dfrac{7\mathrm{\pi }}{12}-\dfrac{\mathrm{\pi }}{6})=0 $ ,故 $ \mathrm{A} $ 正确;
对于 $ \mathrm{B} $ ,由 $ -\dfrac{3\mathrm{\pi }}{2}+2k\mathrm{\pi }\leqslant 2x-\dfrac{\mathrm{\pi }}{6}\leqslant -\dfrac{\mathrm{\pi }}{2}+2k\mathrm{\pi }(k\in \boldsymbol{Z}) $ ,解得 $ -\dfrac{2\mathrm{\pi }}{3}+k\mathrm{\pi }\leqslant x\leqslant -\dfrac{\mathrm{\pi }}{6}+k\mathrm{\pi }(k\in \boldsymbol{Z}) $ ,
所以函数 $ f(x)=-2 \sin (2x-\dfrac{\mathrm{\pi }}{6}) $ 的单调递增区间为 $ [k\mathrm{\pi }-\dfrac{2\mathrm{\pi }}{3} $ , $ k\mathrm{\pi }-\dfrac{\mathrm{\pi }}{6} ] (k\in \boldsymbol{Z} ) $ ,故 $ \mathrm{B} $ 正确;
对于 $ \mathrm{C} $ ,函数 $ y=2 \sin 2x $ 的图象向左平移 $ \dfrac{5\mathrm{\pi }}{6} $ 个单位长度得到 $ y=2 \sin [2(x+\dfrac{5\mathrm{\pi }}{6})]=2 \sin (2x+\dfrac{5\mathrm{\pi }}{3}) $ 的图象,
又 $ 2 \sin (2x+\dfrac{5\mathrm{\pi }}{3})=2 \sin (2\mathrm{\pi }+2x-\dfrac{\mathrm{\pi }}{3})=2 \sin (2x-\dfrac{\mathrm{\pi }}{3}) $ ,故 $ \mathrm{C} $ 错误;
对于 $ \mathrm{D} $ , $ g(x)=f(2tx)=-2 \sin (4tx-\dfrac{\mathrm{\pi }}{6}) $ ,
当 $ x\in (0,\mathrm{\pi }) $ 时, $ 4tx-\dfrac{\mathrm{\pi }}{6}\in (-\dfrac{\mathrm{\pi }}{6} $ , $ 4t\mathrm{\pi }-\dfrac{\mathrm{\pi }}{6}) $ ,又 $ g(x) $ 有两个零点,作出 $ y=-2 \sin x $ 的图象如图所示,则 $ 4t\mathrm{\pi }-\dfrac{\mathrm{\pi }}{6}\in (\mathrm{\pi },2\mathrm{\pi }] $ ,解得 $ t\in (\dfrac{7}{24},\dfrac{13}{24}] $ ,故 $ \mathrm{D} $ 正确.
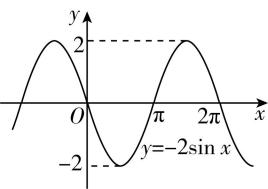
故选 $ \mathrm{A}\mathrm{B}\mathrm{D} $ .
15.已知函数 $ f(x)= \sin (\omega x+\varphi ) $ ,如图, $ A $ , $ B $ 是直线 $ y=\dfrac{1}{2} $ 与曲线 $ y=f(x) $ 的两个交点.若 $ |AB|=\dfrac{\mathrm{\pi }}{6} $ ,则 $ f(\mathrm{\pi })= $ .
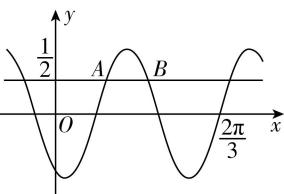
答案: $ -\dfrac{\sqrt{3}}{2} $
解析:设 $ A({x}_{1},\dfrac{1}{2}) $ , $ B({x}_{2},\dfrac{1}{2}) $ ,由 $ |AB|=\dfrac{\mathrm{\pi }}{6} $ 可得 $ {x}_{2}-{x}_{1}=\dfrac{\mathrm{\pi }}{6} $ ,
由 $ \sin x=\dfrac{1}{2} $ 可得 $ x=\dfrac{\mathrm{\pi }}{6}+2k\mathrm{\pi } $ 或 $ x=\dfrac{5\mathrm{\pi }}{6}+2k\mathrm{\pi } $ , $ k\in \boldsymbol{Z} $ ,
由图可知, $ \omega {x}_{2}+\varphi -(\omega {x}_{1}+\varphi )=\dfrac{5\mathrm{\pi }}{6}-\dfrac{\mathrm{\pi }}{6}=\dfrac{2\mathrm{\pi }}{3} $ ,即 $ \omega ({x}_{2}-{x}_{1})=\dfrac{2\mathrm{\pi }}{3} $ ,解得 $ \omega =4 $ .
因为 $ f(\dfrac{2\mathrm{\pi }}{3})= \sin (\dfrac{8\mathrm{\pi }}{3}+\varphi )=0 $ ,所以 $ \dfrac{8\mathrm{\pi }}{3}+\varphi =k\mathrm{\pi } $ , $ k\in \boldsymbol{Z} $ ,即 $ \varphi =-\dfrac{8\mathrm{\pi }}{3}+k\mathrm{\pi } $ , $ k\in \boldsymbol{Z} $ ,
所以, $ k\in \boldsymbol{Z} $ ,
所以 $ f(x)= \sin (4x-\dfrac{2\mathrm{\pi }}{3}) $ 或 $ f(x)=- \sin (4x-\dfrac{2\mathrm{\pi }}{3}) $ ,
又因为 $ f(0) < 0 $ ,所以 $ f(x)= \sin (4x-\dfrac{2\mathrm{\pi }}{3}) $ ,所以 $ f(\mathrm{\pi })= \sin (4\mathrm{\pi }-\dfrac{2}{3}\mathrm{\pi })=-\dfrac{\sqrt{3}}{2} $ .
16.已知函数 $ f(x)=A \sin (\omega x+\varphi )+B(A > 0,\omega > 0,0 < \varphi < \mathrm{\pi }) $ 的图象如图所示.
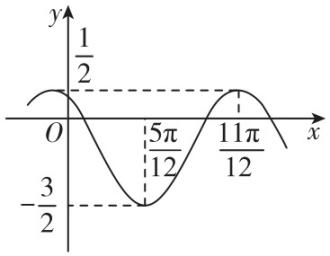
(1) 求函数 $ f(x) $ 的解析式;
(2) 将函数 $ f(x) $ 的图象上所有点的横坐标缩短为原来的 $ \dfrac{1}{2} $ ,再向右平移 $ \dfrac{\mathrm{\pi }}{3} $ 个单位长度,得到函数 $ y=g(x) $ 的图象,若 $ x\in [-\dfrac{\mathrm{\pi }}{24},\dfrac{\mathrm{\pi }}{4}] $ ,求函数 $ g(x) $ 的值域.
答案:(1) 【解】由题图知,函数 $ f(x) $ 的最大值为 $ \dfrac{1}{2} $ ,最小值为 $ -\dfrac{3}{2} $ ,
则 $ A+B=\dfrac{1}{2} $ , $ -A+B=-\dfrac{3}{2} $ ,
所以 $ A=1 $ , $ B=-\dfrac{1}{2} $ ,
所以 $ f(x)= \sin (\omega x+\varphi )-\dfrac{1}{2} $ .
因为函数 $ f(x) $ 图象的相邻两条对称轴之间的距离为 $ \dfrac{\mathrm{\pi }}{2} $ ,
所以 $ T=\mathrm{\pi } $ ,可得 $ \dfrac{2\mathrm{\pi }}{\omega }=\mathrm{\pi }⇒\omega =2 $ .
由题图知,当 $ x=\dfrac{5\mathrm{\pi }}{12} $ 时, $ f(x) $ 取得最小值,
所以 $ 2×\dfrac{5\mathrm{\pi }}{12}+\varphi =2k\mathrm{\pi }+\dfrac{3\mathrm{\pi }}{2}(k\in \boldsymbol{Z}) $ ,解得 $ \varphi =2k\mathrm{\pi }+\dfrac{2\mathrm{\pi }}{3}(k\in \boldsymbol{Z}) $ ,
又 $ 0 < \varphi < \mathrm{\pi } $ ,所以 $ \varphi =\dfrac{2\mathrm{\pi }}{3} $ ,
所以 $ f(x)= \sin (2x+\dfrac{2\mathrm{\pi }}{3})-\dfrac{1}{2} $ .
(2) 【解】将函数 $ f(x) $ 的图象上所有点的横坐标缩短为原来的 $ \dfrac{1}{2} $ ,可得 $ y= \sin (4x+\dfrac{2\mathrm{\pi }}{3})-\dfrac{1}{2} $ 的图象,
再向右平移 $ \dfrac{\mathrm{\pi }}{3} $ 个单位长度,可得 $ g(x)= \sin [4(x-\dfrac{\mathrm{\pi }}{3})+\dfrac{2\mathrm{\pi }}{3}]-\dfrac{1}{2}= \sin (4x-\dfrac{2\mathrm{\pi }}{3})-\dfrac{1}{2} $ 的图象.
当 $ x\in [-\dfrac{\mathrm{\pi }}{24},\dfrac{\mathrm{\pi }}{4}] $ 时, $ 4x-\dfrac{2\mathrm{\pi }}{3}\in [-\dfrac{5\mathrm{\pi }}{6} $ , $ \dfrac{\mathrm{\pi }}{3} ] $ ,
当 $ 4x-\dfrac{2\mathrm{\pi }}{3}=-\dfrac{\mathrm{\pi }}{2} $ ,即 $ x=\dfrac{\mathrm{\pi }}{24} $ 时,函数 $ g(x) $ 取得最小值,最小值为 $ -\dfrac{3}{2} $ ,
当 $ 4x-\dfrac{2\mathrm{\pi }}{3}=\dfrac{\mathrm{\pi }}{3} $ ,即 $ x=\dfrac{\mathrm{\pi }}{4} $ 时,函数 $ g(x) $ 取得最大值,最大值为 $ \dfrac{\sqrt{3}-1}{2} $ ,
故函数 $ g(x) $ 的值域为 $ [-\dfrac{3}{2} $ , $ \dfrac{\sqrt{3}-1}{2} ] $ .
解析:
17.先使函数 $ y=f(x) $ 图象上每一点的纵坐标保持不变,横坐标缩短为原来的 $ \dfrac{1}{2} $ ,然后将所得图象沿 $ x $ 轴向左平移 $ \dfrac{\mathrm{\pi }}{6} $ 个单位长度得到的函数图象与 $ y= \sin \text{ }2x $ 的图象相同,则 $ f(x) $ 的表达式为( )
A. $ f(x)= \sin (4x-\dfrac{\mathrm{\pi }}{3}) $
B. $ f(x)= \sin (x-\dfrac{\mathrm{\pi }}{6}) $
C. $ f(x)= \sin (4x+\dfrac{\mathrm{\pi }}{3}) $
D. $ f(x)= \sin (x-\dfrac{\mathrm{\pi }}{3}) $
答案:D
解析:方法一:正向变换
$ y=f(x) $ 的图象 $ {\xrightarrow[ ~\text{纵坐标不变}]{\text{横坐标缩短为原来的}\dfrac{1}{2}}} y=f\left(2x\right) $ 的图象 $ {\xrightarrow[ \dfrac{\mathrm{\pi~}}{6}\text{个单位长度}]{\text{沿}x\text{轴向左平移}}} y=f\left(2\left(x+\dfrac{\mathrm{\pi }}{6}\right)\right) $ ,即 $ y=f(2x+\dfrac{\mathrm{\pi }}{3}) $ 的图象,所以 $ f(2x+\dfrac{\mathrm{\pi }}{3})= \sin \text{ }2x $ .
令 $ 2x+\dfrac{\mathrm{\pi }}{3}=t $ ,则 $ 2x=t-\dfrac{\mathrm{\pi }}{3} $ ,
所以 $ f(t)= \sin (t-\dfrac{\mathrm{\pi }}{3}) $ ,
即 $ f(x)= \sin (x-\dfrac{\mathrm{\pi }}{3}) $ .故选 $ \mathrm{D} $ .
方法二:逆向变换
$ y= \sin \text{ }2x $ 的图象 $ {\xrightarrow[ \dfrac{\mathrm{\pi~}}{6}\text{个单位长度}]{\text{沿}x\text{轴向右平移}}} y= \sin \left[2\left(x-\dfrac{\mathrm{\pi }}{6}\right)\right]= \sin \left(2x-\dfrac{\mathrm{\pi }}{3}\right) $ 的图象 $ {\xrightarrow[ ~\text{纵坐标不变}]{\text{横坐标伸长到原来的}2\text{倍}}} y= \sin \left(x-\dfrac{\mathrm{\pi }}{3}\right)=f\left(x\right) $ 的图象.故选 $ \mathrm{D} $ .
18.为了得到函数 $ y= \sin (2x+\dfrac{\mathrm{\pi }}{3}) $ 的图象,只需把函数 $ y= \cos 2x $ 图象上所有的点( )
A.向左平移 $ \dfrac{\mathrm{\pi }}{3} $ 个单位长度
B.向右平移 $ \dfrac{\mathrm{\pi }}{3} $ 个单位长度
C.向左平移 $ \dfrac{\mathrm{\pi }}{12} $ 个单位长度
D.向右平移 $ \dfrac{\mathrm{\pi }}{12} $ 个单位长度
答案:D
解析:易知 $ y= \cos 2x= \sin (2x+\dfrac{\mathrm{\pi }}{2}) $ ,
又因为 $ \sin (2x+\dfrac{\mathrm{\pi }}{3})= \sin (2x-\dfrac{\mathrm{\pi }}{6}+\dfrac{\mathrm{\pi }}{2})= \sin [2(x-\dfrac{\mathrm{\pi }}{12})+\dfrac{\mathrm{\pi }}{2}] $ ,
因此只需将 $ y= \cos 2x= \sin (2x+\dfrac{\mathrm{\pi }}{2}) $ 图象上所有的点向右平移 $ \dfrac{\mathrm{\pi }}{12} $ 个单位长度即可.故选 $ \mathrm{D} $ .
19.函数 $ y=3 \sin (\omega x+\varphi )(\omega > 0,\varphi \in [0,2\mathrm{\pi })) $ 的部分图象如图所示,试求函数 $ y=3 \sin (\omega x+\varphi ) $ 的表达式.
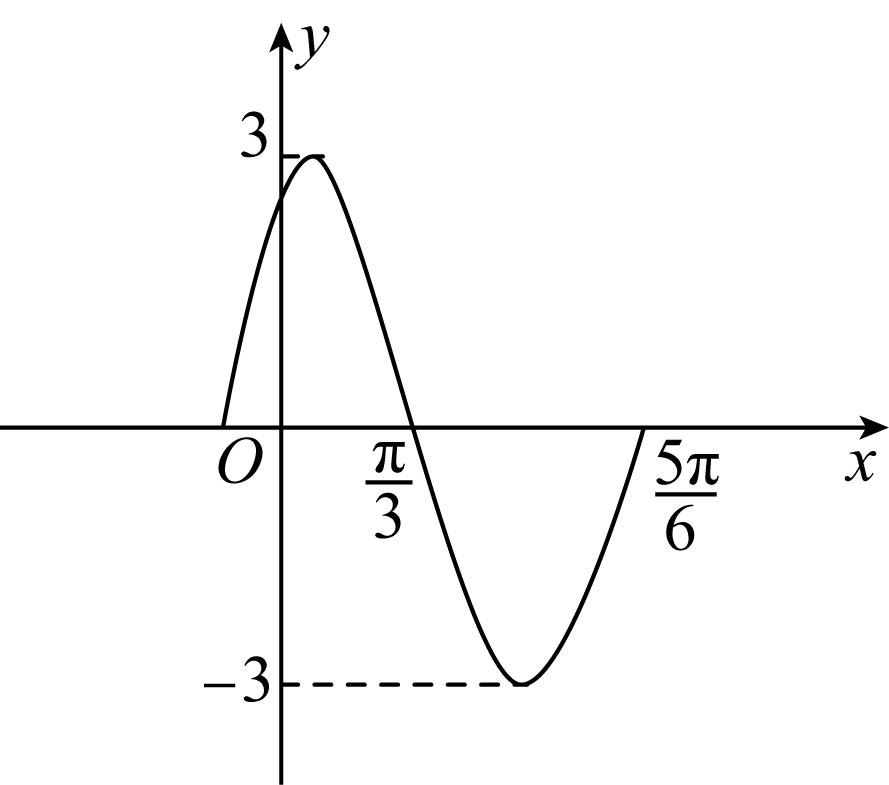
解析:由题图知,函数的最小正周期 $ T=2(\dfrac{5\mathrm{\pi }}{6}-\dfrac{\mathrm{\pi }}{3})=\mathrm{\pi } $ ,所以 $ \omega =\dfrac{2\mathrm{\pi }}{T}=2 $ ,所以 $ y=3 \sin (2x+\varphi ) $ .
又图象过点 $ (\dfrac{\mathrm{\pi }}{3},0) $ ,所以当 $ x=\dfrac{\mathrm{\pi }}{3} $ 时, $ y=0 $ ,由“五点法”作图得 $ 2×\dfrac{\mathrm{\pi }}{3}+\varphi =2k\mathrm{\pi }+\mathrm{\pi }(k\in \mathrm{Z}) $ ,由 $ \varphi \in [0,2\mathrm{\pi }) $ ,解得 $ \varphi =\dfrac{\mathrm{\pi }}{3} $ ,故所求函数的表达式为 $ y=3 \sin (2x+\dfrac{\mathrm{\pi }}{3}) $ .



 (多选)
(多选)


