第5.6节综合训练
一、刷能力
1.要得到函数 $ f(x)= \sin (2x-\dfrac{\mathrm{\pi }}{6}) $ 的图象,可以将函数 $ g(x)= \cos (2x-\dfrac{\mathrm{\pi }}{3}) $ 的图象( )
A.向右平移 $ \dfrac{\mathrm{\pi }}{6} $ 个单位长度
B.向左平移 $ \dfrac{\mathrm{\pi }}{6} $ 个单位长度
C.向右平移 $ \dfrac{\mathrm{\pi }}{3} $ 个单位长度
D.向左平移 $ \dfrac{\mathrm{\pi }}{3} $ 个单位长度
答案:A
解析:因为 $ g(x)= \cos (2x-\dfrac{\mathrm{\pi }}{3})= \sin (2x-\dfrac{\mathrm{\pi }}{3}+\dfrac{\mathrm{\pi }}{2})= \sin (2x+\dfrac{\mathrm{\pi }}{6}) $ ,
且 $ f(x)= \sin (2x-\dfrac{\mathrm{\pi }}{6})= \sin (2x+\dfrac{\mathrm{\pi }}{6}-\dfrac{\mathrm{\pi }}{3})= \sin [2(x-\dfrac{\mathrm{\pi }}{6})+\dfrac{\mathrm{\pi }}{6}] $ ,
所以将函数 $ g(x) $ 的图象向右平移 $ \dfrac{\mathrm{\pi }}{6} $ 个单位长度得到函数 $ f(x) $ 的图象.故选 $ \mathrm{A} $ .
2.将函数 $ f(x)= \sin x(x\in \boldsymbol{R}) $ 的图象上所有的点向左平移 $ \dfrac{\mathrm{\pi }}{3} $ 个单位长度,再将图象上所有点的横坐标伸长到原来的2倍(纵坐标不变),然后将图象上所有点的纵坐标伸长到原来的2倍(横坐标不变),则所得图象对应的函数解析式为( )
A. $ y=2 \sin (2x+\dfrac{\mathrm{\pi }}{3}) $ , $ x\in \boldsymbol{R} $
B. $ y=2 \sin (\dfrac{x}{2}+\dfrac{\mathrm{\pi }}{3}) $ , $ x\in \boldsymbol{R} $
C. $ y=2 \sin (\dfrac{x}{2}+\dfrac{\mathrm{\pi }}{6}) $ , $ x\in \boldsymbol{R} $
D. $ y=\dfrac{1}{2} \sin (2x+\dfrac{2\mathrm{\pi }}{3}) $ , $ x\in \boldsymbol{R} $
答案:B
解析:将函数 $ f(x)= \sin x(x\in \boldsymbol{R}) $ 的图象上所有的点向左平移 $ \dfrac{\mathrm{\pi }}{3} $ 个单位长度得到 $ y= \sin (x+\dfrac{\mathrm{\pi }}{3}) $ 的图象,
再将图象上所有点的横坐标伸长到原来的2倍(纵坐标不变)得到 $ y= \sin (\dfrac{x}{2}+\dfrac{\mathrm{\pi }}{3}) $ 的图象,
然后将图象上所有点的纵坐标伸长到原来的2倍(横坐标不变),则所得图象对应的函数解析式为 $ y=2 \sin (\dfrac{x}{2}+\dfrac{\mathrm{\pi }}{3}) $ , $ x\in \boldsymbol{R} $ ,故选 $ \mathrm{B} $ .
3.已知函数 $ f(x)=A \cos (\omega x+\varphi )(A > 0,\omega > 0,|\varphi | < \dfrac{\mathrm{\pi }}{2}) $ 的部分图象如图所示,将函数 $ f(x) $ 的图象向右平移 $ \dfrac{\mathrm{\pi }}{4} $ 个单位长度得到函数 $ g(x) $ 的图象,则( )

A. $ g(x)=2 \sin (x-\dfrac{\mathrm{\pi }}{3}) $
B. $ g(x)=2 \sin (2x+\dfrac{\mathrm{\pi }}{3}) $
C. $ g(x)=2 \cos (x-\dfrac{\mathrm{\pi }}{3}) $
D. $ g(x)=2 \cos (2x+\dfrac{\mathrm{\pi }}{3}) $
答案:B
解析:由题图知 $ A=2 $ , $ T=\dfrac{2\mathrm{\pi }}{\omega }=4×(\dfrac{7\mathrm{\pi }}{12}-\dfrac{\mathrm{\pi }}{3})=\mathrm{\pi } $ ,所以 $ \omega =2 $ ,
再根据五点作图法可得 $ 2×\dfrac{7\mathrm{\pi }}{12}+\varphi =\dfrac{3\mathrm{\pi }}{2} $ ,解得 $ \varphi =\dfrac{\mathrm{\pi }}{3} $ ,
所以 $ f(x)=2 \cos (2x+\dfrac{\mathrm{\pi }}{3}) $ .
将函数 $ f(x) $ 的图象向右平移 $ \dfrac{\mathrm{\pi }}{4} $ 个单位长度得到 $ g(x)=2 \cos [2(x-\dfrac{\mathrm{\pi }}{4})+\dfrac{\mathrm{\pi }}{3}]=2 \sin (2x+\dfrac{\mathrm{\pi }}{3}) $ 的图象.故选 $ \mathrm{B} $ .
4.已知函数 $ {\rm \mathit{f}(\mathit{x})=sin} (\omega x+\dfrac{\mathrm{\pi }}{3}) $ (0< $ {\rm \mathit{ω}} $ <3),将f(x)的图象向左平移 $ \dfrac{\mathrm{\pi }}{2} $ 个单位长度后得到函数g(x)的图象,若g(x)与f(x)的图象关于原点对称,则 $ {\rm \mathit{ω}} $ 的值为 ( )
A.1
B. $ \dfrac{4}{3} $
C.2
D. $ \dfrac{8}{3} $
答案:D
解析:因为将函数 $ {\rm \mathit{f}(\mathit{x})=sin} (\omega x+\dfrac{\mathrm{\pi }}{3}) $ 的图象向左平移 $ \dfrac{\mathrm{\pi }}{2} $ 个单位长度后得到函数g(x)的图象,所以 $ {\rm \mathit{g}(\mathit{x})=sin} (\omega x+\dfrac{\mathrm{\pi }}{2}\omega +\dfrac{\mathrm{\pi }}{3}) {\rm \mathit{.}} $
因为g(x)与f(x)的图象关于原点对称,函数f(x)的图象关于原点对称的图象对应的函数解析式为 $ {\rm \mathit{y}=-sin} (-\omega x+\dfrac{\mathrm{\pi }}{3}) $ ,
所以 $ {\rm -sin} (-\omega x+\dfrac{\mathrm{\pi }}{3}) {\rm =sin} $ 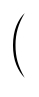 $ {\rm \mathit{ωx}+} \dfrac{\mathrm{\pi }}{2} {\rm \mathit{ω}+} $ $ \dfrac{\mathrm{\pi }}{3} $
$ {\rm \mathit{ωx}+} \dfrac{\mathrm{\pi }}{2} {\rm \mathit{ω}+} $ $ \dfrac{\mathrm{\pi }}{3} $  ,即 $ {\rm sin} (\omega x-\dfrac{\mathrm{\pi }}{3}) {\rm =sin} $
,即 $ {\rm sin} (\omega x-\dfrac{\mathrm{\pi }}{3}) {\rm =sin} $ 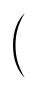 $ {\rm \mathit{ωx}+} \dfrac{\mathrm{\pi }}{2} {\rm \mathit{ω}+} $ $ \dfrac{\mathrm{\pi }}{3} $
$ {\rm \mathit{ωx}+} \dfrac{\mathrm{\pi }}{2} {\rm \mathit{ω}+} $ $ \dfrac{\mathrm{\pi }}{3} $ 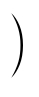 ,
,
所以 $ \dfrac{\mathrm{\pi }}{2} {\rm \mathit{ω}+} $ $ \dfrac{\mathrm{\pi }}{3} {\rm +} $ $ \dfrac{\mathrm{\pi }}{3} {\rm =2\mathit{k}π,\mathit{k}∈Z} $ ,所以 $ {\rm \mathit{ω}=4\mathit{k}-} \dfrac{4}{3} {\rm ,\mathit{k}∈Z\mathit{.}} $
又0< $ {\rm \mathit{ω}} $ <3,所以 $ {\rm \mathit{ω}=4-} \dfrac{4}{3} {\rm =} $ $ \dfrac{8}{3} {\rm \mathit{.}} $ 故选D.
5.函数 $ f(x) $ 的图象是由 $ y= \sin x $ 的图象向右平移 $ \dfrac{\mathrm{\pi }}{6} $ 个单位长度,再将图象上所有点的横坐标变为原来的 $ \dfrac{1}{\omega }(\omega > 0) $ 倍(纵坐标不变)得到的,若函数 $ f(x) $ 在区间 $ [0,\mathrm{\pi }] $ 上有且仅有两个零点,则 $ \omega $ 的取值范围是( )
A. $ [\dfrac{7}{6},\dfrac{13}{6}) $
B. $ [\dfrac{5}{6},\dfrac{11}{6}] $
C. $ [\dfrac{7}{6},\dfrac{13}{6}] $
D. $ [\dfrac{5}{6},\dfrac{11}{6}) $
答案:A
解析:将函数 $ y= \sin x $ 的图象向右平移 $ \dfrac{\mathrm{\pi }}{6} $ 个单位长度,可得 $ y= \sin (x-\dfrac{\mathrm{\pi }}{6}) $ 的图象,
再将图象上每个点的横坐标变为原来的 $ \dfrac{1}{\omega }(\omega > 0) $ 倍(纵坐标不变),
得到函数 $ y=f(x)= \sin (\omega x-\dfrac{\mathrm{\pi }}{6}) $ 的图象.
因为函数 $ y=f(x) $ 在区间 $ [0,\mathrm{\pi }] $ 上有且仅有两个零点, $ \omega \cdot 0-\dfrac{\mathrm{\pi }}{6}=-\dfrac{\mathrm{\pi }}{6} $ ,
所以 $ \omega \cdot \mathrm{\pi }-\dfrac{\mathrm{\pi }}{6}\in [\mathrm{\pi },2\mathrm{\pi }) $ ,
所以 $ \omega \in [\dfrac{7}{6},\dfrac{13}{6}) $ .故选 $ \mathrm{A} $ .
6.已知 $ f(x)={ \sin }^{2}(\omega x+\dfrac{\mathrm{\pi }}{3})-{ \cos }^{2}(\omega x+\dfrac{\mathrm{\pi }}{3})(\omega > 0) $ .给出下列判断:
①若 $ f({x}_{1})=1 $ , $ f({x}_{2})=-1 $ ,且 $ {\left|{x}_{1}-{x}_{2}\right|}_{ \min }=\dfrac{\mathrm{\pi }}{2} $ ,则 $ \omega =2 $ ;
②若 $ f(x) $ 在 $ [0,2\mathrm{\pi }] $ 上恰有9个零点,则 $ \omega $ 的取值范围为 $ [\dfrac{53}{24},\dfrac{59}{24}) $ ;
③存在 $ \omega \in (0,2) $ ,使得 $ f(x) $ 的图象向右平移 $ \dfrac{\mathrm{\pi }}{6} $ 个单位长度后得到的图象关于 $ y $ 轴对称;
④若 $ f(x) $ 在 $ [-\dfrac{\mathrm{\pi }}{6},\dfrac{\mathrm{\pi }}{3}] $ 上单调递增,则 $ \omega $ 的取值范围为 $ (0,\dfrac{1}{3}] $ .
其中,判断正确的个数为( )
A.1
B.2
C.3
D.4
答案:A
解析:依题意得 $ f(x)=- \cos (2\omega x+\dfrac{2\mathrm{\pi }}{3}) $ , $ \omega > 0 $ .
对于①,由题意得 $ T=\mathrm{\pi } $ , $ T=\dfrac{2\mathrm{\pi }}{2\omega }=\mathrm{\pi }⇒\omega =1 $ ,故①错误;
对于②,由题意得 $ x\in [0,2\mathrm{\pi }] $ ,则 $ \dfrac{2\mathrm{\pi }}{3}\leqslant 2\omega x+\dfrac{2\mathrm{\pi }}{3}\leqslant 4\omega \mathrm{\pi }+\dfrac{2\mathrm{\pi }}{3} $ ,若 $ f(x) $ 在 $ [0,2\mathrm{\pi }] $ 上恰有9个零点,则 $ \dfrac{19\mathrm{\pi }}{2}\leqslant 4\omega \mathrm{\pi }+\dfrac{2\mathrm{\pi }}{3} < \dfrac{21\mathrm{\pi }}{2} $ ,得 $ \dfrac{53}{24}\leqslant \omega < \dfrac{59}{24} $ ,故②正确;
对于③,由题意得 $ f(x) $ 的图象向右平移 $ \dfrac{\mathrm{\pi }}{6} $ 个单位长度后,得到的图象所对应的函数解析式为 $ g(x)=- \cos (2\omega x-\dfrac{\mathrm{\pi }\omega }{3}+\dfrac{2\mathrm{\pi }}{3}) $ ,又 $ \omega \in (0,2) $ ,所以 $ 0 < -\dfrac{\mathrm{\pi }\omega }{3}+\dfrac{2\mathrm{\pi }}{3} < \dfrac{2\mathrm{\pi }}{3} $ ,不能得出 $ g(x) $ 的图象关于 $ y $ 轴对称,故③错误;
对于④,当 $ x\in [-\dfrac{\mathrm{\pi }}{6},\dfrac{\mathrm{\pi }}{3}] $ 时, $ -\dfrac{\mathrm{\pi }\omega }{3}+\dfrac{2\mathrm{\pi }}{3}\leqslant 2\omega x+\dfrac{2\mathrm{\pi }}{3}\leqslant \dfrac{2\mathrm{\pi }\omega }{3}+\dfrac{2\mathrm{\pi }}{3} $ ,若 $ f(x) $ 在 $ [-\dfrac{\mathrm{\pi }}{6},\dfrac{\mathrm{\pi }}{3}] $ 上单调递增,
则 $ \begin{cases}-\dfrac{\mathrm{\pi }\omega }{3}+\dfrac{2\mathrm{\pi }}{3}\geqslant 2k\mathrm{\pi },\\ \dfrac{2\mathrm{\pi }\omega }{3}+\dfrac{2\mathrm{\pi }}{3}\leqslant 2k\mathrm{\pi }+\mathrm{\pi },\end{cases}k\in \boldsymbol{Z} $ ,
得 $ \begin{cases}\omega \leqslant -6k+2,\\ \omega \leqslant 3k+\dfrac{1}{2},\end{cases}k\in \boldsymbol{Z} $ ,
由于 $ k\in \boldsymbol{Z} $ ,且 $ \omega > 0 $ ,故 $ k=0 $ , $ 0 < \omega \leqslant \dfrac{1}{2} $ ,故④错误.故选 $ \mathrm{A} $ .
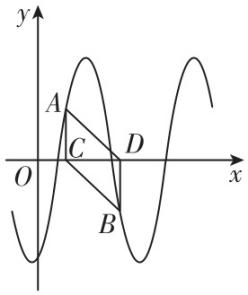
7.(多选)已知函数 $ f(x)=4 \sin (\omega x+\varphi )(\omega > 0,|\varphi | < \dfrac{\mathrm{\pi }}{2}) $ 的图象如图所示,点 $ A(\dfrac{\mathrm{\pi }}{6},2) $ , $ B $ 在 $ f(x) $ 的图象上 $ (A $ , $ B $ 位置如图所示 $ ) $ ,过 $ A $ , $ B $ 分别作 $ x $ 轴的垂线,垂足分别为 $ C $ , $ D $ ,若四边形 $ ACBD $ 为平行四边形,且面积为 $ \dfrac{2\mathrm{\pi }}{3} $ ,则下列结论正确的有( )
 (多选)
(多选)
A. $ T=\mathrm{\pi } $
B. $ f(x)=4 \sin (3x-\dfrac{\mathrm{\pi }}{3}) $
C. $ f(x) $ 在区间 $ [-\dfrac{\mathrm{\pi }}{18},\dfrac{5\mathrm{\pi }}{18}] $ 上单调递增
D. $ f(x) $ 的图象关于直线 $ x=\dfrac{4\mathrm{\pi }}{9} $ 对称
答案:BC
解析:四边形 $ ACBD $ 为平行四边形, $ AC=2 $ ,设 $ B({x}_{0},-2) $ ,
则 $ 2({x}_{0}-\dfrac{\mathrm{\pi }}{6})=\dfrac{2\mathrm{\pi }}{3} $ ,
所以 $ {x}_{0}-\dfrac{\mathrm{\pi }}{6}=\dfrac{\mathrm{\pi }}{3} $ ,则 $ \dfrac{T}{2}=\dfrac{1}{2}\cdot \dfrac{2\mathrm{\pi }}{\omega }=\dfrac{\mathrm{\pi }}{3} $ ,解得 $ \omega =3 $ ,故 $ f(x) $ 的周期为 $ \dfrac{2\mathrm{\pi }}{3} $ , $ \mathrm{A} $ 错误;
$ f(x)=4 \sin (3x+\varphi ) $ ,将点 $ A(\dfrac{\mathrm{\pi }}{6},2) $ 的坐标代入得, $ 4 \sin (3×\dfrac{\mathrm{\pi }}{6}+\varphi )=2 $ ,
即 $ \sin (\dfrac{\mathrm{\pi }}{2}+\varphi )=\dfrac{1}{2} $ ,由于点 $ A $ 在 $ f(x) $ 的单调递增区间上,
所以 $ \dfrac{\mathrm{\pi }}{2}+\varphi =2k\mathrm{\pi }+\dfrac{\mathrm{\pi }}{6} $ , $ k\in \boldsymbol{Z} $ ,
解得 $ \varphi =2k\mathrm{\pi }-\dfrac{\mathrm{\pi }}{3} $ , $ k\in \boldsymbol{Z} $ ,
所以 $ f(x)=4 \sin (3x+2k\mathrm{\pi }-\dfrac{\mathrm{\pi }}{3})=4 \sin (3x-\dfrac{\mathrm{\pi }}{3}) $ ,故 $ \mathrm{B} $ 正确;
当 $ x\in [-\dfrac{\mathrm{\pi }}{18},\dfrac{5\mathrm{\pi }}{18}] $ 时, $ 3x-\dfrac{\mathrm{\pi }}{3}\in [-\dfrac{\mathrm{\pi }}{2},\dfrac{\mathrm{\pi }}{2}] $ ,则由正弦函数的性质可知, $ f(x) $ 在区间 $ [-\dfrac{\mathrm{\pi }}{18},\dfrac{5\mathrm{\pi }}{18}] $ 上单调递增, $ \mathrm{C} $ 正确;
由于 $ f(\dfrac{4\mathrm{\pi }}{9})=4 \sin (3×\dfrac{4\mathrm{\pi }}{9}-\dfrac{\mathrm{\pi }}{3})=0 $ ,
所以直线 $ x=\dfrac{4\mathrm{\pi }}{9} $ 不是函数 $ f(x) $ 图象的对称轴, $ \mathrm{D} $ 错误.故选 $ \mathrm{B}\mathrm{C} $ .
8.已知函数 $ f(x)= \sin (\omega x+\varphi )(\omega > 0) $ ,且 $ f(x) $ 在区间 $ (\dfrac{2\mathrm{\pi }}{3},\dfrac{5\mathrm{\pi }}{6}) $ 上单调递减,则下列结论正确的有( )(多选)
A. $ f(x) $ 的最小正周期是 $ \dfrac{\mathrm{\pi }}{3} $
B.若 $ f(\dfrac{2\mathrm{\pi }}{3})+f(\dfrac{5\mathrm{\pi }}{6})=0 $ ,则 $ f(\dfrac{3\mathrm{\pi }}{4})=0 $
C.若 $ f(x+\dfrac{\mathrm{\pi }}{3})\geqslant f(x) $ 恒成立,则满足条件的 $ \omega $ 有且仅有1个
D.若 $ \varphi =-\dfrac{\mathrm{\pi }}{6} $ ,则 $ \omega $ 的取值范围是 $ [1,2]\cup [4,\dfrac{22}{5}] $
答案:BCD
解析:对于 $ \mathrm{A} $ ,因为函数 $ f(x) $ 在区间 $ (\dfrac{2\mathrm{\pi }}{3},\dfrac{5\mathrm{\pi }}{6}) $ 上单调递减,所以 $ \dfrac{T}{2}\geqslant \dfrac{5\mathrm{\pi }}{6}-\dfrac{2\mathrm{\pi }}{3}=\dfrac{\mathrm{\pi }}{6} $ ,所以 $ f(x) $ 的最小正周期 $ T\geqslant \dfrac{\mathrm{\pi }}{3} $ ,即 $ f(x) $ 的最小正周期的最小值为 $ \dfrac{\mathrm{\pi }}{3} $ ,故 $ \mathrm{A} $ 错误;
对于 $ \mathrm{B} $ ,因为 $ f(\dfrac{2\mathrm{\pi }}{3})+f(\dfrac{5\mathrm{\pi }}{6})=0 $ ,所以 $ f(x) $ 的图象关于点 $ (\dfrac{3\mathrm{\pi }}{4},0) $ 对称,所以 $ f(\dfrac{3\mathrm{\pi }}{4})=0 $ ,故 $ \mathrm{B} $ 正确;
对于 $ \mathrm{C} $ ,若 $ f(x+\dfrac{\mathrm{\pi }}{3})\geqslant f(x) $ 恒成立,则 $ \dfrac{\mathrm{\pi }}{3} $ 为函数 $ f(x) $ 的周期或周期的倍数,所以 $ k\cdot \dfrac{2\mathrm{\pi }}{\omega }=\dfrac{\mathrm{\pi }}{3} $ , $ k\in \boldsymbol{Z}(k\ne 0) $ ,所以 $ \omega =6k $ , $ k\in \boldsymbol{Z}(k\ne 0) $ ,因为 $ T\geqslant \dfrac{\mathrm{\pi }}{3} $ ,所以 $ \omega =\dfrac{2\mathrm{\pi }}{T}\leqslant 6 $ ,又 $ \omega > 0 $ ,所以 $ 0 < \omega \leqslant 6 $ ,所以 $ \omega =6 $ ,即满足条件的 $ \omega $ 有且仅有1个,故 $ \mathrm{C} $ 正确;
对于 $ \mathrm{D} $ ,由题意可知 $ (\dfrac{2\mathrm{\pi }}{3},\dfrac{5\mathrm{\pi }}{6}) $ 为 $ f(x)= \sin (\omega x-\dfrac{\mathrm{\pi }}{6}) $ 单调递减区间的子集,
所以 $ \begin{cases}\dfrac{2\mathrm{\pi }}{3}\omega -\dfrac{\mathrm{\pi }}{6}\geqslant \dfrac{\mathrm{\pi }}{2}+2k\mathrm{\pi },\\ \dfrac{5\mathrm{\pi }}{6}\omega -\dfrac{\mathrm{\pi }}{6}\leqslant \dfrac{3\mathrm{\pi }}{2}+2k\mathrm{\pi },\end{cases} $ 其中 $ k\in \boldsymbol{Z} $ ,解得 $ 3k+1\leqslant \omega \leqslant \dfrac{12k}{5}+2 $ , $ k\in \boldsymbol{Z} $ ,
当 $ k=0 $ 时, $ 1\leqslant \omega \leqslant 2 $ ,当 $ k=1 $ 时, $ 4\leqslant \omega \leqslant \dfrac{22}{5} $ ,故 $ \omega $ 的取值范围是 $ [1,2]\cup [4,\dfrac{22}{5}] $ ,故 $ \mathrm{D} $ 正确.故选 $ \mathrm{B}\mathrm{C}\mathrm{D} $ .
9.已知函数 $ f(x)= \tan (\omega x-\varphi )(\omega > 0) $ 的最小正周期为 $ \dfrac{\mathrm{\pi }}{3} $ ,写出满足“将函数 $ f(x) $ 的图象向左平移 $ \dfrac{\mathrm{\pi }}{12} $ 个单位长度后,得到的图象对应的函数为奇函数”的 $ \varphi $ 的一个值为 .
答案: $ \dfrac{\mathrm{\pi }}{4} $ (答案不唯一)
解析:函数 $ f(x)= \tan (\omega x-\varphi )(\omega > 0) $ 的最小正周期为 $ T=\dfrac{\mathrm{\pi }}{\omega }=\dfrac{\mathrm{\pi }}{3} $ ,可得 $ \omega =3 $ ,所以 $ f(x)= \tan (3x-\varphi ) $ .将其图象向左平移 $ \dfrac{\mathrm{\pi }}{12} $ 个单位长度后,得到 $ y= \tan [3(x+\dfrac{\mathrm{\pi }}{12})-\varphi ]= \tan (3x+\dfrac{\mathrm{\pi }}{4}-\varphi ) $ 的图象,
因为所得函数为奇函数,所以 $ \dfrac{\mathrm{\pi }}{4}-\varphi =\dfrac{k\mathrm{\pi }}{2} $ , $ k\in \boldsymbol{Z} $ ,解得 $ \varphi =\dfrac{\mathrm{\pi }}{4}-\dfrac{k\mathrm{\pi }}{2} $ , $ k\in \boldsymbol{Z} $ ,
故可取 $ \varphi $ 的一个值为 $ \dfrac{\mathrm{\pi }}{4} $ .
10.将函数 $ f(x)= \sin x \cos x $ 的图象向左平移 $ \dfrac{\mathrm{\pi }}{6} $ 个单位长度,再将横坐标变为原来的4倍,纵坐标变为原来的 $ 2\sqrt{2} $ 倍,得到函数 $ g(x) $ 的图象,则函数 $ g(x) $ 的最小正周期为 .
解析: $ f(x)= \sin x \cos x=\dfrac{1}{2} \sin 2x $ ,
将 $ f(x) $ 的图象向左平移 $ \dfrac{\mathrm{\pi }}{6} $ 个单位长度可得 $ y=\dfrac{1}{2} \sin [2(x+\dfrac{\mathrm{\pi }}{6})]=\dfrac{1}{2} \sin (2x+\dfrac{\mathrm{\pi }}{3}) $ 的图象,
将 $ y=\dfrac{1}{2} \sin (2x+\dfrac{\mathrm{\pi }}{3}) $ 的图象上点的横坐标变为原来的4倍可得 $ y=\dfrac{1}{2} \sin (\dfrac{1}{2}x+\dfrac{\mathrm{\pi }}{3}) $ 的图象,
将 $ y=\dfrac{1}{2} \sin (\dfrac{1}{2}x+\dfrac{\mathrm{\pi }}{3}) $ 的图象上点的纵坐标变为原来的 $ 2\sqrt{2} $ 倍可得 $ g(x)=\sqrt{2} \sin (\dfrac{1}{2}x+\dfrac{\mathrm{\pi }}{3}) $ 的图象,
所以 $ g(x) $ 的最小正周期 $ T=\dfrac{2\mathrm{\pi }}{\dfrac{1}{2}}=4\mathrm{\pi } $ .
11.已知函数 $ f(x)=2 \sin \text{ }\omega x \cos (\omega x+\varphi )(\omega > 0,\left|\varphi \right|\leqslant \dfrac{\mathrm{\pi }}{2}) $ .当 $ \omega =1 $ , $ \varphi =\dfrac{\mathrm{\pi }}{6} $ 时, $ f(x) $ 的单调递增区间为 .设函数 $ g(x)=f(x)+ \sin \text{ }\varphi $ ,若 $ x=-\dfrac{\mathrm{\pi }}{8} $ 是 $ g(x) $ 的零点,直线 $ x=\dfrac{\mathrm{\pi }}{8} $ 是 $ g(x) $ 图象的对称轴,且 $ g(x) $ 在区间 $ (\dfrac{\mathrm{\pi }}{18},\dfrac{\mathrm{\pi }}{9}) $ 上无最值,则 $ \omega $ 的最大值为 .
答案: $ [k\mathrm{\pi }-\dfrac{\mathrm{\pi }}{3},k\mathrm{\pi }+\dfrac{\mathrm{\pi }}{6}](k\in \mathbf{Z}) $ ;7
解析:依题意, $ f(x)=2 \sin \text{ }\omega x( \cos \text{ }\omega x\cdot \cos \text{ }\varphi - \sin \text{ }\omega x \sin \text{ }\varphi )= \sin \text{ }2\omega x \cos \text{ }\varphi -(1- \cos \text{ }2\omega x)\cdot \sin \text{ }\varphi = \sin (2\omega x+\varphi )- \sin \text{ }\varphi $ ,
当 $ \omega =1 $ , $ \varphi =\dfrac{\mathrm{\pi }}{6} $ 时, $ f(x)= \sin (2x+\dfrac{\mathrm{\pi }}{6})-\dfrac{1}{2} $ ,由 $ 2k\mathrm{\pi }-\dfrac{\mathrm{\pi }}{2}\leqslant 2x+\dfrac{\mathrm{\pi }}{6}\leqslant 2k\mathrm{\pi }+\dfrac{\mathrm{\pi }}{2} $ , $ k\in \mathbf{Z} $ ,得 $ k\mathrm{\pi }-\dfrac{\mathrm{\pi }}{3}\leqslant x\leqslant k\mathrm{\pi }+\dfrac{\mathrm{\pi }}{6} $ , $ k\in \mathbf{Z} $ ,所以 $ f(x) $ 的单调递增区间为 $ [k\mathrm{\pi }-\dfrac{\mathrm{\pi }}{3},k\mathrm{\pi }+\dfrac{\mathrm{\pi }}{6}](k\in \mathbf{Z}) $ .
$ g(x)=f(x)+ \sin \text{ }\varphi = \sin (2\omega x+\varphi ) $ ,依题意 $ -\dfrac{\mathrm{\pi }}{4}\omega +\varphi ={k}_{1}\mathrm{\pi } $ , $ {k}_{1}\in \mathbf{Z} $ , $ \dfrac{\mathrm{\pi }}{4}\omega +\varphi ={k}_{2}\mathrm{\pi }+\dfrac{\mathrm{\pi }}{2} $ , $ {k}_{2}\in \mathbf{Z} $ ,则有 $ \omega =2({k}_{2}-{k}_{1})+1 $ , $ {k}_{1} $ , $ {k}_{2}\in \mathbf{Z} $ ,而 $ \omega > 0 $ ,即有 $ \omega =2n+1 $ , $ n\in \mathrm{N} $ .
因为 $ g(x) $ 在区间 $ (\dfrac{\mathrm{\pi }}{18},\dfrac{\mathrm{\pi }}{9}) $ 上无最值,
则 $ g(x) $ 的周期 $ \dfrac{2\mathrm{\pi }}{2\omega }=T\geqslant 2×(\dfrac{\mathrm{\pi }}{9}-\dfrac{\mathrm{\pi }}{18})=\dfrac{\mathrm{\pi }}{9} $ ,即 $ 0 < \omega \leqslant 9 $ .
当 $ \omega =9 $ 时, $ \dfrac{9\mathrm{\pi }}{4}+\varphi ={k}_{2}\mathrm{\pi }+\dfrac{\mathrm{\pi }}{2} $ , $ {k}_{2}\in \mathbf{Z} $ ,而 $ \left|\varphi \right|\leqslant \dfrac{\mathrm{\pi }}{2} $ ,则 $ {k}_{2}=2 $ , $ \varphi =\dfrac{\mathrm{\pi }}{4} $ , $ g(x)= \sin (18x+\dfrac{\mathrm{\pi }}{4}) $ ,当 $ \dfrac{\mathrm{\pi }}{18} < x < \dfrac{\mathrm{\pi }}{9} $ 时, $ \dfrac{5\mathrm{\pi }}{4} < 18x+\dfrac{\mathrm{\pi }}{4} < \dfrac{9\mathrm{\pi }}{4} $ ,因此当 $ 18x+\dfrac{\mathrm{\pi }}{4}=\dfrac{3\mathrm{\pi }}{2} $ ,即 $ x=\dfrac{5\mathrm{\pi }}{72} $ 时, $ g(x) $ 取得最小值,不符合题意,
当 $ \omega =7 $ 时, $ \dfrac{7\mathrm{\pi }}{4}+\varphi ={k}_{2}\mathrm{\pi }+\dfrac{\mathrm{\pi }}{2} $ , $ {k}_{2}\in \mathbf{Z} $ ,而 $ \left|\varphi \right|\leqslant \dfrac{\mathrm{\pi }}{2} $ ,则 $ {k}_{2}=1 $ , $ \varphi =-\dfrac{\mathrm{\pi }}{4} $ , $ g(x)= \sin (14x-\dfrac{\mathrm{\pi }}{4}) $ ,
当 $ \dfrac{\mathrm{\pi }}{18} < x < \dfrac{\mathrm{\pi }}{9} $ 时, $ \dfrac{19\mathrm{\pi }}{36} < 14x-\dfrac{\mathrm{\pi }}{4} < \dfrac{47\mathrm{\pi }}{36} $ ,而 $ (\dfrac{19\mathrm{\pi }}{36},\dfrac{47\mathrm{\pi }}{36})\subseteq (\dfrac{\mathrm{\pi }}{2},\dfrac{3\mathrm{\pi }}{2}) $ ,因此 $ g(x) $ 在 $ (\dfrac{\mathrm{\pi }}{18},\dfrac{\mathrm{\pi }}{9}) $ 上单调,无最值,所以 $ \omega $ 的最大值为7.
12.已知函数 $ f (x )=A \sin (\omega x+\varphi ) (A > 0 $ , $ \omega > 0 $ , $ -\dfrac{\mathrm{\pi }}{2} < \varphi < \dfrac{\mathrm{\pi }}{2}) $ 在一个周期内的图象如图所示.
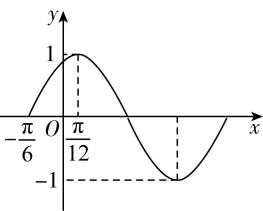
(1) 求函数 $ f(x) $ 的最小正周期 $ T $ 及 $ f(x) $ 的解析式;
(2) 求函数 $ f(x) $ 的图象的对称轴方程及单调递增区间;
(3) 将 $ f(x) $ 的图象向右平移 $ \dfrac{\mathrm{\pi }}{3} $ 个单位长度,再将所得图象上所有点的横坐标伸长为原来的2倍(纵坐标不变),得到函数 $ g(x) $ 的图象,若 $ g(x)=a-1 $ 在 $ [\dfrac{\mathrm{\pi }}{2},\dfrac{3\mathrm{\pi }}{2}] $ 上有两个解,求实数 $ a $ 的取值范围.
答案:(1) 【解】由题图可知, $ A=1 $ , $ \dfrac{T}{4}=\dfrac{\mathrm{\pi }}{12}+\dfrac{\mathrm{\pi }}{6}=\dfrac{\mathrm{\pi }}{4}⇒T=\mathrm{\pi } $ ,则 $ \dfrac{2\mathrm{\pi }}{\omega }=\mathrm{\pi }⇒\omega =2 $ ,
所以 $ f(x)= \sin (2x+\varphi ) $ .
又因为 $ f(x) $ 的图象过点 $ (\dfrac{\mathrm{\pi }}{12},1) $ ,所以 $ 2×\dfrac{\mathrm{\pi }}{12}+\varphi =\dfrac{\mathrm{\pi }}{2}+2k\mathrm{\pi }(k\in \boldsymbol{Z}) $ ,可得 $ \varphi =\dfrac{\mathrm{\pi }}{3}+2k\mathrm{\pi }(k\in \boldsymbol{Z}) $ ,
而 $ -\dfrac{\mathrm{\pi }}{2} < \varphi < \dfrac{\mathrm{\pi }}{2} $ ,则 $ \varphi =\dfrac{\mathrm{\pi }}{3} $ ,
于是 $ f(x)= \sin (2x+\dfrac{\mathrm{\pi }}{3}) $ .
(2) 【解】结合题图可知,函数 $ f(x) $ 图象的对称轴方程为 $ x=\dfrac{\mathrm{\pi }}{12}+\dfrac{k\mathrm{\pi }}{2}(k\in \boldsymbol{Z}) $ .
令 $ -\dfrac{\mathrm{\pi }}{2}+2k\mathrm{\pi }\leqslant 2x+\dfrac{\mathrm{\pi }}{3}\leqslant \dfrac{\mathrm{\pi }}{2}+2k\mathrm{\pi }(k\in \boldsymbol{Z}) $ ,解得 $ -\dfrac{5}{12}\mathrm{\pi }+k\mathrm{\pi }\leqslant x\leqslant \dfrac{\mathrm{\pi }}{12}+k\mathrm{\pi }(k\in \boldsymbol{Z}) $ ,
所以函数 $ f(x) $ 的单调递增区间为 $ [-\dfrac{5}{12}\mathrm{\pi }+k\mathrm{\pi } $ , $ \dfrac{\mathrm{\pi }}{12}+k\mathrm{\pi } ] (k\in \boldsymbol{Z} ) $ .
(3) 【解】 $ f(x) $ 的图象向右平移 $ \dfrac{\mathrm{\pi }}{3} $ 个单位长度得到 $ y= \sin [2(x-\dfrac{\mathrm{\pi }}{3})+\dfrac{\mathrm{\pi }}{3}]= \sin (2x-\dfrac{\mathrm{\pi }}{3}) $ 的图象,再将所得图象上所有点的横坐标伸长为原来的2倍(纵坐标不变),得到 $ g(x)= \sin (x-\dfrac{\mathrm{\pi }}{3}) $ 的图象,则 $ g(x) $ 在 $ [\dfrac{\mathrm{\pi }}{2},\dfrac{3\mathrm{\pi }}{2}] $ 上的图象如图所示.

因为 $ g(x)=a-1 $ 在 $ [\dfrac{\mathrm{\pi }}{2},\dfrac{3\mathrm{\pi }}{2}] $ 上有两个解,所以 $ \dfrac{1}{2}\leqslant a-1 < 1 $ ,解得 $ \dfrac{3}{2}\leqslant a < 2 $ ,
即实数 $ a $ 的取值范围为 $ [\dfrac{3}{2},2) $ .
解析:

 (多选)
(多选)
