5.7 三角函数的应用
一、刷基础
1.已知简谐运动 $ f(x)=2 \sin (\dfrac{\mathrm{\pi }}{3}x+\varphi )(\left|\varphi \right| < \dfrac{\mathrm{\pi }}{2}) $ 的图象经过点 $ (0,1) $ ,则该简谐运动的最小正周期 $ T $ 和初相 $ \varphi $ 分别为( )
A. $ T=6 $ , $ \varphi =\dfrac{\mathrm{\pi }}{6} $
B. $ T=6 $ , $ \varphi =\dfrac{\mathrm{\pi }}{3} $
C. $ T=6\mathrm{\pi } $ , $ \varphi =\dfrac{\mathrm{\pi }}{6} $
D. $ T=6\mathrm{\pi } $ , $ \varphi =\dfrac{\mathrm{\pi }}{3} $
答案:A
解析: $ T=\dfrac{2\mathrm{\pi }}{\omega }=\dfrac{2\mathrm{\pi }}{\dfrac{\mathrm{\pi }}{3}}=6 $ .
$ \because f(x) $ 的图象经过点 $ (0,1) $ , $ \therefore \sin \text{ }\varphi =\dfrac{1}{2} $ .
又 $ \because -\dfrac{\mathrm{\pi }}{2} < \varphi < \dfrac{\mathrm{\pi }}{2} $ , $ \therefore \varphi =\dfrac{\mathrm{\pi }}{6} $ .
2.将塑料瓶底部扎一个小孔做成漏斗,再挂在架子上,就做成了一个简易单摆.在漏斗下放纸板,板的中间画一条直线作为坐标系的横轴,把漏斗灌上细沙并拉离平衡位置,放手使它摆动,同时匀速拉动纸板,这样就可在纸板上得到一条曲线,它就是简谐运动的图象.它表示了漏斗对平衡位置的位移 $ s $ (纵坐标)随时间 $ t $ (横坐标)变化的情况.如图所示,已知一根长为 $ l\mathrm{c}\mathrm{m} $ 的线一端固定,另一端悬一个漏斗,漏斗摆动时离开平衡位置的位移 $ s $ (单位: $ \mathrm{c}\mathrm{m} $ )与时间 $ t $ (单位: $ \mathrm{s} $ )的函数关系是 $ s=2 \cos 2\sqrt{\dfrac{g}{l}}t $ ,其中 $ g\approx 980\mathrm{c}\mathrm{m}/{\mathrm{s}}^{2} $ , $ \mathrm{\pi }\approx 3 $ ,则估计线的长度应当是(精确到 $ 0.1\mathrm{c}\mathrm{m} $ )( )
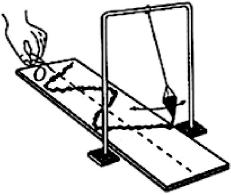
A. $ 15.4\mathrm{c}\mathrm{m} $
B. $ 16.4\mathrm{c}\mathrm{m} $
C. $ 17.4\mathrm{c}\mathrm{m} $
D. $ 18.4\mathrm{c}\mathrm{m} $
答案:C
解析:由 $ s=2 \cos 2\sqrt{\dfrac{g}{l}}t $ ,得 $ T=\dfrac{2\mathrm{\pi }}{2\sqrt{\dfrac{g}{l}}}=\dfrac{\mathrm{\pi }}{\sqrt{\dfrac{g}{l}}} $ .
由函数的图象可知函数的周期为 $ 0.4 $ ,所以 $ \dfrac{\mathrm{\pi }}{\sqrt{\dfrac{g}{l}}}=0.4 $ ,即 $ l=\dfrac{0.16g}{{\mathrm{\pi }}^{2}}\approx \dfrac{0.16×980}{{3}^{2}}\approx 17.4\mathrm{c}\mathrm{m} $ .故选 $ \mathrm{C} $ .
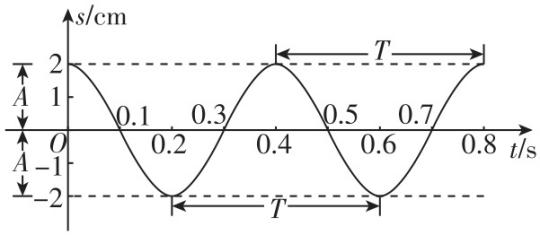
3.阻尼器是一种以提供阻力达到减震效果的专业工程装置.我国第一高楼上海中心大厦的阻尼器减震装置,被称为“上海慧眼”,如图①.由物理学知识可知,某阻尼器的运动过程可近似为单摆运动,其离开平衡位置的位移 $ y $ (单位: $ \mathrm{m} $ )和时间 $ t $ (单位: $ \mathrm{s} $ )的函数关系为 $ y= \sin (\omega t+\varphi )(\omega > 0,|\varphi | < \mathrm{\pi }) $ ,如图②,若该阻尼器在摆动过程中连续三次位移为 $ {s}_{0}(-1 < {s}_{0} < 1) $ 的时间分别为 $ {t}_{1} $ , $ {t}_{2} $ , $ {t}_{3}(0 < {t}_{1} < {t}_{2} < {t}_{3}) $ ,且 $ {t}_{1}+{t}_{2}=2 $ , $ {t}_{2}+{t}_{3}=5 $ ,则在一个周期内阻尼器离开平衡位置的正向位移大于 $ 0.5\mathrm{m} $ 的总时间为( )
A. $ \dfrac{1}{3}\mathrm{s} $
B. $ \dfrac{2}{3}\mathrm{s} $
C. $ 1\mathrm{s} $
D. $ \dfrac{4}{3}\mathrm{s} $
答案:C
解析:因为 $ {t}_{1}+{t}_{2}=2 $ , $ {t}_{2}+{t}_{3}=5 $ ,所以 $ {t}_{3}-{t}_{1}=3 $ ,所以最小正周期 $ T=3 $ .
又 $ T=\dfrac{2\mathrm{\pi }}{\omega } $ ,所以 $ \omega =\dfrac{2\mathrm{\pi }}{3} $ ,则 $ y= \sin (\dfrac{2\mathrm{\pi }}{3}t+\varphi ) $ .
由 $ y > 0.5 $ 可得 $ \sin (\dfrac{2\mathrm{\pi }}{3}t+\varphi ) > 0.5 $ ,
所以 $ 2k\mathrm{\pi }+\dfrac{\mathrm{\pi }}{6} < \dfrac{2\mathrm{\pi }}{3}t+\varphi < \dfrac{5\mathrm{\pi }}{6}+2k\mathrm{\pi } $ , $ k\in \boldsymbol{Z} $ ,可得 $ 3k+\dfrac{1}{4}-\dfrac{3}{2\mathrm{\pi }}\varphi < t < \dfrac{5}{4}-\dfrac{3}{2\mathrm{\pi }}\varphi +3k $ , $ k\in \boldsymbol{Z} $ .
因为 $ (3k+\dfrac{5}{4}-\dfrac{3}{2\mathrm{\pi }}\varphi )-(3k+\dfrac{1}{4}-\dfrac{3}{2\mathrm{\pi }}\varphi )=1 $ ,
所以在一个周期内阻尼器离开平衡位置的正向位移大于 $ 0.5\mathrm{m} $ 的总时间为 $ 1\mathrm{s} $ .故选 $ \mathrm{C} $ .
4.(多选)已知一正弦电流 $ I $ (单位:A)随时间 $ t $ (单位: $ \mathrm{s} $ )变化的函数 $ I=A \sin (\omega t+\varphi ) (A > 0 $ , $ \omega > 0 $ , $ |\varphi | < \dfrac{\mathrm{\pi }}{2}) $ 的部分图象如图所示,则( )
 (多选)
(多选)
A. $ A=60 $
B. $ \omega =\dfrac{50\mathrm{\pi }}{3} $
C. $ \varphi =\dfrac{\mathrm{\pi }}{6} $
D.在一个周期内,电流不超过 $ 30\mathrm{A} $ 的时长为 $ \dfrac{2}{25}\mathrm{s} $
答案:AB
解析:对于 $ \mathrm{A} $ ,由题图可知 $ A=60 $ ,故 $ \mathrm{A} $ 正确.
对于 $ \mathrm{B} $ ,由 $ \dfrac{T}{4}=\dfrac{1}{10}-\dfrac{7}{100}=\dfrac{3}{100} $ ,得 $ T=\dfrac{3}{25} $ ,则 $ \omega =\dfrac{2\mathrm{\pi }}{T}=\dfrac{50\mathrm{\pi }}{3} $ ,故 $ \mathrm{B} $ 正确.
对于 $ \mathrm{C} $ ,由题图可知函数 $ I=A \sin (\omega t+\varphi ) $ 的图象过点 $ (\dfrac{1}{10},-60) $ ,故 $ 60 \sin (\dfrac{50\mathrm{\pi }}{3}×\dfrac{1}{10}+\varphi )=-60 $ ,则 $ \dfrac{5\mathrm{\pi }}{3}+\varphi =\dfrac{3\mathrm{\pi }}{2}+2k\mathrm{\pi }(k\in \boldsymbol{Z}) $ ,得 $ \varphi =-\dfrac{\mathrm{\pi }}{6}+2k\mathrm{\pi }(k\in \boldsymbol{Z}) $ .
因为 $ |\varphi | < \dfrac{\mathrm{\pi }}{2} $ ,所以 $ \varphi =-\dfrac{\mathrm{\pi }}{6} $ ,故 $ \mathrm{C} $ 错误.
对于 $ \mathrm{D} $ ,由 $ -30\leqslant 60 \sin (\dfrac{50\mathrm{\pi }}{3}t-\dfrac{\mathrm{\pi }}{6})\leqslant 30 $ ,得 $ -\dfrac{1}{2}\leqslant \sin (\dfrac{50\mathrm{\pi }}{3}t-\dfrac{\mathrm{\pi }}{6})\leqslant \dfrac{1}{2} $ ,
则 $ -\dfrac{\mathrm{\pi }}{6}+2k\mathrm{\pi }\leqslant \dfrac{50\mathrm{\pi }}{3}t-\dfrac{\mathrm{\pi }}{6}\leqslant \dfrac{\mathrm{\pi }}{6}+2k\mathrm{\pi }(k\in \boldsymbol{Z}) $ 或 $ \dfrac{5\mathrm{\pi }}{6}+2k\mathrm{\pi }\leqslant \dfrac{50\mathrm{\pi }}{3}t-\dfrac{\mathrm{\pi }}{6}\leqslant \dfrac{7\mathrm{\pi }}{6}+2k\mathrm{\pi }(k\in \boldsymbol{Z}) $ , $ \dfrac{3}{25}k\leqslant t\leqslant \dfrac{1}{50}+\dfrac{3}{25}k(k\in \boldsymbol{Z}) $ 或 $ \dfrac{3}{50}+\dfrac{3}{25}k\leqslant t\leqslant \dfrac{2}{25}+\dfrac{3}{25}k(k\in \boldsymbol{Z}) $ ,
所以在一个周期内,电流不超过 $ 30\mathrm{A} $ 的时长为 $ \dfrac{1}{50}×2=\dfrac{1}{25}(\mathrm{s}) $ ,故 $ \mathrm{D} $ 错误.故选 $ \mathrm{A}\mathrm{B} $ .
5.已知某地区某天的温度(单位: $ \mathrm{℃} $ )随时间 $ t $ (单位: $ \mathrm{h} $ )的变化近似满足函数关系 $ f(t)=28+A \sin (\dfrac{\mathrm{\pi }}{8}t+\dfrac{3\mathrm{\pi }}{4})(A > 0) $ , $ t\in [0,24) $ ,且这天的最大温差为 $ 8\mathrm{℃} $ ,则 $ A= $ ;若温度不低于 $ 30\mathrm{℃} $ 需要开空调降温,则这天需要降温的时长为 $ \mathrm{h} $ .
解析: $ f(t)=28+A \sin (\dfrac{\mathrm{\pi }}{8}t+\dfrac{3\mathrm{\pi }}{4})(A > 0) $ ,其最小正周期 $ T=\dfrac{2\mathrm{\pi }}{\dfrac{\mathrm{\pi }}{8}}=16 < 24 $ ,
故这天的最大温差即为 $ f(t) $ 的最大值与最小值的差,又 $ A > 0 $ ,故 $ (A+28)-(-A+28)=2A=8 $ ,解得 $ A=4 $ .
令 $ f(t)\geqslant 30 $ ,即 $ 4 \sin (\dfrac{\mathrm{\pi }}{8}t+\dfrac{3}{4}\mathrm{\pi })+28\geqslant 30 $ , $ \sin (\dfrac{\mathrm{\pi }}{8}t+\dfrac{3}{4}\mathrm{\pi })\geqslant \dfrac{1}{2} $ ,又 $ t\in [0,24) $ ,则 $ \dfrac{\mathrm{\pi }}{8}t+\dfrac{3}{4}\mathrm{\pi }\in [\dfrac{3}{4}\mathrm{\pi },\dfrac{15\mathrm{\pi }}{4}) $ ,
则 $ \dfrac{3}{4}\mathrm{\pi }\leqslant \dfrac{\mathrm{\pi }}{8}t+\dfrac{3}{4}\mathrm{\pi }\leqslant \dfrac{5\mathrm{\pi }}{6} $ 或 $ \dfrac{13\mathrm{\pi }}{6}\leqslant \dfrac{\mathrm{\pi }}{8}t+\dfrac{3}{4}\mathrm{\pi }\leqslant \dfrac{17}{6}\mathrm{\pi } $ ,解得 $ t\in [0,\dfrac{2}{3}]\cup [\dfrac{34}{3},\dfrac{50}{3}] $ ,
则一天中需要降温的时长为 $ \dfrac{2}{3}+(\dfrac{50}{3}-\dfrac{34}{3})=6(\mathrm{h}) $ .
6.(多选)筒车是我国古代发明的一种水利灌溉工具,因其经济又环保,至今还在农业生产中使用(图①),明朝科学家徐光启在《农政全书》中用图画描绘了筒车的工作原理(图②).若一半径为2米的筒车水轮的圆心 $ O $ 距离水面1米(图③),已知水轮按逆时针转动,每分钟匀速转动4圈,当水轮上点 $ P $ 从水中浮现时(图③中点 $ {P}_{0} $ 的位置)开始计时,点 $ P $ 距水面的高度(在水面上时为正值,在水面下时为负值) $ d $ (单位:米)与时间 $ x $ (单位:秒)的关系可以用 $ d=A \sin (\omega x+\varphi )+B (A > 0 $ , $ \omega > 0 $ , $ |\varphi | < \dfrac{\mathrm{\pi }}{2} $ , $ B\in \boldsymbol{R}) $ 表示.下列结论正确的有( )
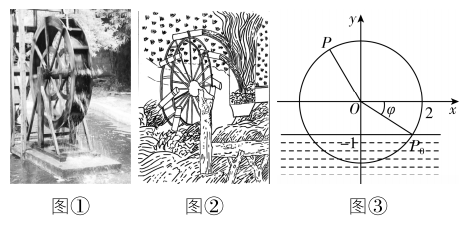 (多选)
(多选)
A. $ d=2 \sin (\dfrac{2\mathrm{\pi }}{15}x-\dfrac{\mathrm{\pi }}{3})+1 $
B.点 $ P $ 第一次到达最高点需用时5秒
C.点 $ P $ 再次接触水面需用时10秒
D.当点 $ P $ 运动2.5秒时,距水面的高度为1.5米
答案:BC
解析:由题意可得 $ \begin{cases}A+B=3,\\ -A+B=-1,\end{cases} $ 解得 $ \begin{cases}A=2,\\ B=1,\end{cases} $ 又 $ T=\dfrac{60}{4}=15 $ ,所以 $ \omega =\dfrac{2\mathrm{\pi }}{T}=\dfrac{2\mathrm{\pi }}{15} $ ,
当 $ x=0 $ 时, $ d=2 \sin \varphi +1=0 $ ,解得 $ \sin \varphi =-\dfrac{1}{2} $ ,因为 $ |\varphi | < \dfrac{\mathrm{\pi }}{2} $ ,所以 $ \varphi =-\dfrac{\mathrm{\pi }}{6} $ ,
所以 $ d=2 \sin (\dfrac{2\mathrm{\pi }}{15}x-\dfrac{\mathrm{\pi }}{6})+1 $ , $ \mathrm{A} $ 错误;
令 $ d=3 $ ,得 $ \sin (\dfrac{2\mathrm{\pi }}{15}x-\dfrac{\mathrm{\pi }}{6})=1 $ ,则 $ \dfrac{2\mathrm{\pi }}{15}x-\dfrac{\mathrm{\pi }}{6}=\dfrac{\mathrm{\pi }}{2}+2k\mathrm{\pi } $ , $ k\in \boldsymbol{Z} $ ,解得 $ x=5+15k $ , $ k\in \boldsymbol{Z} $ ,又 $ x > 0 $ ,所以 $ x $ 的最小值为5,即点 $ P $ 第一次到达最高点需用时5秒, $ \mathrm{B} $ 正确;
由题意知,点 $ P $ 再次接触水面需用时 $ \dfrac{2}{3}T=\dfrac{2}{3}×15=10 $ (秒), $ \mathrm{C} $ 正确;
当 $ x=2.5 $ 时, $ d=2 \sin (\dfrac{2\mathrm{\pi }}{15}×\dfrac{5}{2}-\dfrac{\mathrm{\pi }}{6})+1=2 $ ,故点 $ P $ 距水面的高度为2米, $ \mathrm{D} $ 错误.故选 $ \mathrm{B}\mathrm{C} $ .
7.一个大风车的半径为8米,风车按逆时针方向匀速旋转,并且每12分钟旋转一周,它的最低点离地面2米.设风车开始旋转时其翼片的一个端点 $ P $ 在风车的最低点,求:
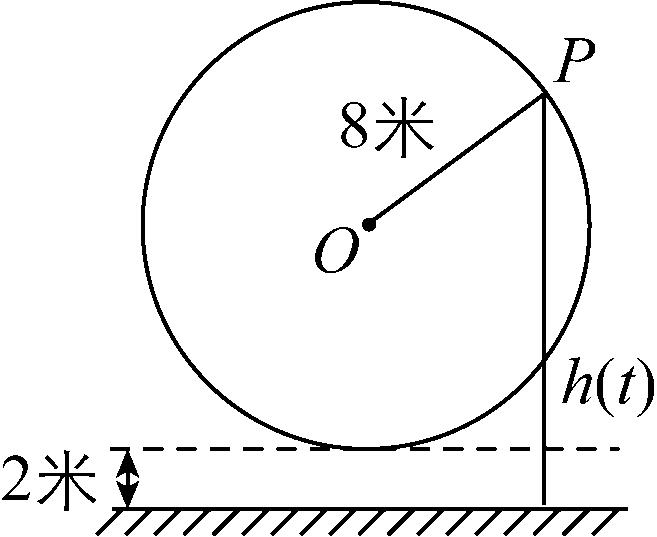
(1)点 $ P $ 离地面距离 $ h $ (米)与时间 $ t $ (分)之间的函数关系式.
(2)在第一圈的什么时间段,点 $ P $ 离地面的高度超过14米?
解析:(1)不妨设 $ h(t)=A \sin (\omega t+\varphi )+b $ , $ A > 0 $ , $ \omega > 0 $ ,由题意得 $ A=8 $ , $ T=12 $ , $ b=10 $ ,则 $ \omega =\dfrac{2\mathrm{\pi }}{T}=\dfrac{\mathrm{\pi }}{6} $ .
当 $ t=0 $ 时, $ h(0)=2 $ ,即 $ \sin \text{ }\varphi =-1 $ ,取 $ \varphi =-\dfrac{\mathrm{\pi }}{2} $ .
因此 $ h(t)=8 \sin (\dfrac{\mathrm{\pi }}{6}t-\dfrac{\mathrm{\pi }}{2})+10 $ , $ t\geqslant 0 $ .
(2)由题意令 $ h(t) > 14 $ ,即 $ 8 \sin (\dfrac{\mathrm{\pi }}{6}t-\dfrac{\mathrm{\pi }}{2})+10 > 14 $ ,则 $ \cos \dfrac{\mathrm{\pi }}{6}t < -\dfrac{1}{2} $ .
又因为 $ 0\leqslant t\leqslant 12 $ ,所以 $ 4 < t < 8 $ .
所以在第一圈的4分钟到8分钟内,点 $ P $ 离地面的高度超过14米.
8.近年来,西安市长安区认真践行“绿水青山就是金山银山”的生态文明理念,围绕良好的生态禀赋和市场需求,深挖冷水鱼产业发展优势潜力,摸索出以虹鳟、鲟鱼等养殖为主的方向.为扩大养殖规模,某鲟鱼养殖场计划在如图所示的扇形区域 $ OMN $ 内修建矩形水池 $ ABCD $ ,矩形一边 $ AB $ 在 $ OM $ 上,点 $ C $ 在圆弧 $ MN $ 上,点 $ D $ 在边 $ ON $ 上,且 $ \mathrm{\angle }MON=\dfrac{\mathrm{\pi }}{3} $ , $ OM=60 $ 米,设 $ \mathrm{\angle }COM=\alpha $ .
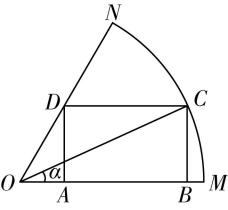
(1) 求扇形 $ OMN $ 的面积;
(2) 求矩形 $ ABCD $ 的面积 $ S(\alpha ) $ ,当 $ \alpha $ 为何值时, $ S(\alpha ) $ 取得最大值,并求出这个最大值.
答案:(1) 【解】依题意, $ \mathrm{\angle }MON=\dfrac{\mathrm{\pi }}{3} $ ,扇形半径 $ OM=60 $ 米,
则扇形 $ OMN $ 的面积为 $ \dfrac{1}{2}×\dfrac{\mathrm{\pi }}{3}×{60}^{2}=600\mathrm{\pi } $ 平方米.
(2) 【解】在 $ \mathrm{R}\mathrm{t}△OBC $ 中, $ BC=60 \sin \alpha $ , $ OB=60 \cos \alpha $ ,
在 $ \mathrm{R}\mathrm{t}△OAD $ 中, $ AD=BC=60 \sin \alpha $ ,则 $ OA=\dfrac{AD}{\sqrt{3}}=\dfrac{\sqrt{3}}{3}×60 \sin \alpha =20\sqrt{3} \sin \alpha $ ,
于是 $ AB=OB-OA=60 \cos \alpha -20\sqrt{3} \sin \alpha $ ,
则矩形 $ ABCD $ 的面积 $ S(\alpha )=AB\cdot BC $
$ =60 \sin \alpha (60 \cos \alpha -20\sqrt{3} \sin \alpha ) $
$ =1200\sqrt{3}(\sqrt{3} \sin \alpha \cos \alpha -{ \sin }^{2}\alpha ) $
$ =1200\sqrt{3}(\dfrac{\sqrt{3}}{2} \sin 2\alpha +\dfrac{1}{2} \cos 2\alpha -\dfrac{1}{2}) $
$ =1200\sqrt{3} \sin (2\alpha +\dfrac{\mathrm{\pi }}{6})-600\sqrt{3} $ ,
所以 $ S(\alpha )=1200\sqrt{3} \sin (2\alpha +\dfrac{\mathrm{\pi }}{6})-600\sqrt{3}(0 < \alpha < \dfrac{\mathrm{\pi }}{3}) $ .
由 $ 0 < \alpha < \dfrac{\mathrm{\pi }}{3} $ ,得 $ \dfrac{\mathrm{\pi }}{6} < 2\alpha +\dfrac{\mathrm{\pi }}{6} < \dfrac{5\mathrm{\pi }}{6} $ ,则当 $ 2\alpha +\dfrac{\mathrm{\pi }}{6}=\dfrac{\mathrm{\pi }}{2} $ ,即 $ \alpha =\dfrac{\mathrm{\pi }}{6} $ 时, $ S(\alpha )_{ \max }=600\sqrt{3} $ ,
所以当 $ \alpha =\dfrac{\mathrm{\pi }}{6} $ 时, $ S(\alpha ) $ 取得最大值,最大值为 $ 600\sqrt{3} $ 平方米.
解析:
二、刷能力
1.如图所示,一个以 $ OA $ 为始边, $ OB $ 为终边的单摆的角 $ \theta (-\mathrm{\pi } < \theta < \mathrm{\pi }) $ 与时间 $ t $ (单位: $ \mathrm{s} $ )满足函数关系式 $ \theta =\dfrac{1}{2} \sin (2t+\dfrac{\mathrm{\pi }}{2}) $ , $ t\in [0,+\mathrm{\infty }) $ ,则当 $ t=0\mathrm{s} $ 时,角 $ \theta $ 的大小及单摆频率是( )
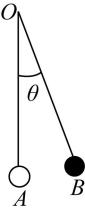
A. $ {\rm 2,} \dfrac{1}{\mathrm{\pi }} $
B. $ \dfrac{1}{2} $ , $ \dfrac{1}{\mathrm{\pi }} $
C. $ \dfrac{1}{2} $ , $ \mathrm{\pi } $
D. $ {\rm 2,} \mathrm{\pi } $
答案:B
解析:当 $ t=0\mathrm{s} $ 时, $ \theta =\dfrac{1}{2} \sin \dfrac{\mathrm{\pi }}{2}=\dfrac{1}{2} $ ,由函数解析式易知单摆周期为 $ \dfrac{2\mathrm{\pi }}{2}=\mathrm{\pi } $ ,故单摆频率为 $ \dfrac{1}{\mathrm{\pi }} $ .
2.如图,质点 $ P $ 在以坐标原点 $ O $ 为圆心,半径为1的圆上逆时针做匀速圆周运动,质点 $ P $ 运动的角速度大小为 $ 2\mathrm{r}\mathrm{a}\mathrm{d}/\mathrm{s} $ ,起点 $ {P}_{0} $ 为射线 $ y=-x(x\geqslant 0) $ 与 $ \odot O $ 的交点.则当 $ 0\leqslant t\leqslant 12 $ 时,下列选项中,是动点 $ P $ 的纵坐标 $ y $ 关于时间 $ t $ (单位: $ \mathrm{s} $ )的函数的单调递增区间的是( )
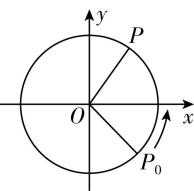
A. $ [0,\dfrac{\mathrm{\pi }}{2}] $
B. $ [\dfrac{7\mathrm{\pi }}{8},\dfrac{11\mathrm{\pi }}{8}] $
C. $ [\dfrac{11\mathrm{\pi }}{8},\dfrac{15\mathrm{\pi }}{8}] $
D. $ [\dfrac{3\mathrm{\pi }}{4},\dfrac{11\mathrm{\pi }}{4}] $
答案:B
解析:由题意,设 $ y=A \sin (\omega t+\varphi ) $ ,因为质点 $ P $ 在单位圆上运动的角速度大小为 $ 2\mathrm{r}\mathrm{a}\mathrm{d}/\mathrm{s} $ ,起点 $ {P}_{0} $ 为射线 $ y=-x(x\geqslant 0) $ 与 $ \odot O $ 的交点,
所以 $ A=1 $ , $ \omega =2 $ , $ \varphi =-\dfrac{\mathrm{\pi }}{4} $ ,所以动点 $ P $ 的纵坐标 $ y $ 关于时间 $ t $ (单位: $ \mathrm{s} $ )的函数解析式为 $ y= \sin (2t-\dfrac{\mathrm{\pi }}{4}) $ .
由 $ -\dfrac{\mathrm{\pi }}{2}+2k\mathrm{\pi }\leqslant 2t-\dfrac{\mathrm{\pi }}{4}\leqslant \dfrac{\mathrm{\pi }}{2}+2k\mathrm{\pi } $ , $ k\in \boldsymbol{Z} $ ,得 $ -\dfrac{\mathrm{\pi }}{8}+k\mathrm{\pi }\leqslant t\leqslant \dfrac{3\mathrm{\pi }}{8}+k\mathrm{\pi } $ , $ k\in \boldsymbol{Z} $ .
又 $ 0\leqslant t\leqslant 12 $ ,所以 $ 0\leqslant t\leqslant \dfrac{3\mathrm{\pi }}{8} $ , $ \dfrac{7\mathrm{\pi }}{8}\leqslant t\leqslant \dfrac{11\mathrm{\pi }}{8} $ , $ \dfrac{15\mathrm{\pi }}{8}\leqslant t\leqslant \dfrac{19\mathrm{\pi }}{8} $ , $ \dfrac{23\mathrm{\pi }}{8}\leqslant t\leqslant \dfrac{27\mathrm{\pi }}{8} $ .
所以动点 $ P $ 的纵坐标 $ y $ 关于时间 $ t $ (单位: $ \mathrm{s} $ )的函数的单调递增区间为 $ [0,\dfrac{3\mathrm{\pi }}{8}] $ , $ [\dfrac{7\mathrm{\pi }}{8},\dfrac{11\mathrm{\pi }}{8}] $ , $ [\dfrac{15\mathrm{\pi }}{8},\dfrac{19\mathrm{\pi }}{8}] $ , $ [\dfrac{23\mathrm{\pi }}{8},\dfrac{27\mathrm{\pi }}{8}] $ .故选 $ \mathrm{B} $ .
3.为了研究钟表与三角函数的关系,建立如图所示的坐标系,设秒针针尖位置为 $ P(x,y) $ .若初始位置为 $ {P}_{0}(\dfrac{\sqrt{3}}{2},\dfrac{1}{2}) $ ,当秒针针尖从 $ {P}_{0} $ (注:此时 $ t=0 $ )正常开始走时,点 $ P $ 的纵坐标 $ y $ 与时间 $ t $ (单位:秒)的函数关系式为( )
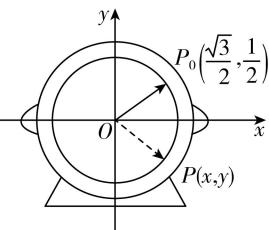
A. $ y= \sin (\dfrac{\mathrm{\pi }}{30}t+\dfrac{\mathrm{\pi }}{6})(t\geqslant 0) $
B. $ y= \sin (-\dfrac{\mathrm{\pi }}{60}t-\dfrac{\mathrm{\pi }}{6})(t\geqslant 0) $
C. $ y= \sin (-\dfrac{\mathrm{\pi }}{30}t+\dfrac{\mathrm{\pi }}{6})(t\geqslant 0) $
D. $ y= \sin (-\dfrac{\mathrm{\pi }}{30}t+\dfrac{\mathrm{\pi }}{3})(t\geqslant 0) $
答案:C
解析:根据题意,设 $ y=A \sin (\omega t+\varphi )(A > 0,\omega < 0,-\mathrm{\pi }\leqslant \varphi < \mathrm{\pi }) $ ,
由题意可知,初相 $ \varphi $ 为第一象限角,且 $ \begin{cases} \cos \varphi =\dfrac{\sqrt{3}}{2},\\ \sin \varphi =\dfrac{1}{2},\end{cases} $ 又因为 $ -\mathrm{\pi }\leqslant \varphi < \mathrm{\pi } $ ,则 $ \varphi =\dfrac{\mathrm{\pi }}{6} $ , $ A=\sqrt{{\left(\dfrac{\sqrt{3}}{2}\right) ^ {2}}+{\left(\dfrac{1}{2}\right) ^ {2}}}=1 $ ,
函数 $ y= \sin (\omega t+\dfrac{\mathrm{\pi }}{6})(\omega < 0) $ 的最小正周期 $ T=60 $ ,
所以 $ \omega =-\dfrac{2\mathrm{\pi }}{T}=-\dfrac{2\mathrm{\pi }}{60}=-\dfrac{\mathrm{\pi }}{30} $ ,
所以点 $ P $ 的纵坐标 $ y $ 与时间 $ t $ 的函数关系式为 $ y= \sin (-\dfrac{\mathrm{\pi }}{30}t+\dfrac{\mathrm{\pi }}{6})(t\geqslant 0) $ .故选 $ \mathrm{C} $ .
4.音乐喷泉曲线形似藤蔓上挂结的葫芦,也可称为葫芦曲线,它的性质是每经过相同的时间间隔,它的振幅就变化一次.如图所示,某一条葫芦曲线对应的方程为 $ |y|=(2-\dfrac{1}{2}[\dfrac{2x}{\mathrm{\pi }}])| \sin \omega x| $ , $ x\geqslant 0 $ , $ \omega \in (1,3) $ ,其中 $ [x] $ 表示不超过 $ x $ 的最大整数.若该曲线还满足经过点 $ M(\dfrac{3}{4}\mathrm{\pi },\dfrac{3}{2}) $ ,则该葫芦曲线与直线 $ x=\dfrac{7}{6}\mathrm{\pi } $ 交点的纵坐标为( )
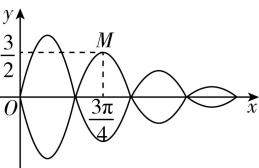
A. $ ±\dfrac{1}{2} $
B. $ ±\dfrac{\sqrt{2}}{2} $
C. $ ±\dfrac{\sqrt{3}}{2} $
D. $ ±1 $
答案:C
解析:将点 $ M(\dfrac{3}{4}\mathrm{\pi },\dfrac{3}{2}) $ 的坐标代入方程可得 $ (2-\dfrac{1}{2}[\dfrac{3}{2}])| \sin \dfrac{3\mathrm{\pi }}{4}\omega |=\dfrac{3}{2} $ ,
即 $ | \sin \dfrac{3\mathrm{\pi }}{4}\omega |=1 $ ,由 $ \omega \in (1,3) $ ,可得 $ \omega =2 $ ,
因此曲线方程为 $ |y|=(2-\dfrac{1}{2}[\dfrac{2x}{\mathrm{\pi }}])| \sin 2x| $ .
当 $ x=\dfrac{7}{6}\mathrm{\pi } $ 时,可得 $ |y|=(2-\dfrac{1}{2}[\dfrac{2×\dfrac{7}{6}\mathrm{\pi }}{\mathrm{\pi }}])| \sin 2×\dfrac{7}{6}\mathrm{\pi }|=(2-\dfrac{1}{2}[\dfrac{7}{3}])| \sin \dfrac{7}{3}\mathrm{\pi }|=| \sin \dfrac{\mathrm{\pi }}{3}|=\dfrac{\sqrt{3}}{2} $ ,
所以交点的纵坐标为 $ ±\dfrac{\sqrt{3}}{2} $ .故选 $ \mathrm{C} $ .
5.(多选)从出生之日起,人的体力、情绪、智力呈周期性变化,假设在前30天内,它们的变化规律如图所示(均为可向右无限延伸的正弦型曲线模型):
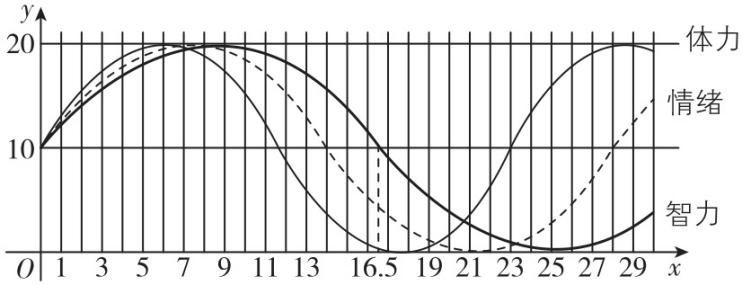
记智力曲线为 $ I $ ,情绪曲线为 $ E $ ,体力曲线为 $ P $ ,且三条曲线的起点位于坐标系的同一点处,则( )(多选)
A.体力曲线 $ P $ 的最小正周期是三条曲线中最小的
B.第462天时,智力曲线 $ I $ 与情绪曲线 $ E $ 都处于上升期
C.智力、情绪、体力三条曲线存在无数个公共点
D.不存在正整数 $ n $ ,使得第 $ n $ 天时,智力、情绪、体力三条曲线同时处于最高点或最低点
答案:ACD
解析:对于 $ \mathrm{A} $ ,观察题图可知,智力曲线 $ I $ 的最小正周期 $ {T}_{1}=33 $ ,情绪曲线 $ E $ 的最小正周期 $ {T}_{2}=28 $ ,体力曲线 $ P $ 的最小正周期 $ {T}_{3}=23 $ ,因此体力曲线 $ P $ 的最小正周期是三条曲线中最小的, $ \mathrm{A} $ 正确;
对于 $ \mathrm{B} {\rm ,462} $ 除以33的余数为0,462除以28的余数为14,此时情绪曲线 $ E $ 处于下降期,而智力曲线 $ I $ 刚好处于上升期, $ \mathrm{B} $ 错误;
对于 $ \mathrm{C} $ ,智力曲线 $ I $ 的对称中心的横坐标 $ {x}_{1}=16.5{k}_{1} $ , $ {k}_{1}\in \boldsymbol{N} $ ,情绪曲线 $ E $ 的对称中心的横坐标 $ {x}_{2}=14{k}_{2} $ , $ {k}_{2}\in \boldsymbol{N} $ ,体力曲线 $ P $ 的对称中心的横坐标 $ {x}_{3}=11.5{k}_{3} $ , $ {k}_{3}\in \boldsymbol{N} $ ,取 $ 16.5 {\rm ,14} $ , $ 11.5 $ 的公倍数即得3条曲线公共对称中心的横坐标,有无数个,即三条曲线存在无数个公共的对称中心,因此智力、情绪、体力三条曲线存在无数个公共点, $ \mathrm{C} $ 正确;
对于 $ \mathrm{D} $ ,智力曲线 $ I $ 的对称轴方程 $ {t}_{1}=8.25+16.5{n}_{1} $ , $ {n}_{1}\in \boldsymbol{N} $ ,情绪曲线 $ E $ 的对称轴方程 $ {t}_{2}=7+14{n}_{2} $ , $ {n}_{2}\in \boldsymbol{N} $ ,体力曲线 $ P $ 的对称轴方程 $ {t}_{3}=5.75+11.5{n}_{3} $ , $ {n}_{3}\in \boldsymbol{N} $ ,令 $ 8.25+16.5{n}_{1}=7+14{n}_{2}=5.75+11.5{n}_{3} $ ,
由 $ 8.25+16.5{n}_{1}=7+14{n}_{2} $ ,得 $ 165{n}_{1}-140{n}_{2}=-12.5 $ ,而 $ 165{n}_{1} $ , $ 140{n}_{2}\in \boldsymbol{N} $ , $ -12.5\notin \mathrm{Z} $ ,
因此不存在自然数使得方程 $ 8.25+16.5{n}_{1}=7+14{n}_{2} $ 成立,即智力曲线和情绪曲线没有公共的对称轴,同理三条曲线不存在公共的对称轴,
因此不存在正整数 $ n $ ,使得第 $ n $ 天时,智力、情绪、体力三条曲线同时处于最高点或最低点, $ \mathrm{D} $ 正确.故选 $ \mathrm{A}\mathrm{C}\mathrm{D} $ .
6.摩天轮是一种大型转轮状的机械游乐设施,游客坐在摩天轮的座舱里可从高处俯瞰四周景色.如图,某摩天轮最高点距离地面高度为 $ 120\mathrm{m} $ ,转盘直径为 $ 110\mathrm{m} $ ,均匀设置有48个座舱(按顺时针依次编号为1至48号),开启后按逆时针方向匀速旋转,游客在座舱转到距离地面最近的位置进舱,转一周需要 $ 30 \min $ .甲、乙两户家庭去坐摩天轮,甲家庭先坐上了1号座舱,乙家庭坐上了 $ k $ 号座舱,若从乙家庭坐进座舱开始计时, $ 10 \min $ 内(含 $ 10 \min $ )出现了两户家庭的座舱离地面高度一样的情况,则 $ k $ 的最小值是.

解析:设乙家庭坐进座舱后转动 $ t \min $ 出现了两户家庭的座舱离地面高度一样的情况, $ 0 < t\leqslant 10 $ ,只需考虑旋转的第一周即可.
摩天轮的座舱每分钟转动 $ \dfrac{2\mathrm{\pi }}{30}=\dfrac{\mathrm{\pi }}{15} $ ,则乙家庭的座舱 $ t \min $ 转过的弧度数为 $ \dfrac{\mathrm{\pi }}{15}t $ ,
摩天轮的两个相邻座舱中间的圆弧所对的圆心角为 $ \dfrac{2\mathrm{\pi }}{48}=\dfrac{\mathrm{\pi }}{24} $ ,此时甲家庭的座舱转过的弧度数为 $ \dfrac{(k-1)\mathrm{\pi }}{24}+\dfrac{\mathrm{\pi }}{15}t $ .
因为 $ t \min $ 时,甲、乙两户家庭的座舱关于摩天轮垂直于地面的轴对称,所以 $ \dfrac{(k-1)\mathrm{\pi }}{24}+\dfrac{\mathrm{\pi }}{15}t+\dfrac{\mathrm{\pi }}{15}t=2\mathrm{\pi } $ ,
整理得 $ k=48-\dfrac{16}{5}t+1\geqslant 17 $ ,当且仅当 $ t=10 $ 时取等号,
所以 $ k $ 的最小值是17.
7.主动降噪耳机工作的原理是先通过微型麦克风采集周围的噪声,然后降噪芯片生成与噪声振幅相同、相位相反的声波来抵消噪声(如图所示).已知某噪声声波曲线 $ f(x)=A \sin (\dfrac{2\mathrm{\pi }}{3}x+\varphi )(A > 0,0\leqslant \varphi < \mathrm{\pi }) $ ,其振幅为2,且经过点 $ (1,-2) $ .
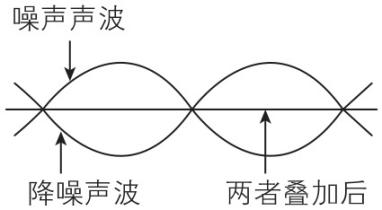
(1) 求该噪声声波曲线 $ f(x) $ 的解析式以及降噪芯片生成的降噪声波曲线 $ g(x) $ 的解析式;
(2) 证明: $ g(x)+g(x+1)+g(x+2) $ 为定值.
答案:(1) 【解】由振幅为 $ {\rm 2,} A > 0 $ ,可得 $ A=2 $ , $ f(x)=2 \sin (\dfrac{2\mathrm{\pi }}{3}x+\varphi ) $ ,
由噪声声波曲线经过点 $ (1,-2) $ ,得 $ -2=2 \sin (\dfrac{2\mathrm{\pi }}{3}+\varphi )⇒ \sin (\dfrac{2\mathrm{\pi }}{3}+\varphi )=-1 $ ,
而 $ 0\leqslant \varphi < \mathrm{\pi } $ , $ \dfrac{2\mathrm{\pi }}{3}+\varphi \in [\dfrac{2\mathrm{\pi }}{3},\dfrac{5\mathrm{\pi }}{3}) $ ,
则 $ \dfrac{2\mathrm{\pi }}{3}+\varphi =\dfrac{3\mathrm{\pi }}{2}⇒\varphi =\dfrac{5\mathrm{\pi }}{6} $ ,
则 $ f(x)=2 \sin (\dfrac{2\mathrm{\pi }}{3}x+\dfrac{5\mathrm{\pi }}{6}) $ .
又降噪声波曲线与噪声声波曲线的振幅相同、相位相反,
所以 $ g(x)=-2 \sin (\dfrac{2\mathrm{\pi }}{3}x+\dfrac{5\mathrm{\pi }}{6}) $ .
(2) 【证明】由 $ (1)g(x)=-2 \sin (\dfrac{2\mathrm{\pi }}{3}x+\dfrac{5\mathrm{\pi }}{6}) $
$ =-2 \sin (\dfrac{2\mathrm{\pi }}{3}x+\dfrac{\mathrm{\pi }}{3}+\dfrac{\mathrm{\pi }}{2}) $
$ =-2 \cos (\dfrac{2\mathrm{\pi }}{3}x+\dfrac{\mathrm{\pi }}{3}) $ ,
则 $ g(x)+g(x+1)+g(x+2) $
$ =-2 \cos (\dfrac{2\mathrm{\pi }}{3}x+\dfrac{\mathrm{\pi }}{3})-2 \cos (\dfrac{2\mathrm{\pi }}{3}x+\mathrm{\pi })-2 \cos (\dfrac{2\mathrm{\pi }}{3}x+\dfrac{2\mathrm{\pi }}{3}+\mathrm{\pi }) $
$ =-2 \cos (\dfrac{2\mathrm{\pi }}{3}x+\dfrac{\mathrm{\pi }}{3})+2 \cos \dfrac{2\mathrm{\pi }x}{3}+2 \cos (\dfrac{2\mathrm{\pi }}{3}x+\dfrac{2\mathrm{\pi }}{3}) $
$ =-2( \cos \dfrac{2\mathrm{\pi }x}{3}\cdot \dfrac{1}{2}- \sin \dfrac{2\mathrm{\pi }x}{3}\cdot \dfrac{\sqrt{3}}{2})+2 \cos \dfrac{2\mathrm{\pi }x}{3}+2[ \cos \dfrac{2\mathrm{\pi }x}{3}\cdot (-\dfrac{1}{2})- \sin \dfrac{2\mathrm{\pi }x}{3}\cdot \dfrac{\sqrt{3}}{2}] $
$ =- \cos \dfrac{2\mathrm{\pi }x}{3}+\sqrt{3} \sin \dfrac{2\mathrm{\pi }x}{3}+2 \cos \dfrac{2\mathrm{\pi }x}{3}- \cos \dfrac{2\mathrm{\pi }x}{3}-\sqrt{3} \sin \dfrac{2\mathrm{\pi }x}{3}=0 $ ,
即 $ g(x)+g(x+1)+g(x+2) $ 为定值0.
解析:
8.近年来,我国逐渐用风能等清洁能源替代传统能源,目前利用风能发电的主要手段是风车发电.如图,风车由一座塔和三个叶片组成,每两个叶片之间的夹角均为 $ \dfrac{2\mathrm{\pi }}{3} $ ,现有一个风车,塔高100米,叶片长40米.叶片按照逆时针方向匀速转动,并且每5秒旋转一圈,风车开始旋转时某叶片的一个端点 $ P $ 在风车的最低点(此时 $ P $ 离地面60米).设点 $ P $ 转动 $ t $ (秒)后离地面的距离为 $ S $ (米),则 $ S $ 关于 $ t $ 的函数关系式为 $ S(t)=A \sin (\omega t+\varphi )+B(A > 0,\omega > 0,|\varphi | < \mathrm{\pi }) $ .

(1) 求 $ S(t) $ 的解析式;
(2) 求叶片旋转一圈内点 $ P $ 离地面的高度不低于80米的时长.
答案:(1) 【解】以风车塔底为坐标原点建立如图所示平面直角坐标系,
当 $ t=0 $ 时,风车开始旋转时某叶片的一个端点 $ P $ 在风车的最低点,设为 $ {P}_{0} $ ,则 $ {P}_{0}(0,60) $ ,
由题意得 $ \omega =\dfrac{2\mathrm{\pi }}{5} $ ,
且 $ \begin{cases}A+B=100+40,\\ -A+B=100-40,\\ S(0)=A \sin \varphi +B=60,\end{cases} $
解得 $ \begin{cases}A=40,\\ B=100,\\ \varphi =-\dfrac{\mathrm{\pi }}{2},\end{cases} $
所以 $ S(t)=40 \sin (\dfrac{2\mathrm{\pi }}{5}t-\dfrac{\mathrm{\pi }}{2})+100 $ , $ t\in [0,+\mathrm{\infty }) $ .

(2) 【解】令 $ S(t)\geqslant 80 $ ,
则 $ S(t)=40 \sin (\dfrac{2\mathrm{\pi }}{5}t-\dfrac{\mathrm{\pi }}{2})+100\geqslant 80 $ ,
即 $ \cos \dfrac{2\mathrm{\pi }}{5}t\leqslant \dfrac{1}{2} $ ,
所以 $ 2k\mathrm{\pi }+\dfrac{\mathrm{\pi }}{3}\leqslant \dfrac{2\mathrm{\pi }}{5}t\leqslant 2k\mathrm{\pi }+\dfrac{5\mathrm{\pi }}{3}(k\in \boldsymbol{Z}) $ ,
解得 $ \dfrac{5}{6}+5k\leqslant t\leqslant \dfrac{25}{6}+5k(k\in \boldsymbol{Z}) $ .
当 $ k=0 $ 时, $ \dfrac{5}{6}\leqslant t\leqslant \dfrac{25}{6} $ , $ \dfrac{25}{6}-\dfrac{5}{6}=\dfrac{10}{3} $ ,
所以叶片旋转一圈内点 $ P $ 离地面的高度不低于80米的时长为 $ \dfrac{10}{3} $ 秒.
解析:
9.如图所示的图象显示的是相对平均海平面的某海湾的水面高度 $ y $ (单位: $ \mathrm{m} $ )在某天24小时内的变化情况,则水面高度 $ y $ 关于从夜间0时开始的时间 $ x $ (单位:时)的函数关系式为 , $ x\in [0,24] $ .
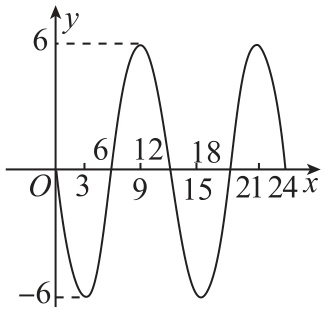
答案: $ y=-6 \sin \text{ }\dfrac{\mathrm{\pi }}{6}x $
解析:将其看成 $ y=A \sin (\omega x+\varphi )(A > 0,\omega > 0) $ 的图象,
由图象知 $ A=6 $ , $ T=12 $ , $ \therefore \omega =\dfrac{2\mathrm{\pi }}{T}=\dfrac{\mathrm{\pi }}{6} $ .
将 $ (6,0) $ 看成函数图象的第一个特殊点,则 $ \dfrac{\mathrm{\pi }}{6}×6+\varphi =0 $ ,得 $ \varphi =-\mathrm{\pi } $ , $ \therefore $ 函数关系式为 $ y=6 \sin (\dfrac{\mathrm{\pi }}{6}x-\mathrm{\pi })=-6 \sin \text{ }\dfrac{\mathrm{\pi }}{6}x. $
10.某地为发展旅游事业,在旅游手册中给出了当地一年12个月每个月的平均气温 $ y $ (单位: $ \mathrm{℃} $ ),如图所示.根据图中提供的数据,试用 $ y=A \sin (\omega x+\varphi )+b(A > 0,\omega > 0,-\mathrm{\pi } < \varphi < 0) $ 近似地拟合出月平均气温 $ y $ 与时间 $ x $ (单位:月)的函数关系式为 , $ x=1 {\rm ,2} $ , $ \cdots $ ,12.
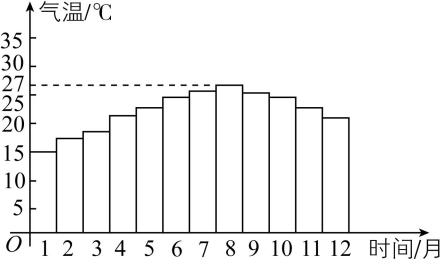
答案: $ y=6 \sin (\dfrac{\mathrm{\pi }}{7}x-\dfrac{9\mathrm{\pi }}{14})+21 $
解析:若以1月份为最低气温,8月份为最高气温,则可得 $ A=\dfrac{27-15}{2}=6 $ , $ b=\dfrac{27+15}{2}=21 $ , $ T=(8-1)×2=14 $ ,所以 $ \omega =\dfrac{2\mathrm{\pi }}{T}=\dfrac{\mathrm{\pi }}{7} $ ,所以 $ y=6 \sin (\dfrac{\mathrm{\pi }}{7}x+\varphi )+21 $ .将点 $ (1,15) $ , $ (8,27) $ 的坐标分别代入,
可得 $ \begin{cases}6 \sin \left(\dfrac{\mathrm{\pi }}{7}+\varphi \right)+21=15,\\ 6 \sin \left(\dfrac{8\mathrm{\pi }}{7}+\varphi \right)+21=27,\end{cases} $
两式相减得 $ \sin (\dfrac{\mathrm{\pi }}{7}+\varphi )- \sin (\dfrac{8\mathrm{\pi }}{7}+\varphi )=-2 $ ,
即 $ \sin (\dfrac{\mathrm{\pi }}{7}+\varphi )+ \sin (\dfrac{\mathrm{\pi }}{7}+\varphi )=-2 $ ,
即 $ \sin (\dfrac{\mathrm{\pi }}{7}+\varphi )=-1 $ ,所以 $ \dfrac{\mathrm{\pi }}{7}+\varphi =-\dfrac{\mathrm{\pi }}{2}+2k\mathrm{\pi } $ , $ k\in \boldsymbol{Z} $ ,则 $ \varphi =-\dfrac{9\mathrm{\pi }}{14}+2k\mathrm{\pi } $ , $ k\in \boldsymbol{Z} $ .
又 $ -\mathrm{\pi } < \varphi < 0 $ ,所以 $ \varphi =-\dfrac{9\mathrm{\pi }}{14} $ ,
所以函数解析式为 $ y=6 \sin (\dfrac{\mathrm{\pi }}{7}x-\dfrac{9\mathrm{\pi }}{14})+21 $ , $ x=1 {\rm ,2} $ , $ \cdots $ ,12.



 (多选)
(多选) (多选)
(多选)










