第五章高考强化
一、刷真题
1.在平面直角坐标系 $ xOy $ 中,角 $ \alpha $ 与角 $ \beta $ 均以 $ Ox $ 为始边,它们的终边关于原点对称.若 $ \alpha \in [\dfrac{\mathrm{\pi }}{6},\dfrac{\mathrm{\pi }}{3}] $ ,则 $ \cos \beta $ 的最大值为 .
解析: $ \because \alpha \in [\dfrac{\mathrm{\pi }}{6},\dfrac{\mathrm{\pi }}{3}] $ , $ \therefore \cos \dfrac{\mathrm{\pi }}{3}\leqslant \cos \alpha \leqslant \cos \dfrac{\mathrm{\pi }}{6} $ ,即 $ \dfrac{1}{2}\leqslant \cos \alpha \leqslant \dfrac{\sqrt{3}}{2} $ .又 $ \beta -\alpha =\mathrm{\pi }+2k\mathrm{\pi } $ , $ k\in \mathbf{Z} $ , $ \therefore \cos \beta = \cos (\alpha +\mathrm{\pi }+2k\mathrm{\pi })= \cos (\alpha +\mathrm{\pi })=- \cos \alpha $ , $ k\in \mathbf{Z} $ , $ \therefore -\dfrac{\sqrt{3}}{2}\leqslant \cos \beta \leqslant -\dfrac{1}{2} $ , $ \therefore \cos \beta $ 的最大值为 $ -\dfrac{1}{2} $ .
2.若 $ \theta \in (0,\dfrac{\mathrm{\pi }}{2}) $ , $ \tan \theta =\dfrac{1}{3} $ ,则 $ \sin \theta - \cos \theta = $ .
答案: $ -\dfrac{\sqrt{10}}{5} $
解析:因为 $ \theta \in (0,\dfrac{\mathrm{\pi }}{2}) $ , $ \tan \theta =\dfrac{ \sin \theta }{ \cos \theta }=\dfrac{1}{3} $ ,所以 $ \cos \theta =3 \sin \theta . $ 又因为 $ { \cos }^{2}\theta +{ \sin }^{2}\theta =1 $ ,解得 $ \sin \hat{}2\theta =\dfrac{1}{10} $ ,即 $ \sin \theta =\dfrac{\sqrt{10}}{10} $ , $ \cos \theta =\dfrac{3\sqrt{10}}{10} $ ,所以 $ \sin \theta - \cos \theta =-\dfrac{\sqrt{10}}{5} $ .
3.已知 $ \cos (\alpha +\beta )=m $ , $ \tan \alpha \tan \beta =2 $ ,则 $ \cos (\alpha -\beta )= $ ( )
A. $ -3m $
B. $ -\dfrac{m}{3} $
C. $ \dfrac{m}{3} $
D. $ 3m $
答案:A
解析:由 $ \tan \alpha \tan \beta =2 $ ,可得 $ \dfrac{ \sin \alpha \sin \beta }{ \cos \alpha \cos \beta }=2 $ ,即 $ \sin \alpha \sin \beta =2 \cos \alpha \cos \beta $ .由 $ \cos (\alpha +\beta )= \cos \alpha \cos \beta - \sin \alpha \sin \beta =m $ ,可得 $ \cos \alpha \cos \beta =-m $ , $ \sin \alpha \sin \beta =-2m $ ,所以 $ \cos (\alpha -\beta )= \cos \alpha \cos \beta + \sin \alpha \sin \beta =-3m $ ,故选 $ \mathrm{A} $ .
4.已知 $ \dfrac{ \cos \alpha }{ \cos \alpha - \sin \alpha }=\sqrt{3} $ ,则 $ \tan (\alpha +\dfrac{\mathrm{\pi }}{4})= $ ( )
A. $ 2\sqrt{3}+1 $
B. $ 2\sqrt{3}-1 $
C. $ \dfrac{\sqrt{3}}{2} $
D. $ 1-\sqrt{3} $
答案:B
解析: $ \because \dfrac{ \cos \alpha }{ \cos \alpha - \sin \alpha }=\dfrac{1}{1- \tan \alpha }=\sqrt{3} $ , $ \therefore \tan \alpha =1-\dfrac{\sqrt{3}}{3} $ ,
$ \therefore \tan (\alpha +\dfrac{\mathrm{\pi }}{4})=\dfrac{ \tan \alpha + \tan \dfrac{\mathrm{\pi }}{4}}{1- \tan \alpha \tan \dfrac{\mathrm{\pi }}{4}}=\dfrac{1-\dfrac{\sqrt{3}}{3}+1}{1-(1-\dfrac{\sqrt{3}}{3})}=2\sqrt{3}-1 $ ,故选 $ \mathrm{B} $ .
5.已知 $ \sin (\alpha -\beta )=\dfrac{1}{3} $ , $ \cos \alpha \sin \beta =\dfrac{1}{6} $ ,则 $ \cos (2\alpha +2\beta )= $ ( )
A. $ \dfrac{7}{9} $
B. $ \dfrac{1}{9} $
C. $ -\dfrac{1}{9} $
D. $ -\dfrac{7}{9} $
答案:B
解析: $ \because \sin (\alpha -\beta )= \sin \alpha \cos \beta - \cos \alpha \sin \beta =\dfrac{1}{3} $ , $ \cos \alpha \sin \beta =\dfrac{1}{6} $ , $ \therefore \sin \alpha \cos \beta =\dfrac{1}{3}+ \cos \alpha \sin \beta =\dfrac{1}{3}+\dfrac{1}{6}=\dfrac{1}{2} $ .
$ \therefore \sin (\alpha +\beta )= \sin \alpha \cos \beta + \cos \alpha \sin \beta =\dfrac{1}{2}+\dfrac{1}{6}=\dfrac{2}{3} $ , $ \therefore \cos (2\alpha +2\beta )= \cos [2(\alpha +\beta )]=1-2{ \sin }^{2}(\alpha +\beta )=1-2×{\left(\dfrac{2}{3}\right) ^ {2}}=\dfrac{1}{9} $ ,故选 $ \mathrm{B} $ .
6.若 $ \sin (\alpha +\beta )+ \cos (\alpha +\beta )=2\sqrt{2} \cos (\alpha +\dfrac{\mathrm{\pi }}{4}) \sin \text{ }\beta $ ,则( )
A. $ \tan (\alpha -\beta )=1 $
B. $ \tan (\alpha +\beta )=1 $
C. $ \tan (\alpha -\beta )=-1 $
D. $ \tan (\alpha +\beta )=-1 $
答案:C
解析:由已知等式,得 $ \sin \text{ }\alpha \cos \text{ }\beta + \sin \text{ }\beta \cos \text{ }\alpha + \cos \text{ }\alpha \cos \text{ }\beta - \sin \text{ }\alpha \sin \text{ }\beta =2\sqrt{2}×\dfrac{\sqrt{2}}{2}( \cos \text{ }\alpha - \sin \text{ }\alpha ) \sin \text{ }\beta $ ,整理得 $ \sin \text{ }\alpha \cos \text{ }\beta - \sin \text{ }\beta \cos \text{ }\alpha + \cos \text{ }\alpha \cos \text{ }\beta + \sin \text{ }\alpha \sin \text{ }\beta =0 $ ,即 $ \sin (\alpha -\beta )+ \cos (\alpha -\beta )=0 $ ,所以 $ \tan (\alpha -\beta )=-1 $ ,故选 $ \mathrm{C} $ .
7.若 $ \tan \theta =-2 $ ,则 $ \dfrac{ \sin \theta (1+ \sin 2\theta )}{ \sin \theta + \cos \theta }= $ ( )
A. $ -\dfrac{6}{5} $
B. $ -\dfrac{2}{5} $
C. $ \dfrac{2}{5} $
D. $ \dfrac{6}{5} $
答案:C
解析:因为 $ \dfrac{ \sin \theta (1+ \sin 2\theta )}{ \sin \theta + \cos \theta }=\dfrac{ \sin \theta ( \sin \theta + \cos \theta )^{2}}{ \sin \theta + \cos \theta }= \sin \theta ( \sin \theta + \cos \theta )=\dfrac{{ \sin }^{2}\theta + \sin \theta \cos \theta }{{ \sin }^{2}\theta +{ \cos }^{2}\theta }=\dfrac{\dfrac{{ \sin }^{2}\theta }{{ \cos }^{2}\theta }+\dfrac{ \sin \theta }{ \cos \theta }}{\dfrac{{ \sin }^{2}\theta }{{ \cos }^{2}\theta }+1}=\dfrac{{ \tan }^{2}\theta + \tan \theta }{{ \tan }^{2}\theta +1}=\dfrac{4-2}{4+1}=\dfrac{2}{5} $ ,故选 $ \mathrm{C} $ .
8.下列函数是偶函数的为( )
A. $ y=\dfrac{{\mathrm{e}}^{x}-{x}^{2}}{{\mathrm{e}}^{x}+{x}^{2}} $
B. $ y=\dfrac{ \cos x-{x}^{2}}{{x}^{2}+1} $
C. $ y=\dfrac{{\mathrm{e}}^{x}-x}{{\mathrm{e}}^{x}+x} $
D. $ y=\dfrac{ \sin x-x}{{x}^{2}+1} $
答案:B
解析:对于 $ \mathrm{A} $ ,记 $ f(x)=\dfrac{{\mathrm{e}}^{x}-{x}^{2}}{{\mathrm{e}}^{x}+{x}^{2}} $ ,定义域为 $ \boldsymbol{R} $ ,
则 $ f (-x )=\dfrac{{\mathrm{e}}^{-x}- (-x)^{2}}{{\mathrm{e}}^{-x}+ (-x)^{2}}=\dfrac{1-{x}^{2}{\mathrm{e}}^{x}}{1+{x}^{2}{\mathrm{e}}^{x}}\ne f (x ) $ ,则 $ f(x) $ 不是偶函数,故 $ \mathrm{A} $ 错误;
对于 $ \mathrm{B} $ ,记 $ g(x)=\dfrac{ \cos x-{x}^{2}}{{x}^{2}+1} $ ,定义域为 $ \boldsymbol{R} $ ,
则 $ g (-x )=\dfrac{ \cos (-x )- (-x)^{2}}{ (-x)^{2}+1}=\dfrac{ \cos x-{x}^{2}}{{x}^{2}+1}=g (x ) $ ,则 $ g(x) $ 是偶函数,故 $ \mathrm{B} $ 正确;
对于 $ \mathrm{C} $ ,记 $ ℎ(x)=\dfrac{{\mathrm{e}}^{x}-x}{{\mathrm{e}}^{x}+x} $ ,定义域为 $ \boldsymbol{R} $ ,则 $ ℎ(-x)=\dfrac{{\mathrm{e}}^{-x}-(-x)}{{\mathrm{e}}^{-x}+(-x)}=\dfrac{1+x{\mathrm{e}}^{x}}{1-x{\mathrm{e}}^{x}}\ne ℎ(x) $ ,则 $ ℎ(x) $ 不是偶函数,故 $ \mathrm{C} $ 错误;
对于 $ \mathrm{D} $ ,记 $ p(x)=\dfrac{ \sin x-x}{{x}^{2}+1} $ ,定义域为 $ \boldsymbol{R} $ ,
则 $ p (-x )=\dfrac{ \sin (-x )- (-x )}{ (-x)^{2}+1}=\dfrac{- \sin x+x}{{x}^{2}+1}=-p (x ) $ ,
则 $ p(x) $ 是奇函数,故 $ \mathrm{D} $ 错误,故选 $ \mathrm{B} $ .
9. 函数f(x)的图象关于直线x=2对称,且f(x)的一个周期为4,则f(x)的解析式可以是 ( )
$ {\rm \mathit{f}(\mathit{x})=sin} (\dfrac{\mathrm{\pi }}{2}x) $
$ {\rm \mathit{f}(\mathit{x})=cos} (\dfrac{\mathrm{\pi }}{2}x) $
$ {\rm \mathit{f}(\mathit{x})=sin} (\dfrac{\mathrm{\pi }}{4}x) $
$ {\rm \mathit{f}(\mathit{x})=cos} (\dfrac{\mathrm{\pi }}{4}x) $
答案:B
解析:各选项分析如下:
选项 | 解析式 | 对称轴 方程 | 周期 | 正误 |
A | f(x)=sin( $\dfrac{\pi }{2} {\rm \mathit{x}}$) | x=2k+1, k∈Z | 4 | × |
B | f(x)=cos( $\dfrac{\mathrm{\pi }}{2} {\rm \mathit{x}}$) | x=2k, k∈Z | 4 | √ |
C | f(x)=sin( $\dfrac{\mathrm{\pi }}{4} {\rm \mathit{x}}$) | x=4k+2, k∈Z | 8 | × |
D | f(x)=cos( $\dfrac{\mathrm{\pi }}{4} {\rm \mathit{x}}$) | x=4k, k∈Z | 8 | × |
故选B.
10.已知函数 $ f(x)=3 \sin (\omega x+\dfrac{\mathrm{\pi }}{3})(\omega > 0) $ 的最小正周期为 $ \mathrm{\pi } $ ,则 $ f(x) $ 在区间 $ [-\dfrac{\mathrm{\pi }}{12},\dfrac{\mathrm{\pi }}{6}] $ 上的最小值为( )
A. $ -\dfrac{3\sqrt{3}}{2} $
B. $ -\dfrac{3}{2} $
C.0
D. $ \dfrac{3}{2} $
答案:D
解析: $ \because f(x) $ 的最小正周期为 $ \mathrm{\pi } $ , $ \therefore \dfrac{2\mathrm{\pi }}{\omega }=\mathrm{\pi } $ ,得 $ \omega =2 $ , $ \therefore f(x)=3 \sin (2x+\dfrac{\mathrm{\pi }}{3}) $ .当 $ x\in [-\dfrac{\mathrm{\pi }}{12},\dfrac{\mathrm{\pi }}{6}] $ 时, $ 2x+\dfrac{\mathrm{\pi }}{3}\in [\dfrac{\mathrm{\pi }}{6},\dfrac{2\mathrm{\pi }}{3}] $ , $ \therefore f(x) $ 的最小值为 $ \dfrac{3}{2} $ ,故选 $ \mathrm{D} $ .
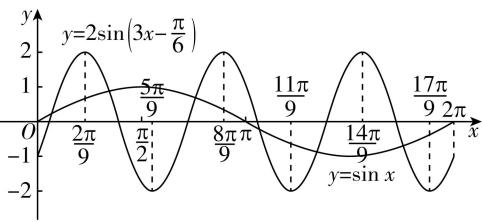
11.当 $ x\in [0,2\mathrm{\pi }] $ 时,曲线 $ y= \sin x $ 与 $ y=2 \sin (3x-\dfrac{\mathrm{\pi }}{6}) $ 的交点个数为( )
A.3
B.4
C.6
D.8
答案:C
解析:令 $ 3x-\dfrac{\mathrm{\pi }}{6}=\dfrac{\mathrm{\pi }}{2}+{k}_{1}\mathrm{\pi } $ , $ {k}_{1}\in \boldsymbol{Z} $ ,则 $ x=\dfrac{2\mathrm{\pi }}{9}+\dfrac{{k}_{1}\mathrm{\pi }}{3} $ , $ {k}_{1}\in \boldsymbol{Z} $ ,
又 $ x\in [0,2\mathrm{\pi }] $ ,所以 $ x=\dfrac{2\mathrm{\pi }}{9} $ , $ \dfrac{5\mathrm{\pi }}{9} $ , $ \dfrac{8\mathrm{\pi }}{9} $ , $ \dfrac{11\mathrm{\pi }}{9} $ , $ \dfrac{14\mathrm{\pi }}{9} $ , $ \dfrac{17\mathrm{\pi }}{9} $ .
令 $ 3x-\dfrac{\mathrm{\pi }}{6}={k}_{2}\mathrm{\pi } $ , $ {k}_{2}\in \boldsymbol{Z} $ ,则 $ x=\dfrac{\mathrm{\pi }}{18}+\dfrac{{k}_{2}\mathrm{\pi }}{3} $ , $ {k}_{2}\in \boldsymbol{Z} $ ,
又 $ x\in [0,2\mathrm{\pi }] $ ,所以 $ x=\dfrac{\mathrm{\pi }}{18} $ , $ \dfrac{7\mathrm{\pi }}{18} $ , $ \dfrac{13\mathrm{\pi }}{18} $ , $ \dfrac{19\mathrm{\pi }}{18} $ , $ \dfrac{25\mathrm{\pi }}{18} $ , $ \dfrac{31\mathrm{\pi }}{18} $ ,
如图,作出函数 $ y= \sin x $ 与 $ y=2 \sin (3x-\dfrac{\mathrm{\pi }}{6}) $ 在 $ [0,2\mathrm{\pi }] $ 上的大致图象,由图可知,两函数图象共有6个交点.故选 $ \mathrm{C} $ .
12.函数 $ y=f(x) $ 的图象由函数 $ y= \cos (2x+\dfrac{\mathrm{\pi }}{6}) $ 的图象向左平移 $ \dfrac{\mathrm{\pi }}{6} $ 个单位长度得到,则 $ y=f(x) $ 的图象与直线 $ y=\dfrac{1}{2}x-\dfrac{1}{2} $ 的交点个数为( )
A.1
B.2
C.3
D.4
答案:C
解析:由题意知 $ f(x)= \cos [2(x+\dfrac{\mathrm{\pi }}{6})+\dfrac{\mathrm{\pi }}{6}]= \cos (2x+\dfrac{\mathrm{\pi }}{2})=- \sin 2x $ ,画出函数 $ f(x) $ 的图象和直线 $ y=\dfrac{1}{2}x-\dfrac{1}{2} $ ,如图.
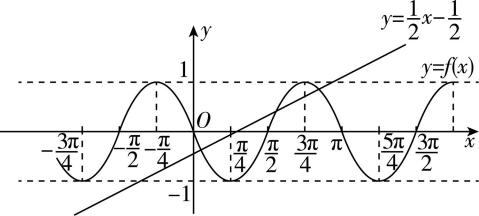
由图象可知,函数 $ y=f(x) $ 的图象与直线 $ y=\dfrac{1}{2}x-\dfrac{1}{2} $ 有3个交点,故选 $ \mathrm{C} $ .
13.已知函数 $ f(x)= \sin (\omega x+\varphi ) $ 在区间 $ (\dfrac{\mathrm{\pi }}{6},\dfrac{2\mathrm{\pi }}{3}) $ 单调递增,直线 $ x=\dfrac{\mathrm{\pi }}{6} $ 和 $ x=\dfrac{2\mathrm{\pi }}{3} $ 为函数 $ y=f(x) $ 的图象的两条对称轴,则 $ f(-\dfrac{5\mathrm{\pi }}{12})= $ ( )
A. $ -\dfrac{\sqrt{3}}{2} $
B. $ -\dfrac{1}{2} $
C. $ \dfrac{1}{2} $
D. $ \dfrac{\sqrt{3}}{2} $
答案:D
解析:由题意画出 $ f(x) $ 图象的简图(如图).
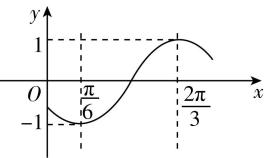
因为函数 $ f(x)= \sin (\omega x+\varphi ) $ 在区间 $ (\dfrac{\mathrm{\pi }}{6},\dfrac{2\mathrm{\pi }}{3}) $ 单调递增,且直线 $ x=\dfrac{\mathrm{\pi }}{6} $ 和直线 $ x=\dfrac{2\mathrm{\pi }}{3} $ 为函数 $ y=f(x) $ 的图象的两条对称轴,所以 $ \dfrac{2\mathrm{\pi }}{3}-\dfrac{\mathrm{\pi }}{6}=\dfrac{T}{2} $ , $ f(\dfrac{\mathrm{\pi }}{6})=-1 $ ,所以 $ T=\mathrm{\pi } $ ,即 $ |\omega |=\dfrac{2\mathrm{\pi }}{T}=2 $ ,则 $ \omega =2 $ 或 $ -2 $ .
而 $ f(\dfrac{\mathrm{\pi }}{6})=-1 $ ,即 $ \sin (2×\dfrac{\mathrm{\pi }}{6}+\varphi )=-1 $ 或 $ \sin (-2×\dfrac{\mathrm{\pi }}{6}+\varphi )=-1 $ ,所以 $ 2×\dfrac{\mathrm{\pi }}{6}+\varphi =-\dfrac{\mathrm{\pi }}{2}+2k\mathrm{\pi } $ 或 $ -2×\dfrac{\mathrm{\pi }}{6}+\varphi =-\dfrac{\mathrm{\pi }}{2}+2k\mathrm{\pi } $ , $ k\in \boldsymbol{Z} $ ,即 $ \varphi =-\dfrac{5\mathrm{\pi }}{6}+2k\mathrm{\pi } $ 或 $ -\dfrac{\mathrm{\pi }}{6}+2k\mathrm{\pi } $ , $ k\in \boldsymbol{Z} $ ,所以 $ f(x)= \sin (2x-\dfrac{5\mathrm{\pi }}{6}) $ 或 $ f(x)= \sin (-2x-\dfrac{\mathrm{\pi }}{6}) $ ,所以 $ f(-\dfrac{5\mathrm{\pi }}{12})= \sin (-\dfrac{5\mathrm{\pi }}{6}-\dfrac{5\mathrm{\pi }}{6})= \sin (-\dfrac{5\mathrm{\pi }}{3})= \sin \dfrac{\mathrm{\pi }}{3}=\dfrac{\sqrt{3}}{2} $ 或 $ f(-\dfrac{5\mathrm{\pi }}{12})= \sin (\dfrac{5\mathrm{\pi }}{6}-\dfrac{\mathrm{\pi }}{6})=\dfrac{\sqrt{3}}{2} $ ,故选 $ \mathrm{D} $ .
14.函数 $ y=-{x}^{2}+({\mathrm{e}}^{x}-{\mathrm{e}}^{-x}) \sin x $ 在区间 $ [-2.8,2.8] $ 的图象大致为( )
A.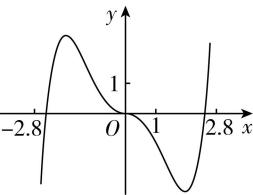
B.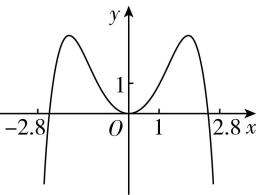
C.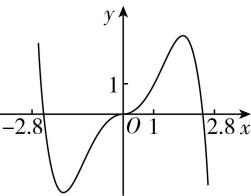
D.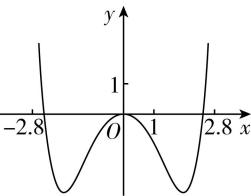
答案:B
解析:令函数 $ f(x)=-{x}^{2}+({\mathrm{e}}^{x}-{\mathrm{e}}^{-x})\cdot \sin x $ , $ x\in [-2.8,2.8] $ ,
因为 $ f(-x)=-{x}^{2}+({\mathrm{e}}^{-x}-{\mathrm{e}}^{x}) \sin (-x)=-{x}^{2}+({\mathrm{e}}^{x}-{\mathrm{e}}^{-x}) \sin x=f(x) $ ,
所以函数 $ y=f(x) $ 是偶函数,排除选项 $ \mathrm{A} $ , $ \mathrm{C} $ .
令 $ x=1 $ ,则 $ f(1)=-1+(\mathrm{e}-\dfrac{1}{\mathrm{e}}) \sin 1 $ .
因为 $ 1\in (\dfrac{\mathrm{\pi }}{4},\dfrac{\mathrm{\pi }}{3}) $ ,所以 $ \sin 1\in (\dfrac{\sqrt{2}}{2},\dfrac{\sqrt{3}}{2}) $ .
又 $ \mathrm{e}\approx 2.7 $ ,所以 $ \mathrm{e}-\dfrac{1}{\mathrm{e}} > 2 $ ,所以 $ (\mathrm{e}-\dfrac{1}{\mathrm{e}}) \sin 1 > \sqrt{2} $ ,
所以 $ f(1)=-1+(\mathrm{e}-\dfrac{1}{\mathrm{e}}) \sin 1 > 0 $ ,排除选项 $ \mathrm{D} $ ,故选 $ \mathrm{B} $ .
15.将函数 $ f(x)= \sin (\omega x+\dfrac{\mathrm{\pi }}{3})(\omega > 0) $ 的图象向左平移 $ \dfrac{\mathrm{\pi }}{2} $ 个单位长度后得到曲线 $ C $ ,若 $ C $ 关于 $ y $ 轴对称,则 $ \omega $ 的最小值是( )
A. $ \dfrac{1}{6} $
B. $ \dfrac{1}{4} $
C. $ \dfrac{1}{3} $
D. $ \dfrac{1}{2} $
答案:C
解析:将函数 $ f(x)= \sin (\omega x+\dfrac{\mathrm{\pi }}{3})(\omega > 0) $ 的图象向左平移 $ \dfrac{\mathrm{\pi }}{2} $ 个单位长度后得到曲线 $ C:f(x+\dfrac{\mathrm{\pi }}{2})= \sin [\omega (x+\dfrac{\mathrm{\pi }}{2})+\dfrac{\mathrm{\pi }}{3}]= \sin (\omega x+\dfrac{\omega \mathrm{\pi }}{2}+\dfrac{\mathrm{\pi }}{3}) $ .
由于曲线 $ C $ 关于 $ y $ 轴对称,则有 $ \dfrac{\omega \mathrm{\pi }}{2}+\dfrac{\mathrm{\pi }}{3}=k\mathrm{\pi }+\dfrac{\mathrm{\pi }}{2}(k\in \boldsymbol{Z}) $ ,
即 $ \omega =2k+\dfrac{1}{3}(k\in \boldsymbol{Z}) $ ,
又 $ \omega > 0 $ ,所以当 $ k=0 $ 时, $ \omega $ 取得最小值 $ \dfrac{1}{3} $ ,故选 $ \mathrm{C} $ .
16.(多选)[全国新课标Ⅱ $ 2024\cdot 9 {\rm ,6} $ 分]对于函数 $ f(x)= \sin 2x $ 和 $ g(x)= \sin (2x-\dfrac{\mathrm{\pi }}{4}) $ ,下列说法中正确的有( )(多选)
A. $ f(x) $ 与 $ g(x) $ 有相同的零点
B. $ f(x) $ 与 $ g(x) $ 有相同的最大值
C. $ f(x) $ 与 $ g(x) $ 有相同的最小正周期
D. $ f(x) $ 与 $ g(x) $ 的图象有相同的对称轴
答案:BC
解析:对于 $ \mathrm{A} $ ,令 $ f(x)=0 $ ,则 $ 2x={k}_{1}\mathrm{\pi }({k}_{1}\in \boldsymbol{Z}) $ ,解得 $ x=\dfrac{{k}_{1}\mathrm{\pi }}{2}({k}_{1}\in \boldsymbol{Z}) $ ,令 $ g(x)=0 $ ,则 $ 2x-\dfrac{\mathrm{\pi }}{4}={k}_{2}\mathrm{\pi }({k}_{2}\in \boldsymbol{Z}) $ ,解得 $ x=\dfrac{\mathrm{\pi }}{8}+\dfrac{{k}_{2}\mathrm{\pi }}{2}({k}_{2}\in \boldsymbol{Z}) $ ,因此 $ f(x) $ 与 $ g(x) $ 无相同零点,故 $ \mathrm{A} $ 错误;对于 $ \mathrm{B} $ , $ f(x) $ 与 $ g(x) $ 的最大值都为1,故 $ \mathrm{B} $ 正确;对于 $ \mathrm{C} $ , $ f(x) $ 与 $ g(x) $ 的最小正周期都是 $ \dfrac{2\mathrm{\pi }}{2}=\mathrm{\pi } $ ,故 $ \mathrm{C} $ 正确;对于 $ \mathrm{D} $ ,令 $ 2x=\dfrac{\mathrm{\pi }}{2}+{k}_{3}\mathrm{\pi }({k}_{3}\in \boldsymbol{Z}) $ ,得 $ x=\dfrac{\mathrm{\pi }}{4}+\dfrac{{k}_{3}\mathrm{\pi }}{2}({k}_{3}\in \boldsymbol{Z}) $ ,令 $ 2x-\dfrac{\mathrm{\pi }}{4}=\dfrac{\mathrm{\pi }}{2}+{k}_{4}\mathrm{\pi }({k}_{4}\in \boldsymbol{Z}) $ ,得 $ x=\dfrac{3}{8}\mathrm{\pi }+\dfrac{{k}_{4}\mathrm{\pi }}{2}({k}_{4}\in \boldsymbol{Z}) $ ,故 $ f(x) $ 与 $ g(x) $ 的图象无相同的对称轴,故 $ \mathrm{D} $ 错误.故选 $ \mathrm{B}\mathrm{C} $ .
17.把函数 $ y=f(x) $ 图象上所有点的横坐标缩短到原来的 $ \dfrac{1}{2} $ 倍,纵坐标不变,再把所得曲线向右平移 $ \dfrac{\mathrm{\pi }}{3} $ 个单位长度,得到函数 $ y= \sin (x-\dfrac{\mathrm{\pi }}{4}) $ 的图象,则 $ f(x)= $ ( )
A. $ \sin (\dfrac{x}{2}-\dfrac{7\mathrm{\pi }}{12}) $
B. $ \sin (\dfrac{x}{2}+\dfrac{\mathrm{\pi }}{12}) $
C. $ \sin (2x-\dfrac{7\mathrm{\pi }}{12}) $
D. $ \sin (2x+\dfrac{\mathrm{\pi }}{12}) $
答案:B
解析:将函数 $ y= \sin (x-\dfrac{\mathrm{\pi }}{4}) $ 的图象向左平移 $ \dfrac{\mathrm{\pi }}{3} $ 个单位长度得到函数 $ y= \sin [(x+\dfrac{\mathrm{\pi }}{3})-\dfrac{\mathrm{\pi }}{4}]= \sin (x+\dfrac{\mathrm{\pi }}{12}) $ 的图象,再将所得图象上所有点的横坐标伸长到原来的2倍,纵坐标不变,得到函数 $ f(x)= \sin (\dfrac{x}{2}+\dfrac{\mathrm{\pi }}{12}) $ 的图象.故选 $ \mathrm{B} $ .
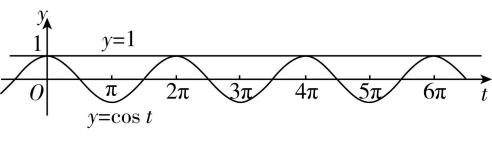
18.已知函数 $ f(x)= \cos \omega x-1(\omega > 0) $ 在区间 $ [0,2\mathrm{\pi }] $ 有且仅有3个零点,则 $ \omega $ 的取值范围是 .
解析:令 $ f(x)= \cos \omega x-1=0 $ ,得 $ \cos \omega x=1 $ ,又 $ x\in [0,2\mathrm{\pi }] $ ,则 $ \omega x\in [0,2\omega \mathrm{\pi }] $ ,令 $ t=\omega x\in [0,2\omega \mathrm{\pi }] $ ,因为 $ f(x) $ 在 $ [0,2\mathrm{\pi }] $ 有且仅有3个零点,所以 $ y= \cos t $ 的图象与直线 $ y=1 $ 在 $ [0,2\omega \mathrm{\pi }] $ 有且仅有3个交点,如图,所以 $ 4\mathrm{\pi }\leqslant 2\omega \mathrm{\pi } < 6\mathrm{\pi } $ ,解得
$ 2\leqslant \omega < 3 $ ,即 $ \omega $ 的取值范围是 $ [2,3) $ .
19.记函数 $ f(x)= \cos (\omega x+\varphi )(\omega > 0,0 < \varphi < \mathrm{\pi }) $ 的最小正周期为 $ T $ .若 $ f(T)=\dfrac{\sqrt{3}}{2} $ , $ x=\dfrac{\mathrm{\pi }}{9} $ 为 $ f(x) $ 的零点,则 $ \omega $ 的最小值为 .
解析:由已知得 $ f(T)=f(\dfrac{2\mathrm{\pi }}{\omega })= \cos (\omega \cdot \dfrac{2\mathrm{\pi }}{\omega }+\varphi )= \cos \varphi =\dfrac{\sqrt{3}}{2} $ .
又 $ 0 < \varphi < \mathrm{\pi } $ ,所以 $ \varphi =\dfrac{\mathrm{\pi }}{6} $ ,所以 $ f(x)= \cos (\omega x+\dfrac{\mathrm{\pi }}{6}) $ .
因为 $ x=\dfrac{\mathrm{\pi }}{9} $ 为 $ f(x) $ 的零点,所以 $ \dfrac{\mathrm{\pi }}{9}\omega +\dfrac{\mathrm{\pi }}{6}=\dfrac{\mathrm{\pi }}{2}+k\mathrm{\pi } $ , $ k\in \boldsymbol{Z} $ ,解得 $ \omega =9k+3 $ , $ k\in \boldsymbol{Z} $ .
又 $ \omega > 0 $ ,所以 $ \omega $ 的最小值为3.
20.已知函数 $ f(x)=2 \cos (\omega x+\varphi ) $ 的部分图象如图所示,则满足条件 $ (f(x)-f(-\dfrac{7\mathrm{\pi }}{4}))(f(x)-f(\dfrac{4\mathrm{\pi }}{3})) > 0 $ 的最小正整数 $ x $ 为 .
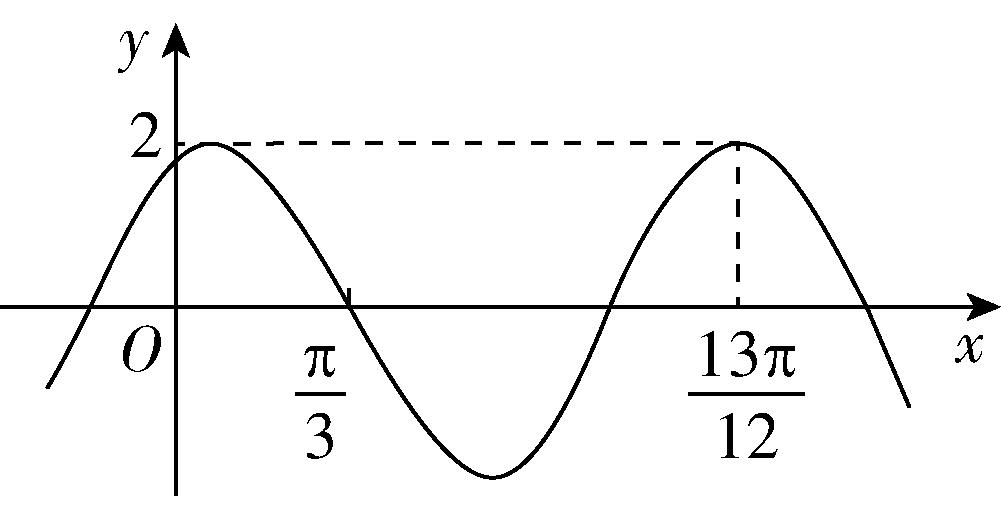
解析:设函数 $ f(x) $ 的最小正周期为 $ T $ ,由图象可知, $ \dfrac{3}{4}T=\dfrac{13\mathrm{\pi }}{12}-\dfrac{\mathrm{\pi }}{3}=\dfrac{3\mathrm{\pi }}{4} $ ,所以 $ T=\mathrm{\pi }=\dfrac{2\mathrm{\pi }}{\left|\omega \right|} $ ,所以 $ \omega =±2 $ .
当 $ \omega =2 $ 时,把点 $ (\dfrac{13\mathrm{\pi }}{12},2) $ 的坐标代入 $ f(x) $ 的解析式,得 $ 2 \cos \text{ }(\dfrac{13\mathrm{\pi }}{12}\omega +\varphi )=2 \cos (\dfrac{13\mathrm{\pi }}{12}×2+\varphi )=2 $ ,所以 $ \varphi =2k\mathrm{\pi }-\dfrac{\mathrm{\pi }}{6} $ , $ k\in \boldsymbol{Z} $ ,则 $ f(x)=2 \cos (2x+2k\mathrm{\pi }-\dfrac{\mathrm{\pi }}{6})=2 \cos (2x-\dfrac{\mathrm{\pi }}{6}) $ ;
当 $ \omega =-2 $ 时,将点 $ (\dfrac{13\mathrm{\pi }}{12},2) $ 的坐标代入 $ f(x) $ 的解析式,得 $ 2 \cos (\dfrac{13\mathrm{\pi }}{12}\omega +\varphi )=2 \cos [\dfrac{13\mathrm{\pi }}{12}×(-2)+\varphi ]=2 \cos (\dfrac{13\mathrm{\pi }}{12}×2-\varphi )=2 $ ,所以 $ \varphi =2k\mathrm{\pi }+\dfrac{\mathrm{\pi }}{6} $ , $ k\in \boldsymbol{Z} $ ,则 $ f(x)=2 \cos (2x-\varphi )=2 \cos \text{ }(2x-\dfrac{\mathrm{\pi }}{6}) $ .
综上得 $ f(x)=2 \cos \text{ }(2x-\dfrac{\mathrm{\pi }}{6}) $ ,所以 $ f(-\dfrac{7\mathrm{\pi }}{4})=2 \cos \text{ }[2×(-\dfrac{7\mathrm{\pi }}{4})-\dfrac{\mathrm{\pi }}{6}]=1 $ , $ f(\dfrac{4\mathrm{\pi }}{3})=2 \cos (2×\dfrac{4\mathrm{\pi }}{3}-\dfrac{\mathrm{\pi }}{6})=0 $ ,
所以 $ (f(x)-1)f(x) > 0 $ ,
所以 $ f(x) < 0 $ 或 $ f(x) > 1 $ ,
所以 $ \cos \text{ }(2x-\dfrac{\mathrm{\pi }}{6}) < 0 $ 或 $ \cos \text{ }(2x-\dfrac{\mathrm{\pi }}{6}) > \dfrac{1}{2} $ ,所以 $ \dfrac{\mathrm{\pi }}{2}+2k\mathrm{\pi } < 2x-\dfrac{\mathrm{\pi }}{6} < \dfrac{3\mathrm{\pi }}{2}+2k\mathrm{\pi } $ 或 $ -\dfrac{\mathrm{\pi }}{3}+2k\mathrm{\pi } < 2x-\dfrac{\mathrm{\pi }}{6} < \dfrac{\mathrm{\pi }}{3}+2k\mathrm{\pi } $ , $ k\in \boldsymbol{Z} $ ,
即 $ \dfrac{\mathrm{\pi }}{3}+k\mathrm{\pi } < x < \dfrac{5\mathrm{\pi }}{6}+k\mathrm{\pi } $ 或 $ -\dfrac{\mathrm{\pi }}{12}+k\mathrm{\pi } < x < \dfrac{\mathrm{\pi }}{4}+k\mathrm{\pi } $ , $ k\in \boldsymbol{Z} $ ,所以当 $ k=0 $ 时, $ x $ 能取到的最小正整数为2.
21.设函数 $ f(x)= \sin \omega x \cos \varphi + \cos \omega x \sin \varphi (\omega > 0,|\varphi | < \dfrac{\mathrm{\pi }}{2}) $ .
(1) 若 $ f(0)=-\dfrac{\sqrt{3}}{2} $ ,求 $ \varphi $ 的值.
(2) 已知 $ f(x) $ 在区间 $ [-\dfrac{\mathrm{\pi }}{3},\dfrac{2\mathrm{\pi }}{3}] $ 上单调递增, $ f(\dfrac{2\mathrm{\pi }}{3})=1 $ ,再从条件①、条件②、条件③这三个条件中选择一个作为已知,使函数 $ f(x) $ 存在,求 $ \omega $ , $ \varphi $ 的值.
条件①: $ f(\dfrac{\mathrm{\pi }}{3})=\sqrt{2} $ ;条件②: $ f(-\dfrac{\mathrm{\pi }}{3})=-1 $ ;
条件③: $ f(x) $ 在区间 $ [-\dfrac{\mathrm{\pi }}{2},-\dfrac{\mathrm{\pi }}{3}] $ 上单调递减.
注:如果选择的条件不符合要求,第(2)问得0分;如果选择多个符合要求的条件分别解答,按第一个解答计分.
答案:(1) 【解】 $ f(x)= \sin \omega x \cos \varphi + \cos \omega x \sin \varphi = \sin (\omega x+\varphi ) $ .
若 $ f(0)=-\dfrac{\sqrt{3}}{2} $ ,则 $ \sin \varphi =-\dfrac{\sqrt{3}}{2} $ .
因为 $ |\varphi | < \dfrac{\mathrm{\pi }}{2} $ ,所以 $ \varphi =-\dfrac{\mathrm{\pi }}{3} $ .
(2) 【解】选择条件①:因为 $ f(x)= \sin (\omega x+\varphi )\in [-1,1] $ , $ f(\dfrac{\mathrm{\pi }}{3})=\sqrt{2}\notin [-1,1] $ ,矛盾,所以条件①不符合题意,故不选条件①.
选择条件②:因为 $ f(x)= \sin (\omega x+\varphi ) $ 在 $ [-\dfrac{\mathrm{\pi }}{3},\dfrac{2\mathrm{\pi }}{3}] $ 上单调递增, $ f(-\dfrac{\mathrm{\pi }}{3})=-1 $ , $ f(\dfrac{2\mathrm{\pi }}{3})=1 $ ,所以 $ \dfrac{2\mathrm{\pi }}{3}-(-\dfrac{\mathrm{\pi }}{3})=\dfrac{T}{2}=\dfrac{\mathrm{\pi }}{\omega } $ ,所以 $ \omega =1 $ ,所以 $ f(x)= \sin (x+\varphi ) $ .又因为 $ f(\dfrac{2\mathrm{\pi }}{3})= \sin (\dfrac{2\mathrm{\pi }}{3}+\varphi )=1 $ ,所以 $ \dfrac{2\mathrm{\pi }}{3}+\varphi =2k\mathrm{\pi }+\dfrac{\mathrm{\pi }}{2} $ , $ k\in \boldsymbol{Z} $ ,解得 $ \varphi =-\dfrac{\mathrm{\pi }}{6}+2k\mathrm{\pi } $ , $ k\in \boldsymbol{Z} $ .因为 $ |\varphi | < \dfrac{\mathrm{\pi }}{2} $ ,所以 $ \varphi =-\dfrac{\mathrm{\pi }}{6} $ .
选择条件③:由题意, $ f(x) $ 在 $ [-\dfrac{4\mathrm{\pi }}{3},-\dfrac{\mathrm{\pi }}{3}] $ 上单调递减,在 $ [-\dfrac{\mathrm{\pi }}{3},\dfrac{2\mathrm{\pi }}{3}] $ 上单调递增,所以 $ -\dfrac{\mathrm{\pi }}{3} $ 为 $ f(x) $ 的最小值点,且 $ \dfrac{2\mathrm{\pi }}{3}-(-\dfrac{\mathrm{\pi }}{3})=\dfrac{T}{2}=\dfrac{\mathrm{\pi }}{\omega } $ ,所以 $ \omega =1 $ ,所以 $ f(x)= \sin (x+\varphi ) $ .
又因为 $ f(\dfrac{2\mathrm{\pi }}{3})= \sin (\dfrac{2\mathrm{\pi }}{3}+\varphi )=1 $ ,所以 $ \dfrac{2\mathrm{\pi }}{3}+\varphi =2k\mathrm{\pi }+\dfrac{\mathrm{\pi }}{2} $ , $ k\in \boldsymbol{Z} $ ,解得 $ \varphi =-\dfrac{\mathrm{\pi }}{6}+2k\mathrm{\pi } $ , $ k\in \boldsymbol{Z} $ .因为 $ |\varphi | < \dfrac{\mathrm{\pi }}{2} $ ,所以 $ \varphi =-\dfrac{\mathrm{\pi }}{6} $ .
解析:
二、刷原创
1.已知函数 $ f(x) $ 的定义域为 $ \boldsymbol{R} $ ,且 $ \forall {x}_{1} $ , $ {x}_{2}\in \boldsymbol{R} $ 都有 $ |f({x}_{1})+f({x}_{2})|\leqslant | \sin \omega {x}_{1}+ \sin \omega {x}_{2}| $ ,常数 $ \omega \in \boldsymbol{R} $ ,则( )
A. $ f(x) $ 的周期为 $ \dfrac{2\mathrm{\pi }}{|\omega |} $
B. $ f(x) $ 为增函数
C. $ f(x) $ 为既奇又偶函数
D. $ f(x) $ 为减函数
答案:C
解析:由题意,当 $ \omega =0 $ 时, $ \forall {x}_{1} $ , $ {x}_{2}\in \boldsymbol{R} $ 都有 $ |f({x}_{1})+f({x}_{2})|\leqslant 0 $ ,则 $ |f(x)_{ \max }|+|f(x)_{ \max }|\leqslant 0 $ ,且 $ |f(x)_{ \min }|+|f(x)_{ \min }|\leqslant 0 $ ,故 $ |f(x)_{ \min }|=|f(x)_{ \max }|=0 $ ,即 $ f(x)=0 $ .
易知 $ f(x)=0 $ 没有最小正周期,不为增函数也不为减函数,且是既奇又偶函数,故选 $ \mathrm{C} $ .
2.若 $ \forall x\in [\dfrac{\mathrm{\pi }}{4},\dfrac{\mathrm{\pi }}{2}) $ ,都有 $ ax+ \sin x( \sin x+ \cos x)\geqslant 0 $ ,则实数 $ a $ 的取值范围是 .
答案: $ {a|a\geqslant -\dfrac{2}{\mathrm{\pi }}} $
解析:记函数 $ f(x)= \sin x( \sin x+ \cos x)=\dfrac{1- \cos 2x}{2}+\dfrac{ \sin 2x}{2}=\dfrac{1}{2}[1+\sqrt{2} \sin (2x-\dfrac{\mathrm{\pi }}{4})] $ ,
由 $ x\in [\dfrac{\mathrm{\pi }}{4},\dfrac{\mathrm{\pi }}{2}) $ ,得 $ 2x-\dfrac{\mathrm{\pi }}{4}\in [\dfrac{\mathrm{\pi }}{4} $ , $ \dfrac{3\mathrm{\pi }}{4}) $ ,故函数 $ f(x) $ 在区间 $ [\dfrac{\mathrm{\pi }}{4} $ , $ \dfrac{3\mathrm{\pi }}{8}) $ 上单调递增,在区间 $ (\dfrac{3\mathrm{\pi }}{8} $ , $ \dfrac{\mathrm{\pi }}{2}) $ 上单调递减.又 $ ax+ \sin x( \sin x+ \cos x)\geqslant 0 $ 等价于 $ -ax\leqslant f(x) $ ,如图,作出函数 $ y=-ax $ 与函数 $ y=f(x) $ 在区间 $ [\dfrac{\mathrm{\pi }}{4} $ , $ \dfrac{\mathrm{\pi }}{2}) $ 上的图象,由图可知,函数
$ y=-ax $ 在 $ [\dfrac{\mathrm{\pi }}{4},\dfrac{\mathrm{\pi }}{2}) $ 上的图象不在过点 $ (0,0) $ , $ (\dfrac{\mathrm{\pi }}{2} $ , $ 1) $ 的直线 $ y=\dfrac{2}{\mathrm{\pi }}x $ 的上方时,满足题意,故 $ -a\leqslant \dfrac{2}{\mathrm{\pi }} $ ,即实数 $ a $ 的取值范围为 $ {a|a\geqslant -\dfrac{2}{\mathrm{\pi }}} $ .

3.已知点 $ O $ 在半径为 $ r $ 的圆 $ E $ 上,直线 $ AD\perp OE $ ,且圆心 $ E $ 到 $ AD $ 的距离为 $ m(1 < \dfrac{m}{r} < \dfrac{3}{2}) $ ,如图.以 $ O $ 为顶点,射线 $ OE $ 为始边,角 $ \alpha $ , $ \beta (-\dfrac{\mathrm{\pi }}{2} < \alpha \leqslant 0,0\leqslant \beta < \dfrac{\mathrm{\pi }}{2}) $ 的终边与圆 $ E $ 分别交于点 $ B $ , $ C $ ,点 $ B $ , $ C $ 到直线 $ AD $ 的距离与到点 $ O $ 的距离相等.
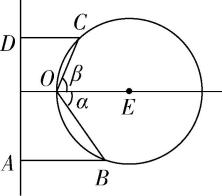
(1) 求 $ \cos \alpha + \cos \beta $ 的值;
(2) 求 $ \sin \alpha - \sin \beta $ 的取值范围.
答案:(1) 【解】以点 $ O $ 为坐标原点,以 $ OE $ 所在直线为 $ x $ 轴建立平面直角坐标系,如图所示,则 $ B(2r{ \cos }^{2}\alpha ,2r \cos \alpha \sin \alpha ) $ , $ C(2r{ \cos }^{2}\beta ,2r \cos \beta \sin \beta ) $ .
又 $ |OB|=|AB| $ , $ |OC|=|CD| $ ,则 $ \begin{cases}2r \cos \alpha =2r{ \cos }^{2}\alpha +m-r,\\ 2r \cos \beta =2r{ \cos }^{2}\beta +m-r,\end{cases} $
两式相减,得 $ \cos \alpha + \cos \beta =1 $ .

(2) 【解】因为 $ ( \cos \alpha + \cos \beta )^{2}+{\left( \sin \alpha - \sin \beta \right) ^ {2}}=2+2 ( \cos \alpha \cos \beta - \sin \alpha \sin \beta )=2+2 \cos (\alpha +\beta ) $ ,又 $ -\dfrac{\mathrm{\pi }}{2} < \alpha \leqslant 0 $ , $ 0\leqslant \beta < \dfrac{\mathrm{\pi }}{2} $ ,所以 $ 0 < \cos (\alpha +\beta )\leqslant 1 $ ,
故 $ 2 < ( \cos \alpha + \cos \beta )^{2}+{\left( \sin \alpha - \sin \beta \right) ^ {2}}\leqslant 4 $ ,所以 $ 1 < ( \sin \alpha - \sin \beta )^{2}\leqslant 3 $ ,所以 $ \sin \alpha - \sin \beta \in [-\sqrt{3},-1)\cup (1,\sqrt{3}] $ .
又由 $ -\dfrac{\mathrm{\pi }}{2} < \alpha \leqslant 0 $ , $ 0\leqslant \beta < \dfrac{\mathrm{\pi }}{2} $ ,可知 $ -1 < \sin \alpha \leqslant 0 $ , $ 0\leqslant \sin \beta < 1 $ ,故 $ -2 < \sin \alpha - \sin \beta \leqslant 0 $ ,故 $ \sin \alpha - \sin \beta $ 的取值范围为 $ [-\sqrt{3},-1) $ .
解析:
4.已知 $ \omega > 0 $ , $ 0 < \varphi < \mathrm{\pi } $ ,对任意 $ x\in \boldsymbol{R} $ 都有 $ \cos [2(x-\varphi )]\leqslant \sin \omega x $ ,求函数 $ f(x)= \cos (\omega x+\varphi ) $ 的单调递增区间.
答案:【解】因为对任意 $ x\in \boldsymbol{R} $ 都有 $ \cos [2(x-\varphi )]\leqslant \sin \omega x $ ,
可令 $ x=-\dfrac{\mathrm{\pi }}{2\omega } $ ,得 $ \cos (\dfrac{\mathrm{\pi }}{\omega }+2\varphi )\leqslant -1 $ ,又由余弦函数的有界性知 $ \cos (\dfrac{\mathrm{\pi }}{\omega }+2\varphi )=-1 $ ,
故 $ \dfrac{\mathrm{\pi }}{\omega }+2\varphi =(2k+1)\mathrm{\pi } $ , $ k\in \boldsymbol{Z}.① $
又令 $ x=\varphi $ ,则 $ 1\leqslant \sin \omega \varphi $ ,故由正弦函数的有界性知 $ \sin \omega \varphi =1 $ ,故 $ \omega \varphi =\dfrac{\mathrm{\pi }}{2}+2m\mathrm{\pi } $ , $ m\in \boldsymbol{Z} $ ,②
联立方程 $ ①② $ ,解得 $ \omega =\dfrac{2(2m+1)}{2k+1} $ 对任意 $ m\in \boldsymbol{Z} $ , $ k\in \boldsymbol{Z} $ 恒成立,因此, $ m=k $ , $ \omega =2 $ ,所以 $ \varphi =\dfrac{\mathrm{\pi }}{4}+k\mathrm{\pi } $ , $ k\in \boldsymbol{Z} $ ,又 $ 0 < \varphi < \mathrm{\pi } $ ,所以 $ \varphi =\dfrac{\mathrm{\pi }}{4} $ .
故 $ f(x)= \cos (2x+\dfrac{\mathrm{\pi }}{4}) $ ,令 $ (2k-1)\mathrm{\pi }\leqslant 2x+\dfrac{\mathrm{\pi }}{4}\leqslant 2k\mathrm{\pi } $ , $ k\in \boldsymbol{Z} $ ,
得 $ (k-\dfrac{5}{8})\mathrm{\pi }\leqslant x\leqslant (k-\dfrac{1}{8})\mathrm{\pi } $ , $ k\in \boldsymbol{Z} $ ,即 $ f(x) $ 的单调递增区间为 $ [ (k-\dfrac{5}{8} )\mathrm{\pi } $ , $ (k-\dfrac{1}{8} )\mathrm{\pi } ] $ , $ k\in \boldsymbol{Z} $ .
解析:
5.已知函数 $ f(x)=a{x}^{2}+bx+c(a\ne 0) $ ,对任意 $ x\in \boldsymbol{R} $ 都有 $ f( \cos x)\geqslant 0 $ , $ f(2+ \sin x)\leqslant 0 $ .
(1) 求 $ \dfrac{c}{a} $ 的取值范围;
(2) 若 $ f( \sin x) $ 的最大值为10,求正实数 $ a $ 的取值范围.
答案:(1) 【解】因为 $ -1\leqslant \sin x\leqslant 1 $ ,所以 $ 1\leqslant 2+ \sin x\leqslant 3 $ ,又 $ -1\leqslant \cos x\leqslant 1 $ ,则 $ f(1)\geqslant 0 $ , $ f(1)\leqslant 0 $ ,故 $ f(1)=0 $ ,即函数 $ f(x) $ 有一个零点为1.
设 $ f(x)=a(x-1)(x-\dfrac{c}{a}) $ ,则当 $ a > 0 $ 时, $ f(x)\leqslant 0 $ 的解集 $ M={x|1\leqslant x\leqslant \dfrac{c}{a}}(\dfrac{c}{a}\geqslant 1) $ 或 $ {x|\dfrac{c}{a}\leqslant x\leqslant 1}(\dfrac{c}{a} < 1) $ .
又 $ f(2+ \sin x)\leqslant 0 $ 对任意 $ x\in \boldsymbol{R} $ 恒成立,故 $ [1,3]\subseteq M $ ,从而 $ \dfrac{c}{a}\geqslant 3 $ .
经验证,当 $ \dfrac{c}{a}\geqslant 3 $ 时,满足对任意 $ x\in \boldsymbol{R} $ , $ f( \cos x)\geqslant 0 $ .
当 $ a < 0 $ 时, $ f(x)\geqslant 0 $ 的解集 $ M={x|1\leqslant x\leqslant \dfrac{c}{a}}(\dfrac{c}{a}\geqslant 1) $ 或 $ {x|\dfrac{c}{a}\leqslant x\leqslant 1}(\dfrac{c}{a} < 1) $ ,
又 $ f( \cos x)\geqslant 0 $ 对任意 $ x\in \boldsymbol{R} $ 恒成立,故 $ [-1,1]\subseteq M $ ,因此 $ \dfrac{c}{a}\leqslant -1 $ .
经验证,当 $ \dfrac{c}{a}\leqslant -1 $ 时,满足对任意 $ x\in \boldsymbol{R} $ , $ f(2+ \sin x)\leqslant 0 $ .
综上所述, $ \dfrac{c}{a} $ 的取值范围为 $ (-\mathrm{\infty },-1]\cup [3,+\mathrm{\infty }) $ .
(2) 【解】由(1)知 $ f(x)=a[x-\dfrac{1}{2}(1+\dfrac{c}{a})]^{2}+c-\dfrac{{\left(a+c\right) ^ {2}}}{4a} $ ,
又 $ a > 0 $ ,则由(1)知 $ \dfrac{c}{a}\geqslant 3 $ ,故 $ f(x) $ 图象的对称轴为直线 $ x=\dfrac{1}{2}(1+\dfrac{c}{a})\geqslant 2 $ .因为 $ \sin x\in [-1,1] $ ,
故 $ f ( \sin x)_{ \max }=f (-1 )=10 $ ,即 $ 2a(1+\dfrac{c}{a})=10 $ ,即 $ a+c=5 $ ,所以 $ \dfrac{c}{a}=\dfrac{5-a}{a}\geqslant 3 $ ,解得 $ 0 < a\leqslant \dfrac{5}{4} $ ,即正实数 $ a $ 的取值范围为 $ (0,\dfrac{5}{4}] $ .
解析:











