专练2 开放题专练

3．（条件开放）已知集合 $ A=｛x|-2 < x\leqslant 1｝ $ ， $ B=｛x|{x}^{2}-2mx+{m}^{2}-4 < 0｝ $ ， $ C=｛x\left| \right|x+m| < 2+3m｝ $ ， $ D=｛x|\dfrac{4-m}{x-2}\leqslant -2｝ $ .

（1）当 $ m=1 $ 时，求集合 $ D $ .

（2）从集合 $ B $ ， $ C $ ， $ D $ 中任选一个，补充在下面的问题中，并解答问题.

已知 $ p:x\in A $ , $ q:x\in $ ，若存在实数 $ m $ ，满足 $ q $ 是 $ p $ 的必要不充分条件，求出 $ m $ 的取值范围；若不存在，请说明理由.

注：如果选择多个条件分别解答，按第一个解答计分.

答案：

见解析

解析：

（1）当 $ m=1 $ 时，不等式 $ \dfrac{3}{x-2}\leqslant -2 $ ，即 $ \dfrac{2x-1}{x-2}\leqslant 0 $ ，所以 $ \begin{cases}\left(2x-1\right)\left(x-2\right)\leqslant 0,\\ x-2\ne 0,\end{cases} $

解得 $ \dfrac{1}{2}\leqslant x < 2 $ ，所以 $ D=｛x|\dfrac{1}{2}\leqslant x < 2｝ $ .

（2）选 $ B=｛x|(x-m+2)(x-m-2) < 0｝=｛x|m-2 < x < m+2｝ $ .

因为 $ q $ 是 $ p $ 的必要不充分条件，所以 $ A $ 是 $ B $ 的真子集，则 $ \begin{cases}m-2\leqslant -2,\\ m+2 > 1,\end{cases} $ 解得 $ -1 < m\leqslant 0 $ ，即实数 $ m $ 的取值范围是 $ (-1,0] $ .

选 $ C=｛x\left| \right|x+m| < 2+3m｝ $ .

因为 $ q $ 是 $ p $ 的必要不充分条件，所以 $ A $ 是 $ C $ 的真子集，则集合 $ C\ne \mathrm{⌀} $ ，则不等式 $ \left|x+m\right| < 2+3m $ 有解，所以 $ 2+3m > 0 $ ，即 $ m > -\dfrac{2}{3} $ ，则 $ C=｛x\left| \right|x+m\left| < 2+3m｝=｛x\right|-4m-2 < x < 2m+2｝ $ ，所以 $ \begin{cases}m > -\dfrac{2}{3},\\ -4m-2\leqslant -2,\\ 2m+2 > 1,\end{cases} $ 解得 $ m\geqslant 0 $ ，即实数 $ m $ 的取值范围是 $ [0,+\mathrm{\infty }) $ .

选 $ D=｛x|\dfrac{4-m}{x-2}\leqslant -2｝ $ .

因为 $ q $ 是 $ p $ 的必要不充分条件，所以 $ A $ 是 $ D $ 的真子集.

解不等式 $ \dfrac{4-m}{x-2}\leqslant -2 $ ，即解不等式 $ \dfrac{2x-m}{x-2}\leqslant 0 $ ，所以 $ \begin{cases}\left(2x-m\right)\left(x-2\right)\leqslant 0,\\ x-2\ne 0.\end{cases} $ 当 $ m=4 $ 时，不等式无解，此时 $ D=\mathrm{⌀} $ ，与题意矛盾；

当 $ m > 4 $ 时，不等式的解集为 $ ｛x|2 < x\leqslant \dfrac{m}{2}｝ $ ，此时 $ A $ 不是 $ D $ 的真子集，故舍去；

当 $ m < 4 $ 时，不等式的解集为 $ ｛x|\dfrac{m}{2}\leqslant x < 2｝ $ ，即 $ D=｛x|\dfrac{m}{2}\leqslant x < 2｝ $ ，

则 $ \begin{cases}\dfrac{m}{2}\leqslant -2,\\ 2 > 1,\end{cases} $ 解得 $ m\leqslant -4 $ .

综上，实数 $ m $ 的取值范围是 $ (-\mathrm{\infty },-4] $ .

4．（条件开放）已知指数函数 $ f (x )={a}^{x} (a > 0 $ ，且 $ a\ne 1) $ 的图象过点 $ (m,n) $ ，在 $ \mathrm{①}\sqrt{2m-2}+\sqrt{9-3n}=0 $ ；②函数 $ y={x}^{2}-2x+4 $ 图象的顶点坐标为 $ (m,n) $ ；③函数 $ y={ \log }_{b}x+3(b > 0 $ ，且 $ b\ne 1) $ 的图象过定点 $ (m,n) $ ，这三个条件中任选一个，回答下列问题.

（1）求 $ f(x) $ 的解析式，判断并证明 $ g(x)=f(x)+\dfrac{1}{f(x)} $ 的奇偶性；

（2）解不等式 $ { \log }_{a}(1+x) < { \log }_{a}(2-x) $ .

注：如果选择多个条件分别解答，按第一个解答计分.

答案：

（1）【解】若选①：因为 $ \sqrt{2m-2}+\sqrt{9-3n}=0 $ ，所以 $ 2m-2=9-3n=0 $ ，解得 $ m=1 $ , $ n=3 $ ，

可知指数函数 $ f(x)={a}^{x} $ 的图象过点 $ (1,3) $ ，所以 $ a=3 $ ，所以 $ f(x)={3}^{x} $ .

则 $ g(x)={3}^{x}+{3}^{-x} $ 的定义域为 $ \boldsymbol{R} $

，且 $ g(-x)={3}^{-x}+{3}^{x}=g(x) $ ，

所以 $ g(x) $ 为偶函数.

若选②：函数 $ y={x}^{2}-2x+4={\left(x-1\right) ^ {2}}+3 $ 的图象的顶点坐标为 $ (1,3) $ ，

可知指数函数 $ f(x)={a}^{x} $ 的图象过点 $ (1,3) $ ，即 $ a=3 $ ，所以 $ f(x)={3}^{x} $ .

则 $ g(x)={3}^{x}+{3}^{-x} $ 的定义域为 $ \boldsymbol{R} $ ，且 $ g(-x)={3}^{-x}+{3}^{x}=g(x) $ ，

所以 $ g(x) $ 为偶函数.

若选③：由 $ y={ \log }_{b}x $ 的图象过定点 $ (1,0) $ ，可知函数 $ y={ \log }_{b}x+3 $ 的图象过定点 $ (1,3) $ ，

则指数函数 $ f(x)={a}^{x} $ 的图象过点 $ (1,3) $ ，即 $ a=3 $ ，所以 $ f(x)={3}^{x} $ .

则 $ g(x)={3}^{x}+{3}^{-x} $ 的定义域为 $ \boldsymbol{R} $ ，且 $ g(-x)={3}^{-x}+{3}^{x}=g(x) $ ，

所以 $ g(x) $ 为偶函数.

（2）【解】由（1）可知 $ a=3 $ ，则 $ { \log }_{3}(1+x) < { \log }_{3}(2-x) $ ，又 $ y={ \log }_{3}x $ 在定义域 $ (0,+\mathrm{\infty }) $ 上单调递增，

所以 $ \begin{cases}1+x > 0,\\ 2-x > 0,\\ 1+x < 2-x,\end{cases} $ 解得 $ -1 < x < \dfrac{1}{2} $ ，

所以所求不等式的解集为 $ (-1,\dfrac{1}{2}) $ .

解析：

5．（条件开放）现有三个条件：

①对任意的 $ x\in \boldsymbol{R} $ 都有 $ f(x+1)-f(x)=2x-2 $ ；

②不等式 $ f(x) < 0 $ 的解集为 $ ｛x|1 < x < 2｝ $ ；

③函数 $ y=f(x) $ 的图象过点 $ (3,2) $ .

请你在上述三个条件中任选两个补充到下面的问题中，并求解：

已知二次函数 $ f(x)=a{x}^{2}+bx+c(a\ne 0) $ ，且满足 .（填所选条件的序号）

（1）求函数 $ f(x) $ 的解析式；

（2）设 $ g(x)=\dfrac{f(x)+x-2}{x} $ ，若不等式 $ g({3}^{x})-k\cdot {3}^{x}\geqslant 0 $ 在 $ x\in [-1,0) $ 上恒成立，求实数 $ k $ 的取值范围.

注：如果选择多组条件分别解答，按第一个解答计分.

答案：

见解析

解析：

（1）条件①：因为 $ f(x)=a{x}^{2}+bx+c(a\ne 0) $ ，所以 $ f(x+1)-f(x)=a{\left(x+1\right) ^ {2}}+b(x+1)+c-(a{x}^{2}+bx+c)=2ax+a+b=2x-2 $ ，即 $ 2(a-1)x+a+b+2=0 $ 对任意的 $ x\in \boldsymbol{R} $ 恒成立，所以 $ \begin{cases}a-1=0,\\ a+b+2=0,\end{cases} $ 解得 $ \begin{cases}a=1,\\ b=-3.\end{cases} $

条件②：因为不等式 $ f(x) < 0 $ 的解集为 $ ｛x|1 < x < 2｝ $ ，

所以方程 $ a{x}^{2}+bx+c=0 $ 的两根为1和2，

所以 $ \begin{cases}1+2=-\dfrac{b}{a},\\ 1×2=\dfrac{c}{a},\end{cases} $ 解得 $ \begin{cases}b=-3a,\\ c=2a,\end{cases} $ 且 $ a > 0 $ .

条件③：因为函数 $ y=f(x) $ 的图象过点 $ (3,2) $ ，所以 $ 9a+3b+c=2 $ .

若选择条件①②，则 $ a=1 $ ， $ b=-3 $ ， $ c=2 $ ，此时 $ f(x)={x}^{2}-3x+2 $ .

若选择条件 $ \mathrm{①}\mathrm{③} $ ,则 $ a=1 $ ， $ b=-3 $ ， $ c=2 $ ，此时 $ f(x)={x}^{2}-3x+2 $ .

若选择条件 $ \mathrm{②}\mathrm{③} $ ,则 $ a=1 $ ， $ b=-3 $ ， $ c=2 $ ，此时 $ f(x)={x}^{2}-3x+2 $ .

（2）由（1）知 $ f(x)={x}^{2}-3x+2 $ ，所以 $ g(x)=x-2 $ .

所以 $ g({3}^{x})-k\cdot {3}^{x}={3}^{x}-2-k\cdot {3}^{x}\geqslant 0 $ ，所以 $ k\leqslant 1-\dfrac{2}{{3}^{x}} $ 在 $ x\in [-1,0) $ 上恒成立.

设 $ h(x)=1-\dfrac{2}{{3}^{x}} $ ， $ x\in [-1,0) $ ，则 $ h(x) $ 在 $ [-1,0) $ 上单调递增，所以 $ h{(x)}_{ \min }=h(-1)=-5 $ ，所以 $ k\leqslant -5 $ .

故实数 $ k $ 的取值范围是 $ (-\mathrm{\infty },-5] $ .

6．（条件开放）已知角 $ \alpha $ 是第一象限角，且 .在 $ \mathrm{①} \sin \alpha =\dfrac{\sqrt{6}}{3} $ ， $ \mathrm{②}{ \tan }^{2}\alpha +\sqrt{2} \tan \alpha -4=0 $ 这两个条件中任选一个，补充到上面的横线中，并解答下面的问题.

（1）求 $ \tan \alpha $ 的值；

（2）求 $ \cos (\alpha +\mathrm{\pi }) \cos (\alpha -3\mathrm{\pi })-2\sqrt{2} \cos (\alpha +\dfrac{3\mathrm{\pi }}{2})\cdot \sin (\alpha -\dfrac{\mathrm{\pi }}{2}) $ 的值.

注：如果选择两个条件分别解答，按第一个解答计分.

答案：

（1）【解】选择条件①： $ \because $ 角 $ \alpha $ 是第一象限角， $ \sin \alpha =\dfrac{\sqrt{6}}{3} $ ，

$ \therefore \cos \alpha =\sqrt{1-{ \sin }^{2}\alpha }=\sqrt{1-{\left(\dfrac{\sqrt{6}}{3}\right) ^ {2}}}=\dfrac{\sqrt{3}}{3} $ ，故 $ \tan \alpha =\dfrac{ \sin \alpha }{ \cos \alpha }=\sqrt{2} $ .

选择条件②： $ \because { \tan }^{2}\alpha +\sqrt{2} \tan \alpha -4=( \tan \alpha +2\sqrt{2})( \tan \alpha -\sqrt{2})=0 $ ，

$ \therefore \tan \alpha =\sqrt{2} $ 或 $ \tan \alpha =-2\sqrt{2} $ ，

又角 $ \alpha $ 是第一象限角， $ \therefore \tan \alpha =\sqrt{2} $ .

（2）【解】选择条件①：

由（1）可知， $ \cos \alpha =\dfrac{\sqrt{3}}{3} $ , $ \cos (\alpha +\mathrm{\pi }) \cos (\alpha -3\mathrm{\pi })-2\sqrt{2} \cos (\alpha +\dfrac{3\mathrm{\pi }}{2}) \sin (\alpha -\dfrac{\mathrm{\pi }}{2}) $

$ =(- \cos \alpha )\cdot (- \cos \alpha )-2\sqrt{2} \sin \alpha \cdot (- \cos \alpha ) $

$ ={\left(-\dfrac{\sqrt{3}}{3}\right) ^ {2}}-2\sqrt{2}×\dfrac{\sqrt{6}}{3}×(-\dfrac{\sqrt{3}}{3})=\dfrac{5}{3} $ .

选择条件②：

由（1）可知， $ \tan \alpha =\sqrt{2} $ , $ \cos (\alpha +\mathrm{\pi }) \cos (\alpha -3\mathrm{\pi })-2\sqrt{2} \cos (\alpha +\dfrac{3\mathrm{\pi }}{2}) \sin (\alpha -\dfrac{\mathrm{\pi }}{2}) $

$ =(- \cos \alpha )\cdot (- \cos \alpha )-2\sqrt{2} \sin \alpha \cdot (- \cos \alpha ) $

$ ={ \cos }^{2}\alpha +2\sqrt{2} \sin \alpha \cdot \cos \alpha $

$ =\dfrac{{ \cos }^{2}\alpha +2\sqrt{2} \sin \alpha \cdot \cos \alpha }{{ \sin }^{2}\alpha +{ \cos }^{2}\alpha } $

$ =\dfrac{1+2\sqrt{2} \tan \alpha }{{ \tan }^{2}\alpha +1}=\dfrac{1+2\sqrt{2}×\sqrt{2}}{{\left(\sqrt{2}\right) ^ {2}}+1}=\dfrac{5}{3} $ .

解析：

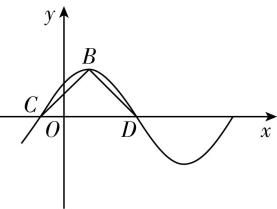
7．（条件开放）如图是函数 $ f(x)=A \sin (\omega x+\varphi ) $ 的部分图象,其中 $ \omega > 0 $ , $ 0 < \varphi < \mathrm{\pi } $ , $ B $ 为图象的最高点, $ C $ , $ D $ 为图象与 $ x $ 轴的交点,且 $ △BCD $ 为等腰直角三角形, $ CD=2 $ , .

在 $ \mathrm{①}f(x+\dfrac{1}{2})=f(-x+\dfrac{1}{2}) $ ； $ \mathrm{②}f(x-\dfrac{1}{2}) $ 是奇函数； $ \mathrm{③}f(0)=\dfrac{\sqrt{2}}{2} $ 这三个条件中任选一个,补充在横线处并解答.

试题资源网 https://stzy.com

（1）求函数 $ f(x) $ 的解析式；

（2）设 $ g(x)=f(\dfrac{2}{\mathrm{\pi }}x+\dfrac{1}{2}) $ ,不等式 $ m{ \sin }^{2}x-g(x)\leqslant 4-6m $ 对于 $ \forall x\in \boldsymbol{R} $ 恒成立,求 $ m $ 的取值范围.

注：如果选择多个条件分别解答，按第一个解答计分.

答案：

（1）【解】 $ \because △BCD $ 为等腰直角三角形, $ CD=2 $ , $ \therefore A=1 $ ,且 $ f(x) $ 的最小正周期 $ T $ 满足 $ \dfrac{T}{2}=2 $ ,即 $ T=4 $ ，

$ \therefore T=\dfrac{2\mathrm{\pi }}{|\omega |}=4 $ ,又 $ \omega > 0 $ , $ \therefore \omega =\dfrac{\mathrm{\pi }}{2} $ ,

则 $ f(x)= \sin (\dfrac{\mathrm{\pi }}{2}x+\varphi ) $ .

若选①,由 $ f(x+\dfrac{1}{2})=f(-x+\dfrac{1}{2}) $ ,得函数 $ f(x) $ 的图象关于直线 $ x=\dfrac{1}{2} $ 对称,

则 $ \dfrac{\mathrm{\pi }}{2}×\dfrac{1}{2}+\varphi =\dfrac{\mathrm{\pi }}{2}+k\mathrm{\pi }(k\in \boldsymbol{Z}) $ , $ \therefore \varphi =\dfrac{\mathrm{\pi }}{4}+k\mathrm{\pi }(k\in \boldsymbol{Z}) $ , $ \because 0 < \varphi < \mathrm{\pi } $ , $ \therefore \varphi =\dfrac{\mathrm{\pi }}{4} $ .

故函数 $ f(x) $ 的解析式为 $ f(x)= \sin (\dfrac{\mathrm{\pi }}{2}x+\dfrac{\mathrm{\pi }}{4}) $ .

若选②, $ \because f(x-\dfrac{1}{2})= \sin (\dfrac{\mathrm{\pi }}{2}x-\dfrac{\mathrm{\pi }}{4}+\varphi ) $ 是奇函数,

$ \therefore -\dfrac{\mathrm{\pi }}{4}+\varphi =k\mathrm{\pi }(k\in \boldsymbol{Z}) $ , $ \therefore \varphi =\dfrac{\mathrm{\pi }}{4}+k\mathrm{\pi }(k\in \boldsymbol{Z}) $ , $ \because 0 < \varphi < \mathrm{\pi } $ , $ \therefore \varphi =\dfrac{\mathrm{\pi }}{4} $ .

故函数 $ f(x) $ 的解析式为 $ f(x)= \sin (\dfrac{\mathrm{\pi }}{2}x+\dfrac{\mathrm{\pi }}{4}) $ .

若选③, $ f(0)= \sin \varphi =\dfrac{\sqrt{2}}{2} $ ,结合图象和 $ 0 < \varphi < \mathrm{\pi } $ ,可得 $ \varphi =\dfrac{\mathrm{\pi }}{4} $ .

故函数 $ f(x) $ 的解析式为 $ f(x)= \sin (\dfrac{\mathrm{\pi }}{2}x+\dfrac{\mathrm{\pi }}{4}) $ .

（2）【解】由（1）得 $ g(x)=f(\dfrac{2}{\mathrm{\pi }}x+\dfrac{1}{2})= \sin (x+\dfrac{\mathrm{\pi }}{2})= \cos x $ ,

$ \therefore m{ \sin }^{2}x-g(x)\leqslant 4-6m $ ,即 $ m{ \sin }^{2}x- \cos x-4+6m\leqslant 0 $ ,

$ \therefore m{ \cos }^{2}x+ \cos x-7m+4\geqslant 0 $ 对于 $ \forall x\in \boldsymbol{R} $ 恒成立.

令 $ t= \cos x $ , $ t\in [-1,1] $ ,则 $ m{t}^{2}+t-7m+4\geqslant 0 $ 对 $ \forall t\in [-1,1] $ 恒成立,

$ \therefore m\leqslant -\dfrac{t+4}{{t}^{2}-7} $ 在 $ t\in [-1,1] $ 时恒成立.

又 $ \dfrac{{t}^{2}-7}{t+4}=\dfrac{{\left(t+4\right) ^ {2}}-8(t+4)+9}{t+4}=(t+4)+\dfrac{9}{t+4}-8 $ ,

令 $ n=t+4 $ , $ n\in [3,5] $ ,则 $ y=n+\dfrac{9}{n}-8 $ 在 $ [3,5] $ 上单调递增,

$ \therefore y\in [-2,-\dfrac{6}{5}] $ ,即 $ \dfrac{{t}^{2}-7}{t+4}\in [-2,-\dfrac{6}{5}] $ , $ \therefore -\dfrac{t+4}{{t}^{2}-7}\in [\dfrac{1}{2},\dfrac{5}{6}] $ , $ \therefore m\leqslant \dfrac{1}{2} $ ,

故 $ m $ 的取值范围为 $ (-\mathrm{\infty },\dfrac{1}{2}] $ .

解析：

8．（条件开放）小颖同学在学习探究活动中，定义了一种运算“ $ \otimes $ ”：对于任意实数 $ a $ ， $ b $ ，都有 $ a\otimes b= \lg ({10}^{a}+{10}^{b}) $ .通过研究发现新运算满足交换律： $ a\otimes b=b\otimes a $ .小颖提出了两个猜想： $ \forall x $ ， $ y $ ， $ z\in \boldsymbol{R} $ ， $ \mathrm{①}(x\otimes y)\otimes z=x\otimes (y\otimes z) $ ； $ \mathrm{②}(x\otimes y)+z=(x+z)\otimes (y+z) $ .

（1）请你任选其中一个猜想，判断其正确与否，若正确，进行证明；若错误，请说明理由.

（2）设 $ a > 0 $ 且 $ a\ne 1 $ ， $ s={ \log }_{a}[(x-2a)(x-4a)] $ ，当 $ 0 < m < n < 2a $ 时，若函数 $ f(x)=(s+1)\otimes (s+3)-1- \lg 101 $ 在区间 $ [m,n] $ 上的值域为 $ [{ \log }_{a}n,{ \log }_{a}m] $ ，求 $ a $ 的取值范围.

注：两个猜想都判断、证明或说明理由，仅按第一个解答计分.

答案：

（1）【解】若选 $ \mathrm{①}(x\otimes y)\otimes z=x\otimes (y\otimes z) $ ,猜想正确,理由如下：

$ (x\otimes y)\otimes z= \lg ({10}^{x}+{10}^{y})\otimes z= \lg [{10}^{ \lg (10x+10y)}+{10}^{z}]= \lg ({10}^{x}+{10}^{y}+{10}^{z}) $ ,

$ x\otimes (y\otimes z)=x\otimes \lg ({10}^{y}+{10}^{z})= \lg [{10}^{x}+{10}^{ \lg (10y+10z)}]= \lg ({10}^{x}+{10}^{y}+{10}^{z}) $ ,

故 $ (x\otimes y)\otimes z=x\otimes (y\otimes z) $ .

若选 $ \mathrm{②}(x\otimes y)+z=(x+z)\otimes (y+z) $ ,猜想正确,理由如下：

$ (x\otimes y)+z= \lg ({10}^{x}+{10}^{y})+z $ ,

而 $ (x+z)\otimes (y+z)= \lg ({10}^{x+z}+{10}^{y+z})= \lg [({10}^{x}+{10}^{y})\cdot {10}^{z}]= \lg ({10}^{x}+{10}^{y})+z $ ,

故 $ (x\otimes y)+z=(x+z)\otimes (y+z) $ .

（2）【解】由题意可知 $ f(x)=(s+1)\otimes (s+3)-1- \lg 101= \lg ({10}^{s+1}+{10}^{s+3})-1- \lg 101 $

$ = \lg [{10}^{s+1}\cdot (1+{10}^{2})]-1- \lg 101=s+1+ \lg 101-1- \lg 101=s={ \log }_{a}[(x-2a)(x-4a)] $ ,

令 $ g(x)=(x-2a)(x-4a)={x}^{2}-6ax+8{a}^{2} $ ,其图象的对称轴为直线 $ x=3a $ ,

故 $ g(x) $ 在 $ (0,2a) $ 上单调递减.

因为 $ f(x) $ 在区间 $ [m,n] $ 上的值域为 $ [{ \log }_{a}n,{ \log }_{a}m] $ ,

故 $ { \log }_{a}n < { \log }_{a}m $ ,而 $ 0 < m < n $ ,故 $ 0 < a < 1 $ ,

此时 $ y={ \log }_{a}x $ 在 $ (0,+\mathrm{\infty }) $ 上单调递减,

所以 $ f(x)={ \log }_{a}g(x) $ 在 $ [m,n] $ 上单调递增,则 $ \begin{cases}f(m)={ \log }_{a}n,\\ f(n)={ \log }_{a}m,\end{cases} $

即 $ \begin{cases}{ \log }_{a}[(m-2a)(m-4a)]={ \log }_{a}n,\\ { \log }_{a}[(n-2a)(n-4a)]={ \log }_{a}m,\end{cases} $

即 $ \begin{cases}(m-2a)(m-4a)=n,\\ (n-2a)(n-4a)=m,\end{cases} $ 两式相减，整理得 $ {m}^{2}-{n}^{2}-6a(m-n)=-(m-n) $ ,

即 $ m+n-6a=-1 $ ,将 $ n=6a-m-1 $ 代入 $ (m-2a)(m-4a)=n $ ,

得 $ {m}^{2}-(6a-1)m+8{a}^{2}-6a+1=0 $ ,同理得 $ {n}^{2}-(6a-1)n+8{a}^{2}-6a+1=0 $ ,

即 $ m $ , $ n $ 是关于 $ x $ 的方程 $ {x}^{2}-(6a-1)x+8{a}^{2}-6a+1=0 $ 在 $ (0,2a) $ 上的两个不同的根.

令 $ ℎ(x)={x}^{2}-(6a-1)x+8{a}^{2}-6a+1 $ ,则 $ \begin{cases}ℎ(0)=8{a}^{2}-6a+1 > 0,\\ ℎ(2a)=-4a+1 > 0,\\ 0 < \dfrac{6a-1}{2} < 2a,\\ \mathrm{\Delta }={\left(6a-1\right) ^ {2}}-4(8{a}^{2}-6a+1) > 0,\end{cases} $

解得 $ \begin{cases}a < \dfrac{1}{4}\mathrm{或}a > \dfrac{1}{2},\\ a < \dfrac{1}{4},\\ \dfrac{1}{6} < a < \dfrac{1}{2},\\ a < \dfrac{-3-2\sqrt{3}}{2}\mathrm{或}a > \dfrac{-3+2\sqrt{3}}{2},\end{cases} $

故 $ a\in (\dfrac{2\sqrt{3}-3}{2},\dfrac{1}{4}) $ ,即 $ a $ 的取值范围为 $ (\dfrac{2\sqrt{3}-3}{2},\dfrac{1}{4}) $ .

解析：

专练2 开放题专练

一、刷素养