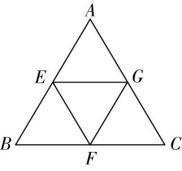
14.如图, $ E $ , $ F $ , $ G $ 依次是正三角形 $ ABC $ 的边 $ AB $ , $ BC $ , $ AC $ 的中点.
(1) 在以 $ A $ , $ B $ , $ C $ , $ E $ , $ F $ , $ G $ 为起点或终点的向量中,找出与向量 $ \overrightarrow {EF} $ 共线的向量;
(2) 在以 $ A $ , $ B $ , $ C $ 为起点,以 $ E $ , $ F $ , $ G $ 为终点的向量中,找出与向量 $ \overrightarrow {GF} $ 的模相等的向量;
(3) 在以 $ E $ , $ F $ , $ G $ 为起点,以 $ A $ , $ B $ , $ C $ 为终点的向量中,找出与向量 $ \overrightarrow {EG} $ 相等的向量.
答案:(1) 因为 $ E $ , $ F $ 分别为 $ AB $ , $ BC $ 的中点,所以 $ EF//AC $ ,且 $ EF=\dfrac{1}{2}AC $ ,所以与向量 $ \overrightarrow {EF} $ 共线的向量是 $ \overrightarrow {AG} $ , $ \overrightarrow {AC} $ , $ \overrightarrow {GA} $ , $ \overrightarrow {GC} $ , $ \overrightarrow {CG} $ , $ \overrightarrow {CA} $ , $ \overrightarrow {FE} $ .
(2) 因为 $ △ABC $ 是正三角形,所以 $ AB=AC=BC $ ,
又 $ E $ , $ F $ , $ G $ 依次是 $ △ABC $ 的边 $ AB $ , $ BC $ , $ AC $ 的中点,所以 $ AE=EB=GF=EF=GC=AG=BF=FC=EG $ ,
所以在以 $ A $ , $ B $ , $ C $ 为起点,以 $ E $ , $ F $ , $ G $ 为终点的向量中,
与向量 $ \overrightarrow {GF} $ 的模相等的向量为 $ \overrightarrow {AE} $ , $ \overrightarrow {AG} $ , $ \overrightarrow {BE} $ , $ \overrightarrow {BF} $ , $ \overrightarrow {CG} $ , $ \overrightarrow {CF} $ .
(3) 在以 $ E $ , $ F $ , $ G $ 为起点,以 $ A $ , $ B $ , $ C $ 为终点的向量中,与向量 $ \overrightarrow {EG} $ 相等的向量为 $ \overrightarrow {FC} $ .