第6.1节综合训练

一、刷能力

1．下列说法中正确的有（      ）

①在物理学中，作用力与反作用力是一对共线向量；

②温度有零上温度和零下温度，因此温度也是向量；

③方向为南偏西 $ {60}^{\circ } $ 的向量与北偏东 $ {60}^{\circ } $ 的向量是共线向量；

④平面上的数轴都是向量.

A．1个

B．2个

C．3个

D．4个

答案：B
解析：

既有大小又有方向的量称为向量,结合向量的概念可知②④错误,结合向量的概念以及共线向量的定义可知①③正确,故选 $ \mathrm{B} $ .

2．在菱形 $ ABCD $ 中， $ \mathrm{\angle }DAB={120}^{\circ } $ ，对角线 $ AC\cap BD=O $ ，给出以下结论：

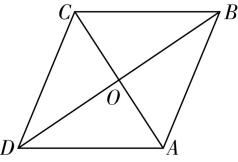
试题资源网 https://stzy.com

$ ①\overrightarrow {DO} $ 与 $ \overrightarrow {DB} $ 是平行向量；

$ ②\overrightarrow {DA} $ 与 $ \overrightarrow {BC} $ 是共线向量；

$ ③|\overrightarrow {DC}|=|\overrightarrow {AC}| $ ；

$ ④\overrightarrow {DO} $ 与 $ \overrightarrow {AB} $ 是共线向量.

其中正确结论的个数是（      ）

A．1

B．2

C．3

D．4

答案：C
解析：

对于①,因为 $ DO $ 和 $ DB $ 在同一条直线上,根据平行向量的定义,平行向量又称共线向量,方向相同或相反,①正确；

对于②,因为四边形 $ ABCD $ 是菱形,所以 $ AD//BC $ ,根据平行向量的定义,平行向量又称共线向量,方向相同或相反,②正确；

对于③,在菱形 $ ABCD $ 中, $ \mathrm{\angle }DAB={120}^{\circ } $ ,所以 $ △ACD $ 为等边三角形,则 $ AC=DC $ ,所以 $ |\overrightarrow {DC}|=|\overrightarrow {AC}| $ ,③正确；

对于④, $ DO $ 与 $ AB $ 不平行,所以 $ \overrightarrow {DO} $ 与 $ \overrightarrow {AB} $ 不共线,④错误.故选 $ \mathrm{C} $ .

3．已知平面向量 $ \boldsymbol{a} $ ， $ \boldsymbol{b} $ ，则“ $ \boldsymbol{a}=\boldsymbol{b} $ ”是“ $ |\boldsymbol{a}|=|\boldsymbol{b}| $ ”的（      ）

A．充分不必要条件

B．必要不充分条件

C．充要条件

D．既不充分也不必要条件

答案：A
解析：

若 $ \boldsymbol{a}=\boldsymbol{b} $ ,则 $ |\boldsymbol{a}|=|\boldsymbol{b}| $ ,反过来,若 $ |\boldsymbol{a}|=|\boldsymbol{b}| $ ,两个向量的方向不确定,不能推出 $ \boldsymbol{a}=\boldsymbol{b} $ ,所以“ $ \boldsymbol{a}=\boldsymbol{b} $ ”是“ $ |\boldsymbol{a}|=|\boldsymbol{b}| $ ”的充分不必要条件.故选 $ \mathrm{A} $ .

4．已知点 $ O $ 在 $ △ABC $ 所在平面内，且满足 $ |\overrightarrow {OA}|=|\overrightarrow {OB}|=|\overrightarrow {OC}| $ ，则点 $ O $ 是 $ △ABC $ 的（      ）

A．外心

B．内心

C．垂心

D．重心

答案：A
解析：

因为 $ |\overrightarrow {OA}|=|\overrightarrow {OB}|=|\overrightarrow {OC}| $ ,即点 $ O $ 到点 $ A $ , $ B $ , $ C $ 的距离相等,所以点 $ O $ 是 $ △ABC $ 的外心,故选 $ \mathrm{A} $ .

5．在四边形 $ ABCD $ 中， $ AC $ 与 $ BD $ 交于点 $ O $ ，且 $ \overrightarrow {AO}=\overrightarrow {OC} $ ， $ \overrightarrow {BO}=\overrightarrow {OD} $ ， $ |\overrightarrow {AC}|=|\overrightarrow {BD}| $ ，则 （      ）

A． $ AC\perp BD $

B．四边形 $ ABCD $ 是梯形

C．四边形 $ ABCD $ 是菱形

D．四边形 $ ABCD $ 是矩形

答案：D
解析：

由 $ \overrightarrow {AO}=\overrightarrow {OC} $ , $ \overrightarrow {BO}=\overrightarrow {OD} $ , $ |\overrightarrow {AC}|=|\overrightarrow {BD}| $ ,知四边形 $ ABCD $ 的对角线互相平分且相等,所以四边形 $ ABCD $ 为矩形.故选 $ \mathrm{D} $ .

6．如图所示， $ O $ 为正方形 $ ABCD $ 对角线的交点，四边形 $ OAED $ ， $ OCFB $ 都是正方形，根据图中所标出的向量回答下列问题.

试题资源网 https://stzy.com

（1） 分别写出与 $ \overrightarrow {AO} $ ， $ \overrightarrow {BO} $ 相等的向量；

（2） 写出与 $ \overrightarrow {AO} $ 共线的向量；

（3） 写出与 $ \overrightarrow {AO} $ 模相等的向量.

答案：

（1） 【解】 $ \overrightarrow {AO}=\overrightarrow {BF} $ , $ \overrightarrow {BO}=\overrightarrow {AE} $ .

（2） 与 $ \overrightarrow {AO} $ 共线的向量有 $ \overrightarrow {CO} $ , $ \overrightarrow {BF} $ , $ \overrightarrow {DE} $ .

（3） 与 $ \overrightarrow {AO} $ 模相等的向量有 $ \overrightarrow {CO} $ , $ \overrightarrow {BF} $ , $ \overrightarrow {DE} $ , $ \overrightarrow {AE} $ , $ \overrightarrow {BO} $ , $ \overrightarrow {DO} $ , $ \overrightarrow {CF} $ .

解析：

7．如图所示的方格纸是由若干个边长为1的小正方形拼在一起组成的，方格纸中有两个定点 $ A $ ， $ B $ ，点 $ C $ 为小正方形的顶点，且 $ |\overrightarrow {AC}|=\sqrt{5} $ .

试题资源网 https://stzy.com

（1） 画出所有满足条件的向量 $ \overrightarrow {AC} $ ；

（2） 求 $ |\overrightarrow {BC}| $ 的最大值与最小值.

答案：

（1） 【解】画出所有满足条件的向量 $ \overrightarrow {AC} $ ,即 $ {\overrightarrow {AC}}_{i}(i=1,2,\cdots ,8) $ ,如图所示.

试题资源网 https://stzy.com

（2） 由（1）所画的图知,当点 $ C $ 位于点 $ {C}_{1} $ 或 $ {C}_{2} $ 的位置时, $ |\overrightarrow {BC}| $ 取得最小值 $ \sqrt{{1}^{2}+{2}^{2}}=\sqrt{5} $ ；

当点 $ C $ 位于点 $ {C}_{5} $ 或 $ {C}_{6} $ 的位置时, $ |\overrightarrow {BC}| $ 取得最大值 $ \sqrt{{4}^{2}+{5}^{2}}=\sqrt{41} $ ,

故 $ |\overrightarrow {BC}| $ 的最大值为 $ \sqrt{41} $ ,最小值为 $ \sqrt{5} $ .

解析：