6.2.1 向量的加法运算+6.2.2 向量的减法运算
一、刷基础
1.向量 $ \overrightarrow {AB}+\overrightarrow {BO}+\overrightarrow {OM}+\overrightarrow {MB}+\overrightarrow {BC}= $ ( )
A. $ \overrightarrow {AC} $
B. $ \overrightarrow {AB} $
C. $ \overrightarrow {BC} $
D. $ \overrightarrow {AM} $
答案:A
解析:根据平面向量加法的三角形法则,可得 $ \overrightarrow {AB}+\overrightarrow {BO}+\overrightarrow {OM}+\overrightarrow {MB}+\overrightarrow {BC}=\overrightarrow {AC} $ .故选 $ \mathrm{A} $ .
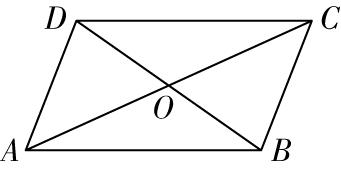
2.如图,在平行四边形 $ ABCD $ 中, $ \overrightarrow {AC}+\overrightarrow {BA}+\overrightarrow {DA}= $ ( )
A. $ 0 $
B. $ \overrightarrow {OA} $
C. $ \overrightarrow {AD} $
D. $ \overrightarrow {AC} $
答案:A
解析:依题意, $ \overrightarrow {AC}=\overrightarrow {AB}+\overrightarrow {AD} $ ,所以 $ \overrightarrow {AC}+\overrightarrow {BA}+\overrightarrow {DA}=\overrightarrow {AB}+\overrightarrow {AD}+\overrightarrow {BA}+\overrightarrow {DA}=\overrightarrow {AB}+\overrightarrow {BA}+\overrightarrow {AD}+\overrightarrow {DA}=0 $ .故选 $ \mathrm{A} $ .
3.对于任意一个四边形 $ ABCD $ ,下列式子不能化简为 $ \overrightarrow {BC} $ 的有( )
A. $ \overrightarrow {BA}+\overrightarrow {AD}+\overrightarrow {DC} $
B. $ \overrightarrow {BD}+\overrightarrow {DA}+\overrightarrow {AC} $
C. $ \overrightarrow {AB}+\overrightarrow {BD}+\overrightarrow {DC} $
D. $ \overrightarrow {DC}+\overrightarrow {BA}+\overrightarrow {AD} $
答案:C
解析:对于 $ \mathrm{A} $ , $ \overrightarrow {BA}+\overrightarrow {AD}+\overrightarrow {DC}=\overrightarrow {BD}+\overrightarrow {DC}=\overrightarrow {BC} $ ;
对于 $ \mathrm{B} $ , $ \overrightarrow {BD}+\overrightarrow {DA}+\overrightarrow {AC}=\overrightarrow {BA}+\overrightarrow {AC}=\overrightarrow {BC} $ ;
对于 $ \mathrm{C} $ , $ \overrightarrow {AB}+\overrightarrow {BD}+\overrightarrow {DC}=\overrightarrow {AD}+\overrightarrow {DC}=\overrightarrow {AC} $ ;
对于 $ \mathrm{D} $ , $ \overrightarrow {DC}+\overrightarrow {BA}+\overrightarrow {AD}=\overrightarrow {DC}+\overrightarrow {BD}=\overrightarrow {BD}+\overrightarrow {DC}=\overrightarrow {BC} $ .
故选 $ \mathrm{C} $ .
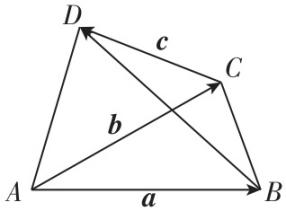
4.如图,向量 $ \overrightarrow {AB}=\boldsymbol{a} $ , $ \overrightarrow {AC}=\boldsymbol{b} $ , $ \overrightarrow {CD}=\boldsymbol{c} $ ,则向量 $ \overrightarrow {BD} $ 可以表示为( )
A. $ \boldsymbol{a}+\boldsymbol{b}-\boldsymbol{c} $
B. $ \boldsymbol{a}-\boldsymbol{b}+\boldsymbol{c} $
C. $ \boldsymbol{b}-\boldsymbol{a}+\boldsymbol{c} $
D. $ \boldsymbol{b}-\boldsymbol{a}-\boldsymbol{c} $
答案:C
解析:依题意得, $ \overrightarrow {BD}=\overrightarrow {AD}-\overrightarrow {AB}=\overrightarrow {AC}+\overrightarrow {CD}-\overrightarrow {AB} $ ,即 $ \overrightarrow {BD}=\boldsymbol{b}-\boldsymbol{a}+\boldsymbol{c} $ .故选 $ \mathrm{C} $ .
5.化简以下各式,结果不是零向量的为( )
A. $ \overrightarrow {AB}+\overrightarrow {BC}+\overrightarrow {CA} $
B. $ \overrightarrow {AB}+\overrightarrow {AC}-\overrightarrow {BD}+\overrightarrow {CD} $
C. $ \overrightarrow {OA}-\overrightarrow {OD}+\overrightarrow {AD} $
D. $ \overrightarrow {NQ}+\overrightarrow {QP}+\overrightarrow {MN}-\overrightarrow {MP} $
答案:B
解析:对于 $ \mathrm{A} $ : $ \overrightarrow {AB}+\overrightarrow {BC}+\overrightarrow {CA}=0 $ ,故 $ \mathrm{A} $ 正确;
对于 $ \mathrm{B} $ : $ \overrightarrow {AB}+\overrightarrow {AC}-\overrightarrow {BD}+\overrightarrow {CD}=\overrightarrow {AB}+\overrightarrow {AC}+\overrightarrow {DB}+\overrightarrow {CD} $
$ =\overrightarrow {AC}+\overrightarrow {CD}+\overrightarrow {DB}+\overrightarrow {AB}=\overrightarrow {AB}+\overrightarrow {AB}=2\overrightarrow {AB} $ ,故 $ \mathrm{B} $ 错误;
对于 $ \mathrm{C} $ : $ \overrightarrow {OA}-\overrightarrow {OD}+\overrightarrow {AD}=\overrightarrow {DA}+\overrightarrow {AD}=0 $ ,故 $ \mathrm{C} $ 正确;
对于 $ \mathrm{D} $ : $ \overrightarrow {NQ}+\overrightarrow {QP}+\overrightarrow {MN}-\overrightarrow {MP}=\overrightarrow {NQ}+\overrightarrow {QP}+\overrightarrow {MN}+\overrightarrow {PM}=\overrightarrow {NQ}+\overrightarrow {QP}+\overrightarrow {PM}+\overrightarrow {MN}=0 $ ,故 $ \mathrm{D} $ 正确.
故选 $ \mathrm{B} $ .
6.在四边形 $ ABCD $ 中, $ O $ 为任意一点,若 $ \overrightarrow {OA}-\overrightarrow {OB}+\overrightarrow {OC}-\overrightarrow {OD}=0 $ ,则四边形 $ ABCD $ 一定为( )
A.矩形
B.菱形
C.等腰梯形
D.平行四边形
答案:D
解析:因为 $ \overrightarrow {OA}-\overrightarrow {OB}+\overrightarrow {OC}-\overrightarrow {OD}=0 $ ,所以 $ \overrightarrow {BA}+\overrightarrow {DC}=0 $ ,即 $ \overrightarrow {AB}=\overrightarrow {DC} $ ,
可知 $ AB $ , $ CD $ 两边平行且相等,所以四边形 $ ABCD $ 是平行四边形.
但没有足够条件判断四边形 $ ABCD $ 是否为矩形或菱形.故选 $ \mathrm{D} $ .
7.已知 $ \overrightarrow {OA}=\boldsymbol{a} $ , $ \overrightarrow {OB}=\boldsymbol{b} $ , $ \overrightarrow {OC}=\boldsymbol{c} $ , $ \overrightarrow {OD}=\boldsymbol{d} $ , $ \overrightarrow {OE}=\boldsymbol{e} $ , $ \overrightarrow {OF}=\boldsymbol{f} $ ,试用 $ \boldsymbol{a} $ , $ \boldsymbol{b} $ , $ \boldsymbol{c} $ , $ \boldsymbol{d} $ , $ \boldsymbol{e} $ , $ \boldsymbol{f} $ 表示下列各式:
(1) $ \overrightarrow {AD}-\overrightarrow {AB} $ ;
(2) $ \overrightarrow {AB}+\overrightarrow {CF} $ ;
(3) $ \overrightarrow {EF}-\overrightarrow {CF} $ .
答案:(1) 【解】 $ \overrightarrow {AD}-\overrightarrow {AB}=(\overrightarrow {OD}-\overrightarrow {OA})-(\overrightarrow {OB}-\overrightarrow {OA})=\boldsymbol{d}-\boldsymbol{a}-\boldsymbol{b}+\boldsymbol{a}=\boldsymbol{d}-\boldsymbol{b} $ .
(2) $ \overrightarrow {AB}+\overrightarrow {CF}=(\overrightarrow {OB}-\overrightarrow {OA})+(\overrightarrow {OF}-\overrightarrow {OC})=\boldsymbol{b}-\boldsymbol{a}+\boldsymbol{f}-\boldsymbol{c} $ .
(3) $ \overrightarrow {EF}-\overrightarrow {CF}=(\overrightarrow {OF}-\overrightarrow {OE})-(\overrightarrow {OF}-\overrightarrow {OC})=\boldsymbol{f}-\boldsymbol{e}-\boldsymbol{f}+\boldsymbol{c}=\boldsymbol{c}-\boldsymbol{e} $ .
解析:
8.在 $ △ABC $ 中,若 $ |\overrightarrow {AB}|=|\overrightarrow {AC}|=|\overrightarrow {AB}-\overrightarrow {AC}| $ ,则 $ △ABC $ 的形状为( )
A.等边三角形
B.等腰(非等边)三角形
C.直角三角形
D.等腰直角三角形
答案:A
解析:因为 $ |\overrightarrow {AB}-\overrightarrow {AC}|=|\overrightarrow {CB}| $ , $ |\overrightarrow {AB}|=|\overrightarrow {AC}|=|\overrightarrow {AB}-\overrightarrow {AC}| $ ,所以 $ |\overrightarrow {AB}|=|\overrightarrow {AC}|=|\overrightarrow {CB}| $ ,所以 $ △ABC $ 为等边三角形.故选 $ \mathrm{A} $ .
9.设 $ \boldsymbol{a} $ 表示“向东走 $ 6\mathrm{k}\mathrm{m} $ ”, $ \boldsymbol{b} $ 表示“向南走 $ 3\mathrm{k}\mathrm{m} $ ”,则 $ \boldsymbol{b}-\boldsymbol{a}+\boldsymbol{b} $ 所表示的意义为( )
A. 向东南走 $ 6\sqrt{2}\mathrm{k}\mathrm{m} $
B. 向东南走 $ 3\sqrt{6}\mathrm{k}\mathrm{m} $
C. 向西南走 $ 6\sqrt{2}\mathrm{k}\mathrm{m} $
D. 向西南走 $ 3\sqrt{6}\mathrm{k}\mathrm{m} $
答案:C
解析:如图,分别作出 $ \stackrel{\to }{OA}=\boldsymbol{a} $ , $ \stackrel{\to }{OC}=\boldsymbol{b} $ , $ \stackrel{\to }{CB}=\boldsymbol{b} $ ,则利用向量加法的交换律可得 $ \boldsymbol{b}-\boldsymbol{a}+\boldsymbol{b}=\boldsymbol{b}+\boldsymbol{b}-\boldsymbol{a} $ ,故 $ \stackrel{\to }{AB}=\boldsymbol{b}+\boldsymbol{b}-\boldsymbol{a} $ .
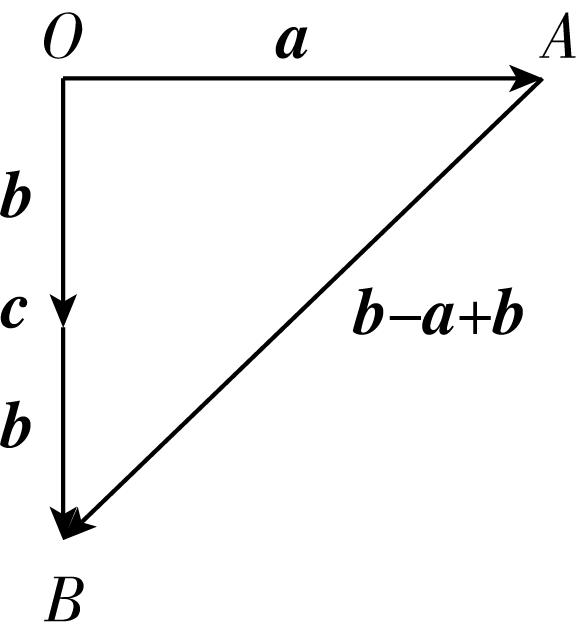
易知 $ △OAB $ 为等腰直角三角形,故 $ \mathrm{\angle }OAB={45}^{\circ } $ ,且 $ |\stackrel{\to }{AB}|=6\sqrt{2} $ ,
于是 $ \boldsymbol{b}-\boldsymbol{a}+\boldsymbol{b} $ 所表示的意义为向西南走 $ 6\sqrt{2}\mathrm{k}\mathrm{m} $ .
故选C.
10.已知 $ |\overrightarrow {AB}|=6 $ , $ |\overrightarrow {AC}|=3 $ ,则 $ |\overrightarrow {BC}| $ 的取值范围是( )
A. $ [3,6] $
B. $ (3,6) $
C. $ [3,9] $
D. $ (3,9) $
答案:C
解析:由题意得 $ \overrightarrow {BC}=\overrightarrow {AC}-\overrightarrow {AB} $ ,所以 $ |\overrightarrow {BC}|=|\overrightarrow {AC}-\overrightarrow {AB}| $ ,所以 $ ||\overrightarrow {AC}|-|\overrightarrow {AB}||\leqslant |\overrightarrow {AC}-\overrightarrow {AB}|\leqslant |\overrightarrow {AC}|+|\overrightarrow {AB}| $ ,则 $ 3\leqslant |\overrightarrow {BC}|\leqslant 9 $ ,故 $ \mathrm{C} $ 正确.故选 $ \mathrm{C} $ .
11.若 $ \boldsymbol{a} $ , $ \boldsymbol{b} $ 是非零向量,则“ $ |\boldsymbol{a}|=|\boldsymbol{b}| $ ”是“ $ |\boldsymbol{a}+\boldsymbol{b}|=|\boldsymbol{a}-\boldsymbol{b}| $ ”的( )
A.充分不必要条件
B.必要不充分条件
C.充要条件
D.既不充分也不必要条件
答案:D
解析:如图作 $ ▱ABCD $ ,设 $ \overrightarrow {AB}=\boldsymbol{a} $ , $ \overrightarrow {AD}=\boldsymbol{b} $ ,
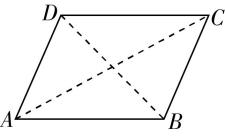
由向量加法的平行四边形法则知:由 $ |\boldsymbol{a}|=|\boldsymbol{b}| $ 可得 $ ▱ABCD $ 是菱形,
因为菱形的对角线不一定相等,所以 $ |\boldsymbol{a}+\boldsymbol{b}|=|\boldsymbol{a}-\boldsymbol{b}| $ 不一定成立,即充分性不成立;
又由 $ |\boldsymbol{a}+\boldsymbol{b}|=|\boldsymbol{a}-\boldsymbol{b}| $ 可得 $ ▱ABCD $ 是矩形,因为矩形的一组邻边不一定相等,
所以 $ |\boldsymbol{a}|=|\boldsymbol{b}| $ 也不一定成立,即必要性不成立.
故“ $ |\boldsymbol{a}|=|\boldsymbol{b}| $ ”是“ $ |\boldsymbol{a}+\boldsymbol{b}|=|\boldsymbol{a}-\boldsymbol{b}| $ ”的既不充分也不必要条件.
故选 $ \mathrm{D} $ .
二、刷提升
1.下列说法:
①如果非零向量 $ \boldsymbol{a} $ 与 $ \boldsymbol{b} $ 的方向相同或相反,那么 $ \boldsymbol{a}+\boldsymbol{b} $ 的方向必与 $ \boldsymbol{a} $ , $ \boldsymbol{b} $ 之一的方向相同;
②在 $ △ABC $ 中,必有 $ \overrightarrow {AB}+\overrightarrow {BC}+\overrightarrow {CA}=0 $ ;
③若 $ \overrightarrow {AB}+\overrightarrow {BC}+\overrightarrow {CA}=0 $ ,则 $ A $ , $ B $ , $ C $ 为一个三角形的三个顶点;
④若 $ \boldsymbol{a} $ , $ \boldsymbol{b} $ 均为非零向量,则 $ |\boldsymbol{a}+\boldsymbol{b}| $ 与 $ |\boldsymbol{a}|+|\boldsymbol{b}| $ 一定相等.
其中正确说法的个数为( )
A.0
B.1
C.2
D.3
答案:B
解析:①错误,若 $ \boldsymbol{a}+\boldsymbol{b}=0 $ ,其方向是任意的;②正确;③错误, $ A $ , $ B $ , $ C $ 三点共线时也可满足;④错误, $ |\boldsymbol{a}+\boldsymbol{b}|\leqslant |\boldsymbol{a}|+|\boldsymbol{b}| $ .
2.下列向量的运算结果不正确的是( )
A. $ \overrightarrow {AB}+\overrightarrow {BC}=\overrightarrow {AC} $
B. $ \overrightarrow {AB}-\overrightarrow {AD}=\overrightarrow {DB} $
C. $ \overrightarrow {AB}-(\overrightarrow {AD}+\overrightarrow {DC})=\overrightarrow {BC} $
D. $ \overrightarrow {OA}-\overrightarrow {OD}+\overrightarrow {AD}=0 $
答案:C
解析:由 $ \overrightarrow {AB}+\overrightarrow {BC}=\overrightarrow {AC} $ ,故 $ \mathrm{A} $ 正确;
$ \overrightarrow {AB}-\overrightarrow {AD}=\overrightarrow {DB} $ ,故 $ \mathrm{B} $ 正确;
$ \overrightarrow {AB}-(\overrightarrow {AD}+\overrightarrow {DC})=\overrightarrow {AB}-\overrightarrow {AC}=\overrightarrow {CB} $ ,故 $ \mathrm{C} $ 错误;
$ \overrightarrow {OA}-\overrightarrow {OD}+\overrightarrow {AD}=\overrightarrow {DA}+\overrightarrow {AD}=0 $ ,故 $ \mathrm{D} $ 正确.
故选 $ \mathrm{C} $ .
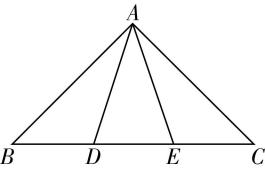
3.等腰三角形 $ ABC $ 中, $ AB=AC $ , $ D $ , $ E $ 在边 $ BC $ 上,满足 $ BD=DE=EC $ ,则下列各式中正确的是( )
A. $ \overrightarrow {AD}=\overrightarrow {AE} $
B. $ \overrightarrow {BD}=\overrightarrow {CE} $
C. $ \overrightarrow {AB}+\overrightarrow {AE}=\overrightarrow {AC}+\overrightarrow {AD} $
D. $ \overrightarrow {AB}+\overrightarrow {AC}=\overrightarrow {AD}+\overrightarrow {AE} $
答案:D
解析:对于 $ \mathrm{A} $ ,如图, $ \overrightarrow {AD} $ 与 $ \overrightarrow {AE} $ 方向不同,故 $ \mathrm{A} $ 错误;
对于 $ \mathrm{B} $ , $ \overrightarrow {BD} $ 与 $ \overrightarrow {CE} $ 方向相反,故 $ \mathrm{B} $ 错误;
对于 $ \mathrm{C} $ ,因为 $ D $ , $ E $ 在边 $ BC $ 上,满足 $ BD=DE=EC $ ,
所以 $ \overrightarrow {AB}+\overrightarrow {AE}=2\overrightarrow {AD} $ , $ \overrightarrow {AC}+\overrightarrow {AD}=2\overrightarrow {AE} $ ,由 $ \mathrm{A} $ 项知 $ \overrightarrow {AD} $ 与 $ \overrightarrow {AE} $ 不相等,故 $ \mathrm{C} $ 错误;
对于 $ \mathrm{D} $ ,由图知, $ \overrightarrow {AB}+\overrightarrow {AC}=\overrightarrow {AD}+\overrightarrow {DB}+\overrightarrow {AE}+\overrightarrow {EC}=\overrightarrow {AD}+\overrightarrow {AE}+(\overrightarrow {DB}+\overrightarrow {EC}) $ ,
因为 $ \overrightarrow {DB}+\overrightarrow {EC}=0 $ ,所以 $ \overrightarrow {AB}+\overrightarrow {AC}=\overrightarrow {AD}+\overrightarrow {AE} $ ,即 $ \mathrm{D} $ 正确.故选 $ \mathrm{D} $ .
4.已知向量 $ \boldsymbol{a} $ , $ \boldsymbol{b} $ 满足 $ |\boldsymbol{a}|=1 $ , $ |\boldsymbol{a}-\boldsymbol{b}|=\dfrac{1}{2} $ ,则 $ |\boldsymbol{b}| $ 的取值范围为( )
A. $ (\dfrac{\sqrt{3}}{2},\dfrac{3}{2}) $
B. $ [\dfrac{\sqrt{3}}{2},1] $
C. $ [\dfrac{\sqrt{3}}{2},\dfrac{3}{2}] $
D. $ [\dfrac{1}{2},\dfrac{3}{2}] $
答案:D
解析:由 $ \boldsymbol{b}=\boldsymbol{a}-(\boldsymbol{a}-\boldsymbol{b}) $ ,可得 $ |\boldsymbol{b}|=|\boldsymbol{a}-(\boldsymbol{a}-\boldsymbol{b})|\leqslant |\boldsymbol{a}|+|\boldsymbol{a}-\boldsymbol{b}|=\dfrac{3}{2} $ ,当且仅当 $ \boldsymbol{a} $ , $ \boldsymbol{a}-\boldsymbol{b} $ 反向共线时,等号成立; $ |\boldsymbol{b}|=|\boldsymbol{a}-(\boldsymbol{a}-\boldsymbol{b})|\geqslant ||\boldsymbol{a}|-|\boldsymbol{a}-\boldsymbol{b}||=\dfrac{1}{2} $ ,当且仅当 $ \boldsymbol{a} $ , $ \boldsymbol{a}-\boldsymbol{b} $ 同向共线时,等号成立.
所以 $ |\boldsymbol{b}| $ 的取值范围为 $ [\dfrac{1}{2},\dfrac{3}{2}] $ .故选 $ \mathrm{D} $ .
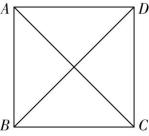
5.在平行四边形 $ ABCD $ 中, $ |\overrightarrow {AB}+\overrightarrow {AD}|=|\overrightarrow {AB}-\overrightarrow {AD}|=4 $ ,且 $ \mathrm{\angle }BAC=\mathrm{\angle }CAD $ ,则平行四边形 $ ABCD $ 的面积为 .
解析:在平行四边形 $ ABCD $ 中, $ \overrightarrow {AB}+\overrightarrow {AD}=\overrightarrow {AC} $ , $ \overrightarrow {AB}-\overrightarrow {AD}=\overrightarrow {DB} $ ,
因为 $ |\overrightarrow {AB}+\overrightarrow {AD}|=|\overrightarrow {AB}-\overrightarrow {AD}|=4 $ ,所以 $ |\overrightarrow {AC}|=|\overrightarrow {DB}|=4 $ ,所以四边形 $ ABCD $ 为矩形.
又 $ \mathrm{\angle }BAC=\mathrm{\angle }CAD $ ,所以四边形 $ ABCD $ 为正方形,所以四边形 $ ABCD $ 的面积为 $ \dfrac{1}{2}×4×4=8 $ .
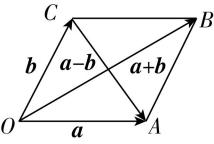
6.已知非零向量 $ \boldsymbol{a} $ , $ \boldsymbol{b} $ 满足 $ |\boldsymbol{a}|=|\boldsymbol{b}|=|\boldsymbol{a}-\boldsymbol{b}| $ ,作 $ \overrightarrow {OA}=\boldsymbol{a} $ , $ \overrightarrow {OB}=\boldsymbol{a}+\boldsymbol{b} $ ,则 $ \mathrm{\angle }AOB= $ .
解析:构造如图所示的平行四边形 $ OABC $ , $ \overrightarrow {OA}=\boldsymbol{a} $ , $ \overrightarrow {OB}=\boldsymbol{a}+\boldsymbol{b} $ ,则 $ \overrightarrow {OC}=\boldsymbol{b} $ , $ \overrightarrow {CA}=\boldsymbol{a}-\boldsymbol{b} $ ,又 $ |\boldsymbol{a}|=|\boldsymbol{b}|=|\boldsymbol{a}-\boldsymbol{b}| $ ,则 $ △AOC $ 为正三角形,故 $ \mathrm{\angle }COA={60}^{\circ } $ ,易知平行四边形 $ OABC $ 为菱形,故 $ OB $ 平分 $ \mathrm{\angle }COA $ ,则 $ \mathrm{\angle }AOB={30}^{\circ } $ .
7.在 $ △ABC $ 中, $ \mathrm{\angle }C={90}^{\circ } $ , $ AC=BC $ ,则下列哪几个等式是成立的?
(1) $ |\overrightarrow {CA}-\overrightarrow {CB}|=|\overrightarrow {CA}+\overrightarrow {CB}| $ ;
(2) $ |\overrightarrow {AB}-\overrightarrow {AC}|=|\overrightarrow {BA}-\overrightarrow {BC}| $ ;
(3) $ |\overrightarrow {CA}-\overrightarrow {BA}|=|\overrightarrow {CB}-\overrightarrow {AB}| $ ;
(4) $ |\overrightarrow {CA}+\overrightarrow {CB}{|}^{2}=|\overrightarrow {AB}-\overrightarrow {AC}{|}^{2}=|\overrightarrow {BA}-\overrightarrow {CA}{|}^{2} $ .
答案:【解】如图,分别作 $ AC $ , $ CB $ 的平行线,交于点 $ D $ ,因为在 $ △ABC $ 中, $ AC\perp BC $ , $ AC=BC $ ,
所以四边形 $ ACBD $ 是正方形.
(1) 因为 $ \overrightarrow {CA}-\overrightarrow {CB}=\overrightarrow {BA} $ , $ \overrightarrow {CA}+\overrightarrow {CB}=\overrightarrow {CD} $ ,所以 $ |\overrightarrow {CA}-\overrightarrow {CB}|=|\overrightarrow {BA}| $ , $ |\overrightarrow {CA}+\overrightarrow {CB}|=|\overrightarrow {CD}| $ ,
因为 $ |\overrightarrow {BA}|=|\overrightarrow {CD}| $ ,所以 $ |\overrightarrow {CA}-\overrightarrow {CB}|=|\overrightarrow {CA}+\overrightarrow {CB}| $ ,故等式(1)成立.
(2) 因为 $ \overrightarrow {AB}-\overrightarrow {AC}=\overrightarrow {CB} $ , $ \overrightarrow {BA}-\overrightarrow {BC}=\overrightarrow {CA} $ ,
所以 $ |\overrightarrow {AB}-\overrightarrow {AC}|=|\overrightarrow {CB}| $ , $ |\overrightarrow {BA}-\overrightarrow {BC}|=|\overrightarrow {CA}| $ ,因为 $ |\overrightarrow {CB}|=|\overrightarrow {CA}| $ ,
所以 $ |\overrightarrow {AB}-\overrightarrow {AC}|=|\overrightarrow {BA}-\overrightarrow {BC}| $ ,故等式(2)成立.
(3) 因为 $ \overrightarrow {CA}-\overrightarrow {BA}=\overrightarrow {CA}+\overrightarrow {AB}=\overrightarrow {CB} $ , $ \overrightarrow {CB}-\overrightarrow {AB}=\overrightarrow {CB}+\overrightarrow {BA}=\overrightarrow {CA} $ ,
所以 $ |\overrightarrow {CA}-\overrightarrow {BA}|=|\overrightarrow {CB}| $ , $ |\overrightarrow {CB}-\overrightarrow {AB}|=|\overrightarrow {CA}| $ ,因为 $ |\overrightarrow {CB}|=|\overrightarrow {CA}| $ ,所以 $ |\overrightarrow {CA}-\overrightarrow {BA}|=|\overrightarrow {CB}-\overrightarrow {AB}| $ ,
故等式(3)成立.
(4) 因为 $ \overrightarrow {CA}+\overrightarrow {CB}=\overrightarrow {CD} $ , $ \overrightarrow {AB}-\overrightarrow {AC}=\overrightarrow {CB} $ , $ \overrightarrow {BA}-\overrightarrow {CA}=\overrightarrow {BA}+\overrightarrow {AC}=\overrightarrow {BC} $ ,
所以 $ |\overrightarrow {CA}+\overrightarrow {CB}|=|\overrightarrow {CD}| $ , $ |\overrightarrow {AB}-\overrightarrow {AC}|=|\overrightarrow {CB}| $ , $ |\overrightarrow {BA}-\overrightarrow {CA}|=|\overrightarrow {BC}| $ ,
因为 $ |\overrightarrow {CD}|\ne |\overrightarrow {CB}|=|\overrightarrow {BC}| $ ,所以 $ |\overrightarrow {CA}+\overrightarrow {CB}|\ne |\overrightarrow {AB}-\overrightarrow {AC}|=|\overrightarrow {BA}-\overrightarrow {CA}| $ ,
所以 $ |\overrightarrow {CA}+\overrightarrow {CB}{|}^{2}\ne |\overrightarrow {AB}-\overrightarrow {AC}{|}^{2}=|\overrightarrow {BA}-\overrightarrow {CA}{|}^{2} $ ,故等式(4)不成立.
综上,等式 $ (1)(2)(3) $ 成立,等式(4)不成立.

解析:
8.已知某人在静水中游泳的速度的大小为 $ 4\sqrt{3}\mathrm{k}\mathrm{m}/\mathrm{h} $ ,河水的流速的大小为 $ 4\mathrm{k}\mathrm{m}/\mathrm{h} $ ,现此人在河中游泳.
(1) 如果他垂直游向河对岸,那么他实际沿什么方向前进?实际前进的速度的大小为多少?
(2) 他必须朝哪个方向游,才能沿与水流垂直的方向前进?实际前进的速度的大小为多少?
参考数据: $ \tan {35.26}^{\circ }\approx \dfrac{\sqrt{2}}{2} $ .
答案:(1) 【解】如图①,用 $ \overrightarrow {OA} $ 表示河水的流速, $ \overrightarrow {OB} $ 表示该人在静水中游泳的速度.以 $ OA $ , $ OB $ 为邻边作平行四边形 $ OACB $ ,则 $ \overrightarrow {OC} $ 为此人游泳的实际速度.
在 $ \mathrm{R}\mathrm{t}△OAC $ 中, $ |\overrightarrow {OA}|=4 $ , $ |\overrightarrow {AC}|=|\overrightarrow {OB}|=4\sqrt{3} $ ,所以 $ |\overrightarrow {OC}|=\sqrt{|\overrightarrow {OA}{|}^{2}+|\overrightarrow {AC}{|}^{2}}=8 $ ,
$ \tan \mathrm{\angle }AOC=\dfrac{|\overrightarrow {AC}|}{|\overrightarrow {OA}|}=\sqrt{3} $ ,所以 $ \mathrm{\angle }AOC={60}^{\circ } $ .
故此人实际前进的速度的大小为 $ 8\mathrm{k}\mathrm{m}/\mathrm{h} $ ,方向与水流方向的夹角为 $ {60}^{\circ } $ .
(2) 如图②,用 $ \overrightarrow {O\prime A\prime } $ 表示河水的流速, $ \overrightarrow {O\prime B\prime } $ 表示此人在静水中游泳的速度,以 $ O\prime A\prime $ , $ O\prime B\prime $ 为邻边作平行四边形 $ O\prime A\prime C\prime B\prime $ ,则 $ \overrightarrow {O\prime C\prime } $ 表示此人实际游泳的速度.
所以有 $ |\overrightarrow {O\prime C\prime }|=\sqrt{|\overrightarrow {O\prime B\prime }{|}^{2}-|\overrightarrow {O\prime A\prime }{|}^{2}}=4\sqrt{2} $ ,所以 $ \tan \mathrm{\angle }B\prime O\prime C\prime =\dfrac{|\overrightarrow {B\prime C\prime }|}{|\overrightarrow {O\prime C\prime }|}=\dfrac{\sqrt{2}}{2} $ ,所以 $ \mathrm{\angle }B\prime O\prime C\prime \approx {35.26}^{\circ } $ .
故此人应朝与水流方向成 $ {125.26}^{\circ } $ 角的方向游,实际前进的速度的大小为 $ 4\sqrt{2}\mathrm{k}\mathrm{m}/\mathrm{h} $ .

解析:
9.已知非零向量 $ \boldsymbol{a} $ , $ \boldsymbol{b} $ 满足 $ |\boldsymbol{a}|=\sqrt{7}+1 $ , $ |\boldsymbol{b}|=\sqrt{7}-1 $ ,且 $ |\boldsymbol{a}-\boldsymbol{b}|=4 $ ,则 $ |\boldsymbol{a}+\boldsymbol{b}|= $ .
解析:如图所示,设 $ \overrightarrow {OA}=\boldsymbol{a} $ , $ \overrightarrow {OB}=\boldsymbol{b} $ ,则 $ |\overrightarrow {BA}|=|\boldsymbol{a}-\boldsymbol{b}| $ .
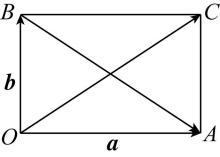
以 $ OA $ , $ OB $ 为邻边作平行四边形 $ OACB $ ,则 $ |\overrightarrow {OC}|=|\boldsymbol{a}+\boldsymbol{b}| $ .由于 $ (\sqrt{7}+1)^{2}+(\sqrt{7}-1)^{2}={4}^{2} $ ,故 $ |\overrightarrow {OA}{|}^{2}+|\overrightarrow {OB}{|}^{2}=|\overrightarrow {BA}{|}^{2} $ ,所以 $ △OAB $ 是直角三角形, $ \mathrm{\angle }AOB={90}^{\circ } $ ,从而 $ OA\perp OB $ ,所以平行四边形 $ OACB $ 是矩形.根据矩形的对角线相等得 $ |\overrightarrow {OC}|=|\overrightarrow {BA}|=4 $ ,即 $ |\boldsymbol{a}+\boldsymbol{b}|=4 $ .









