6.2.3 向量的数乘运算
一、刷基础
1.设向量 $ \boldsymbol{a} $ , $ \boldsymbol{b} $ , $ \boldsymbol{c} $ 满足 $ 5(\boldsymbol{a}-2\boldsymbol{b})-4(\boldsymbol{b}+3\boldsymbol{a})-\boldsymbol{c}=0 $ ,则 $ \boldsymbol{c}= $ ( )
A. $ -\boldsymbol{a}+22\boldsymbol{b} $
B. $ 7\boldsymbol{a}+14\boldsymbol{b} $
C. $ \boldsymbol{a}-22\boldsymbol{b} $
D. $ -7\boldsymbol{a}-14\boldsymbol{b} $
答案:D
解析:因为 $ 5(\boldsymbol{a}-2\boldsymbol{b})-4(\boldsymbol{b}+3\boldsymbol{a})-\boldsymbol{c}=-7\boldsymbol{a}-14\boldsymbol{b}-\boldsymbol{c}=0 $ ,所以 $ \boldsymbol{c}=-7\boldsymbol{a}-14\boldsymbol{b} $ .
故选 $ \mathrm{D} $ .
2.若 $ C $ 在线段 $ AB $ 上,且 $ \dfrac{AC}{CB}=\dfrac{3}{7} $ ,则( )
A. $ \overrightarrow {BC}=\dfrac{7}{13}\overrightarrow {BA} $
B. $ \overrightarrow {AC}=-\dfrac{3}{10}\overrightarrow {AB} $
C. $ \overrightarrow {BC}=\dfrac{7}{13}\overrightarrow {AB} $
D. $ \overrightarrow {AC}=-\dfrac{3}{10}\overrightarrow {BA} $
答案:D
解析: $ \because C $ 在线段 $ AB $ 上, $ \dfrac{AC}{CB}=\dfrac{3}{7} $ , $ \therefore AC=\dfrac{3}{10}AB $ , $ BC=\dfrac{7}{10}AB $ .
对于 $ \mathrm{A} $ , $ \overrightarrow {BC}=\dfrac{7}{10}\overrightarrow {BA} $ , $ \mathrm{A} $ 错误;
对于 $ \mathrm{B} $ , $ \overrightarrow {AC}=\dfrac{3}{10}\overrightarrow {AB} $ , $ \mathrm{B} $ 错误;
对于 $ \mathrm{C} $ , $ \overrightarrow {BC}=\dfrac{7}{10}\overrightarrow {BA}=-\dfrac{7}{10}\overrightarrow {AB} $ , $ \mathrm{C} $ 错误;
对于 $ \mathrm{D} $ , $ \overrightarrow {AC}=\dfrac{3}{10}\overrightarrow {AB}=-\dfrac{3}{10}\overrightarrow {BA} $ , $ \mathrm{D} $ 正确.故选 $ \mathrm{D} $ .
3.已知 $ D $ 为 $ △ABC $ 所在平面内的一点, $ 4\overrightarrow {AB}=3\overrightarrow {AD} $ , $ E $ 为 $ CD $ 的中点,则 $ \overrightarrow {AE}= $ ( )
A. $ \dfrac{4}{3}\overrightarrow {AB}+\dfrac{1}{2}\overrightarrow {AC} $
B. $ \dfrac{1}{2}\overrightarrow {AB}+\dfrac{4}{3}\overrightarrow {AC} $
C. $ \dfrac{2}{3}\overrightarrow {AB}+\dfrac{1}{2}\overrightarrow {AC} $
D. $ \dfrac{1}{2}\overrightarrow {AB}+\dfrac{2}{3}\overrightarrow {AC} $
答案:C
解析:由题意得 $ \overrightarrow {AE}=\overrightarrow {AC}+\overrightarrow {CE}=\overrightarrow {AC}+\dfrac{1}{2}\overrightarrow {CD}=\overrightarrow {AC}+\dfrac{1}{2}(\overrightarrow {AD}-\overrightarrow {AC})=\dfrac{1}{2}\overrightarrow {AC}+\dfrac{1}{2}\overrightarrow {AD} $
$ =\dfrac{1}{2}\overrightarrow {AC}+\dfrac{1}{2}×\dfrac{4}{3}\overrightarrow {AB}=\dfrac{2}{3}\overrightarrow {AB}+\dfrac{1}{2}\overrightarrow {AC} $ .故选 $ \mathrm{C} $ .
4.在平行四边形 $ ABCD $ 中, $ E $ 为 $ CD $ 的中点, $ BE $ 与对角线 $ AC $ 交于点 $ F $ ,记 $ \overrightarrow {AD}=\boldsymbol{a} $ , $ \overrightarrow {BF}=\boldsymbol{b} $ ,则 $ \overrightarrow {AB}= $ ( )
A. $ -\dfrac{1}{3}\boldsymbol{a}+\dfrac{2}{3}\boldsymbol{b} $
B. $ 2\boldsymbol{a}+3\boldsymbol{b} $
C. $ \dfrac{1}{3}\boldsymbol{a}+\dfrac{2}{3}\boldsymbol{b} $
D. $ 2\boldsymbol{a}-3\boldsymbol{b} $
答案:D
解析:由题意得, $ △ECF\sim △BAF $ ,所以 $ \dfrac{EF}{FB}=\dfrac{EC}{AB}=\dfrac{1}{2} $ ,所以 $ \overrightarrow {BF}=\dfrac{2}{3}\overrightarrow {BE} $ ,
所以 $ \overrightarrow {BF}=\dfrac{2}{3}(\overrightarrow {BC}+\overrightarrow {CE})=\dfrac{2}{3}(\overrightarrow {AD}-\dfrac{1}{2}\overrightarrow {AB})=\dfrac{2}{3}\overrightarrow {AD}-\dfrac{1}{3}\overrightarrow {AB} $ ,
所以 $ \overrightarrow {AB}=2\overrightarrow {AD}-3\overrightarrow {BF}=2\boldsymbol{a}-3\boldsymbol{b} $ .
故选 $ \mathrm{D} $ .
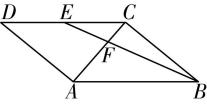
5.在四边形 $ ABCD $ 中,对角线 $ AC $ 与 $ BD $ 交于点 $ O $ .若 $ 2\overrightarrow {OA}+3\overrightarrow {OC}=2\overrightarrow {OD}+3\overrightarrow {OB} $ ,则四边形 $ ABCD $ 一定是( )
A.矩形
B.梯形
C.平行四边形
D.菱形
答案:B
解析: $ \because 2\overrightarrow {OA}+3\overrightarrow {OC}=2\overrightarrow {OD}+3\overrightarrow {OB} $ , $ \therefore 2(\overrightarrow {OA}-\overrightarrow {OD})=3(\overrightarrow {OB}-\overrightarrow {OC}) $ , $ \therefore 2\overrightarrow {DA}=3\overrightarrow {CB} $ , $ \therefore $ 四边形 $ ABCD $ 一定是梯形.故选 $ \mathrm{B} $ .
6.已知平面向量 $ \boldsymbol{a} $ , $ \boldsymbol{b} $ 是不共线的两个向量, $ \overrightarrow {AB}=\boldsymbol{a}+2\boldsymbol{b} $ , $ \overrightarrow {AC}=4\boldsymbol{a}-4\boldsymbol{b} $ , $ \overrightarrow {CD}=-\boldsymbol{a}+2\boldsymbol{b} $ ,则( )
A. $ A $ , $ B $ , $ C $ 三点共线
B. $ A $ , $ B $ , $ D $ 三点共线
C. $ A $ , $ C $ , $ D $ 三点共线
D. $ B $ , $ C $ , $ D $ 三点共线
答案:D
解析:由题意, $ \overrightarrow {AB}=\boldsymbol{a}+2\boldsymbol{b} $ , $ \overrightarrow {AC}=4\boldsymbol{a}-4\boldsymbol{b} $ , $ \overrightarrow {CD}=-\boldsymbol{a}+2\boldsymbol{b} $ ,
不存在唯一的实数 $ {\lambda }_{1} $ 使得 $ \overrightarrow {AB}={\lambda }_{1}\overrightarrow {AC} $ ,所以 $ A $ , $ B $ , $ C $ 三点不共线,故 $ \mathrm{A} $ 错误;
由于 $ \overrightarrow {AD}=\overrightarrow {AC}+\overrightarrow {CD}=4\boldsymbol{a}-4\boldsymbol{b}-\boldsymbol{a}+2\boldsymbol{b}=3\boldsymbol{a}-2\boldsymbol{b} $ ,
不存在唯一的实数 $ {\lambda }_{2} $ 使得 $ \overrightarrow {AB}={\lambda }_{2}\overrightarrow {AD} $ ,
不存在唯一的实数 $ {\lambda }_{3} $ 使得 $ \overrightarrow {AC}={\lambda }_{3}\overrightarrow {AD} $ ,故 $ \mathrm{B} $ , $ \mathrm{C} $ 错误;
由于 $ \overrightarrow {BC}=\overrightarrow {AC}-\overrightarrow {AB}=4\boldsymbol{a}-4\boldsymbol{b}-(\boldsymbol{a}+2\boldsymbol{b})=3\boldsymbol{a}-6\boldsymbol{b} $ ,
所以 $ \overrightarrow {BC}=-3\overrightarrow {CD} $ ,又 $ \overrightarrow {BC} $ , $ \overrightarrow {CD} $ 有共同的端点 $ C $ ,所以 $ B $ , $ C $ , $ D $ 三点共线,故 $ \mathrm{D} $ 正确.
7.已知向量 $ \boldsymbol{a}=2{\boldsymbol{e}}_{1}-3{\boldsymbol{e}}_{2} $ , $ \boldsymbol{b}=2{\boldsymbol{e}}_{1}+3{\boldsymbol{e}}_{2} $ , $ \boldsymbol{c}=2{\boldsymbol{e}}_{1}-9{\boldsymbol{e}}_{2} $ ,其中 $ {\boldsymbol{e}}_{1} $ , $ {\boldsymbol{e}}_{2} $ 不共线.问是否存在实数 $ \lambda $ , $ \mu $ ,使向量 $ \boldsymbol{d}=\lambda \boldsymbol{a}+\mu \boldsymbol{b} $ 与 $ \boldsymbol{c} $ 共线?
答案:【解】由题意得 $ \boldsymbol{d}=\lambda \boldsymbol{a}+\mu \boldsymbol{b}=(2\lambda +2\mu ){\boldsymbol{e}}_{1}+(-3\lambda +3\mu ){\boldsymbol{e}}_{2} $ ,
若 $ \boldsymbol{d} $ 与 $ \boldsymbol{c} $ 共线,则存在实数 $ k\ne 0 $ ,使 $ \boldsymbol{d}=k\boldsymbol{c} $ ,
即 $ (2\lambda +2\mu ){\boldsymbol{e}}_{1}+(-3\lambda +3\mu ){\boldsymbol{e}}_{2}=2k{\boldsymbol{e}}_{1}-9k{\boldsymbol{e}}_{2} $ ,
即 $ (2\lambda +2\mu ){\boldsymbol{e}}_{1}-2k{\boldsymbol{e}}_{1}=-9k{\boldsymbol{e}}_{2}-(-3\lambda +3\mu )\cdot {\boldsymbol{e}}_{2} $ ,即 $ \begin{cases}2\lambda +2\mu -2k=0,\\ -9k+3\lambda -3\mu =0,\end{cases} $
解得 $ \lambda =-2\mu $ .
故存在实数 $ \lambda $ , $ \mu $ ,且 $ \lambda =-2\mu $ ,使 $ \boldsymbol{d} $ 与 $ \boldsymbol{c} $ 共线.
解析:
8.已知向量 $ {\boldsymbol{e}}_{1} $ , $ {\boldsymbol{e}}_{2} $ 不共线, $ \boldsymbol{a}=2{\boldsymbol{e}}_{1}+t{\boldsymbol{e}}_{2} $ , $ \boldsymbol{b}=(t+3)\cdot {\boldsymbol{e}}_{1}+2{\boldsymbol{e}}_{2} $ ,且 $ \boldsymbol{a}//\boldsymbol{b} $ ,则实数 $ t= $ ( )
A.1或4
B.1或 $ -4 $
C. $ \dfrac{1}{4} $ 或1
D. $ -\dfrac{1}{4} $ 或1
答案:B
解析:因为 $ \boldsymbol{a}=2{\boldsymbol{e}}_{1}+t{\boldsymbol{e}}_{2} $ , $ \boldsymbol{b}=(t+3){\boldsymbol{e}}_{1}+2{\boldsymbol{e}}_{2} $ ,且 $ \boldsymbol{a}//\boldsymbol{b} $ ,
所以 $ 2{\boldsymbol{e}}_{1}+t{\boldsymbol{e}}_{2}=\lambda [(t+3){\boldsymbol{e}}_{1}+2{\boldsymbol{e}}_{2}]=\lambda (t+3)\cdot {\boldsymbol{e}}_{1}+2\lambda {\boldsymbol{e}}_{2}(\lambda \in \boldsymbol{R}) $ ,即 $ [2-\lambda (t+3)]{\boldsymbol{e}}_{1}=(2\lambda -t){\boldsymbol{e}}_{2} $ ,
又向量 $ {e}_{1} $ , $ {e}_{2} $ 不共线,可得 $ \begin{cases}2=\lambda (t+3),\\ t=2\lambda ,\end{cases} $
消去 $ \lambda $ 得到 $ {t}^{2}+3t-4=0 $ ,解得 $ t=1 $ 或 $ t=-4 $ ,
故选 $ \mathrm{B} $ .
9.设 $ \boldsymbol{a} $ 与 $ \boldsymbol{b} $ 都是非零向量.下列四个条件中,使 $ \dfrac{\boldsymbol{a}}{|\boldsymbol{a}|}=\dfrac{\boldsymbol{b}}{|\boldsymbol{b}|} $ 成立的充分条件是( )
A. $ |\boldsymbol{a}|=|\boldsymbol{b}| $ 且 $ \boldsymbol{a}//\boldsymbol{b} $
B. $ \boldsymbol{a}=-\boldsymbol{b} $
C. $ \boldsymbol{a}=2\boldsymbol{b} $
D. $ \boldsymbol{a}//\boldsymbol{b} $
答案:C
解析:对于 $ \mathrm{A} $ ,向量 $ \boldsymbol{a} $ 与 $ \boldsymbol{b} $ 满足 $ |\boldsymbol{a}|=|\boldsymbol{b}| $ 且 $ \boldsymbol{a}//\boldsymbol{b} $ ,若向量 $ \boldsymbol{a} $ 与 $ \boldsymbol{b} $ 反向,则 $ \dfrac{\boldsymbol{a}}{|\boldsymbol{a}|}=-\dfrac{\boldsymbol{b}}{|\boldsymbol{b}|} $ ,故 $ \mathrm{A} $ 不符合题意;
对于 $ \mathrm{B} $ ,由 $ \boldsymbol{a}=-\boldsymbol{b} $ ,则 $ \dfrac{\boldsymbol{a}}{|\boldsymbol{a}|}=-\dfrac{\boldsymbol{b}}{|\boldsymbol{b}|} $ ,故 $ \mathrm{B} $ 不符合题意;对于 $ \mathrm{C} $ ,因为 $ \boldsymbol{a}=2\boldsymbol{b} $ ,所以向量 $ \boldsymbol{a} $ 与 $ \boldsymbol{b} $ 同向,所以 $ \dfrac{\boldsymbol{a}}{|\boldsymbol{a}|}=\dfrac{\boldsymbol{b}}{|\boldsymbol{b}|} $ ,故 $ \mathrm{C} $ 符合题意;
对于 $ \mathrm{D} $ ,向量 $ \boldsymbol{a} $ 与 $ \boldsymbol{b} $ 满足 $ \boldsymbol{a}//\boldsymbol{b} $ ,若向量 $ \boldsymbol{a} $ 与 $ \boldsymbol{b} $ 反向,则 $ \dfrac{\boldsymbol{a}}{|\boldsymbol{a}|}=-\dfrac{\boldsymbol{b}}{|\boldsymbol{b}|} $ ,故 $ \mathrm{D} $ 不符合题意.故选 $ \mathrm{C} $ .
10.设 $ \boldsymbol{a} $ , $ \boldsymbol{b} $ 是两个不共线的向量,若 $ \overrightarrow {AB}=2\boldsymbol{a}+k\boldsymbol{b} $ , $ \overrightarrow {BC}=\boldsymbol{a}+3\boldsymbol{b} $ , $ \overrightarrow {CD}=2\boldsymbol{a}-\boldsymbol{b} $ ,且 $ A $ , $ B $ , $ D $ 三点共线,则实数 $ k $ 的值为 .
解析:由 $ \overrightarrow {BC}=\boldsymbol{a}+3\boldsymbol{b} $ , $ \overrightarrow {CD}=2\boldsymbol{a}-\boldsymbol{b} $ ,得 $ \overrightarrow {BD}=\overrightarrow {BC}+\overrightarrow {CD}=(\boldsymbol{a}+3\boldsymbol{b})+(2\boldsymbol{a}-\boldsymbol{b})=3\boldsymbol{a}+2\boldsymbol{b} $ ,
由 $ A $ , $ B $ , $ D $ 三点共线,得 $ \overrightarrow {AB}//\overrightarrow {BD} $ ,而 $ \overrightarrow {AB}=2\boldsymbol{a}+k\boldsymbol{b} $ ,
则 $ 2\boldsymbol{a}+k\boldsymbol{b}=t(3\boldsymbol{a}+2\boldsymbol{b}) $ ,又 $ \boldsymbol{a} $ , $ \boldsymbol{b} $ 不共线,因此 $ \begin{cases}2=3t,\\ k=2t,\end{cases} $ 解得 $ k=\dfrac{4}{3} $ ,所以实数 $ k $ 的值为 $ \dfrac{4}{3} $ .
二、刷提升
1.如图,在 $ △OCB $ 中, $ A $ 是边 $ BC $ 的中点, $ D $ 是边 $ OB $ 上靠近点 $ O $ 的三等分点,设 $ \overrightarrow {OA}=\boldsymbol{a} $ , $ \overrightarrow {OB}=\boldsymbol{b} $ ,则 $ \overrightarrow {DC}= $ ( )
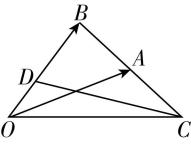
A. $ 2\boldsymbol{a}-\dfrac{5}{3}\boldsymbol{b} $
B. $ 2\boldsymbol{a}+\dfrac{5}{3}\boldsymbol{b} $
C. $ 2\boldsymbol{a}-\dfrac{4}{3}\boldsymbol{b} $
D. $ -2\boldsymbol{a}+\dfrac{4}{3}\boldsymbol{b} $
答案:C
解析: $ \because A $ 是边 $ BC $ 的中点, $ \therefore \overrightarrow {AC}=\overrightarrow {BA} $ ,
$ \therefore \overrightarrow {OC}=\overrightarrow {OA}+\overrightarrow {AC}=\overrightarrow {OA}+\overrightarrow {BA}=\overrightarrow {OA}+(\overrightarrow {OA}-\overrightarrow {OB})=2\overrightarrow {OA}-\overrightarrow {OB} $ ,
$ \because D $ 是边 $ OB $ 上靠近点 $ O $ 的三等分点, $ \therefore \overrightarrow {DO}=-\dfrac{1}{3}\overrightarrow {OB} $ ,
$ \therefore \overrightarrow {DC}=\overrightarrow {DO}+\overrightarrow {OC}=-\dfrac{1}{3}\overrightarrow {OB}+(2\overrightarrow {OA}-\overrightarrow {OB})=2\overrightarrow {OA}-\dfrac{4}{3}\overrightarrow {OB} $ ,
又 $ \overrightarrow {OA}=\boldsymbol{a} $ , $ \overrightarrow {OB}=\boldsymbol{b} $ , $ \therefore \overrightarrow {DC}=2\boldsymbol{a}-\dfrac{4}{3}\boldsymbol{b} $ .
故选 $ \mathrm{C} $ .
2.在等腰梯形 $ ABCD $ 中,下列结论一定正确的是( )
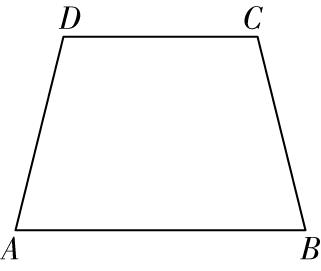
A. $ \overrightarrow {DA}=\overrightarrow {CB} $
B. $ \overrightarrow {AD}+\overrightarrow {AB}=\overrightarrow {AC} $
C. $ \overrightarrow {AD}+\dfrac{1}{2}\overrightarrow {AB}=\overrightarrow {AC} $
D. $ |\overrightarrow {DA}+\overrightarrow {DB}|=|\overrightarrow {CA}+\overrightarrow {CB}| $
答案:D
解析:对于 $ \mathrm{A} $ ,因为向量 $ \overrightarrow {DA} $ , $ \overrightarrow {CB} $ 的方向不相同,所以向量 $ \overrightarrow {DA} $ , $ \overrightarrow {CB} $ 不相等, $ \mathrm{A} $ 错误;
对于 $ \mathrm{B} $ ,如图①,以 $ AB $ , $ AD $ 为邻边作平行四边形 $ ABED $ ,可得 $ \overrightarrow {AD}+\overrightarrow {AB}=\overrightarrow {AE} $ ,所以 $ \overrightarrow {AD}+\overrightarrow {AB}\ne \overrightarrow {AC} $ , $ \mathrm{B} $ 错误;

图①
对于 $ \mathrm{C} $ ,记 $ AB $ 的中点为 $ F $ ,则 $ \overrightarrow {AF}=\dfrac{1}{2}\overrightarrow {AB} $ ,以 $ AF $ , $ AD $ 为邻边作平行四边形 $ AFGD $ ,如图②,所以 $ \overrightarrow {AD}+\dfrac{1}{2}\overrightarrow {AB}=\overrightarrow {AD}+\overrightarrow {AF}=\overrightarrow {AG} $ ,点 $ G $ 与点 $ C $ 不一定重合,所以 $ \mathrm{C} $ 错误;
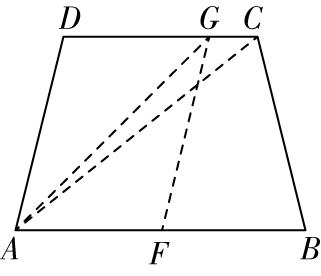
图②
对于 $ \mathrm{D} $ ,记 $ AB $ 的中点为 $ F $ ,由向量运算可得 $ \overrightarrow {DA}+\overrightarrow {DB}=2\overrightarrow {DF} $ , $ \overrightarrow {CA}+\overrightarrow {CB}=2\overrightarrow {CF} $ ,所以 $ |\overrightarrow {DA}+\overrightarrow {DB}|=2|\overrightarrow {DF}| $ , $ |\overrightarrow {CA}+\overrightarrow {CB}|=2|\overrightarrow {CF}| $ .
由已知得 $ AD=BC $ , $ AF=BF $ , $ \mathrm{\angle }DAB=\mathrm{\angle }CBA $ ,所以 $ △DAF≌△CBF $ ,所以 $ DF=CF $ ,即 $ |\overrightarrow {DF}|=|\overrightarrow {CF}| $ ,所以 $ |\overrightarrow {DA}+\overrightarrow {DB}|=|\overrightarrow {CA}+\overrightarrow {CB}| $ , $ \mathrm{D} $ 正确.故选 $ \mathrm{D} $ .
3.已知向量 $ \boldsymbol{a} $ , $ \boldsymbol{b} $ 不共线,且 $ \boldsymbol{c}=\lambda \boldsymbol{a}+\boldsymbol{b} $ , $ \boldsymbol{d}=\boldsymbol{a}+(2\lambda -1)\boldsymbol{b} $ ,若 $ \boldsymbol{c} $ 与 $ \boldsymbol{d} $ 反向共线,则实数 $ \lambda $ 的值为( )
A.1
B. $ -\dfrac{1}{2} $
C. $ \dfrac{1}{2} $
D. $ -2 $
答案:B
解析: $ \boldsymbol{c} $ 与 $ \boldsymbol{d} $ 反向共线,则存在实数 $ k $ 使 $ \boldsymbol{c}=k\boldsymbol{d}(k < 0) $ ,
于是 $ \lambda \boldsymbol{a}+\boldsymbol{b}=k\boldsymbol{a}+k(2\lambda -1)\boldsymbol{b}=k\boldsymbol{a}+(2\lambda k-k)\boldsymbol{b} $ ,因为 $ \boldsymbol{a} $ , $ \boldsymbol{b} $ 不共线,所以 $ \begin{cases}\lambda =k,\\ 2\lambda k-k=1,\end{cases} $ 整理得 $ 2{\lambda }^{2}-\lambda -1=0 $ ,解得 $ \lambda =1 $ 或 $ \lambda =-\dfrac{1}{2} $ .
又因为 $ k < 0 $ ,所以 $ \lambda < 0 $ ,故 $ \lambda =-\dfrac{1}{2} $ .故选 $ \mathrm{B} $ .
4.在 $ △ABC $ 中,若 $ \overrightarrow {OQ}=\overrightarrow {OA}+\lambda (\dfrac{\overrightarrow {AB}}{|\overrightarrow {AB}|}+\dfrac{\overrightarrow {AC}}{|\overrightarrow {AC}|}) $ , $ \lambda \in [0,+\mathrm{\infty }) $ ,则点 $ Q $ 的轨迹必经过 $ △ABC $ 的( )
A.内心
B.外心
C.重心
D.垂心
答案:A
解析:因为 $ \dfrac{\overrightarrow {AB}}{|\overrightarrow {AB}|} $ 是与 $ \overrightarrow {AB} $ 同向的单位向量, $ \dfrac{\overrightarrow {AC}}{|\overrightarrow {AC}|} $ 是与 $ \overrightarrow {AC} $ 同向的单位向量,

如图,设 $ \overrightarrow {AN}=\dfrac{\overrightarrow {AB}}{|\overrightarrow {AB}|} $ , $ \overrightarrow {AM}=\dfrac{\overrightarrow {AC}}{|\overrightarrow {AC}|} $ ,
则 $ \overrightarrow {OQ}=\overrightarrow {OA}+\lambda (\dfrac{\overrightarrow {AB}}{|\overrightarrow {AB}|}+\dfrac{\overrightarrow {AC}}{|\overrightarrow {AC}|}) $ 可化为 $ \overrightarrow {AQ}=\lambda (\overrightarrow {AN}+\overrightarrow {AM}) $ ,且 $ AM=AN $ ,
以 $ AM $ , $ AN $ 为邻边作平行四边形 $ AMEN $ ,
则 $ \overrightarrow {AE}=\overrightarrow {AM}+\overrightarrow {AN} $ ,且平行四边形 $ AMEN $ 为菱形,所以 $ AE $ 平分 $ \mathrm{\angle }MAN $ ,
所以 $ \overrightarrow {AQ}=\lambda \overrightarrow {AE} $ ,又 $ \overrightarrow {AQ} $ 与 $ \overrightarrow {AE} $ 有公共端点 $ A $ ,所以 $ A $ , $ E $ , $ Q $ 三点共线,所以 $ \overrightarrow {AQ} $ 在 $ \mathrm{\angle }BAC $ 的平分线上,则点 $ Q $ 的轨迹必经过 $ △ABC $ 的内心,故选 $ \mathrm{A} $ .
5.点 $ O $ 在 $ △ABC $ 的内部,且满足 $ \overrightarrow {AO}=\dfrac{1}{5}\overrightarrow {AB}+\dfrac{2}{5}\overrightarrow {AC} $ ,则 $ △ABC $ 的面积与 $ △AOB $ 的面积之比是( )
A. $ \dfrac{7}{2} $
B.3
C. $ \dfrac{5}{2} $
D.2
答案:C
解析:因为 $ \overrightarrow {AO}=\dfrac{1}{5}\overrightarrow {AB}+\dfrac{2}{5}\overrightarrow {AC} $ ,
所以 $ \overrightarrow {AO}=\dfrac{1}{5}(\overrightarrow {OB}-\overrightarrow {OA})+\dfrac{2}{5}(\overrightarrow {OC}-\overrightarrow {OA}) $ ,即 $ \overrightarrow {OB}+2\overrightarrow {OA}+2\overrightarrow {OC}=0 $ ,取 $ AC $ 的中点为点 $ D $ ,如图,
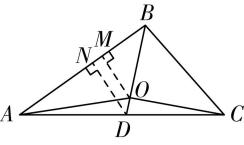
则 $ \overrightarrow {OA}+\overrightarrow {OC}=2\overrightarrow {OD} $ ,即 $ 4\overrightarrow {OD}=-\overrightarrow {OB} $ ,
所以点 $ O $ 在 $ △ABC $ 的中线 $ BD $ 上,且 $ OB=\dfrac{4}{5}BD $ .
过点 $ O $ , $ D $ 分别作边 $ AB $ 上的垂线,垂足分别为 $ M $ , $ N $ ,
则 $ \dfrac{OM}{DN}=\dfrac{OB}{BD}=\dfrac{4}{5} $ ,
所以 $ {S}_{△AOB}=\dfrac{4}{5}{S}_{△ABD} $ ,又 $ {S}_{△ABD}=\dfrac{1}{2}{S}_{△ABC} $ ,
所以 $ {S}_{△AOB}=\dfrac{2}{5}{S}_{△ABC} $ ,所以 $ \dfrac{{S}_{△ABC}}{{S}_{△AOB}}=\dfrac{5}{2} $ ,故选 $ \mathrm{C} $ .
6.(多选)在 $ △ABC $ 中, $ \overrightarrow {CD}=\dfrac{2}{3}\overrightarrow {CA} $ , $ P $ 为线段 $ BD $ 上一点,且有 $ \overrightarrow {AP}=\lambda \overrightarrow {AB}+\mu \overrightarrow {AC} $ , $ \lambda $ , $ \mu \in (0,+\mathrm{\infty }) $ ,则下列结论正确的是( )(多选)
A. $ \lambda +\mu =1 $
B. $ \lambda +3\mu =1 $
C. $ \lambda \mu $ 的最大值为 $ \dfrac{1}{12} $
D. $ \dfrac{1}{\lambda }+\dfrac{1}{\mu } $ 的最小值为 $ 4+2\sqrt{3} $
答案:BCD
解析:如图,因为 $ \overrightarrow {CD}=\dfrac{2}{3}\overrightarrow {CA} $ , $ P $ 为线段 $ BD $ 上一点,
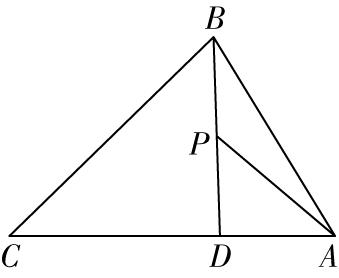
所以 $ \overrightarrow {AP}=\lambda \overrightarrow {AB}+\mu \overrightarrow {AC}=\lambda \overrightarrow {AB}+3\mu \overrightarrow {AD} $ ,
而点 $ P $ 在线段 $ BD $ 上,所以 $ \lambda +3\mu =1 $ , $ \lambda \in (0,1) $ , $ 3\mu \in (0,1) $ , $ \mathrm{A} $ 错误, $ \mathrm{B} $ 正确;
由基本不等式可得 $ \lambda +3\mu =1\geqslant 2\sqrt{3\lambda \mu } $ ,解得 $ \lambda \mu \leqslant \dfrac{1}{12} $ ,当且仅当 $ \lambda =\dfrac{1}{2} $ , $ \mu =\dfrac{1}{6} $ 时等号成立, $ \mathrm{C} $ 正确;
$ \dfrac{1}{\lambda }+\dfrac{1}{\mu }=(\dfrac{1}{\lambda }+\dfrac{1}{\mu })(\lambda +3\mu )=4+\dfrac{3\mu }{\lambda }+\dfrac{\lambda }{\mu }\geqslant 4+2\sqrt{3} $ ,当且仅当 $ \mu =\dfrac{3-\sqrt{3}}{6} $ , $ \lambda =\dfrac{\sqrt{3}-1}{2} $ 时等号成立, $ \mathrm{D} $ 正确.
故选 $ \mathrm{B}\mathrm{C}\mathrm{D} $ .
7.设 $ {\boldsymbol{e}}_{1} $ , $ {\boldsymbol{e}}_{2} $ 是两个不共线的向量,已知 $ \overrightarrow {AB}=2{\boldsymbol{e}}_{1}-6{\boldsymbol{e}}_{2} $ , $ \overrightarrow {CB}={\boldsymbol{e}}_{1}+2{\boldsymbol{e}}_{2} $ , $ \overrightarrow {CD}=2{\boldsymbol{e}}_{1}-{\boldsymbol{e}}_{2} $ .
(1) 求证: $ A $ , $ B $ , $ D $ 三点共线;
(2) 若 $ \overrightarrow {BF}=3{\boldsymbol{e}}_{1}-k{\boldsymbol{e}}_{2} $ ,且 $ \overrightarrow {BF}//\overrightarrow {BD} $ ,求实数 $ k $ 的值.
答案:(1) 【证明】因为 $ \overrightarrow {AB}=2{\boldsymbol{e}}_{1}-6{\boldsymbol{e}}_{2} $ , $ \overrightarrow {CB}={\boldsymbol{e}}_{1}+2{\boldsymbol{e}}_{2} $ , $ \overrightarrow {CD}=2{\boldsymbol{e}}_{1}-{\boldsymbol{e}}_{2} $ ,
所以 $ \overrightarrow {BD}=\overrightarrow {CD}-\overrightarrow {CB}=2{\boldsymbol{e}}_{1}-{\boldsymbol{e}}_{2}-({\boldsymbol{e}}_{1}+2{\boldsymbol{e}}_{2})={\boldsymbol{e}}_{1}-3{\boldsymbol{e}}_{2} $ ,
所以 $ \overrightarrow {AB}=2\overrightarrow {BD} $ ,
所以 $ \overrightarrow {AB} $ , $ \overrightarrow {BD} $ 共线,又 $ \overrightarrow {AB} $ 与 $ \overrightarrow {BD} $ 有公共点 $ B $ ,
所以 $ A $ , $ B $ , $ D $ 三点共线.
(2) 【解】因为 $ \overrightarrow {BF}=3{\boldsymbol{e}}_{1}-k{\boldsymbol{e}}_{2} $ ,且 $ \overrightarrow {BF}//\overrightarrow {BD} $ ,
所以 $ \overrightarrow {BF}=\lambda \overrightarrow {BD} $ ,
即 $ 3{\boldsymbol{e}}_{1}-k{\boldsymbol{e}}_{2}=\lambda ({\boldsymbol{e}}_{1}-3{\boldsymbol{e}}_{2}) $ ,
所以 $ \begin{cases}3=\lambda ,\\ -k=-3\lambda ,\end{cases} $ 所以 $ \begin{cases}\lambda =3,\\ k=9,\end{cases} $
所以实数 $ k $ 的值为9.
解析:
8.已知向量 $ \boldsymbol{a} $ , $ \boldsymbol{b} $ 不共线,若向量 $ \boldsymbol{a}+\lambda \boldsymbol{b} $ 与 $ \boldsymbol{b}+\lambda \boldsymbol{a} $ 的方向相反,则 $ \lambda $ 的值为( )
A.1
B.0
C. $ -1 $
D. $ ±1 $
答案:C
解析: $ \because $ 向量 $ \boldsymbol{a}+\lambda \boldsymbol{b} $ 与 $ \boldsymbol{b}+\lambda \boldsymbol{a} $ 的方向相反, $ \therefore (\boldsymbol{a}+\lambda \boldsymbol{b})//(\boldsymbol{b}+\lambda \boldsymbol{a}) $ .由向量共线的充要条件可知,存在一个实数 $ m $ ,使得 $ \boldsymbol{a}+\lambda \boldsymbol{b}=m(\boldsymbol{b}+\lambda \boldsymbol{a}) $ ,即 $ (1-m\lambda )\boldsymbol{a}=(m-\lambda )\boldsymbol{b} $ . $ \because \boldsymbol{a} $ 与 $ \boldsymbol{b} $ 不共线, $ \therefore 1-m\lambda =m-\lambda =0 $ ,可得 $ m=\lambda .\therefore 1-{\lambda }^{2}=0 $ , $ \lambda =±1. $ 当 $ \lambda =1 $ 时,向量 $ \boldsymbol{a}+\boldsymbol{b} $ 与 $ \boldsymbol{b}+\boldsymbol{a} $ 是相等向量,其方向相同,不符合题意,故舍去 $ {\rm .} \therefore \lambda =-1 $ .
9.已知向量 $ \boldsymbol{a} $ , $ \boldsymbol{b} $ 满足 $ |2\boldsymbol{a}-\boldsymbol{b}|=|\boldsymbol{a}+2\boldsymbol{b}|=1 $ ,则 $ |3\boldsymbol{a}+4\boldsymbol{b}| $ 的最大值为 .
解析:设 $ 3\boldsymbol{a}+4\boldsymbol{b}=x(2\boldsymbol{a}-\boldsymbol{b})+y(\boldsymbol{a}+2\boldsymbol{b}) $ ,可得 $ \begin{cases}2x+y=3,\\ -x+2y=4,\end{cases} $ 解得 $ \begin{cases}x=\dfrac{2}{5},\\ y=\dfrac{11}{5},\end{cases} $ 即 $ 3\boldsymbol{a}+4\boldsymbol{b}=\dfrac{2}{5}(2\boldsymbol{a}-\boldsymbol{b})+\dfrac{11}{5}(\boldsymbol{a}+2\boldsymbol{b}) $ ,
由向量三角不等式可知 $ |3\boldsymbol{a}+4\boldsymbol{b}|\leqslant \dfrac{2}{5}|2\boldsymbol{a}-\boldsymbol{b}|+\dfrac{11}{5}|\boldsymbol{a}+2\boldsymbol{b}|=\dfrac{2}{5}+\dfrac{11}{5}=\dfrac{13}{5} $ ,当且仅当 $ 2\boldsymbol{a}-\boldsymbol{b} $ , $ \boldsymbol{a}+2\boldsymbol{b} $ 同向共线时,等号成立,因此 $ |3\boldsymbol{a}+4\boldsymbol{b}| $ 的最大值为 $ \dfrac{13}{5} $ .







