6.2.4 向量的数量积
一、刷基础
1.已知边长为2的正方形 $ ABCD $ 中,点 $ E $ , $ F $ 分别为 $ AB $ , $ BC $ 的中点,则 $ \overrightarrow {AF}\cdot \overrightarrow {AE}= $ ( )
A.1
B.2
C.3
D.4
答案:B
解析:因为点 $ E $ , $ F $ 分别为 $ AB $ , $ BC $ 的中点,

所以 $ |\overrightarrow {AE}|=\dfrac{1}{2}|\overrightarrow {AB}|=1 $ , $ |\overrightarrow {AF}|=\sqrt{A{B}^{2}+B{F}^{2}}=\sqrt{5} $ , $ \cos \mathrm{\angle }FAB=\dfrac{2}{\sqrt{5}} $ ,则 $ \overrightarrow {AF}\cdot \overrightarrow {AE}=\sqrt{5}×1×\dfrac{2}{\sqrt{5}}=2 $ .故选 $ \mathrm{B} $ .
2.下列说法不正确的有( )(多选)
A. $ \boldsymbol{a}\cdot \boldsymbol{b}=0⇒\boldsymbol{a}=0 $ 或 $ \boldsymbol{b}=0 $
B. $ (\boldsymbol{a}\cdot \boldsymbol{b})\boldsymbol{c}=\boldsymbol{a}(\boldsymbol{b}\cdot \boldsymbol{c}) $
C.已知 $ \boldsymbol{a} $ , $ \boldsymbol{b} $ 为非零向量,且 $ |\boldsymbol{a}+\boldsymbol{b}|=|\boldsymbol{a}|+|\boldsymbol{b}| $ ,则 $ \boldsymbol{a} $ 与 $ \boldsymbol{b} $ 方向相同
D.若 $ \boldsymbol{a}\cdot \boldsymbol{b} < 0 $ ,则 $ \boldsymbol{a} $ 与 $ \boldsymbol{b} $ 的夹角是钝角
答案:ABD
解析:对于 $ \mathrm{A} $ ,由 $ \boldsymbol{a}\cdot \boldsymbol{b}=0 $ 可得 $ \boldsymbol{a}\perp \boldsymbol{b} $ ,故 $ \mathrm{A} $ 错误;
对于 $ \mathrm{B} $ ,向量的数量积不满足结合律,故 $ \mathrm{B} $ 错误;
对于 $ \mathrm{C} $ ,由 $ \boldsymbol{a} $ , $ \boldsymbol{b} $ 为非零向量,且 $ |\boldsymbol{a}+\boldsymbol{b}|=|\boldsymbol{a}|+|\boldsymbol{b}| $ ,则 $ \boldsymbol{a} $ 与 $ \boldsymbol{b} $ 方向相同,故 $ \mathrm{C} $ 正确;
对于 $ \mathrm{D} $ ,当 $ \boldsymbol{a} $ , $ \boldsymbol{b} $ 反向时,有 $ \boldsymbol{a}\cdot \boldsymbol{b} < 0 $ ,此时 $ \boldsymbol{a} $ 与 $ \boldsymbol{b} $ 的夹角不是钝角,故 $ \mathrm{D} $ 错误.
故选 $ \mathrm{A}\mathrm{B}\mathrm{D} $ .
3.已知向量 $ |\boldsymbol{a}|=2 $ , $ \boldsymbol{b} $ 在 $ \boldsymbol{a} $ 上的投影向量为 $ -2\boldsymbol{a} $ ,则 $ \boldsymbol{a}\cdot \boldsymbol{b}= $ ( )
A. $ -8 $
B.8
C.4
D. $ -4 $
答案:A
解析:根据数量积的几何意义, $ \boldsymbol{a}\cdot \boldsymbol{b} $ 等于 $ \boldsymbol{a} $ 与 $ \boldsymbol{b} $ 在 $ \boldsymbol{a} $ 上的投影向量的数量积,故 $ \boldsymbol{a}\cdot \boldsymbol{b}=\boldsymbol{a}\cdot (-2\boldsymbol{a})=-8 $ .故选 $ \mathrm{A} $ .
4.已知 $ △ABC $ 外接圆的圆心为 $ O $ ,半径为 $ {\rm 2,} \overrightarrow {OA}+\overrightarrow {AB}+\overrightarrow {AC}=0 $ 且 $ |\overrightarrow {OA}|=|\overrightarrow {AB}| $ ,则向量 $ \overrightarrow {CA} $ 在 $ \overrightarrow {CB} $ 上的投影向量的模为 .
解析:如图,因为 $ \overrightarrow {OA}+\overrightarrow {AB}+\overrightarrow {AC}=0 $ ,所以 $ \overrightarrow {OB}+\overrightarrow {AC}=0 $ ,
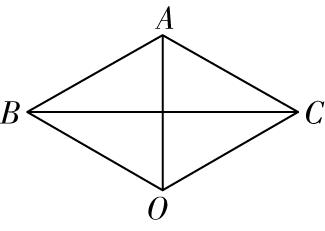
所以 $ \overrightarrow {OB}=\overrightarrow {CA} $ ,则四边形 $ ABOC $ 为平行四边形.
又 $ O $ 为 $ △ABC $ 外接圆的圆心,且 $ |\overrightarrow {AB}|=|\overrightarrow {OA}|=2 $ ,
所以 $ △OAB $ 是边长为2的正三角形,
所以平行四边形 $ ABOC $ 是边长为2的菱形且 $ \mathrm{\angle }ABO={60}^{\circ } $ ,
所以 $ |\overrightarrow {CA}|=2 $ , $ \mathrm{\angle }ACB={30}^{\circ } $ ,
故向量 $ \overrightarrow {CA} $ 在 $ \overrightarrow {CB} $ 上的投影向量的模为 $ |\overrightarrow {CA}| \cos \mathrm{\angle }ACB=2 \cos {30}^{\circ }=\sqrt{3} $ .
5.已知向量 $ \boldsymbol{a} $ , $ \boldsymbol{b} $ 满足 $ |\boldsymbol{a}|=2|\boldsymbol{b}|=2 $ , $ |\boldsymbol{a}+\boldsymbol{b}|=\sqrt{7} $ ,则 $ \boldsymbol{a} $ 与 $ \boldsymbol{b} $ 的夹角为( )
A. $ {90}^{\circ } $
B. $ {60}^{\circ } $
C. $ {45}^{\circ } $
D. $ {30}^{\circ } $
答案:B
解析:由 $ |\boldsymbol{a}+\boldsymbol{b}|=\sqrt{7} $ ,得 $ (\boldsymbol{a}+\boldsymbol{b})^{2}=7 $ ,即 $ {\boldsymbol{a}}^{2}+2\boldsymbol{a}\cdot \boldsymbol{b}+{\boldsymbol{b}}^{2}=7 $ ,则 $ |\boldsymbol{a}{|}^{2}+2|\boldsymbol{a}|\cdot |\boldsymbol{b}| \cos ⟨\boldsymbol{a} $ , $ \boldsymbol{b}⟩+{|\boldsymbol{b}|}^{2}=7 $ ,又 $ |\boldsymbol{a}|=2|\boldsymbol{b}|=2 $ ,所以 $ \cos ⟨\boldsymbol{a} $ , $ \boldsymbol{b}⟩=\dfrac{1}{2} $ ,又 $ {0}^{\circ }\leqslant ⟨\boldsymbol{a} $ , $ \boldsymbol{b}⟩\leqslant {180}^{\circ } $ ,所以 $ \boldsymbol{a} $ 与 $ \boldsymbol{b} $ 的夹角为 $ {60}^{\circ } $ .故选 $ \mathrm{B} $ .
6.已知向量 $ \boldsymbol{a} $ , $ \boldsymbol{b} $ , $ \boldsymbol{c} $ 满足:| $ \boldsymbol{a}|=|\boldsymbol{b}|=1 $ , $ |\boldsymbol{c}|=\dfrac{\sqrt{3}}{2} $ ,且 $ \boldsymbol{a}+\boldsymbol{b}=2\boldsymbol{c} $ ,则 $ \boldsymbol{a} $ 与 $ \boldsymbol{c} $ 的夹角为( )
A. $ \dfrac{\mathrm{\pi }}{6} $
B. $ \dfrac{\mathrm{\pi }}{3} $
C. $ \dfrac{2\mathrm{\pi }}{3} $
D. $ \dfrac{5\mathrm{\pi }}{6} $
答案:A
解析:由 $ \boldsymbol{a}+\boldsymbol{b}=2\boldsymbol{c} $ 两边平方可得 $ {\boldsymbol{a}}^{2}+2\boldsymbol{a}\cdot \boldsymbol{b}+{\boldsymbol{b}}^{2}=4{\boldsymbol{c}}^{2} $ ,又 $ |\boldsymbol{a}|=|\boldsymbol{b}|=1 $ , $ |\boldsymbol{c}|=\dfrac{\sqrt{3}}{2} $ ,所以 $ 1+2\boldsymbol{a}\cdot \boldsymbol{b}+1=3⇒\boldsymbol{a}\cdot \boldsymbol{b}=\dfrac{1}{2} $ ,所以 $ \cos ⟨\boldsymbol{a} $ , $ \boldsymbol{c}⟩=\dfrac{\boldsymbol{a}\cdot \dfrac{1}{2}(\boldsymbol{a}+\boldsymbol{b})}{\dfrac{\sqrt{3}}{2}}=\dfrac{{\boldsymbol{a}}^{2}+\boldsymbol{a}\cdot \boldsymbol{b}}{\sqrt{3}}=\dfrac{1+\dfrac{1}{2}}{\sqrt{3}}=\dfrac{\sqrt{3}}{2} $ .因为 $ ⟨\boldsymbol{a} $ , $ \boldsymbol{c}⟩\in [0,\mathrm{\pi }] $ ,所以 $ ⟨\boldsymbol{a} $ , $ \boldsymbol{c}⟩=\dfrac{\mathrm{\pi }}{6} $ .故选 $ \mathrm{A} $ .
7.已知向量 $ \boldsymbol{a} $ , $ \boldsymbol{b} $ 满足 $ |\boldsymbol{a}-\boldsymbol{b}|=\sqrt{6} $ , $ |\boldsymbol{a}+\boldsymbol{b}|=|2\boldsymbol{a}-\boldsymbol{b}| $ ,则 $ |\boldsymbol{b}| $ 为( )
A. $ \sqrt{2} $
B. $ \sqrt{3} $
C. $ \sqrt{5} $
D. $ \sqrt{6} $
答案:D
解析:因为 $ |\boldsymbol{a}+\boldsymbol{b}|=|2\boldsymbol{a}-\boldsymbol{b}| $ ,即 $ (\boldsymbol{a}+\boldsymbol{b})^{2}={\left(2\boldsymbol{a}-\boldsymbol{b} \right) ^ {2}} $ ,则 $ {\boldsymbol{a}}^{2}+2\boldsymbol{a}\cdot \boldsymbol{b}+{\boldsymbol{b}}^{2}=4{\boldsymbol{a}}^{2}-4\boldsymbol{a}\cdot \boldsymbol{b}+{\boldsymbol{b}}^{2} $ ,整理得 $ {\boldsymbol{a}}^{2}-2\boldsymbol{a}\cdot \boldsymbol{b}=0 $ ,又因为 $ |\boldsymbol{a}-\boldsymbol{b}|=\sqrt{6} $ ,即 $ (\boldsymbol{a}-\boldsymbol{b})^{2}=6 $ ,则 $ {\boldsymbol{a}}^{2}-2\boldsymbol{a}\cdot \boldsymbol{b}+{\boldsymbol{b}}^{2}={\boldsymbol{b}}^{2}=6 $ ,所以 $ |\boldsymbol{b}|=\sqrt{6} $ .故选 $ \mathrm{D} $ .
8.已知向量 $ \boldsymbol{a} $ , $ \boldsymbol{b} $ 均为单位向量,且 $ \boldsymbol{a}\perp \boldsymbol{b} $ , $ |\boldsymbol{a}-\lambda \boldsymbol{b}|=\sqrt{5} $ ,则实数 $ \lambda = $ .
解析:由题意知 $ \boldsymbol{a}\perp \boldsymbol{b} $ , $ |\boldsymbol{a}-\lambda \boldsymbol{b}|=\sqrt{5} $ ,故 $ \boldsymbol{a}\cdot \boldsymbol{b}=0 $ ,且 $ |\boldsymbol{a}-\lambda \boldsymbol{b}{|}^{2}=5 $ ,即 $ {\boldsymbol{a}}^{2}-2\lambda \boldsymbol{a}\cdot \boldsymbol{b}+{\lambda }^{2}{\boldsymbol{b}}^{2}=5 $ ,故 $ 1+{\lambda }^{2}=5 $ ,解得 $ \lambda =±2 $ .
9.若非零向量 $ \overrightarrow {AB} $ 与 $ \overrightarrow {AC} $ 满足 $ (\dfrac{\overrightarrow {AB}}{|\overrightarrow {AB}|}+\dfrac{\overrightarrow {AC}}{|\overrightarrow {AC}|})\cdot \overrightarrow {BC}=0 $ , $ \dfrac{\overrightarrow {AB}}{|\overrightarrow {AB}|}\cdot \dfrac{\overrightarrow {AC}}{|\overrightarrow {AC}|}=\dfrac{1}{2} $ ,则 $ △ABC $ 为( )
A.三边均不相等的三角形
B.直角三角形
C.等腰直角三角形
D.等边三角形
答案:D
解析:显然 $ \dfrac{\overrightarrow {AB}}{|\overrightarrow {AB}|} $ , $ \dfrac{\overrightarrow {AC}}{|\overrightarrow {AC}|} $ 是与 $ \overrightarrow {AB} $ , $ \overrightarrow {AC} $ 分别同向的单位向量,由 $ (\dfrac{\overrightarrow {AB}}{|\overrightarrow {AB}|}+\dfrac{\overrightarrow {AC}}{|\overrightarrow {AC}|})\cdot \overrightarrow {BC}=0 $ ,
得 $ \mathrm{\angle }BAC $ 的平分线与 $ BC $ 垂直,于是 $ AB=AC $ ,
而 $ \dfrac{\overrightarrow {AB}}{|\overrightarrow {AB}|}\cdot \dfrac{\overrightarrow {AC}}{|\overrightarrow {AC}|}=1×1× \cos \mathrm{\angle }BAC=\dfrac{1}{2} $ ,即 $ \cos \mathrm{\angle }BAC=\dfrac{1}{2} $ .
又 $ \mathrm{\angle }BAC\in (0,\mathrm{\pi }) $ ,因此 $ \mathrm{\angle }BAC=\dfrac{\mathrm{\pi }}{3} $ ,所以 $ △ABC $ 是等边三角形.
故选 $ \mathrm{D} $ .
10.已知 $ {\boldsymbol{e}}_{1} $ , $ {\boldsymbol{e}}_{2} $ 为平面中的单位向量,且满足 $ {\boldsymbol{e}}_{1}\cdot {\boldsymbol{e}}_{2}=\dfrac{1}{4} $ ,若 $ \boldsymbol{a}=2{\boldsymbol{e}}_{1}+{\boldsymbol{e}}_{2} $ , $ \boldsymbol{b}=\lambda {\boldsymbol{e}}_{1}-{\boldsymbol{e}}_{2} $ ,且 $ \boldsymbol{a}\perp \boldsymbol{b} $ ,则实数 $ \lambda = $ .
解析:因为 $ \boldsymbol{a}\perp \boldsymbol{b} $ ,且 $ {\boldsymbol{e}}_{1}\cdot {\boldsymbol{e}}_{2}=\dfrac{1}{4} $ , $ |{\boldsymbol{e}}_{1}|=|{\boldsymbol{e}}_{2}|=1 $ ,所以 $ \boldsymbol{a}\cdot \boldsymbol{b}=(2{\boldsymbol{e}}_{1}+{\boldsymbol{e}}_{2})\cdot (\lambda {\boldsymbol{e}}_{1}-{\boldsymbol{e}}_{2})=0 $ ,
即 $ 2\lambda |{\boldsymbol{e}}_{1}{|}^{2}-2{\boldsymbol{e}}_{1}\cdot {\boldsymbol{e}}_{2}+\lambda {\boldsymbol{e}}_{1}\cdot {\boldsymbol{e}}_{2}-|{\boldsymbol{e}}_{2}{|}^{2}=0 $ ,所以 $ 2\lambda -2×\dfrac{1}{4}+\lambda ×\dfrac{1}{4}-1=0 $ ,解得 $ \lambda =\dfrac{2}{3} $ .
11.在边长为1的等边三角形 $ ABC $ 中,设 $ \overrightarrow {BC}=\boldsymbol{a} $ , $ \overrightarrow {CA}=\boldsymbol{b} $ , $ \overrightarrow {AB}=\boldsymbol{c} $ ,则 $ \boldsymbol{a}\cdot \boldsymbol{b}+\boldsymbol{b}\cdot \boldsymbol{c}+\boldsymbol{c}\cdot \boldsymbol{a}= $ ( )
A. $ -\dfrac{3}{2} $
B.0
C. $ \dfrac{3}{2} $
D.3
答案:A
解析: $ \boldsymbol{a}\cdot \boldsymbol{b}=\overrightarrow {BC}\cdot \overrightarrow {CA}=\left|\overrightarrow {BC}\right|\left|\overrightarrow {CA}\right|\cdot \cos ({180}^{\circ }-\mathrm{\angle }BCA)=-\left|\overrightarrow {BC}\right|\left|\overrightarrow {CA}\right|\cdot \cos \text{ }{60}^{\circ }=-\dfrac{1}{2} $ .同理 $ \boldsymbol{b}\cdot \boldsymbol{c}=-\dfrac{1}{2} $ , $ \boldsymbol{c}\cdot \boldsymbol{a}=-\dfrac{1}{2} $ ,则 $ \boldsymbol{a}\cdot \boldsymbol{b}+\boldsymbol{b}\cdot \boldsymbol{c}+\boldsymbol{c}\cdot \boldsymbol{a}=-\dfrac{3}{2} $ .
12.已知 $ |\boldsymbol{a}|=2 $ , $ |\boldsymbol{b}|=3 $ , $ \boldsymbol{a} $ 与 $ \boldsymbol{b} $ 的夹角为 $ {60}^{\circ } $ .若 $ \boldsymbol{a}+\lambda \boldsymbol{b} $ 与 $ \lambda \boldsymbol{a}+\boldsymbol{b} $ 的夹角为锐角,则实数 $ \lambda $ 的取值范围为 .
答案: $ (-\mathrm{\infty },\dfrac{-13-\sqrt{133}}{6})\cup (\dfrac{\sqrt{133}-13}{6},1)\cup (1,+\mathrm{\infty }) $
解析:由题意可得 $ \boldsymbol{a}\cdot \boldsymbol{b}=|\boldsymbol{a}||\boldsymbol{b}|\cdot \cos {60}^{\circ }=2×3×\dfrac{1}{2}=3 $ .又 $ \because (\boldsymbol{a}+\lambda \boldsymbol{b})\cdot (\lambda \boldsymbol{a}+\boldsymbol{b})=\lambda {\boldsymbol{a}}^{2}+({\lambda }^{2}+1)\boldsymbol{a}\cdot \boldsymbol{b}+\lambda {\boldsymbol{b}}^{2} $ , $ \boldsymbol{a}+\lambda \boldsymbol{b} $ 与 $ \lambda \boldsymbol{a}+\boldsymbol{b} $ 的夹角为锐角, $ \therefore \lambda {\boldsymbol{a}}^{2}+({\lambda }^{2}+1)\boldsymbol{a}\cdot \boldsymbol{b}+\lambda {\boldsymbol{b}}^{2} > 0.\because {\boldsymbol{a}}^{2}=|\boldsymbol{a}{|}^{2}=4 $ , $ {\boldsymbol{b}}^{2}=|\boldsymbol{b}{|}^{2}=9 $ , $ \boldsymbol{a}\cdot \boldsymbol{b}=3 $ , $ \therefore 3{\lambda }^{2}+13\lambda +3 > 0 $ ,解得 $ \lambda < \dfrac{-13-\sqrt{133}}{6} $ 或 $ \lambda > \dfrac{\sqrt{133}-13}{6} $ .当 $ \lambda =1 $ 时, $ \boldsymbol{a}+\lambda \boldsymbol{b} $ 与 $ \lambda \boldsymbol{a}+\boldsymbol{b} $ 共线,其夹角不为锐角,故实数 $ \lambda $ 的取值范围为 $ (-\mathrm{\infty } $ , $ \dfrac{-13-\sqrt{133}}{6})\cup (\dfrac{\sqrt{133}-13}{6} $ , $ 1 )\cup (1,+\mathrm{\infty } ) $ .
二、刷提升
1.已知向量 $ \boldsymbol{a} $ 和 $ \boldsymbol{b} $ 满足 $ |\boldsymbol{a}|=2 $ , $ |\boldsymbol{b}|=1 $ , $ (2\boldsymbol{a}+\boldsymbol{b})\cdot (\boldsymbol{a}+\boldsymbol{b})=6 $ ,则向量 $ \boldsymbol{a}-\boldsymbol{b} $ 在向量 $ \boldsymbol{a} $ 上的投影向量为( )
A. $ \dfrac{5}{4}\boldsymbol{a} $
B. $ -\dfrac{5}{4}\boldsymbol{a} $
C. $ \dfrac{3}{4}\boldsymbol{a} $
D. $ -\dfrac{3}{4}\boldsymbol{a} $
答案:A
解析: $ (2\boldsymbol{a}+\boldsymbol{b})\cdot (\boldsymbol{a}+\boldsymbol{b})=2{\boldsymbol{a}}^{2}+{\boldsymbol{b}}^{2}+3\boldsymbol{a}\cdot \boldsymbol{b}=8+1+3\boldsymbol{a}\cdot \boldsymbol{b}=6⇒\boldsymbol{a}\cdot \boldsymbol{b}=-1 $ ,
向量 $ \boldsymbol{a}-\boldsymbol{b} $ 在向量 $ \boldsymbol{a} $ 上的投影向量为 $ \dfrac{(\boldsymbol{a}-\boldsymbol{b})\cdot \boldsymbol{a}}{|\boldsymbol{a}|}\cdot \dfrac{\boldsymbol{a}}{|\boldsymbol{a}|}=\dfrac{{\boldsymbol{a}}^{2}-\boldsymbol{a}\cdot \boldsymbol{b}}{|\boldsymbol{a}{|}^{2}}\cdot \boldsymbol{a}=\dfrac{5}{4}\boldsymbol{a} $ ,故选 $ \mathrm{A} $ .
2.如图,已知平行四边形 $ ABCD $ 中, $ AB=3 $ , $ AD=2 $ , $ \mathrm{\angle }BAD=\dfrac{\mathrm{\pi }}{3} $ , $ M $ , $ P $ 分别是 $ AB $ , $ BC $ 的中点, $ N $ 是 $ DC $ 上一点,且 $ DN=\dfrac{2}{3}DC $ ,则 $ \overrightarrow {AP}\cdot \overrightarrow {MN}= $ ( )
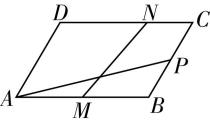
A. $ \dfrac{9}{2} $
B. $ \dfrac{11}{2} $
C. $ \dfrac{23}{4} $
D. $ \dfrac{27}{4} $
答案:D
解析:平行四边形 $ ABCD $ 中, $ AB=3 $ , $ AD=2 $ , $ \mathrm{\angle }BAD=\dfrac{\mathrm{\pi }}{3} $ , $ M $ , $ P $ 分别是 $ AB $ , $ BC $ 的中点, $ N $ 是 $ DC $ 上一点,且 $ DN=\dfrac{2}{3}DC $ ,
则 $ \overrightarrow {AP}\cdot \overrightarrow {MN}=(\overrightarrow {AB}+\dfrac{1}{2}\overrightarrow {AD})\cdot (\overrightarrow {AN}-\overrightarrow {AM})=(\overrightarrow {AB}+\dfrac{1}{2}\overrightarrow {AD})\cdot (\dfrac{2}{3}\overrightarrow {AB}+\overrightarrow {AD}-\dfrac{1}{2}\overrightarrow {AB})=(\overrightarrow {AB}+\dfrac{1}{2}\overrightarrow {AD})\cdot (\dfrac{1}{6}\overrightarrow {AB}+\overrightarrow {AD})=\dfrac{1}{6}{\overrightarrow {AB}}^{2}+\dfrac{13}{12}\overrightarrow {AB}\cdot \overrightarrow {AD}+\dfrac{1}{2}{\overrightarrow {AD}}^{2}=\dfrac{1}{6}×9+\dfrac{13}{12}×3×2×\dfrac{1}{2}+\dfrac{1}{2}×4=\dfrac{27}{4} $ .故选 $ \mathrm{D} $ .
3.已知平面向量 $ \boldsymbol{a} $ , $ \boldsymbol{b} $ 满足 $ |\boldsymbol{a}|=\sqrt{3} $ , $ |\boldsymbol{b}|=1 $ , $ (\boldsymbol{a}+\boldsymbol{b})\perp (\boldsymbol{a}+3\boldsymbol{b}) $ ,则向量 $ \boldsymbol{a} $ 与 $ \boldsymbol{b} $ 的夹角为( )
A. $ \dfrac{5\mathrm{\pi }}{6} $
B. $ \dfrac{2\mathrm{\pi }}{3} $
C. $ \dfrac{\mathrm{\pi }}{3} $
D. $ \dfrac{\mathrm{\pi }}{6} $
答案:A
解析:由 $ (\boldsymbol{a}+\boldsymbol{b})\perp (\boldsymbol{a}+3\boldsymbol{b}) $ 可得 $ (\boldsymbol{a}+\boldsymbol{b})\cdot (\boldsymbol{a}+3\boldsymbol{b})={\boldsymbol{a}}^{2}+4\boldsymbol{a}\cdot \boldsymbol{b}+3{\boldsymbol{b}}^{2}=3+4\boldsymbol{a}\cdot \boldsymbol{b}+3=0 $ ,
故 $ \boldsymbol{a}\cdot \boldsymbol{b}=-\dfrac{3}{2} $ ,因此 $ \cos ⟨\boldsymbol{a} $ , $ \boldsymbol{b}⟩=\dfrac{\boldsymbol{a}\cdot \boldsymbol{b}}{|\boldsymbol{a}||\boldsymbol{b}|}=\dfrac{-\dfrac{3}{2}}{\sqrt{3}}=-\dfrac{\sqrt{3}}{2} $ ,
$ \because ⟨\boldsymbol{a} $ , $ \boldsymbol{b}⟩\in [0,\mathrm{\pi }] $ , $ \therefore ⟨\boldsymbol{a} $ , $ \boldsymbol{b}⟩=\dfrac{5\mathrm{\pi }}{6} $ ,故选 $ \mathrm{A} $ .
4.在 $ △ABC $ 中,若动点 $ P $ 满足 $ {\overrightarrow {AB}}^{2}-{\overrightarrow {AC}}^{2}=2\overrightarrow {CB}\cdot \overrightarrow {AP} $ ,则点 $ P $ 的轨迹一定经过 $ △ABC $ 的( )
A.重心
B.垂心
C.外心
D.内心
答案:C
解析:因为 $ {\overrightarrow {AB}}^{2}-{\overrightarrow {AC}}^{2}=(\overrightarrow {AB}+\overrightarrow {AC})\cdot (\overrightarrow {AB}-\overrightarrow {AC})=(\overrightarrow {AB}+\overrightarrow {AC})\cdot \overrightarrow {CB}=2\overrightarrow {CB}\cdot \overrightarrow {AP} $ ,
所以 $ \overrightarrow {CB}\cdot (\overrightarrow {AB}+\overrightarrow {AC}-2\overrightarrow {AP})=\overrightarrow {CB}\cdot (\overrightarrow {PB}+\overrightarrow {PC})=0 $ .
设 $ BC $ 的中点为 $ D $ ,则 $ \overrightarrow {PB}+\overrightarrow {PC}=2\overrightarrow {PD} $ ,则 $ \overrightarrow {CB}\cdot 2\overrightarrow {PD}=0 $ ,
即 $ \overrightarrow {CB}\cdot \overrightarrow {PD}=0 $ ,所以 $ \overrightarrow {CB}\perp \overrightarrow {PD} $ ,所以点 $ P $ 在线段 $ BC $ 的垂直平分线上,
故点 $ P $ 的轨迹经过 $ △ABC $ 的外心.
故选 $ \mathrm{C} $ .
5.如图,已知正方形 $ ABCD $ 的边长为4,若动点 $ P $ 在以 $ AB $ 为直径的半圆上(正方形 $ ABCD $ 内部,含边界),则 $ \overrightarrow {PC}\cdot \overrightarrow {PD} $ 的取值范围为( )
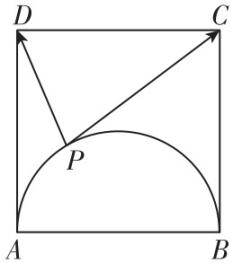
A. $ (0,16) $
B. $ [0,16] $
C. $ (0,4) $
D. $ [0,4] $
答案:B
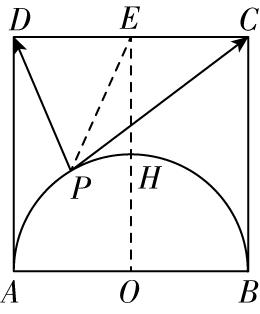
解析:取 $ CD $ 的中点 $ E $ ,连接 $ PE $ ,如图,
则 $ \overrightarrow {PC}+\overrightarrow {PD}=2\overrightarrow {PE} $ , $ \overrightarrow {PC}-\overrightarrow {PD}=\overrightarrow {DC}=2\overrightarrow {DE} $ ,
两式分别平方再相减得 $ \overrightarrow {PC}\cdot \overrightarrow {PD}={\overrightarrow {PE}}^{2}-{\overrightarrow {DE}}^{2}={|\overrightarrow {PE}|}^{2}-4 $ .
设 $ AB $ 的中点为 $ O $ ,连接 $ OE $ 交圆弧于点 $ H $ ,则当 $ P $ 与 $ H $ 重合时, $ PE $ 最小,最小值为2,
当 $ P $ 与 $ A $ 或 $ B $ 重合时, $ PE $ 最大,最大值为 $ \sqrt{{4}^{2}+{2}^{2}}=2\sqrt{5} $ ,
所以 $ \overrightarrow {PC}\cdot \overrightarrow {PD}\in [{2}^{2}-4, (2\sqrt{5})^{2}-4 ]= [0,16 ] $ .故选 $ \mathrm{B} $ .
6.已知 $ △ABC $ 的外接圆圆心为 $ O $ ,且 $ \overrightarrow {OA}\cdot \overrightarrow {OC}+\overrightarrow {OA}\cdot \overrightarrow {OB}={\overrightarrow {OA}}^{2}+\overrightarrow {OB}\cdot \overrightarrow {OC} $ , $ |\overrightarrow {OC}|=|\overrightarrow {AB}| $ ,则向量 $ \overrightarrow {AB} $ 在向量 $ \overrightarrow {BC} $ 上的投影向量为( )
A. $ \dfrac{1}{4}\overrightarrow {BC} $
B. $ \dfrac{\sqrt{3}}{4}\overrightarrow {BC} $
C. $ -\dfrac{1}{4}\overrightarrow {BC} $
D. $ -\dfrac{\sqrt{3}}{4}\overrightarrow {BC} $
答案:C
解析:由 $ \overrightarrow {OA}\cdot \overrightarrow {OC}+\overrightarrow {OA}\cdot \overrightarrow {OB}={\overrightarrow {OA}}^{2}+\overrightarrow {OB}\cdot \overrightarrow {OC}⇒\overrightarrow {OA}\cdot \overrightarrow {OC}-{\overrightarrow {OA}}^{2}+\overrightarrow {OA}\cdot \overrightarrow {OB}-\overrightarrow {OB}\cdot \overrightarrow {OC}=0⇒\overrightarrow {OA}\cdot (\overrightarrow {OC}-\overrightarrow {OA})-\overrightarrow {OB}\cdot (\overrightarrow {OC}-\overrightarrow {OA})=0⇒(\overrightarrow {OA}-\overrightarrow {OB})\cdot (\overrightarrow {OC}-\overrightarrow {OA})=0 $ ,
即 $ \overrightarrow {BA}\cdot \overrightarrow {AC}=0 $ ,所以 $ \overrightarrow {BA}\perp \overrightarrow {AC} $ ,作图如下.
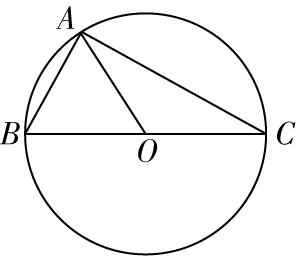
由图可知, $ △ABC $ 的外接圆圆心 $ O $ 即为 $ BC $ 的中点,
又因为 $ |\overrightarrow {OC}|=|\overrightarrow {AB}| $ ,所以 $ |\overrightarrow {BC}|=2|\overrightarrow {AB}| $ ,则 $ \mathrm{\angle }ACB=\dfrac{\mathrm{\pi }}{6} $ , $ \mathrm{\angle }ABC=\dfrac{\mathrm{\pi }}{3} $ ,
所以向量 $ \overrightarrow {AB} $ 在向量 $ \overrightarrow {BC} $ 上的投影向量为 $ |\overrightarrow {AB}| \cos \dfrac{2\mathrm{\pi }}{3}\cdot \dfrac{\overrightarrow {BC}}{|\overrightarrow {BC}|}=|\overrightarrow {AB}| \cos \dfrac{2\mathrm{\pi }}{3}\cdot \dfrac{\overrightarrow {BC}}{2|\overrightarrow {AB}|}=-\dfrac{1}{4}\overrightarrow {BC} $ .故选 $ \mathrm{C} $ .
7.已知非零向量 $ \boldsymbol{a} $ , $ \boldsymbol{b} $ 满足 $ |\boldsymbol{a}|=4 $ , $ |\boldsymbol{a}+t\boldsymbol{b}|(t\in \boldsymbol{R}) $ 的最小值为2,则 $ \boldsymbol{a} $ , $ \boldsymbol{b} $ 的夹角为( )
A. $ \dfrac{\mathrm{\pi }}{3} $
B. $ \dfrac{\mathrm{\pi }}{6} $
C. $ \dfrac{\mathrm{\pi }}{6} $ 或 $ \dfrac{5\mathrm{\pi }}{6} $
D. $ \dfrac{\mathrm{\pi }}{3} $ 或 $ \dfrac{2\mathrm{\pi }}{3} $
答案:C
解析:设 $ \boldsymbol{a} $ , $ \boldsymbol{b} $ 的夹角为 $ \theta $ , $ 0\leqslant \theta \leqslant \mathrm{\pi } $ ,非零向量 $ \boldsymbol{a} $ , $ \boldsymbol{b} $ 满足 $ |\boldsymbol{a}|=4 $ , $ |\boldsymbol{a}+t\boldsymbol{b}|(t\in \boldsymbol{R}) $ 的最小值为2,所以 $ {\boldsymbol{a}}^{2}+2t\boldsymbol{a}\cdot \boldsymbol{b}+{t}^{2}{\boldsymbol{b}}^{2}={t}^{2}{\boldsymbol{b}}^{2}+8t|\boldsymbol{b}| \cos \theta +16 $ 的最小值为 $ \dfrac{4×{\boldsymbol{b}}^{2}×16-(8|\boldsymbol{b}| \cos \theta )^{2}}{4×{\boldsymbol{b}}^{2}}=16-16{ \cos }^{2}\theta =4 $ ,可得 $ { \cos }^{2}\theta =\dfrac{3}{4} $ ,故 $ \cos \theta =±\dfrac{\sqrt{3}}{2} $ ,可得 $ \theta =\dfrac{\mathrm{\pi }}{6} $ 或 $ \theta =\dfrac{5\mathrm{\pi }}{6} $ .故选 $ \mathrm{C} $ .
8.如图,在 $ △ABC $ 中, $ \overrightarrow {AD}=2\overrightarrow {DB} $ , $ \overrightarrow {AE}=\overrightarrow {EC} $ ,点 $ F $ , $ G $ 分别是 $ DE $ , $ BC $ 的中点,连接 $ FG $ .
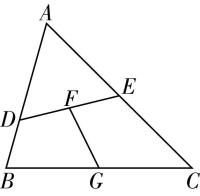
(1) 试用 $ \overrightarrow {AB} $ 和 $ \overrightarrow {AC} $ 表示 $ \overrightarrow {FG} $ .
(2) 若 $ AB=6 $ , $ AC=8 $ , $ \mathrm{\angle }BAC={60}^{\circ } $ .
① 求 $ |\overrightarrow {FG}| $ ;
② 求 $ \cos \mathrm{\angle }BGF $ .
答案:(1) 【解】在四边形 $ FDBG $ 中, $ \overrightarrow {FG}=\overrightarrow {FD}+\overrightarrow {DB}+\overrightarrow {BG} $ .
在四边形 $ FECG $ 中, $ \overrightarrow {FG}=\overrightarrow {FE}+\overrightarrow {EC}+\overrightarrow {CG} $ .
又因为 $ F $ , $ G $ 分别是 $ DE $ , $ BC $ 的中点,所以 $ \overrightarrow {FD}=-\overrightarrow {FE} $ , $ \overrightarrow {BG}=-\overrightarrow {CG} $ .
所以 $ 2\overrightarrow {FG}=\overrightarrow {FD}+\overrightarrow {DB}+\overrightarrow {BG}+\overrightarrow {FE}+\overrightarrow {EC}+\overrightarrow {CG}=\overrightarrow {DB}+\overrightarrow {EC} $ ,即 $ \overrightarrow {FG}=\dfrac{1}{2}\overrightarrow {DB}+\dfrac{1}{2}\overrightarrow {EC} $ ,
又因为 $ \overrightarrow {AD}=2\overrightarrow {DB} $ , $ \overrightarrow {AE}=\overrightarrow {EC} $ ,所以 $ \overrightarrow {DB}=\dfrac{1}{3}\overrightarrow {AB} $ , $ \overrightarrow {EC}=\dfrac{1}{2}\overrightarrow {AC} $ .
所以 $ \overrightarrow {FG}=\dfrac{1}{2}×\dfrac{1}{3}\overrightarrow {AB}+\dfrac{1}{2}×\dfrac{1}{2}\overrightarrow {AC}=\dfrac{1}{6}\overrightarrow {AB}+\dfrac{1}{4}\overrightarrow {AC} $ .
(2) ① 由题知 $ \overrightarrow {AB}\cdot \overrightarrow {AC}=6×8× \cos {60}^{\circ }=24 $ .
又由(1)知, $ \overrightarrow {FG}=\dfrac{1}{6}\overrightarrow {AB}+\dfrac{1}{4}\overrightarrow {AC} $ .
因此 $ {|\overrightarrow {FG}|}^{2}=\dfrac{1}{36}{\overrightarrow {AB}}^{2}+\dfrac{1}{16}{\overrightarrow {AC}}^{2}+\dfrac{1}{12}\overrightarrow {AB}\cdot \overrightarrow {AC}=\dfrac{1}{36}×{6}^{2}+\dfrac{1}{16}×{8}^{2}+\dfrac{1}{12}×24=7 $ .
所以 $ |\overrightarrow {FG}|=\sqrt{7} $ .
② 因为 $ \overrightarrow {BG}=\dfrac{1}{2}\overrightarrow {BC}=\dfrac{1}{2}\overrightarrow {AC}-\dfrac{1}{2}\overrightarrow {AB} $ .
所以 $ |\overrightarrow {BG}|=\sqrt{{\left(\dfrac{1}{2}\overrightarrow {AC}-\dfrac{1}{2}\overrightarrow {AB}\right) ^ {2}}} $
$ =\dfrac{1}{2}\sqrt{{\overrightarrow {AC}}^{2}+{\overrightarrow {AB}}^{2}-2\overrightarrow {AB}\cdot \overrightarrow {AC}} $
$ =\dfrac{1}{2}\sqrt{{8}^{2}+{6}^{2}-2×24}=\sqrt{13} $ .
$ \overrightarrow {FG}\cdot \overrightarrow {BG}=(\dfrac{1}{6}\overrightarrow {AB}+\dfrac{1}{4}\overrightarrow {AC})\cdot (\dfrac{1}{2}\overrightarrow {AC}-\dfrac{1}{2}\overrightarrow {AB}) $
$ =\dfrac{1}{8}{\overrightarrow {AC}}^{2}-\dfrac{1}{12}{\overrightarrow {AB}}^{2}-\dfrac{1}{24}\overrightarrow {AB}\cdot \overrightarrow {AC} $
$ =\dfrac{1}{8}×{8}^{2}-\dfrac{1}{12}×{6}^{2}-\dfrac{1}{24}×24=4 $ ,
所以 $ \cos \mathrm{\angle }BGF=\dfrac{\overrightarrow {FG}\cdot \overrightarrow {BG}}{|\overrightarrow {FG}||\overrightarrow {BG}|}=\dfrac{4}{\sqrt{7}×\sqrt{13}}=\dfrac{4\sqrt{91}}{91} $ .
解析:
9.如图,在平面四边形 $ ABCD $ 中,已知 $ \overrightarrow {CD}=2\overrightarrow {BA} $ , $ |\overrightarrow {BC}|=|\overrightarrow {CD}|=2 $ , $ \overrightarrow {BA}\cdot \overrightarrow {BC}=\sqrt{2} $ ,若 $ \overrightarrow {BO}=\lambda \overrightarrow {BC}(\lambda \in \boldsymbol{R}) $ .
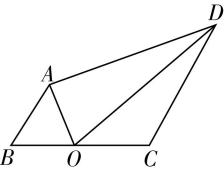
(1) 当 $ \lambda =\dfrac{1}{2} $ 时,求 $ \overrightarrow {OA}\cdot \overrightarrow {OD} $ 的值;
(2) 求 $ \overrightarrow {OA}\cdot \overrightarrow {OD} $ 取得最小值时 $ \lambda $ 的值.
答案:(1) 【解】当 $ \lambda =\dfrac{1}{2} $ 时, $ O $ 为线段 $ BC $ 的中点,
则 $ \overrightarrow {OB}=-\overrightarrow {OC} $ , $ \overrightarrow {OA}=\overrightarrow {OB}+\overrightarrow {BA} $ , $ \overrightarrow {OD}=\overrightarrow {OC}+\overrightarrow {CD}=-\overrightarrow {OB}+2\overrightarrow {BA} $ ,
从而 $ \overrightarrow {OA}\cdot \overrightarrow {OD}=-{\overrightarrow {OB}}^{2}+\overrightarrow {OB}\cdot \overrightarrow {BA}+2{\overrightarrow {BA}}^{2} $ ,
又因为 $ \overrightarrow {BA}\cdot \overrightarrow {BC}=\sqrt{2} $ , $ \overrightarrow {OB}=-\dfrac{1}{2}\overrightarrow {BC} $ ,所以 $ \overrightarrow {OB}\cdot \overrightarrow {BA}=-\dfrac{\sqrt{2}}{2} $ ,
从而 $ \overrightarrow {OA}\cdot \overrightarrow {OD}=-{\overrightarrow {OB}}^{2}+\overrightarrow {OB}\cdot \overrightarrow {BA}+2{\overrightarrow {BA}}^{2}=1-\dfrac{\sqrt{2}}{2} $ .
(2) 因为 $ \overrightarrow {BO}=\lambda \overrightarrow {BC} $ ,所以 $ \overrightarrow {OC}=(1-\lambda )\overrightarrow {BC} $ ,
$ \overrightarrow {OA}=\overrightarrow {OB}+\overrightarrow {BA}=-\lambda \overrightarrow {BC}+\overrightarrow {BA} $ , $ \overrightarrow {OD}=\overrightarrow {OC}+\overrightarrow {CD}=(1-\lambda )\overrightarrow {BC}+2\overrightarrow {BA} $ ,
从而 $ \overrightarrow {OA}\cdot \overrightarrow {OD}=-\lambda (1-\lambda ){\overrightarrow {BC}}^{2}+(1-3\lambda )\cdot \overrightarrow {BC}\cdot \overrightarrow {BA}+2{\overrightarrow {BA}}^{2} $
$ =-4\lambda (1-\lambda )+\sqrt{2}(1-3\lambda )+2=4{\lambda }^{2}-(4+3\sqrt{2})\lambda +2+\sqrt{2}\geqslant -\dfrac{1+4\sqrt{2}}{8} $ ,
当且仅当 $ \lambda =\dfrac{4+3\sqrt{2}}{8} $ 时, $ \overrightarrow {OA}\cdot \overrightarrow {OD} $ 取得最小值.
解析:







