6.3.1 平面向量基本定理
一、刷基础
1.设{ $ {\boldsymbol{e}}_{1} $ , $ {\boldsymbol{e}}_{2}} $ 是平面内所有向量的一个基底,则下列四组向量中不能作为一个基底的是( )
A.{ $ {\boldsymbol{e}}_{1}+{\boldsymbol{e}}_{2} $ , $ {\boldsymbol{e}}_{1}-{\boldsymbol{e}}_{2}} $
B. $ {3{\boldsymbol{e}}_{1}-4{\boldsymbol{e}}_{2} $ , $ 6{\boldsymbol{e}}_{1}-8{\boldsymbol{e}}_{2}} $
C.{ $ {\boldsymbol{e}}_{1}+2{\boldsymbol{e}}_{2} $ , $ 2{\boldsymbol{e}}_{1}+{\boldsymbol{e}}_{2}} $
D.{ $ {\boldsymbol{e}}_{1} $ , $ 5{\boldsymbol{e}}_{2}} $
答案:B
解析:选项 $ \mathrm{B} $ 中, $ 6{\boldsymbol{e}}_{1}-8{\boldsymbol{e}}_{2}=2(3{\boldsymbol{e}}_{1}-4{\boldsymbol{e}}_{2}) $ , $ \therefore 6{\boldsymbol{e}}_{1}-8{\boldsymbol{e}}_{2} $ 与 $ 3{\boldsymbol{e}}_{1}-4{\boldsymbol{e}}_{2} $ 共线, $ \therefore $ 不能作为一个基底,选项 $ \mathrm{A} $ , $ \mathrm{C} $ , $ \mathrm{D} $ 中两向量均不共线,可作为一个基底.
故选 $ \mathrm{B} $ .
2.如果{ $ {\boldsymbol{e}}_{1} $ , $ {\boldsymbol{e}}_{2} $ }是某一平面内所有向量的一个基底,那么下列说法正确的是( )
A.若存在实数 $ {\lambda }_{1} $ , $ {\lambda }_{2} $ 使 $ {\lambda }_{1}{\boldsymbol{e}}_{1}+{\lambda }_{2}{\boldsymbol{e}}_{2}=0 $ 成立,则 $ {\lambda }_{1}={\lambda }_{2}\ne 0 $
B.该平面内任意向量 $ \boldsymbol{a} $ 都可以表示为 $ \boldsymbol{a}={\lambda }_{1}{\boldsymbol{e}}_{1}+{\lambda }_{2}{\boldsymbol{e}}_{2} $ ,其中 $ {\lambda }_{1} $ , $ {\lambda }_{2}\in \boldsymbol{R} $
C. $ {\lambda }_{1}{\boldsymbol{e}}_{1}+{\lambda }_{2}{\boldsymbol{e}}_{2}({\lambda }_{1},{\lambda }_{2}\in \boldsymbol{R}) $ 不一定在该平面内
D.对于该平面内任意向量 $ \boldsymbol{a} $ ,使 $ \boldsymbol{a}={\lambda }_{1}{\boldsymbol{e}}_{1}+{\lambda }_{2}{\boldsymbol{e}}_{2} $ 的实数 $ {\lambda }_{1} $ , $ {\lambda }_{2} $ 有无数对
答案:B
解析:对于 $ \mathrm{A} $ ,因为{ $ {\boldsymbol{e}}_{1} $ , $ {\boldsymbol{e}}_{2} $ }是某一平面内所有向量的一个基底,所以 $ {\boldsymbol{e}}_{1} $ , $ {\boldsymbol{e}}_{2} $ 不共线.根据向量共线的充要条件可得,若存在实数 $ {\lambda }_{1} $ , $ {\lambda }_{2} $ 使 $ {\lambda }_{1}{\boldsymbol{e}}_{1}+{\lambda }_{2}{\boldsymbol{e}}_{2}=0 $ 成立,则 $ {\lambda }_{1}={\lambda }_{2}=0 $ ,故 $ \mathrm{A} $ 错误;
对于 $ \mathrm{B} $ ,根据平面向量基本定理可判断 $ \mathrm{B} $ 正确;
对于 $ \mathrm{C} $ ,根据平面向量基本定理可得, $ {\lambda }_{1}{\boldsymbol{e}}_{1}+{\lambda }_{2}{\boldsymbol{e}}_{2}({\lambda }_{1},{\lambda }_{2}\in \boldsymbol{R}) $ 一定在该平面内,故 $ \mathrm{C} $ 错误;
对于 $ \mathrm{D} $ ,根据平面向量基本定理可得,对于该平面内任意向量 $ \boldsymbol{a} $ ,使 $ \boldsymbol{a}={\lambda }_{1}{\boldsymbol{e}}_{1}+{\lambda }_{2}{\boldsymbol{e}}_{2} $ 的实数 $ {\lambda }_{1} $ , $ {\lambda }_{2} $ 有且只有一对,故 $ \mathrm{D} $ 错误 .
故选 $ \mathrm{B} $ .
3.如图所示,平面内的两条相交直线 $ O{P}_{1} $ 和 $ O{P}_{2} $ 将该平面分割成四个部分Ⅰ,Ⅱ,Ⅲ,Ⅳ(不包括边界).若 $ \overrightarrow {OP}=a\overrightarrow {O{P}_{1}}+b\overrightarrow {O{P}_{2}} $ ,且点 $ P $ 落在第Ⅲ部分,则实数 $ a $ , $ b $ 满足( )
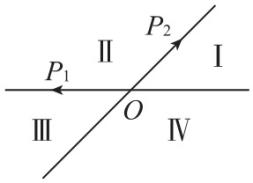
A. $ a > 0 $ , $ b > 0 $
B. $ a > 0 $ , $ b < 0 $
C. $ a < 0 $ , $ b > 0 $
D. $ a < 0 $ , $ b < 0 $
答案:B
解析:取第Ⅲ部分内一点画图易得 $ a > 0 $ , $ b < 0 $ .
4.在平行四边形 $ ABCD $ 中, $ \overrightarrow {AM}=3\overrightarrow {MD} $ , $ \overrightarrow {DN}=5\overrightarrow {NB} $ ,记 $ \overrightarrow {AB}=\boldsymbol{a} $ , $ \overrightarrow {AD}=\boldsymbol{b} $ ,则 $ \overrightarrow {MN}= $ ( )
A. $ \dfrac{3}{4}\boldsymbol{a}+\dfrac{5}{12}\boldsymbol{b} $
B. $ \dfrac{5}{6}\boldsymbol{a}-\dfrac{7}{12}\boldsymbol{b} $
C. $ \dfrac{5}{6}\boldsymbol{a}+\dfrac{7}{12}\boldsymbol{b} $
D. $ \dfrac{3}{4}\boldsymbol{a}-\dfrac{5}{12}\boldsymbol{b} $
答案:B
解析:如图,连接 $ AN $ ,由题知 $ \overrightarrow {MN}=\overrightarrow {MA}+\overrightarrow {AN}=\overrightarrow {AN}-\dfrac{3}{4}\overrightarrow {AD} $ ,
其中 $ \overrightarrow {AN}=\overrightarrow {AD}+\overrightarrow {DN}=\overrightarrow {AD}+\dfrac{5}{6}\overrightarrow {DB}=\overrightarrow {AD}+\dfrac{5}{6}(\overrightarrow {AB}-\overrightarrow {AD})=\dfrac{5}{6}\overrightarrow {AB}+\dfrac{1}{6}\overrightarrow {AD} $ ,
故 $ \overrightarrow {MN}=\dfrac{5}{6}\overrightarrow {AB}+\dfrac{1}{6}\overrightarrow {AD}-\dfrac{3}{4}\overrightarrow {AD}=\dfrac{5}{6}\overrightarrow {AB}-\dfrac{7}{12}\overrightarrow {AD}=\dfrac{5}{6}\boldsymbol{a}-\dfrac{7}{12}\boldsymbol{b} $ .故选 $ \mathrm{B} $ .

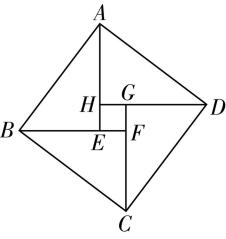
5.“赵爽弦图”是由四个全等的直角三角形与一个小正方形拼成的一个大正方形.如图,在“赵爽弦图”中,若 $ \overrightarrow {BC}=\boldsymbol{a} $ , $ \overrightarrow {BA}=\boldsymbol{b} $ , $ \overrightarrow {BE}=3\overrightarrow {EF} $ ,则 $ \overrightarrow {BF}= $ ( )

A. $ \dfrac{12}{25}\boldsymbol{a}+\dfrac{9}{25}\boldsymbol{b} $
B. $ \dfrac{16}{25}\boldsymbol{a}+\dfrac{12}{25}\boldsymbol{b} $
C. $ \dfrac{4}{5}\boldsymbol{a}+\dfrac{3}{5}\boldsymbol{b} $
D. $ \dfrac{3}{5}\boldsymbol{a}+\dfrac{4}{5}\boldsymbol{b} $
答案:B
解析:如图,因为 $ \overrightarrow {BE}=3\overrightarrow {EF} $ ,所以 $ \overrightarrow {BE}=\dfrac{3}{4}\overrightarrow {BF} $ , $ \overrightarrow {CF}=-\overrightarrow {AH}=-\dfrac{3}{4}\overrightarrow {AE} $ ,
所以 $ \overrightarrow {BF}=\boldsymbol{a}+\overrightarrow {CF}=\boldsymbol{a}-\dfrac{3}{4}\overrightarrow {AE}① $ ,
$ \overrightarrow {BE}=\dfrac{3}{4}\overrightarrow {BF}=\boldsymbol{b}+\overrightarrow {AE}② $ ,
由 $ ①+\dfrac{3}{4}×② $ 得 $ \dfrac{25}{16}\overrightarrow {BF}=\boldsymbol{a}+\dfrac{3}{4}\boldsymbol{b} $ ,
即 $ \overrightarrow {BF}=\dfrac{16}{25}\boldsymbol{a}+\dfrac{12}{25}\boldsymbol{b} $ .
故选 $ \mathrm{B} $ .
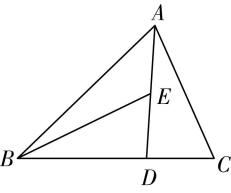
6.如图,在 $ △ABC $ 中, $ D $ 是 $ BC $ 边上靠近点 $ C $ 的三等分点, $ E $ 为 $ AD $ 中点.若 $ \overrightarrow {BE}=x\overrightarrow {AB}+y\overrightarrow {AC} $ ,则 $ x= $ ( )
A. $ \dfrac{2}{3} $
B. $ -\dfrac{4}{5} $
C. $ -\dfrac{5}{6} $
D. $ \dfrac{6}{7} $
答案:C
解析:已知 $ D $ 是 $ BC $ 边上靠近点 $ C $ 的三等分点,所以 $ \overrightarrow {AD}=\dfrac{1}{3}\overrightarrow {AB}+\dfrac{2}{3}\overrightarrow {AC} $ .
又 $ E $ 为 $ AD $ 中点,所以 $ \overrightarrow {BE}=\overrightarrow {AE}-\overrightarrow {AB}=\dfrac{1}{2}\overrightarrow {AD}-\overrightarrow {AB}=\dfrac{1}{2}(\dfrac{1}{3}\overrightarrow {AB}+\dfrac{2}{3}\overrightarrow {AC})-\overrightarrow {AB}=-\dfrac{5}{6}\overrightarrow {AB}+\dfrac{1}{3}\overrightarrow {AC} $ ,所以 $ x=-\dfrac{5}{6} $ ,故选 $ \mathrm{C} $ .
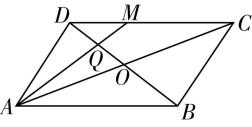
7.在平行四边形 $ ABCD $ 中, $ \overrightarrow {CM}=2\overrightarrow {MD} $ , $ AM $ 交 $ BD $ 于点 $ Q $ ,若 $ \overrightarrow {AQ}=\lambda \overrightarrow {AD}+\mu \overrightarrow {AC} $ ,则 $ \lambda +\mu = $ .
解析:如图,在 $ ▱ABCD $ 中, $ DM//AB $ ,则 $ △DQM\sim △BQA $ .
因为 $ \overrightarrow {CM}=2\overrightarrow {MD} $ ,所以 $ \overrightarrow {DM}=\dfrac{1}{3}\overrightarrow {DC} $ .又 $ \overrightarrow {AB}=\overrightarrow {DC} $ ,所以 $ \overrightarrow {DM}=\dfrac{1}{3}\overrightarrow {AB} $ ,所以 $ \dfrac{DM}{AB}=\dfrac{QM}{AQ}=\dfrac{1}{3} $ ,
故 $ \overrightarrow {AQ}=\dfrac{3}{4}\overrightarrow {AM}=\dfrac{3}{4}(\overrightarrow {AD}+\overrightarrow {DM})=\dfrac{3}{4}\overrightarrow {AD}+\dfrac{3}{4}×\dfrac{1}{3}\overrightarrow {DC}=\dfrac{3}{4}\overrightarrow {AD}+\dfrac{1}{4}(\overrightarrow {AC}-\overrightarrow {AD})=\dfrac{1}{2}\overrightarrow {AD}+\dfrac{1}{4}\overrightarrow {AC} $ ,即 $ \lambda =\dfrac{1}{2} $ , $ \mu =\dfrac{1}{4} $ ,故 $ \lambda +\mu =\dfrac{3}{4} $ .
8.如图,在 $ △ABC $ 中,点 $ D $ 是 $ BC $ 的中点,点 $ E $ 在边 $ AC $ 上,且满足 $ 3\overrightarrow {AE}=\overrightarrow {AC} $ , $ BE $ 交 $ AD $ 于点 $ F $ ,设 $ \overrightarrow {BF}=\lambda \overrightarrow {AB}+\mu \overrightarrow {AC}(\lambda ,\mu \in \boldsymbol{R}) $ ,则 $ \lambda +\mu = $ ( )

A. $ -1 $
B. $ -\dfrac{1}{2} $
C. $ \dfrac{1}{2} $
D.1
答案:B
解析:设 $ \overrightarrow {AF}=m\overrightarrow {AD}(0 < m < 1) $ ,因为 $ B $ , $ F $ , $ E $ 三点共线,所以可设 $ \overrightarrow {AF}=k\overrightarrow {AE}+(1-k)\overrightarrow {AB} $ ,
又 $ 3\overrightarrow {AE}=\overrightarrow {AC} $ ,所以 $ \overrightarrow {AF}=\dfrac{k}{3}\overrightarrow {AC}+(1-k)\overrightarrow {AB} $ .
又因为 $ \overrightarrow {AD}=\dfrac{1}{2}(\overrightarrow {AB}+\overrightarrow {AC})=\dfrac{1}{m}\overrightarrow {AF} $ ,
所以 $ \overrightarrow {AF}=\dfrac{k}{3}\overrightarrow {AC}+(1-k)\overrightarrow {AB}=\dfrac{m}{2}(\overrightarrow {AB}+\overrightarrow {AC})=\dfrac{m}{2}\overrightarrow {AB}+\dfrac{m}{2}\overrightarrow {AC} $ ,
所以 $ \begin{cases}\dfrac{k}{3}=\dfrac{m}{2},\\ 1-k=\dfrac{m}{2},\end{cases} $ 解得 $ \begin{cases}m=\dfrac{1}{2},\\ k=\dfrac{3}{4},\end{cases} $
所以 $ \overrightarrow {AF}=\dfrac{1}{4}\overrightarrow {AC}+\dfrac{1}{4}\overrightarrow {AB} $ ,所以 $ \overrightarrow {BF}=\overrightarrow {AF}-\overrightarrow {AB}=\dfrac{1}{4}\overrightarrow {AC}-\dfrac{3}{4}\overrightarrow {AB} $ .
又 $ \overrightarrow {BF}=\lambda \overrightarrow {AB}+\mu \overrightarrow {AC} $ ,所以 $ \lambda =-\dfrac{3}{4} $ , $ \mu =\dfrac{1}{4} $ ,则 $ \lambda +\mu =-\dfrac{1}{2} $ .故选 $ \mathrm{B} $ .
二、刷提升
1.若 $ \boldsymbol{a} $ , $ \boldsymbol{b} $ 是平面内一组不共线的非零向量,则下列四组向量也可以作为一个基底的为( )
$ ①\boldsymbol{a}-\boldsymbol{b} $ 和 $ 2025\boldsymbol{b}-2025\boldsymbol{a} $ ; $ ②\boldsymbol{a}+\boldsymbol{b} $ 和 $ \boldsymbol{a}-\boldsymbol{b} $ ;
$ ③3\boldsymbol{a}-2\boldsymbol{b} $ 和 $ 2\boldsymbol{a}-3\boldsymbol{b} $ ; $ ④\boldsymbol{a}-3\boldsymbol{b} $ 和 $ 6\boldsymbol{b}-2\boldsymbol{a} $ .
A.①②
B.②③
C.③④
D.①④
答案:B
解析:对于①,因为 $ 2025\boldsymbol{b}-2025\boldsymbol{a}=-2025(\boldsymbol{a}-\boldsymbol{b}) $ ,所以 $ \boldsymbol{a}-\boldsymbol{b} $ 和 $ 2025\boldsymbol{b}-2025\boldsymbol{a} $ 是共线向量,不能作为一个基底;
对于②,设 $ \boldsymbol{a}+\boldsymbol{b}=\lambda (\boldsymbol{a}-\boldsymbol{b}) $ ,可得 $ \begin{cases}\lambda =1,\\ \lambda =-1,\end{cases} $ 方程组无解,所以 $ \boldsymbol{a}+\boldsymbol{b} $ 和 $ \boldsymbol{a}-\boldsymbol{b} $ 不共线,可以作为一个基底;
对于③,设 $ 3\boldsymbol{a}-2\boldsymbol{b}=\mu (2\boldsymbol{a}-3\boldsymbol{b}) $ ,可得 $ \begin{cases}2\mu =3,\\ -3\mu =-2,\end{cases} $ 方程组无解,所以 $ 3\boldsymbol{a}-2\boldsymbol{b} $ 和 $ 2\boldsymbol{a}-3\boldsymbol{b} $ 不共线,可以作为一个基底;
对于④,因为 $ \boldsymbol{a}-3\boldsymbol{b}=-\dfrac{1}{2}(6\boldsymbol{b}-2\boldsymbol{a}) $ ,所以 $ \boldsymbol{a}-3\boldsymbol{b} $ 和 $ 6\boldsymbol{b}-2\boldsymbol{a} $ 是共线向量,不能作为一个基底.故选 $ \mathrm{B} $ .
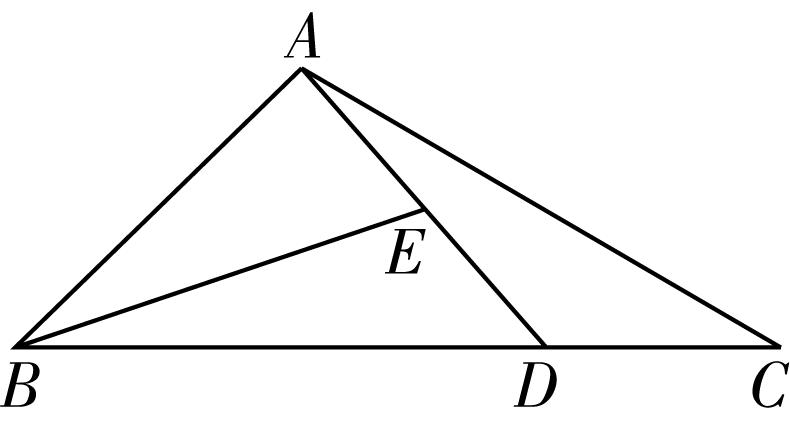
2.如图,在 $ △ABC $ 中, $ \overrightarrow {BD}=2\overrightarrow {DC} $ ,点 $ E $ 是线段 $ AD $ 的中点,则 $ \overrightarrow {AC}= $ ( )
A. $ \dfrac{3}{4}\overrightarrow {AD}+\dfrac{1}{2}\overrightarrow {BE} $
B. $ \dfrac{3}{4}\overrightarrow {AD}+\overrightarrow {BE} $
C. $ \dfrac{5}{4}\overrightarrow {AD}+\dfrac{1}{2}\overrightarrow {BE} $
D. $ \dfrac{5}{4}\overrightarrow {AD}+\overrightarrow {BE} $
答案:C
解析:由题意知, $ \overrightarrow {AC}=\overrightarrow {AD}+\overrightarrow {DC}=\overrightarrow {AD}+\dfrac{1}{2}\overrightarrow {BD}=\overrightarrow {AD}+\dfrac{1}{2}(\overrightarrow {BE}+\overrightarrow {ED})=\overrightarrow {AD}+\dfrac{1}{2}\overrightarrow {BE}+\dfrac{1}{2}\overrightarrow {ED}=\overrightarrow {AD}+\dfrac{1}{2}\overrightarrow {BE}+\dfrac{1}{2}\cdot \dfrac{1}{2}\overrightarrow {AD}=\dfrac{5}{4}\overrightarrow {AD}+\dfrac{1}{2}\overrightarrow {BE} $ .故选 $ \mathrm{C} $ .

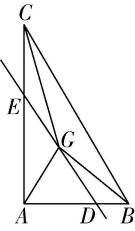
3.(多选)如图,已知 $ △ABC $ , $ AB=1 $ , $ AC=\sqrt{3} $ , $ BC=2 $ ,其内有一点 $ G $ ,满足 $ \overrightarrow {GA}+\overrightarrow {GB}+\overrightarrow {GC}=0 $ ,过点 $ G $ 的直线分别交 $ AB $ , $ AC $ 于点 $ D $ , $ E $ .设 $ \overrightarrow {AD}=\lambda \overrightarrow {AB} $ , $ \overrightarrow {AE}=\mu \overrightarrow {AC}(0 < \lambda < 1,0 < \mu < 1) $ ,则下列说法正确的是( )
 (多选)
(多选)
A. $ \overrightarrow {AG}=\dfrac{1}{3}\overrightarrow {AB}+\dfrac{1}{4}\overrightarrow {AC} $
B.点 $ G $ 为 $ △ABC $ 的重心
C. $ \dfrac{1}{\lambda }+\dfrac{1}{\mu }=3 $
D. $ |\overrightarrow {CG}|=\dfrac{\sqrt{13}}{3} $
答案:BCD
解析:对于 $ \mathrm{A} $ :由 $ \overrightarrow {GA}+\overrightarrow {GB}+\overrightarrow {GC}=0 $ 得 $ \overrightarrow {GA}+(\overrightarrow {AG}+\overrightarrow {GB})+(\overrightarrow {AG}+\overrightarrow {GC})=2\overrightarrow {AG}⇒\overrightarrow {AB}+\overrightarrow {AC}=3\overrightarrow {AG}⇒\overrightarrow {AG}=\dfrac{1}{3}\overrightarrow {AB}+\dfrac{1}{3}\overrightarrow {AC} $ ,故 $ \mathrm{A} $ 错误;
对于 $ \mathrm{B} $ :如图,取 $ BC $ 的中点为 $ M $ ,连接 $ GM $ ,由 $ \overrightarrow {GA}+\overrightarrow {GB}+\overrightarrow {GC}=0 $ 得 $ \overrightarrow {GA}=-(\overrightarrow {GB}+\overrightarrow {GC})=-2\overrightarrow {GM} $ ,所以点 $ A $ , $ G $ , $ M $ 共线,且 $ G $ 为靠近点 $ M $ 的三等分点,即 $ G $ 为 $ △ABC $ 的重心,故 $ \mathrm{B} $ 正确;
对于 $ \mathrm{C} $ :由 $ \overrightarrow {AG}=\dfrac{1}{3}\overrightarrow {AB}+\dfrac{1}{3}\overrightarrow {AC}=\dfrac{1}{3\lambda }\overrightarrow {AD}+\dfrac{1}{3\mu }\overrightarrow {AE} $ , $ D $ , $ G $ , $ E $ 三点共线,得 $ \dfrac{1}{3\lambda }+\dfrac{1}{3\mu }=1⇒\dfrac{1}{\lambda }+\dfrac{1}{\mu }=3 $ ,故 $ \mathrm{C} $ 正确;
对于 $ \mathrm{D} $ :因为 $ AC=\sqrt{3} $ , $ BC=2 $ , $ AB=1 $ ,所以 $ A{C}^{2}+A{B}^{2}=B{C}^{2} $ ,所以 $ AB\perp AC $ ,
设 $ AB $ 的中点为 $ N $ ,连接 $ GN $ ,由 $ G $ 为 $ △ABC $ 的重心,可知 $ C $ , $ G $ , $ N $ 三点共线,则 $ AN=\dfrac{1}{2}AB=\dfrac{1}{2} $ ,在 $ \mathrm{R}\mathrm{t}△ACN $ 中,有 $ CN=\sqrt{A{C}^{2}+A{N}^{2}}=\dfrac{\sqrt{13}}{2} $ ,又 $ G $ 为重心,所以 $ CG=\dfrac{2}{3}CN=\dfrac{\sqrt{13}}{3} $ ,故 $ \mathrm{D} $ 正确.故选 $ \mathrm{B}\mathrm{C}\mathrm{D} $ .
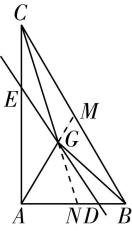
4.(多选)已知等边三角形 $ ABC $ 的边长为 $ {\rm 2,} \overrightarrow {BD}=2\overrightarrow {DC} $ , $ \overrightarrow {CE}=2\overrightarrow {EA} $ , $ AD $ 交 $ BE $ 于点 $ M $ ,则( )(多选)
A. $ \overrightarrow {AD}=\dfrac{1}{3}\overrightarrow {AB}+\dfrac{2}{3}\overrightarrow {AC} $
B. $ \overrightarrow {BM}=\dfrac{3}{4}\overrightarrow {BE} $
C. $ {S}_{△BMD}=8{S}_{△AME} $
D. $ {S}_{四边形CDME}=\dfrac{3\sqrt{3}}{7} $
答案:AC
解析:对于 $ \mathrm{A} $ ,因为 $ \overrightarrow {BD}=2\overrightarrow {DC} $ ,所以 $ \overrightarrow {BD}=\dfrac{2}{3}\overrightarrow {BC} $ ,所以 $ \overrightarrow {AD}=\overrightarrow {AB}+\overrightarrow {BD}=\overrightarrow {AB}+\dfrac{2}{3}\overrightarrow {BC}=\overrightarrow {AB}+\dfrac{2}{3}(\overrightarrow {AC}-\overrightarrow {AB})=\dfrac{1}{3}\overrightarrow {AB}+\dfrac{2}{3}\overrightarrow {AC} $ ,故 $ \mathrm{A} $ 正确;
对于 $ \mathrm{B} $ ,设 $ \overrightarrow {BM}=k\overrightarrow {BE}(k\in \boldsymbol{R}) $ ,所以 $ \overrightarrow {AM}=\overrightarrow {AB}+\overrightarrow {BM}=\overrightarrow {AB}+k\overrightarrow {BE}=\overrightarrow {AB}+k(\dfrac{1}{3}\overrightarrow {AC}-\overrightarrow {AB})=(1-k)\overrightarrow {AB}+\dfrac{1}{3}k\overrightarrow {AC} $ ,
又 $ A $ , $ M $ , $ D $ 三点在一条直线上,故 $ \overrightarrow {AM}//\overrightarrow {AD} $ ,故 $ \dfrac{1-k}{\dfrac{1}{3}}=\dfrac{\dfrac{1}{3}k}{\dfrac{2}{3}} $ ,解得 $ k=\dfrac{6}{7} $ ,即 $ \overrightarrow {BM}=\dfrac{6}{7}\overrightarrow {BE} $ ,
故 $ \mathrm{B} $ 错误;

对于 $ \mathrm{C} $ ,设 $ {S}_{△AME}=S $ ,由于 $ \overrightarrow {BM}=\dfrac{6}{7}\overrightarrow {BE} $ ,则
$ {S}_{△ABE}=7{S}_{△AME}=7S $ , $ {S}_{△ABM}=6{S}_{△AME}=6S $ ,
又 $ \overrightarrow {AM}=\dfrac{1}{7}\overrightarrow {AB}+\dfrac{2}{7}\overrightarrow {AC}=\dfrac{3}{7}\overrightarrow {AD} $ ,所以 $ {S}_{△ABM}=\dfrac{3}{7}{S}_{△ABD}⇒{S}_{△ABD}=14S⇒{S}_{△BMD}=8S $ ,故 $ \mathrm{C} $ 正确;
对于 $ \mathrm{D} $ ,因为 $ \overrightarrow {CE}=2\overrightarrow {EA} $ ,所以 $ {S}_{△BEC}=2{S}_{△ABE}=14S $ ,所以 $ {S}_{四边形CDME}={S}_{△BEC}-{S}_{△BMD}=14S-8S=6S $ ,
由 $ {S}_{△ABC}={S}_{△ABE}+{S}_{△BEC}=21S=\dfrac{\sqrt{3}}{4}×{2}^{2} $ ,得 $ S=\dfrac{\sqrt{3}}{21} $ ,所以 $ {S}_{四边形CDME}=6S=\dfrac{2\sqrt{3}}{7} $ ,故 $ \mathrm{D} $ 错误.
故选 $ \mathrm{A}\mathrm{C} $ .
5.在等腰梯形 $ ABCD $ 中,已知 $ AB//DC $ , $ AB=2 $ , $ BC=1 $ , $ \mathrm{\angle }DAB={60}^{\circ } $ ,点 $ P $ 在线段 $ BC $ 上,且 $ \overrightarrow {AP}=m\overrightarrow {AB}+n\overrightarrow {AD}(m,n\in \boldsymbol{R}) $ ,当点 $ P $ 为线段 $ BC $ 中点时, $ m+n= $ ;当点 $ P $ 在线段 $ BC $ 上运动时, $ m+n $ 的最大值为 .
答案: $ \dfrac{5}{4} $ ; $ \dfrac{3}{2} $
解析:如图,连接 $ AC $ .
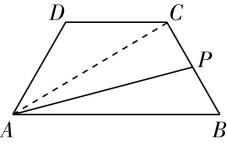
因为 $ AB=2 $ , $ BC=1 $ , $ \mathrm{\angle }DAB={60}^{\circ } $ ,
所以 $ DC=AB-2AD \cos {60}^{\circ }=2-1=1 $ ,故 $ \overrightarrow {DC}=\dfrac{1}{2}\overrightarrow {AB} $ .
当点 $ P $ 为线段 $ BC $ 中点时, $ \overrightarrow {AP}=\dfrac{1}{2}(\overrightarrow {AB}+\overrightarrow {AC})=\dfrac{1}{2}(\overrightarrow {AB}+\overrightarrow {AD}+\dfrac{1}{2}\overrightarrow {AB})=\dfrac{3}{4}\overrightarrow {AB}+\dfrac{1}{2}\overrightarrow {AD} $ ,
又 $ \overrightarrow {AP}=m\overrightarrow {AB}+n\overrightarrow {AD} $ ,所以 $ m=\dfrac{3}{4} $ , $ n=\dfrac{1}{2} $ ,所以 $ m+n=\dfrac{5}{4} $ .
当点 $ P $ 在线段 $ BC $ 上运动时, $ \overrightarrow {AP}=m\overrightarrow {AB}+n\overrightarrow {AD}=m\overrightarrow {AB}+n(\overrightarrow {AC}-\overrightarrow {DC})=m\overrightarrow {AB}+n(\overrightarrow {AC}-\dfrac{1}{2}\overrightarrow {AB})=(m-\dfrac{1}{2}n)\overrightarrow {AB}+n\overrightarrow {AC} $ ,
由 $ B $ , $ P $ , $ C $ 三点共线可知, $ m-\dfrac{1}{2}n+n=1 $ ,即 $ m+\dfrac{n}{2}=1 $ ,所以 $ m+n=1+\dfrac{n}{2} $ ,
又 $ \overrightarrow {AP}=(1-n)\overrightarrow {AB}+n\overrightarrow {AC} $ ,即 $ \overrightarrow {AP}-\overrightarrow {AB}=n(\overrightarrow {AC}-\overrightarrow {AB}) $ ,所以 $ \overrightarrow {BP}=n\overrightarrow {BC} $ ,所以 $ 0\leqslant n\leqslant 1 $ ,所以 $ m+n=1+\dfrac{n}{2}\leqslant \dfrac{3}{2} $ ,即 $ m+n $ 的最大值为 $ \dfrac{3}{2} $ .
6.如图,在平行四边形 $ ABCD $ 中, $ \overrightarrow {BE}=\dfrac{1}{2}\overrightarrow {BC} $ , $ \overrightarrow {CF}=2\overrightarrow {FD} $ .
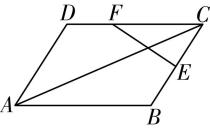
(1) 若 $ \overrightarrow {EF}=x\overrightarrow {AB}+y\overrightarrow {AD} $ ,求 $ 3x+2y $ 的值;
(2) 若 $ |\overrightarrow {AB}|=6 $ , $ |\overrightarrow {AD}|=4 $ , $ \mathrm{\angle }BAD={60}^{\circ } $ ,求 $ \overrightarrow {AC}\cdot \overrightarrow {EF} $ 的值.
答案:(1) 【解】 $ \because \overrightarrow {BE}=\dfrac{1}{2}\overrightarrow {BC} $ , $ \overrightarrow {CF}=2\overrightarrow {FD} $ , $ \therefore \overrightarrow {EF}=\overrightarrow {EC}+\overrightarrow {CF}=\dfrac{1}{2}\overrightarrow {BC}-\dfrac{2}{3}\overrightarrow {DC}=\dfrac{1}{2}\overrightarrow {AD}-\dfrac{2}{3}\overrightarrow {AB} $ .
又 $ \overrightarrow {EF}=x\overrightarrow {AB}+y\overrightarrow {AD} $ , $ \therefore x=-\dfrac{2}{3} $ , $ y=\dfrac{1}{2} $ ,故 $ 3x+2y=3×(-\dfrac{2}{3})+2×\dfrac{1}{2}=-1 $ .
(2) $ \because \overrightarrow {AC}=\overrightarrow {AB}+\overrightarrow {AD} $ , $ \therefore \overrightarrow {AC}\cdot \overrightarrow {EF}=(\overrightarrow {AB}+\overrightarrow {AD})\cdot (\dfrac{1}{2}\overrightarrow {AD}-\dfrac{2}{3}\overrightarrow {AB})=\dfrac{1}{2}{\overrightarrow {AD}}^{2}-\dfrac{2}{3}{\overrightarrow {AB}}^{2}-\dfrac{1}{6}\overrightarrow {AB}\cdot \overrightarrow {AD} $ .
又 $ \because |\overrightarrow {AB}|=6 $ , $ |\overrightarrow {AD}|=4 $ , $ \mathrm{\angle }BAD={60}^{\circ } $ ,
$ \therefore \overrightarrow {AC}\cdot \overrightarrow {EF}=\dfrac{1}{2}×16-\dfrac{2}{3}×36-\dfrac{1}{6}×6×4× \cos {60}^{\circ }=8-24-2=-18 $ ,
故 $ \overrightarrow {AC}\cdot \overrightarrow {EF} $ 的值为 $ -18 $ .
解析:
7.如图,在 $ △ABC $ 中, $ D $ 是 $ BC $ 的中点, $ E $ 在边 $ AB $ 上且 $ BE=2EA $ , $ AD $ 与 $ CE $ 交于点 $ O $ .
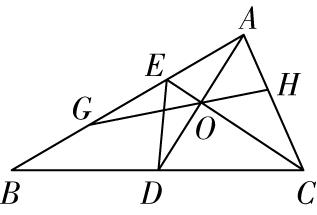
(1) 用 $ \overrightarrow {AB} $ , $ \overrightarrow {AC} $ 表示 $ \overrightarrow {DE} $ ;
(2) 过点 $ O $ 作直线交线段 $ AB $ 于点 $ G $ ,交线段 $ AC $ 于点 $ H $ ,且 $ \overrightarrow {AG}=\dfrac{2}{3}\overrightarrow {AB} $ , $ \overrightarrow {AH}=t\overrightarrow {AC} $ ,求 $ t $ 的值.
答案:(1) 【解】 $ \overrightarrow {DE}=\overrightarrow {AE}-\overrightarrow {AD}=\dfrac{1}{3}\overrightarrow {AB}-\dfrac{1}{2}(\overrightarrow {AB}+\overrightarrow {AC})=-\dfrac{1}{6}\overrightarrow {AB}-\dfrac{1}{2}\overrightarrow {AC} $ .
(2) 因为 $ E $ , $ C $ , $ O $ 三点共线,设 $ \overrightarrow {EO}=\lambda \overrightarrow {EC}(\lambda \in \boldsymbol{R}) $ ,所以 $ \overrightarrow {AO}-\overrightarrow {AE}=\lambda (\overrightarrow {AC}-\overrightarrow {AE}) $ , $ \overrightarrow {AO}=\lambda \overrightarrow {AC}+(1-\lambda )\overrightarrow {AE} $ .
由 $ BE=2EA $ 得 $ \overrightarrow {AO}=\lambda \overrightarrow {AC}+(1-\lambda )\dfrac{1}{3}\overrightarrow {AB} $ .
设 $ \overrightarrow {AO}=\mu \overrightarrow {AD}(\mu \in \boldsymbol{R}) $ ,所以 $ \overrightarrow {AO}=\dfrac{\mu }{2}\overrightarrow {AB}+\dfrac{\mu }{2}\overrightarrow {AC} $ ,
则有 $ \begin{cases}\lambda =\dfrac{\mu }{2},\\ \dfrac{1-\lambda }{3}=\dfrac{\mu }{2},\end{cases} $ 解得 $ \lambda =\dfrac{1}{4} $ ,即 $ \overrightarrow {AO}=\dfrac{1}{4}\overrightarrow {AC}+\dfrac{1}{4}\overrightarrow {AB} $ .
又 $ G $ , $ O $ , $ H $ 三点共线,设 $ \overrightarrow {AO}=m\overrightarrow {AG}+(1-m)\overrightarrow {AH}(m\in \boldsymbol{R}) $ ,又 $ \overrightarrow {AO}=m\cdot \dfrac{2}{3}\overrightarrow {AB}+(1-m)\cdot t\overrightarrow {AC} $ ,
所以 $ \begin{cases}\dfrac{2m}{3}=\dfrac{1}{4},\\ (1-m)t=\dfrac{1}{4},\end{cases} $ 解得 $ \begin{cases}m=\dfrac{3}{8},\\ t=\dfrac{2}{5}.\end{cases} $
解析:









 (多选)
(多选)



