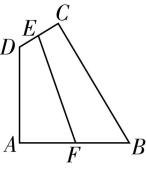
5.如图,在四边形 $ ABCD $ 中, $ AB\perp AD $ , $ CD\perp CB $ , $ \mathrm{\angle }ABC={60}^{\circ } $ , $ AB=2 $ , $ AD=\sqrt{3} $ , $ E $ 为线段 $ CD $ 的中点, $ F $ 为线段 $ AB $ 上一动点(包括端点),且 $ \overrightarrow {EF}=\lambda \overrightarrow {DA}+\mu \overrightarrow {CB} $ ,则下列说法错误的是( )
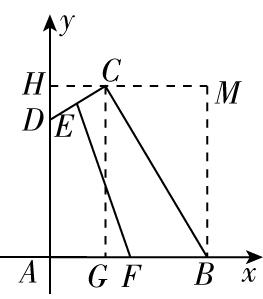
解析:以 $ A $ 为坐标原点, $ AB $ 所在直线为 $ x $ 轴, $ AD $ 所在直线为 $ y $ 轴,建立如图所示的平面直角坐标系,过点 $ C $ 作 $ CG\perp x $ 轴于点 $ G $ ,作 $ CH\perp y $ 轴于点 $ H $ ,过点 $ B $ 作 $ BM\perp CH $ 交 $ HC $ 的延长线于点 $ M $ ,则 $ △CDH\sim △BCM $ .
因为 $ AB\perp AD $ , $ CD\perp CB $ , $ \mathrm{\angle }ABC={60}^{\circ } $ ,所以 $ \mathrm{\angle }CDH={60}^{\circ } $ ,设 $ HD=x $ ,则 $ CH=\sqrt{3}x $ , $ BM=AH=\sqrt{3}+x $ , $ CM=HM-CH=AB-CH=2-\sqrt{3}x $ ,则 $ \dfrac{HD}{MC}=\dfrac{CH}{BM} $ ,即 $ \dfrac{x}{2-\sqrt{3}x}=\dfrac{\sqrt{3}x}{\sqrt{3}+x} $ ,解得 $ x=\dfrac{\sqrt{3}}{4} $ 或 $ x=0 $ (舍去).
则 $ A(0,0) $ , $ B(2,0) $ , $ D(0,\sqrt{3}) $ , $ C(\dfrac{3}{4},\dfrac{5\sqrt{3}}{4}) $ , $ E(\dfrac{3}{8},\dfrac{9\sqrt{3}}{8}) $ ,
则 $ BC=\sqrt{B{M}^{2}+C{M}^{2}}=\sqrt{\dfrac{75}{16}+\dfrac{25}{16}}=\dfrac{5}{2} $ ,
$ \mathrm{A} $ 正确;
若 $ F $ 为线段 $ AB $ 的中点,则 $ F(1,0) $ ,
所以 $ \overrightarrow {EF}=(\dfrac{5}{8},-\dfrac{9\sqrt{3}}{8}) $ , $ \overrightarrow {DA}=(0,-\sqrt{3}) $ , $ \overrightarrow {CB}=(\dfrac{5}{4},-\dfrac{5\sqrt{3}}{4}) $ ,又 $ \overrightarrow {EF}=\lambda \overrightarrow {DA}+\mu \overrightarrow {CB} $ ,
所以 $ \begin{cases}\dfrac{5}{8}=\dfrac{5}{4}\mu ,\\ -\dfrac{9\sqrt{3}}{8}=-\sqrt{3}\lambda -\dfrac{5\sqrt{3}}{4}\mu ,\end{cases} $ 解得 $ \begin{cases}\lambda =\dfrac{1}{2},\\ \mu =\dfrac{1}{2},\end{cases} $
则 $ \lambda +\mu =1 $ , $ \mathrm{B} $ 正确;
设 $ F(m,0) $ , $ 0\leqslant m\leqslant 2 $ ,则 $ \overrightarrow {FC}\cdot \overrightarrow {FD}=(\dfrac{3}{4}-m,\dfrac{5\sqrt{3}}{4})\cdot (-m,\sqrt{3})={m}^{2}-\dfrac{3}{4}m+\dfrac{15}{4}={\left(m-\dfrac{3}{8}\right) ^ {2}}+\dfrac{231}{64} $ ,故当 $ m=\dfrac{3}{8} $ 时, $ \overrightarrow {FC}\cdot \overrightarrow {FD} $ 取得最小值,且最小值为 $ \dfrac{231}{64} $ ,
$ \mathrm{C} $ 错误;
$ \overrightarrow {EF}=(m-\dfrac{3}{8},-\dfrac{9\sqrt{3}}{8}) $ ,又 $ \overrightarrow {EF}=\lambda \overrightarrow {DA}+\mu \overrightarrow {CB} $ ,
所以 $ \begin{cases}m-\dfrac{3}{8}=\dfrac{5}{4}\mu ,\\ -\dfrac{9\sqrt{3}}{8}=-\sqrt{3}\lambda -\dfrac{5\sqrt{3}}{4}\mu ,\end{cases} $
因为 $ 0\leqslant m\leqslant 2 $ ,所以 $ m-\dfrac{3}{8}\in [-\dfrac{3}{8},\dfrac{13}{8}] $ ,即 $ \dfrac{5}{4}\mu \in [-\dfrac{3}{8},\dfrac{13}{8}] $ ,所以 $ \mu \in [-\dfrac{3}{10} $ , $ \dfrac{13}{10} ] $ , $ \dfrac{13}{10}-(-\dfrac{3}{10})=\dfrac{8}{5} $ ,所以 $ \mu $ 的最大值比最小值大 $ \dfrac{8}{5} $ , $ \mathrm{D} $ 正确.故选 $ \mathrm{C} $ .