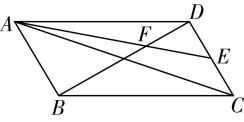
2.如图,在四边形 $ ABCD $ 中, $ \overrightarrow {AB}+\overrightarrow {AD}=\overrightarrow {AC} $ , $ |\overrightarrow {AD}|=2|\overrightarrow {AB}|=2 $ , $ \overrightarrow {AB}\cdot \overrightarrow {AD}=1 $ , $ E $ 为 $ CD $ 的中点, $ AE $ 与 $ DB $ 相交于点 $ F $ ,则下列说法一定正确的是( )
 (多选)
(多选)
A. $ \overrightarrow {AF}=\dfrac{1}{3}\overrightarrow {AB}+\dfrac{2}{3}\overrightarrow {AD} $
B. $ \overrightarrow {BF} $ 在 $ \overrightarrow {AB} $ 上的投影向量为 $ 0 $
C. $ \overrightarrow {AF}\cdot \overrightarrow {AB}=1 $
D.若 $ \alpha =\dfrac{1}{2}\mathrm{\angle }DEF $ ,则 $ \mathrm{ \tan }\alpha =\dfrac{\sqrt{3}}{3} $
在四边形 $ ABCD $ 中,因为 $ \overrightarrow {AB}+\overrightarrow {AD}=\overrightarrow {AC} $ ,所以四边形 $ ABCD $ 为平行四边形.
又 $ |\overrightarrow {AD}|=2|\overrightarrow {AB}|=2 $ , $ \overrightarrow {AB}\cdot \overrightarrow {AD}=1 $ ,所以 $ \mathrm{\angle }BAD={60}^{\circ } $ .
对于 $ \mathrm{A} $ , $ \overrightarrow {AE}=\overrightarrow {AD}+\overrightarrow {DE}=\overrightarrow {AD}+\dfrac{1}{2}\overrightarrow {AB} $ ,设 $ \overrightarrow {AF}=\lambda \overrightarrow {AE}=\lambda (\overrightarrow {AD}+\dfrac{1}{2}\overrightarrow {AB})=\lambda \overrightarrow {AD}+\dfrac{1}{2}\lambda \overrightarrow {AB} $ .
因为 $ B $ , $ F $ , $ D $ 三点共线,所以 $ \lambda +\dfrac{1}{2}\lambda =1 $ ,解得 $ \lambda =\dfrac{2}{3} $ ,所以 $ \overrightarrow {AF}=\dfrac{1}{3}\overrightarrow {AB}+\dfrac{2}{3}\overrightarrow {AD} $ ,故选项 $ \mathrm{A} $ 正确.
对于 $ \mathrm{B} $ ,设 $ \overrightarrow {BF} $ 与 $ \overrightarrow {AB} $ 的夹角为 $ \theta $ .因为 $ \overrightarrow {BD}=\overrightarrow {AD}-\overrightarrow {AB} $ ,所以 $ {\overrightarrow {BD}}^{2}=(\overrightarrow {AD}-\overrightarrow {AB})^{2}={\overrightarrow {AD}}^{2}+{\overrightarrow {AB}}^{2}-2\overrightarrow {AD}\cdot \overrightarrow {AB}=3 $ ,所以 $ BD=|\overrightarrow {BD}|=\sqrt{3} $ .在 $ △ABD $ 中,因为 $ AB=1 $ , $ AD=2 $ , $ BD=\sqrt{3} $ ,所以 $ A{D}^{2}=A{B}^{2}+B{D}^{2} $ ,所以 $ BD\perp AB $ ,即 $ \theta ={90}^{\circ } $ ,所以 $ \overrightarrow {BF} $ 在 $ \overrightarrow {AB} $ 上的投影向量为 $ |\overrightarrow {BF}| \cos \theta \cdot \dfrac{\overrightarrow {AB}}{|\overrightarrow {AB}|}=0×\dfrac{\overrightarrow {AB}}{|\overrightarrow {AB}|}=0 $ ,故选项 $ \mathrm{B} $ 正确.
对于 $ \mathrm{C} $ ,由题意, $ \overrightarrow {AF}\cdot \overrightarrow {AB}=(\dfrac{1}{3}\overrightarrow {AB}+\dfrac{2}{3}\overrightarrow {AD})\cdot \overrightarrow {AB}=\dfrac{1}{3}{\overrightarrow {AB}}^{2}+\dfrac{2}{3}\overrightarrow {AB}\cdot \overrightarrow {AD}=\dfrac{1}{3}+\dfrac{2}{3}×1=1 $ ,故选项 $ \mathrm{C} $ 正确.
对于 $ \mathrm{D} $ , $ |\overrightarrow {AF}|=\sqrt{\dfrac{1}{9}{\overrightarrow {AB}}^{2}+\dfrac{4}{9}{\overrightarrow {AD}}^{2}+\dfrac{4}{9}\overrightarrow {AB}\cdot \overrightarrow {AD}}=\dfrac{\sqrt{21}}{3} $ ,则 $ \cos \mathrm{\angle }FAB=\dfrac{\overrightarrow {AF}\cdot \overrightarrow {AB}}{|\overrightarrow {AF}||\overrightarrow {AB}|}=\dfrac{1}{\dfrac{\sqrt{21}}{3}}=\dfrac{\sqrt{21}}{7} $ .若 $ \tan \alpha =\dfrac{\sqrt{3}}{3} $ ,则结合题意知 $ \alpha ={30}^{\circ } $ ,又因为 $ \alpha =\dfrac{1}{2}\mathrm{\angle }DEF=\dfrac{1}{2}\mathrm{\angle }FAB={30}^{\circ } $ ,所以 $ \mathrm{\angle }FAB=2\alpha ={60}^{\circ } $ ,不满足 $ \cos \mathrm{\angle }FAB=\dfrac{\sqrt{21}}{7} $ ,故选项 $ \mathrm{D} $ 不正确.故选 $ \mathrm{A}\mathrm{B}\mathrm{C} $ .