专题2 向量与三角形形状的判定、奔驰定理与四心

由题意得, $ |\overrightarrow {BC}|=|\overrightarrow {AB}+\overrightarrow {AC}|⇒|\overrightarrow {AB}-\overrightarrow {AC}|=|\overrightarrow {AB}+\overrightarrow {AC}| $ ,故 $ {\overrightarrow {AB}}^{2}-2\overrightarrow {AB}\cdot \overrightarrow {AC}+{\overrightarrow {AC}}^{2}={\overrightarrow {AB}}^{2}+2\overrightarrow {AB}\cdot \overrightarrow {AC}+{\overrightarrow {AC}}^{2} $ ,则 $ \overrightarrow {AB}\cdot \overrightarrow {AC}=0 $ ,故 $ \overrightarrow {AB}\perp \overrightarrow {AC} $ ,即 $ △ABC $ 为直角三角形.故选 $ \mathrm{D} $ .

因为 $ \overrightarrow {BA}\cdot \overrightarrow {AC}+{\overrightarrow {AC}}^{2}=0 $ ,即 $ (\overrightarrow {BA}+\overrightarrow {AC})\cdot \overrightarrow {AC}=0 $ ,即 $ \overrightarrow {BC}\cdot \overrightarrow {AC}=0 $ ,

所以 $ \overrightarrow {BC}\perp \overrightarrow {AC} $ ,即 $ AC\perp BC $ ,所以 $ \mathrm{\angle }ACB=\dfrac{\mathrm{\pi }}{2} $ .又 $ \dfrac{\overrightarrow {AC}}{|\overrightarrow {AC}|} $ 表示与 $ \overrightarrow {AC} $ 同向的单位向量, $ \dfrac{\overrightarrow {AB}}{|\overrightarrow {AB}|} $ 表示与 $ \overrightarrow {AB} $ 同向的单位向量,

所以 $ \dfrac{\overrightarrow {AC}}{|\overrightarrow {AC}|}\cdot \dfrac{\overrightarrow {AB}}{|\overrightarrow {AB}|}=1×1× \cos \mathrm{\angle }CAB=\dfrac{\sqrt{2}}{2} $ .又 $ \mathrm{\angle }CAB\in (0,\dfrac{\mathrm{\pi }}{2}) $ ,所以 $ \mathrm{\angle }CAB=\dfrac{\mathrm{\pi }}{4} $ ,

所以 $ \mathrm{\angle }CBA=\dfrac{\mathrm{\pi }}{4} $ ,所以 $ △ABC $ 是等腰直角三角形．故选 $ \mathrm{A} $ .

$ \because \overrightarrow {AB} $ , $ \overrightarrow {AC} $ 是非零向量且满足 $ (\overrightarrow {AB}-2\overrightarrow {AC})\perp \overrightarrow {AB} $ , $ (\overrightarrow {AC}-2\overrightarrow {AB})\perp \overrightarrow {AC} $ ,

$ \therefore (\overrightarrow {AB}-2\overrightarrow {AC})\cdot \overrightarrow {AB}=(\overrightarrow {AC}-2\overrightarrow {AB})\cdot \overrightarrow {AC}=0 $ ,

$ \therefore |\overrightarrow {AB}{|}^{2}=|\overrightarrow {AC}{|}^{2}=2|\overrightarrow {AB}||\overrightarrow {AC}|\cdot \cos \mathrm{\angle }BAC $ , $ \therefore |\overrightarrow {AB}|=|\overrightarrow {AC}| $ , $ \mathrm{\angle }BAC={60}^{\circ } $ .

$ \therefore △ABC $ 是等边三角形,故选 $ \mathrm{B} $ .

设 $ \overrightarrow {BD}=t\overrightarrow {BC}(t\ne 1) $ ,则 $ \overrightarrow {BA}-t\overrightarrow {BC}=\overrightarrow {BA}-\overrightarrow {BD}=\overrightarrow {DA} $ ,

所以 $ |\overrightarrow {BA}-t\overrightarrow {BC}| > |\overrightarrow {AC}| $ 即为 $ |\overrightarrow {DA}| > |\overrightarrow {AC}| $ ,

所以 $ AC $ 是边 $ BC $ 上的高,即 $ CA\perp CB $ ,即 $ C=\dfrac{\mathrm{\pi }}{2} $ ,故 $ △ABC $ 为直角三角形,故充分性成立.

若 $ △ABC $ 为直角三角形,不一定有 $ C=\dfrac{\mathrm{\pi }}{2} $ ,故不一定有对于任意 $ t\ne 1 $ , $ |\overrightarrow {BA}-t\overrightarrow {BC}| > |\overrightarrow {AC}| $ ,故必要性不成立.所以“对于任意 $ t\ne 1 $ , $ |\overrightarrow {BA}-t\overrightarrow {BC}| > |\overrightarrow {AC}| $ ”是“ $ △ABC $ 为直角三角形”的充分不必要条件.故选 $ \mathrm{A} $ .

对于 $ \mathrm{A} $ ,如图,根据向量加法的平行四边形法则,可得 $ \overrightarrow {AB}+\overrightarrow {AC}=\overrightarrow {AE} $ ,若 $ \overrightarrow {AM}=\dfrac{1}{2}\overrightarrow {AB}+\dfrac{1}{2}\overrightarrow {AC}=\dfrac{1}{2}\overrightarrow {AE} $ ,则 $ M $ 是边 $ AE $ 的中点,由四边形 $ ABEC $ 为平行四边形,可知 $ M $ 是边 $ BC $ 的中点,故 $ \mathrm{A} $ 正确；

对于 $ \mathrm{B} $ ,若 $ MA=MB=MC $ ,则 $ M $ 是 $ △ABC $ 的外心,故 $ \mathrm{B} $ 错误；

对于 $ \mathrm{C} $ ,若 $ \overrightarrow {AM}=-\overrightarrow {BM}-\overrightarrow {CM} $ ,则 $ \overrightarrow {AM}+\overrightarrow {BM}+\overrightarrow {CM}=0 $ ,即 $ \overrightarrow {MA}+\overrightarrow {MB}+\overrightarrow {MC}=0 $ ,所以 $ M $ 是 $ △ABC $ 的重心,故 $ \mathrm{C} $ 正确；

对于 $ \mathrm{D} $ ,因为 $ \dfrac{\overrightarrow {AB}}{|\overrightarrow {AB}|} $ 表示与 $ \overrightarrow {AB} $ 同向的单位向量, $ \dfrac{\overrightarrow {AC}}{|\overrightarrow {AC}|} $ 表示与 $ \overrightarrow {AC} $ 同向的单位向量,

所以 $ \dfrac{\overrightarrow {AB}}{|\overrightarrow {AB}|}+\dfrac{\overrightarrow {AC}}{|\overrightarrow {AC}|} $ 与 $ \mathrm{\angle }BAC $ 的平分线同向,

又 $ \overrightarrow {AM}=\lambda (\dfrac{\overrightarrow {AB}}{|\overrightarrow {AB}|}+\dfrac{\overrightarrow {AC}}{|\overrightarrow {AC}|}) $ ,则 $ M $ 在 $ \mathrm{\angle }BAC $ 的平分线上,则动点 $ M $ 的轨迹过 $ △ABC $ 的内心,故 $ \mathrm{D} $ 正确.

故选 $ \mathrm{A}\mathrm{C}\mathrm{D} $ .

因为 $ |\overrightarrow {OA}|=|\overrightarrow {OB}|=|\overrightarrow {OC}| $ ，所以 $ O $ 到点 $ A $ , $ B $ , $ C $ 的距离相等，所以 $ O $ 为 $ △ABC $ 的外心.

由 $ \overrightarrow {NA}+\overrightarrow {NB}+\overrightarrow {NC}=0 $ ，得 $ \overrightarrow {NA}+\overrightarrow {NB}=-\overrightarrow {NC} $ ，

如图，取 $ AB $ 的中点 $ E $ ，连接 $ NE $ ，则 $ \overrightarrow {NA}+\overrightarrow {NB}=2\overrightarrow {NE}=\overrightarrow {CN} $ ，所以 $ 2|\overrightarrow {NE}|=|\overrightarrow {CN}| $ ，所以 $ N $ 是 $ △ABC $ 的重心.

由 $ \overrightarrow {PA}\cdot \overrightarrow {PB}=\overrightarrow {PB}\cdot \overrightarrow {PC}=\overrightarrow {PC}\cdot \overrightarrow {PA} $ ，得 $ (\overrightarrow {PA}-\overrightarrow {PC})\cdot \overrightarrow {PB}=0 $ ，即 $ \overrightarrow {CA}\cdot \overrightarrow {PB}=0 $ ，所以 $ AC\perp PB $ ，同理 $ AB\perp PC $ ，所以点 $ P $ 为 $ △ABC $ 的垂心．故选 $ \mathrm{C} $ ．

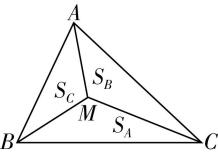
$ \mathrm{A} $ 选项,因为 $ {S}_{A}:{S}_{B}:{S}_{C}=1:1:1 $ ,所以 $ \overrightarrow {MA}+\overrightarrow {MB}+\overrightarrow {MC}=0 $ ,

如图①,取 $ BC $ 的中点 $ D $ ,连接 $ MD $ ,则 $ \overrightarrow {MB}+\overrightarrow {MC}=2\overrightarrow {MD} $ ,所以 $ 2\overrightarrow {MD}=-\overrightarrow {MA} $ ,所以 $ A $ , $ M $ , $ D $ 三点共线,且 $ MA=2MD $ ,

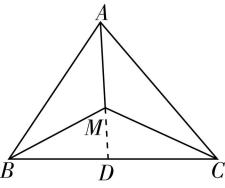
图①

所以 $ M $ 为 $ △ABC $ 的重心, $ \mathrm{A} $ 正确.

$ \mathrm{B} $ 选项,若 $ M $ 为 $ △ABC $ 的内心,可设内切圆半径为 $ r $ ,则 $ {S}_{A}=\dfrac{1}{2}BC\cdot r $ , $ {S}_{B}=\dfrac{1}{2}AC\cdot r $ , $ {S}_{C}=\dfrac{1}{2}AB\cdot r $ ,所以 $ \dfrac{1}{2}BC\cdot r\cdot \overrightarrow {MA}+\dfrac{1}{2}AC\cdot r\cdot \overrightarrow {MB}+\dfrac{1}{2}AB\cdot r\cdot \overrightarrow {MC}=0 $ ,即 $ BC\cdot \overrightarrow {MA}+AC\cdot \overrightarrow {MB}+AB\cdot \overrightarrow {MC}=0 $ , $ \mathrm{B} $ 正确.

$ \mathrm{C} $ 选项,若 $ M $ 为 $ △ABC $ 的垂心, $ 3\overrightarrow {MA}+4\overrightarrow {MB}+5\overrightarrow {MC}=0 $ ,则 $ {S}_{A}:{S}_{B}:{S}_{C}=3:4:5 $ ,

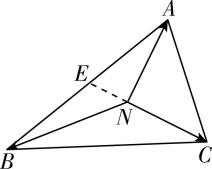
如图②, $ AD\perp BC $ , $ CE\perp AB $ , $ BF\perp AC $ , $ AD $ , $ CE $ , $ BF $ 相交于一点 $ M $ ,

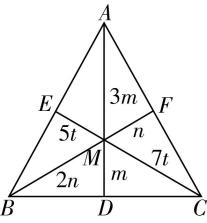
图②

又 $ {S}_{△ABC}={S}_{A}+{S}_{B}+{S}_{C} $ ,

则 $ \dfrac{{S}_{A}}{{S}_{△ABC}}=\dfrac{3}{12}=\dfrac{1}{4} $ ,即 $ AM:MD=3:1 $ ,

$ \dfrac{{S}_{B}}{{S}_{△ABC}}=\dfrac{4}{12}=\dfrac{1}{3} $ ,即 $ MF:BM=1:2 $ ,

$ \dfrac{{S}_{C}}{{S}_{△ABC}}=\dfrac{5}{12} $ ,即 $ ME:MC=5:7 $ ,

设 $ MD=m $ , $ MF=n $ , $ ME=5t $ ,则 $ AM=3m $ , $ BM=2n $ , $ MC=7t $ ,

因为 $ \mathrm{\angle }CAD=\mathrm{\angle }CBF $ , $ \sin \mathrm{\angle }CAD=\dfrac{n}{3m} $ , $ \sin \mathrm{\angle }CBF=\dfrac{m}{2n} $ ,所以 $ \dfrac{n}{3m}=\dfrac{m}{2n} $ ,即 $ m=\dfrac{\sqrt{6}}{3}n $ ,

同理可得 $ \dfrac{m}{7t}=\dfrac{5t}{3m} $ ,即 $ m=\dfrac{\sqrt{105}}{3}t $ ,故 $ n=\dfrac{\sqrt{70}}{2}t $ .

又 $ \cos \mathrm{\angle }BMD=\dfrac{m}{2n}=\dfrac{\dfrac{\sqrt{6}}{3}n}{2n}=\dfrac{\sqrt{6}}{6} $ ,则 $ \sin \mathrm{\angle }BMD=\sqrt{1-{\left(\dfrac{\sqrt{6}}{6}\right) ^ {2}}}=\dfrac{\sqrt{30}}{6} $ ,

故 $ BD=BM \sin \mathrm{\angle }BMD=2n\cdot \dfrac{\sqrt{30}}{6}=\dfrac{\sqrt{30}}{3}n $ ,

又 $ \cos \mathrm{\angle }CMD=\dfrac{m}{7t}=\dfrac{\dfrac{\sqrt{105}}{3}t}{7t}=\dfrac{\sqrt{105}}{21} $ ,则 $ \sin \mathrm{\angle }CMD=\sqrt{1-{\left(\dfrac{\sqrt{105}}{21}\right) ^ {2}}}=\dfrac{4\sqrt{21}}{21} $ ,

故 $ CD=MC \sin \mathrm{\angle }CMD=7t\cdot \dfrac{4\sqrt{21}}{21}=\dfrac{4\sqrt{21}}{3}t $ .

因为 $ \tan \mathrm{\angle }ABC=\dfrac{AD}{BD} $ , $ \tan \mathrm{\angle }BCA=\dfrac{AD}{CD} $ ,

所以 $ \tan \mathrm{\angle }ABC: \tan \mathrm{\angle }BCA=\dfrac{AD}{BD}\cdot \dfrac{CD}{AD}=\dfrac{CD}{BD}=\dfrac{\dfrac{4\sqrt{21}}{3}t}{\dfrac{\sqrt{30}}{3}n}=\dfrac{4\sqrt{21}t}{\sqrt{30}n}=\dfrac{4\sqrt{21}t}{\sqrt{30}\cdot \dfrac{\sqrt{70}}{2}t}=\dfrac{4}{5} $ ,

同理可得 $ \tan \mathrm{\angle }BAC: \tan \mathrm{\angle }ABC=\dfrac{3}{4} $ ,

故 $ \tan \mathrm{\angle }BAC: \tan \mathrm{\angle }ABC: \tan \mathrm{\angle }BCA=3:4:5 $ , $ \mathrm{C} $ 正确.

$ \mathrm{D} $ 选项,若 $ \mathrm{\angle }BAC={45}^{\circ } $ , $ \mathrm{\angle }ABC={60}^{\circ } $ , $ M $ 为 $ △ABC $ 的外心,则 $ \mathrm{\angle }ACB={75}^{\circ } $ ,

设 $ △ABC $ 的外接圆半径为 $ R $ ,则 $ \mathrm{\angle }BMC=2\mathrm{\angle }BAC={90}^{\circ } $ , $ \mathrm{\angle }AMC=2\mathrm{\angle }ABC={120}^{\circ } $ ,

$ \mathrm{\angle }AMB=2\mathrm{\angle }ACB={150}^{\circ } $ ,则 $ {S}_{A}=\dfrac{1}{2}{R}^{2} $ ,如图③,过点 $ A $ 作 $ MC $ 边的高,得 $ {ℎ}_{B}=AM\cdot \sin {60}^{\circ }=\dfrac{\sqrt{3}}{2}R $ ,则 $ {S}_{B}=\dfrac{\sqrt{3}}{4}{R}^{2} $ ,过点 $ A $ 作 $ BM $ 边上的高,则 $ {ℎ}_{C}=AM\cdot \sin {30}^{\circ }=\dfrac{1}{2}R $ ,故 $ {S}_{C}=\dfrac{1}{4}{R}^{2} $ ,所以 $ {S}_{A}:{S}_{B}:{S}_{C}=2:\sqrt{3}:1 $ , $ \mathrm{D} $ 错误 .

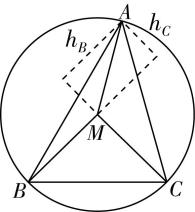
图③

故选 $ \mathrm{A}\mathrm{B}\mathrm{C} $ .

如图,取 $ D $ , $ E $ 分别为 $ BC $ , $ AC $ 的中点,连接 $ OD $ , $ OE $ ,由 $ \overrightarrow {OA}+2\overrightarrow {OB}+3\overrightarrow {OC}=0 $ 得 $ \overrightarrow {OA}+\overrightarrow {OC}=-2(\overrightarrow {OB}+\overrightarrow {OC}) $ ,即 $ \overrightarrow {OE}=-2\overrightarrow {OD} $ ,所以 $ O $ , $ D $ , $ E $ 三点共线,且 $ OE=2OD $ .

$ {S}_{△COE}={S}_{△AOE} $ , $ {S}_{△COD}={S}_{△BOD} $ ,

设 $ {S}_{△AOC}={S}_{1} $ , $ {S}_{△BOC}={S}_{2} $ ,则 $ {S}_{△COE}={S}_{△AOE}=\dfrac{{S}_{1}}{2} $ , $ {S}_{△COD}={S}_{△BOD}=\dfrac{{S}_{2}}{2} $ .

因为 $ D $ , $ E $ 分别为 $ BC $ , $ AC $ 的中点,所以 $ DE//AB $ , $ DE=\dfrac{1}{2}AB $ ,

所以 $ \dfrac{{S}_{△CDE}}{{S}_{△ABC}}=\dfrac{1}{4} $ ,所以 $ \dfrac{{S}_{△CDE}}{{S}_{四边形ABDE}}=\dfrac{1}{3} $ ,即 $ \dfrac{\dfrac{{S}_{1}}{2}+\dfrac{{S}_{2}}{2}}{\dfrac{{S}_{1}}{2}+\dfrac{{S}_{2}}{2}+{S}_{△OAB}}=\dfrac{1}{3} $ ,解得 $ {S}_{1}+{S}_{2}={S}_{△OAB} $ ,

因为 $ {S}_{△AOE}:{S}_{△BOD}=2:1 $ ,所以 $ {S}_{1}:{S}_{2}=2:1 $ ,即 $ {S}_{2}=\dfrac{{S}_{1}}{2} $ ,所以 $ {S}_{1}+\dfrac{{S}_{1}}{2}={S}_{△OAB} $ ,所以 $ {S}_{1}=\dfrac{2}{3}{S}_{△OAB} $ ,即 $ △OAC $ 的面积与 $ △OAB $ 的面积之比是 $ \dfrac{2}{3} $ ,故选 $ \mathrm{B} $ .