6.4.1 平面几何中的向量方法+6.4.2 向量在物理中的应用举例

1．（多选）已知 $ △ABC $ 是边长为3的等边三角形，点 $ P $ 在 $ △ABC $ 内（包括边界），则下列说法正确的是（）（多选）

A． $ \overrightarrow {AB}\cdot \overrightarrow {BC}=\dfrac{9}{2} $

B．若 $ \overrightarrow {BP}=\dfrac{1}{2}\overrightarrow {PC} $ ，则 $ |\overrightarrow {AP}|=\sqrt{7} $

C．若 $ |\overrightarrow {AP}|=2 $ ，则点 $ P $ 的轨迹长度为 $ \dfrac{2\mathrm{\pi }}{3} $

D．若 $ |\overrightarrow {AP}|=|\overrightarrow {BP}|=\sqrt{3} $ ，则 $ |\overrightarrow {CP}|=\sqrt{3} $

答案：BCD

解析：

对于 $ \mathrm{A} $ 选项, $ \overrightarrow {AB}\cdot \overrightarrow {BC}=-\overrightarrow {BA}\cdot \overrightarrow {BC}=-|\overrightarrow {BA}|\cdot |\overrightarrow {BC}| \cos \dfrac{\mathrm{\pi }}{3}=-{3}^{2}×\dfrac{1}{2}=-\dfrac{9}{2} $ , $ \mathrm{A} $ 错误；

对于 $ \mathrm{B} $ 选项,若 $ \overrightarrow {BP}=\dfrac{1}{2}\overrightarrow {PC} $ ,则 $ \overrightarrow {AP}-\overrightarrow {AB}=\dfrac{1}{2}(\overrightarrow {AC}-\overrightarrow {AP}) $ ,所以 $ 3\overrightarrow {AP}=2\overrightarrow {AB}+\overrightarrow {AC} $ ,

故 $ 9{\overrightarrow {AP}}^{2}={\left(2\overrightarrow {AB}+\overrightarrow {AC}\right) ^ {2}}=4{\overrightarrow {AB}}^{2}+4\overrightarrow {AB}\cdot \overrightarrow {AC}+{\overrightarrow {AC}}^{2}=4{|\overrightarrow {AB}|}^{2}+4|\overrightarrow {AB}|\cdot |\overrightarrow {AC}| \cos \dfrac{\mathrm{\pi }}{3}+{|\overrightarrow {AC}|}^{2}= $

$ 4×{3}^{2}+4×{3}^{2}×\dfrac{1}{2}+{3}^{2}=63 $ ,故 $ |\overrightarrow {AP}|=\sqrt{7} $ , $ \mathrm{B} $ 正确；

对于 $ \mathrm{C} $ 选项, $ |\overrightarrow {AP}|=2 $ ,则点 $ P $ 的轨迹是半径为2,圆心角为 $ A=\dfrac{\mathrm{\pi }}{3} $ 的圆弧,

故点 $ P $ 的轨迹长度为 $ \dfrac{\mathrm{\pi }}{3}×2=\dfrac{2\mathrm{\pi }}{3} $ , $ \mathrm{C} $ 正确；

对于 $ \mathrm{D} $ 选项,因为 $ |\overrightarrow {AP}|=|\overrightarrow {BP}|=\sqrt{3} $ , $ |\overrightarrow {AB}|=3 $ ,所以 $ {|\overrightarrow {AP}|}^{2}={|\overrightarrow {BP}-\overrightarrow {BA}|}^{2}={\overrightarrow {BP}}^{2}-2\overrightarrow {BA}\cdot \overrightarrow {BP}+{\overrightarrow {BA}}^{2}={|\overrightarrow {BP}|}^{2}-2|\overrightarrow {BA}|\cdot |\overrightarrow {BP}| \cos \mathrm{\angle }ABP+{|\overrightarrow {BA}|}^{2}=3-2×3×\sqrt{3} \cos \mathrm{\angle }ABP+9=3 $ ,解得 $ \cos \mathrm{\angle }ABP=\dfrac{\sqrt{3}}{2} $ ,

因为 $ 0\leqslant \mathrm{\angle }ABP\leqslant \mathrm{\pi } $ ,所以 $ \mathrm{\angle }ABP=\dfrac{\mathrm{\pi }}{6} $ ,所以 $ \mathrm{\angle }CAP=\mathrm{\angle }CBP=\dfrac{\mathrm{\pi }}{3}-\mathrm{\angle }ABP=\dfrac{\mathrm{\pi }}{6} $ ,

所以 $ |\overrightarrow {CP}|=|\overrightarrow {AP}-\overrightarrow {AC}|=\sqrt{{\left(\overrightarrow {AP}-\overrightarrow {AC}\right) ^ {2}}}=\sqrt{{\overrightarrow {AP}}^{2}-2\overrightarrow {AP}\cdot \overrightarrow {AC}+{\overrightarrow {AC}}^{2}} $

$ =\sqrt{3-2\sqrt{3}×3×\dfrac{\sqrt{3}}{2}+9}=\sqrt{3} $ , $ \mathrm{D} $ 正确.

故选 $ \mathrm{B}\mathrm{C}\mathrm{D} $ .

2．如图，在 $ △ABC $ 中， $ \mathrm{\angle }BAC={120}^{\circ } $ ， $ AB=AC=3 $ ，点 $ D $ 在线段 $ BC $ 上，且 $ BD=\dfrac{1}{2}DC $ .求：

试题资源网 https://stzy.com

（1） $ AD $ 的长等于；

（2） $ \mathrm{\angle }DAC $ 的大小为 .

答案：

（1） $ \sqrt{3} $

（2） $ {90}^{\circ } $

解析：

（1）设 $ \overrightarrow {AB}=\boldsymbol{a} $ , $ \overrightarrow {AC}=\boldsymbol{b} $ ,则 $ \overrightarrow {AD}=\overrightarrow {AB}+\overrightarrow {BD}=\overrightarrow {AB}+\dfrac{1}{3}\overrightarrow {BC}=\overrightarrow {AB}+\dfrac{1}{3}(\overrightarrow {AC}-\overrightarrow {AB})=\dfrac{2}{3}\overrightarrow {AB}+\dfrac{1}{3}\overrightarrow {AC}=\dfrac{2}{3}\boldsymbol{a}+\dfrac{1}{3}\boldsymbol{b} $ .

$ \therefore |\overrightarrow {AD}{|}^{2}={\left(\dfrac{2}{3}\boldsymbol{a}+\dfrac{1}{3}\boldsymbol{b}\right) ^ {2}}=\dfrac{4}{9}{\boldsymbol{a}}^{2}+2×\dfrac{2}{9}\boldsymbol{a}\cdot \boldsymbol{b}+\dfrac{1}{9}{\boldsymbol{b}}^{2}=\dfrac{4}{9}×9+2×\dfrac{2}{9}×3×3× \cos {120}^{\circ }+\dfrac{1}{9}×9=3 $ , $ \therefore AD=\sqrt{3} $ .

（2）设 $ \mathrm{\angle }DAC=\theta ({0}^{\circ } < \theta < {120}^{\circ }) $ ,则 $ \theta $ 为 $ \overrightarrow {AD} $ 与 $ \overrightarrow {AC} $ 的夹角.

$ \because \cos \theta =\dfrac{\overrightarrow {AD}\cdot \overrightarrow {AC}}{|\overrightarrow {AD}||\overrightarrow {AC}|}=\dfrac{(\dfrac{2}{3}\boldsymbol{a}+\dfrac{1}{3}\boldsymbol{b})\cdot \boldsymbol{b}}{\sqrt{3}×3}=\dfrac{\dfrac{2}{3}\boldsymbol{a}\cdot \boldsymbol{b}+\dfrac{1}{3}{\boldsymbol{b}}^{2}}{3\sqrt{3}}=\dfrac{\dfrac{2}{3}×3×3×(-\dfrac{1}{2})+\dfrac{1}{3}×9}{3\sqrt{3}}= $

$ {\rm 0,} \therefore \theta ={90}^{\circ } $ ,即 $ \mathrm{\angle }DAC={90}^{\circ } $ .

3．已知三个点 $ A(0,0) $ , $ B(1,2) $ , $ D(4,-2) $ .

（1）求证： $ AB\perp AD $ ；

（2）要使四边形 $ ABCD $ 为矩形，求点 $ C $ 的坐标并求矩形 $ ABCD $ 两条对角线所成的锐角的正切值.

答案：

（1）【证明】由 $ A(0,0) $ , $ B(1,2) $ , $ D(4,-2) $ ,得 $ \overrightarrow {AB}=(1,2) $ , $ \overrightarrow {AD}=(4,-2) $ ,

则 $ \overrightarrow {AB}\cdot \overrightarrow {AD}=1×4+2×(-2)=0 $ ,即 $ \overrightarrow {AB}\perp \overrightarrow {AD} $ ,则 $ AB\perp AD $ .

（2）【解】由（1）知 $ \overrightarrow {AB}\perp \overrightarrow {AD} $ , $ \because $ 四边形 $ ABCD $ 为矩形, $ \therefore \overrightarrow {DC}=\overrightarrow {AB} $ .

设点 $ C $ 坐标为 $ (x,y) $ ,则 $ \overrightarrow {AB}=(1,2) $ , $ \overrightarrow {DC}=(x-4,y+2) $ ,

$ \therefore \begin{cases}x-4=1,\\ y+2=2,\end{cases} $ 解得 $ \begin{cases}x=5,\\ y=0,\end{cases} $ 故点 $ C $ 的坐标为 $ (5,0) $ .

$ \because \overrightarrow {AC}=(5,0) $ , $ \overrightarrow {BD}=(3,-4) $ , $ \therefore \overrightarrow {AC}\cdot \overrightarrow {BD}=15+0=15 $ ， $ |\overrightarrow {AC}|=5 $ , $ |\overrightarrow {BD}|=5 $ .

设 $ \overrightarrow {AC} $ 与 $ \overrightarrow {BD} $ 的夹角为 $ \theta $ ,则 $ \cos \theta =\dfrac{\overrightarrow {AC}\cdot \overrightarrow {BD}}{|\overrightarrow {AC}||\overrightarrow {BD}|}=\dfrac{15}{25}=\dfrac{3}{5} $ ,

$ \therefore \sin \theta =\sqrt{1-{ \cos }^{2}\theta }=\dfrac{4}{5}⇒ \tan \theta =\dfrac{ \sin \theta }{ \cos \theta }=\dfrac{4}{3} $ ,

故矩形 $ ABCD $ 的两条对角线所成的锐角的正切值为 $ \dfrac{4}{3} $ .

解析：

5．若同一平面内的三个力 $ {F}_{1} $ , $ {F}_{2} $ , $ {F}_{3} $ 作用于同一个物体，且该物体处于平衡状态.已知 $ |{F}_{1}|=3 $ , $ |{F}_{2}|=4 $ ，且 $ {F}_{1} $ 与 $ {F}_{2} $ 的夹角为 $ {120}^{\circ } $ ，则力 $ {F}_{3} $ 的大小为（）

A．37

B． $ \sqrt{37} $

C．13

D． $ \sqrt{13} $

答案：D

解析：

由题意可知, $ {F}_{1}+{F}_{2}+{F}_{3}=0 $ ,所以 $ {F}_{3}=-({F}_{1}+{F}_{2}) $ ,

所以 $ {|{F}_{3}|}^{2}={F}_{3}^{2}=({F}_{1}+{F}_{2})^{2}={F}_{1}^{2}+2{F}_{1}\cdot {F}_{2}+{F}_{2}^{2}={3}^{2}+2×3×4× \cos {120}^{\circ }+{4}^{2}=13 $ ,

故 $ |{F}_{3}|=\sqrt{13} $ ,则力 $ {F}_{3} $ 的大小为 $ \sqrt{13} $ .故选 $ \mathrm{D} $ .

6．一条东西方向的河流两岸平行，河宽 $ 800\mathrm{m} $ ，水流的速度为向东 $ 4\mathrm{k}\mathrm{m}/\mathrm{h} $ .河南岸有一码头 $ A $ ，码头 $ A $ 正对面有一货站 $ B(AB $ 与河的方向垂直 $ ) $ ， $ B $ 的正西方向且与 $ B $ 相距 $ 600\mathrm{m} $ 另有货站 $ C $ ，已知一货船匀速航行，当货船自码头 $ A $ 航行到货站 $ C $ 航程最短时，合速度为 $ 5\mathrm{k}\mathrm{m}/\mathrm{h} $ .

（1）求货船航行速度的大小；

（2）若货船从 $ A $ 出发垂直到达正对岸的货站 $ B $ 处，求货船到达 $ B $ 处所需时间.

答案：

（1）【解】以 $ A $ 为坐标原点,以东向为 $ x $ 轴正方向,以北向为 $ y $ 轴正方向建立平面直角坐标系如图所示,

货船从码头 $ A $ 航行到货站 $ C $ 的最短路径要求合速度方向由 $ A $ 指向 $ C $ ,

设货船在静水中的速度为 $ \overrightarrow {AQ}=(x,y) $ ,水流速度为向东 $ 4\mathrm{k}\mathrm{m}/\mathrm{h} $ ,即 $ \overrightarrow {AP}=(4,0) $ ,

合速度为水流速度与船速的和 $ \overrightarrow {AR}=\overrightarrow {AP}+\overrightarrow {AQ}=(x+4,y) $ .

由题意,合速度方向与向量 $ \overrightarrow {AC}=(-0.6,0.8) $ 同向,且大小为 $ 5\mathrm{k}\mathrm{m}/\mathrm{h} $ ,

设合速度 $ \overrightarrow {AR}=k(-0.6,0.8) $ ,则 $ \sqrt{(-0.6k)^{2}+(0.8k)^{2}}=5⇒k=5 $ .

因此合速度为 $ \overrightarrow {AR}=(-3,4) $ ,

则 $ \begin{cases}x+4=-3,\\ y=4\end{cases}⇒\begin{cases}x=-7,\\ y=4,\end{cases} $

故货船速度大小为 $ |\overrightarrow {AQ}|=\sqrt{(-7)^{2}+{4}^{2}}=\sqrt{65}\mathrm{k}\mathrm{m}/\mathrm{h} $ .

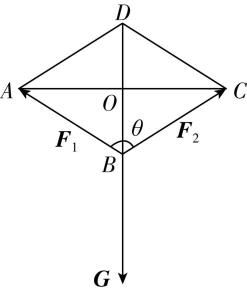
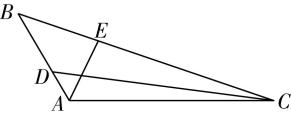
试题资源网 https://stzy.com

（2）货船要垂直到达正对岸 $ B $ 处,即货船的实际速度 $ \overrightarrow {AR\prime }=\overrightarrow {AQ\prime }+\overrightarrow {AP} $ ,且 $ \overrightarrow {AR\prime }\perp \overrightarrow {AP} $ ,

设 $ \overrightarrow {AQ\prime }=(x\prime ,y\prime ) $ , $ \overrightarrow {AP}=(4,0) $ ,则 $ \overrightarrow {AR\prime }=(x\prime +4,y\prime ) $ .

由 $ \overrightarrow {AR\prime }\cdot \overrightarrow {AP}=0 $ 得 $ x\prime +4=0 $ ,则 $ x\prime =-4 $ ,则 $ \overrightarrow {AQ\prime }=(-4,y\prime ) $ ,

由（1）知船速大小为 $ \sqrt{65}\mathrm{k}\mathrm{m}/\mathrm{h} $ ,

故 $ (-4)^{2}+y{\prime }^{2}=65⇒y\prime =7 $ ,

因为河宽 $ 0.8\mathrm{k}\mathrm{m} $ ,所以货船到达 $ B $ 处所需时间 $ t=\dfrac{0.8}{7}=\dfrac{4}{35}\mathrm{h} $ .

解析：

二、刷提升

1．如图，在 $ △ABC $ 中， $ AB=4 $ ， $ AC=3 $ ， $ \mathrm{\angle }BAC={60}^{\circ } $ ， $ D $ 是 $ BC $ 的中点， $ CE\perp AB $ ， $ AD $ 与 $ CE $ 交于点 $ F $ .则 $ \cos \mathrm{\angle }CFD= $ （）

试题资源网 https://stzy.com

A． $ \dfrac{2\sqrt{57}}{19} $

B． $ \dfrac{\sqrt{57}}{19} $

C． $ \dfrac{\sqrt{111}}{74} $

D． $ \dfrac{3\sqrt{111}}{74} $

答案：D

解析：

由 $ CE\perp AB $ ,得 $ CE=AC \sin \mathrm{\angle }BAC=3× \sin {60}^{\circ }=\dfrac{3\sqrt{3}}{2} $ ,且 $ AE=AC \cos \mathrm{\angle }BAC=3× \cos {60}^{\circ }=\dfrac{3}{2} $ ,则 $ \overrightarrow {AE}=\dfrac{3}{8}\overrightarrow {AB} $ ,又 $ D $ 是 $ BC $ 的中点,即 $ AD $ 是 $ △ABC $ 的中线,则 $ \overrightarrow {AD}=\dfrac{1}{2}(\overrightarrow {AB}+\overrightarrow {AC}) $ ,则 $ {\overrightarrow {AD}}^{2}=\dfrac{1}{4}({\overrightarrow {AB}}^{2}+2\overrightarrow {AB}\cdot \overrightarrow {AC}+{\overrightarrow {AC}}^{2})=\dfrac{1}{4}×({4}^{2}+2×4×3× \cos {60}^{\circ }+{3}^{2})=\dfrac{37}{4} $ ,得 $ AD=\dfrac{\sqrt{37}}{2} $ .

所以 $ \overrightarrow {AD}\cdot \overrightarrow {CE}=\dfrac{1}{2}(\overrightarrow {AB}+\overrightarrow {AC})(\overrightarrow {AE}-\overrightarrow {AC}) $

$ =\dfrac{1}{2}(\overrightarrow {AB}+\overrightarrow {AC})(\dfrac{3}{8}\overrightarrow {AB}-\overrightarrow {AC}) $

$ =\dfrac{1}{2}(-\dfrac{5}{8}\overrightarrow {AB}\cdot \overrightarrow {AC}+\dfrac{3}{8}{\overrightarrow {AB}}^{2}-{\overrightarrow {AC}}^{2}) $

$ =\dfrac{1}{2}×(-\dfrac{5}{8}×4×3× \cos {60}^{\circ }+\dfrac{3}{8}×{4}^{2}-{3}^{2}) $

$ =-\dfrac{27}{8} $ ,

所以 $ \cos \mathrm{\angle }CFD= \cos ⟨\overrightarrow {AD} $ , $ \overrightarrow {EC}⟩=\dfrac{\overrightarrow {AD}\cdot \overrightarrow {EC}}{|\overrightarrow {AD}||\overrightarrow {EC}|}=\dfrac{\dfrac{27}{8}}{\dfrac{\sqrt{37}}{2}×\dfrac{3\sqrt{3}}{2}}=\dfrac{3\sqrt{111}}{74} $ .故选 $ \mathrm{D} $ .

2．若 $ △ABC $ 所在的平面上存在一点 $ P $ ，使得 $ \overrightarrow {AP}=\lambda \overrightarrow {AB}+\mu \overrightarrow {AC}(\lambda ,\mu \in \boldsymbol{R}) $ ，则下列说法错误的是（）（多选）

A．若 $ \lambda +\mu =1 $ ，则点 $ P $ 的轨迹不可能经过 $ △ABC $ 的外心

B．若 $ \lambda +\mu =-2 $ ，则点 $ P $ 的轨迹不可能经过 $ △ABC $ 的垂心

C．若 $ \lambda +\mu =\dfrac{1}{2} $ ，则点 $ P $ 的轨迹可能经过 $ △ABC $ 的重心

D．若 $ \lambda =\mu $ ，则点 $ P $ 的轨迹可能经过 $ △ABC $ 的内心

答案：ABC

解析：

若 $ \lambda +\mu =1 $ ,根据向量共线的推论知 $ P $ , $ B $ , $ C $ 三点共线,即点 $ P $ 在直线 $ BC $ 上,

在 $ △ABC $ 中,当 $ \mathrm{\angle }BAC={90}^{\circ } $ 时, $ BC $ 的中点为 $ △ABC $ 的外心,故点 $ P $ 有可能为外心, $ \mathrm{A} $ 错误；

若 $ \lambda +\mu =-2 $ ,不妨取 $ \lambda =-1 $ , $ \mu =-1 $ ,

当 $ AB=AC $ , $ \mathrm{\angle }BAC={120}^{\circ } $ 时, $ \overrightarrow {AP}\cdot \overrightarrow {BC}=(-\overrightarrow {AB}-\overrightarrow {AC})\cdot (\overrightarrow {AC}-\overrightarrow {AB})={\overrightarrow {AB}}^{2}-{\overrightarrow {AC}}^{2}=0 $ ,同理 $ \overrightarrow {CP}\cdot \overrightarrow {AB}=0 $ , $ \overrightarrow {BP}\cdot \overrightarrow {AC}=0 $ ,

此时点 $ P $ 为 $ △ABC $ 的垂心, $ \mathrm{B} $ 错误；

若点 $ P $ 为 $ △ABC $ 的重心,则必有 $ \overrightarrow {AP}=\dfrac{2}{3}×\dfrac{1}{2}(\overrightarrow {AB}+\overrightarrow {AC})=\dfrac{1}{3}(\overrightarrow {AB}+\overrightarrow {AC}) $ ,此时 $ \lambda +\mu =\dfrac{2}{3} $ ,

$ \mathrm{C} $ 错误；

若 $ \lambda =\mu $ ,设 $ △ABC $ 为等边三角形,结合 $ \overrightarrow {AP}=\lambda \overrightarrow {AB}+\lambda \overrightarrow {AC}(\lambda \in \boldsymbol{R}) $ ,

则点 $ P $ 在 $ BC $ 边的中线上,也在 $ \mathrm{\angle }BAC $ 的平分线上,此时点 $ P $ 的轨迹可能经过 $ △ABC $ 的内心, $ \mathrm{D} $ 正确.故选 $ \mathrm{A}\mathrm{B}\mathrm{C} $ .

3．（多选）长江某处的南北两岸平行，江面宽度 $ d $ 为 $ 2\mathrm{k}\mathrm{m} $ ，一艘船从江南岸边的 $ A $ 处出发到江北岸.如图，已知船在静水中的速度 $ {\boldsymbol{v}}_{1} $ 的大小为 $ |{\boldsymbol{v}}_{1}|=10\mathrm{k}\mathrm{m}/\mathrm{h} $ ，水流方向自西向东，且速度 $ {\boldsymbol{v}}_{2} $ 的大小为 $ |{\boldsymbol{v}}_{2}|=6\mathrm{k}\mathrm{m}/\mathrm{h} $ .设 $ {\boldsymbol{v}}_{1} $ 和 $ {\boldsymbol{v}}_{2} $ 的夹角为 $ \theta (0 < \theta < \mathrm{\pi }) $ ，北岸的点 $ A^\prime $ 在 $ A $ 的正北方向，则（）

试题资源网 https://stzy.com （多选）

A．当船的航行距离最短时， $ \cos \theta =-\dfrac{2}{5} $

B．当船的航行时间最短时， $ \theta =\dfrac{\mathrm{\pi }}{2} $

C．当 $ \theta =\dfrac{2\mathrm{\pi }}{3} $ 时，船航行到达北岸的位置在 $ A^\prime $ 的左侧

D．当 $ \theta =\dfrac{2\mathrm{\pi }}{3} $ 时，船的航行距离为 $ \dfrac{4\sqrt{57}}{15}\mathrm{k}\mathrm{m} $

答案：BD

解析：

对于 $ \mathrm{A} $ ，当船的航行距离最短时， $ {\boldsymbol{v}}_{1}+{\boldsymbol{v}}_{2} $ 的方向与河岸垂直，则 $ \cos \theta =- \cos (\mathrm{\pi }-\theta )=-\dfrac{|{\boldsymbol{v}}_{2}|}{|{\boldsymbol{v}}_{1}|}=-\dfrac{6}{10}=-\dfrac{3}{5} $ ，故 $ \mathrm{A} $ 错误；

对于 $ \mathrm{B} $ ，船的航行时间为 $ t=\dfrac{d}{|{\boldsymbol{v}}_{1}| \sin \theta }=\dfrac{1}{5 \sin \theta }\mathrm{h} $ ，若船的航行时间最短，则 $ \sin \theta $ 最大，也就是说当且仅当 $ \theta =\dfrac{\mathrm{\pi }}{2} $ 时，船的航行时间最短，故 $ \mathrm{B} $ 正确；

对于 $ \mathrm{C} $ ，当 $ \theta =\dfrac{2\mathrm{\pi }}{3} $ 时，船水平方向的速度大小为 $ |{\boldsymbol{v}}_{1}| \cos (\mathrm{\pi }-\dfrac{2}{3}\mathrm{\pi })-|{\boldsymbol{v}}_{2}|=-1(\mathrm{k}\mathrm{m}/\mathrm{h}) $ ，方向水平向右，故最终到达北岸时船在点 $ A^\prime $ 的右侧，故 $ \mathrm{C} $ 错误；

对于 $ \mathrm{D} $ ，由题意设位移分量分别为 $ {\boldsymbol{s}}_{1}=t{\boldsymbol{v}}_{1} $ , $ {\boldsymbol{s}}_{2}=t{\boldsymbol{v}}_{2} $ ，位移为 $ \boldsymbol{s} $ ，

则 $ \boldsymbol{s}={\boldsymbol{s}}_{1}+{\boldsymbol{s}}_{2}=t({\boldsymbol{v}}_{1}+{\boldsymbol{v}}_{2}) $ ，其中 $ t=\dfrac{d}{|{\boldsymbol{v}}_{1}| \sin \theta }=\dfrac{1}{5 \sin \dfrac{2\mathrm{\pi }}{3}}=\dfrac{2\sqrt{3}}{15} $ ，

所以 $ |\boldsymbol{s}|=t|{\boldsymbol{v}}_{1}+{\boldsymbol{v}}_{2}|=t\sqrt{{\left({\boldsymbol{v}}_{1}+{\boldsymbol{v}}_{2}\right) ^ {2}}}=\dfrac{2\sqrt{3}}{15}×\sqrt{{10}^{2}+{6}^{2}+2×10×6×(-\dfrac{1}{2})}=\dfrac{4\sqrt{57}}{15}(\mathrm{k}\mathrm{m}) $ ，

故 $ \mathrm{D} $ 正确．故选 $ \mathrm{B}\mathrm{D} $ ．

4．（多选）在日常生活中，我们会看到这样的情境：两个人共提一个行李包.假设行李包所受重力为 $ G $ ，作用在行李包上的两个拉力分别为 $ {F}_{1} $ , $ {F}_{2} $ ，且 $ |{F}_{1}|=|{F}_{2}| $ , $ {F}_{1} $ 与 $ {F}_{2} $ 的夹角为 $ \theta $ ，则下列结论中正确的是（）（多选）

A． $ |{F}_{1}|=\dfrac{|G|}{2 \cos \dfrac{\theta }{2}} $

B． $ \theta $ 越小越费力， $ \theta $ 越大越省力

C．当 $ \theta =\dfrac{2\mathrm{\pi }}{3} $ 时， $ |{F}_{1}|=|G| $

D． $ \theta $ 的范围为 $ [0,\mathrm{\pi }] $

答案：AC

解析：

画出示意图如图，因为 $ |{F}_{1}|=|{F}_{2}| $ ，所以 $ |{F}_{1}| \cos $ $ \dfrac{\theta }{2}=\dfrac{1}{2}|G| $ ，即 $ |{F}_{1}|=\dfrac{|G|}{2 \cos \dfrac{\theta }{2}} $ ，故 $ \mathrm{A} $ 正确；

根据向量加法的平行四边形法则， $ \theta $ 越小越省力， $ \theta $ 越大越费力，故 $ \mathrm{B} $ 错误；

当 $ \theta =\dfrac{2\mathrm{\pi }}{3} $ 时， $ \mathrm{\angle }ABD=\dfrac{\mathrm{\pi }}{3} $ ，又 $ AB=AD $ ，所以 $ △ABD $ 为等边三角形，即 $ |{F}_{1}|=|G| $ ，故 $ \mathrm{C} $ 正确；

若 $ \theta =\mathrm{\pi } $ ，则 $ {F}_{1}+{F}_{2}=0 $ ，与 $ {F}_{1}+{F}_{2}=-G $ 矛盾，所以 $ \theta \ne \mathrm{\pi } $ ，故 $ \mathrm{D} $ 错误.故选 $ \mathrm{A}\mathrm{C} $ .

试题资源网 https://stzy.com

5．如图，在 $ △ABC $ 中， $ AB=2 $ ， $ AC=4 $ ， $ \mathrm{\angle }BAC={120}^{\circ } $ ， $ \overrightarrow {BD}=2\overrightarrow {DA} $ ， $ \overrightarrow {CE}=2\overrightarrow {EB} $ .

试题资源网 https://stzy.com

（1）求 $ \overrightarrow {AE}\cdot \overrightarrow {CD} $ 的值.

（2）线段 $ BC $ 上是否存在一点 $ P $ ，使得 $ CD\perp AP $ ?若存在，求 $ \dfrac{CP}{CB} $ 的值；若不存在，说明理由.

（3）若 $ O $ 是 $ △ABC $ 内一点，且满足 $ \overrightarrow {OC}+2\overrightarrow {OB}+m\overrightarrow {OA}=0(m\in \boldsymbol{R}) $ ，求 $ \overrightarrow {OA}\cdot \overrightarrow {OC}+2\overrightarrow {OA}\cdot \overrightarrow {OB} $ 的最小值.

答案：

（1）【解】由题知 $ \overrightarrow {AE}=\overrightarrow {AB}+\overrightarrow {BE}=\overrightarrow {AB}+\dfrac{1}{3}\overrightarrow {BC}=\overrightarrow {AB}+\dfrac{1}{3}(\overrightarrow {AC}-A\overrightarrow {B})=\dfrac{2}{3}\overrightarrow {AB}+\dfrac{1}{3}\overrightarrow {AC} $ ,

$ \overrightarrow {CD}=\overrightarrow {AD}-\overrightarrow {AC}=\dfrac{1}{3}\overrightarrow {AB}-\overrightarrow {AC} $ .

$ \therefore \overrightarrow {AE}\cdot \overrightarrow {CD}=(\dfrac{2}{3}\overrightarrow {AB}+\dfrac{1}{3}\overrightarrow {AC})\cdot (\dfrac{1}{3}\overrightarrow {AB}-\overrightarrow {AC})=\dfrac{2}{9}{\overrightarrow {AB}}^{2}-\dfrac{5}{9}\overrightarrow {AB}\cdot \overrightarrow {AC}-\dfrac{1}{3}{\overrightarrow {AC}}^{2}=\dfrac{2}{9}×4+\dfrac{5}{9}×2×4×\dfrac{1}{2}-\dfrac{16}{3}=-\dfrac{20}{9} $ .

（2）设 $ \overrightarrow {CP}=\lambda \overrightarrow {CB}(0\leqslant \lambda \leqslant 1) $ ,

$ \because \overrightarrow {AP}=\overrightarrow {AC}+\overrightarrow {CP} $ ,

$ \therefore \overrightarrow {AP}=\overrightarrow {AC}+\lambda \overrightarrow {CB}=\overrightarrow {AC}+\lambda (\overrightarrow {AB}-\overrightarrow {AC})=\lambda \overrightarrow {AB}+(1-\lambda )\overrightarrow {AC} $ .

$ \because CD\perp AP $ , $ \therefore \overrightarrow {CD}\cdot \overrightarrow {AP}=0 $ ,

$ \therefore (\dfrac{1}{3}\overrightarrow {AB}-\overrightarrow {AC})\cdot [\lambda \overrightarrow {AB}+(1-\lambda )\overrightarrow {AC}]=\dfrac{1}{3}\lambda {\overrightarrow {AB}}^{2}-(1-\lambda ){\overrightarrow {AC}}^{2}+(\dfrac{1}{3}-\dfrac{4}{3}\lambda )\overrightarrow {AB}\cdot \overrightarrow {AC}=\dfrac{4}{3}\lambda -16+16\lambda -\dfrac{4}{3}+\dfrac{16}{3}\lambda =0 $ ,解得 $ \lambda =\dfrac{13}{17} $ ,

$ \therefore $ 存在一点 $ P $ ,使得 $ CD\perp AP $ ,此时 $ \dfrac{CP}{CB}=\dfrac{13}{17} $ .

（3） $ \because \overrightarrow {AE}=\dfrac{2}{3}\overrightarrow {AB}+\dfrac{1}{3}\overrightarrow {AC} $ ,

$ \therefore {\overrightarrow {AE}}^{2}=\dfrac{4}{9}{\overrightarrow {AB}}^{2}+\dfrac{1}{9}{\overrightarrow {AC}}^{2}+2×\dfrac{2}{3}×\dfrac{1}{3}×\overrightarrow {AB}\cdot \overrightarrow {AC}=\dfrac{16}{9}+\dfrac{16}{9}-2×\dfrac{2}{9}×4×2×\dfrac{1}{2}=\dfrac{16}{9} $ ,

$ \therefore |\overrightarrow {AE}|=\dfrac{4}{3} $ .

$ \because \overrightarrow {OC}+2\overrightarrow {OB}+m\overrightarrow {OA}=0(m\in \boldsymbol{R}) $ ,

$ \therefore \overrightarrow {OE}+\overrightarrow {EC}+2(\overrightarrow {OE}+\overrightarrow {EB})+m\overrightarrow {OA}=0 $ ,

$ \therefore 3\overrightarrow {OE}+m\overrightarrow {OA}=0 $ , $ \therefore m\overrightarrow {OA}=-3\overrightarrow {OE} $ , $ \therefore O $ , $ A $ , $ E $ 三点共线,又 $ O $ 在 $ △ABC $ 内, $ \therefore O $ 在线段 $ AE $ 上,

$ \therefore -m|\overrightarrow {OA}{|}^{2}=3\overrightarrow {OE}\cdot \overrightarrow {OA}=-3|\overrightarrow {OE}|\cdot |\overrightarrow {OA}|\geqslant -3\cdot {\left(\dfrac{|\overrightarrow {OE}|+|\overrightarrow {OA}|}{2}\right) ^ {2}}=-3×{\left(\dfrac{2}{3}\right) ^ {2}}=-\dfrac{4}{3} $ ,

当且仅当 $ |\overrightarrow {OE}|=|\overrightarrow {OA}|=\dfrac{2}{3} $ 时,即 $ O $ 为 $ AE $ 的中点时,等号成立,

而 $ \overrightarrow {OA}\cdot \overrightarrow {OC}+2\overrightarrow {OA}\cdot \overrightarrow {OB}=\overrightarrow {OA}\cdot (\overrightarrow {OC}+2\overrightarrow {OB})=-m{\overrightarrow {OA}}^{2} $ ,

故 $ \overrightarrow {OA}\cdot \overrightarrow {OC}+2\overrightarrow {OA}\cdot \overrightarrow {OB} $ 的最小值为 $ -\dfrac{4}{3} $ .

解析：

6.4.1 平面几何中的向量方法+6.4.2 向量在物理中的应用举例

一、刷基础

二、刷提升