6.4.3 课时2正弦定理
一、刷基础
1.在 $ △ABC $ 中,若内角 $ A $ , $ B $ , $ C $ 所对的边分别为 $ a $ , $ b $ , $ c $ ,则下列有关正弦定理及其变形错误的是( )
A. $ a:b= \sin A: \sin B $
B. $ a=b⇔ \sin 2A= \sin 2B $
C. $ \dfrac{a}{ \sin A}=\dfrac{b+c}{ \sin B+ \sin C} $
D. $ a=b⇔ \sin A= \sin B $
答案:B
解析:在 $ △ABC $ 中,由正弦定理得 $ \dfrac{a}{ \sin A}=\dfrac{b}{ \sin B}=\dfrac{c}{ \sin C}=k(k > 0) $ ,
则 $ a=k \sin A $ , $ b=k \sin B $ , $ c=k \sin C $ .
对于 $ \mathrm{A} $ , $ a:b= \sin A: \sin B $ ,故 $ \mathrm{A} $ 正确;
对于 $ \mathrm{B} $ ,当 $ A={30}^{\circ } $ , $ B={60}^{\circ } $ 时, $ \sin 2A= \sin 2B $ ,此时 $ b=\sqrt{3}a $ ,即 $ a\ne b $ ,故 $ \mathrm{B} $ 错误;
对于 $ \mathrm{C} $ , $ \dfrac{b+c}{ \sin B+ \sin C}=\dfrac{k \sin B+k \sin C}{ \sin B+ \sin C}=k=\dfrac{a}{ \sin A} $ ,故 $ \mathrm{C} $ 正确;
对于 $ \mathrm{D} $ , $ a=b⇔k \sin A=k \sin B⇔ \sin A= \sin B $ ,故 $ \mathrm{D} $ 正确.故选 $ \mathrm{B} $ .
2.已知 $ A $ , $ B $ 是 $ △ABC $ 的内角,则“ $ A < B $ ”是“ $ \sin A < \sin B $ ”的 条件.(填“充要”“充分不必要”“必要不充分”或“既不充分也不必要”)
解析:在 $ △ABC $ 中,若 $ A < B $ ,则 $ a < b $ ,由正弦定理得 $ \sin A < \sin B $ ;
若 $ \sin A < \sin B $ ,则由正弦定理得 $ a < b $ ,所以 $ A < B $ ,所以“ $ A < B $ ”是“ $ \sin A < \sin B $ ”的充要条件.
3.在 $ △ABC $ 中,内角 $ A $ , $ B $ , $ C $ 所对的边分别是 $ a $ , $ b $ , $ c $ ,已知 $ b=2 $ , $ A={45}^{\circ } $ , $ B={60}^{\circ } $ ,则 $ a= $ ( )
A. $ \dfrac{2\sqrt{6}}{3} $
B.2
C. $ 2\sqrt{2} $
D.4
答案:A
解析:已知 $ b=2 $ , $ A={45}^{\circ } $ , $ B={60}^{\circ } $ ,
由正弦定理可得 $ \dfrac{a}{ \sin A}=\dfrac{b}{ \sin B} $ ,则 $ a=\dfrac{b \sin A}{ \sin B}=\dfrac{2×\dfrac{\sqrt{2}}{2}}{\dfrac{\sqrt{3}}{2}}=\dfrac{2\sqrt{6}}{3} $ .故选 $ \mathrm{A} $ .
4.在 $ △ABC $ 中,内角 $ A $ , $ B $ , $ C $ 的对边分别为 $ a $ , $ b $ , $ c $ ,若 $ a=\sqrt{2} $ , $ A=\dfrac{\mathrm{\pi }}{6} $ , $ \cos C=\dfrac{1}{3} $ ,则 $ c= $ ( )
A. $ \dfrac{\sqrt{3}}{3} $
B. $ \dfrac{2}{3} $
C. $ \dfrac{8\sqrt{3}}{9} $
D. $ \dfrac{8}{3} $
答案:D
解析:由题可得 $ \sin C=\dfrac{2\sqrt{2}}{3} $ ,所以由正弦定理得 $ \dfrac{c}{ \sin C}=\dfrac{a}{ \sin A}⇒c=\dfrac{a \sin C}{ \sin A}=\dfrac{\sqrt{2}×\dfrac{2\sqrt{2}}{3}}{\dfrac{1}{2}}=\dfrac{8}{3} $ .故选 $ \mathrm{D} $ .
5.在 $ △ABC $ 中,内角 $ A $ , $ B $ , $ C $ 所对的边分别为 $ a $ , $ b $ , $ c $ ,已知 $ B={30}^{\circ } $ , $ b=2 $ , $ c=2\sqrt{2} $ ,则角 $ C $ 的大小为( )
A. $ {45}^{\circ } $
B. $ {105}^{\circ } $ 或 $ {15}^{\circ } $
C. $ {15}^{\circ } $
D. $ {135}^{\circ } $ 或 $ {45}^{\circ } $
答案:D
解析:由正弦定理得 $ \dfrac{b}{ \sin B}=\dfrac{c}{ \sin C} $ ,则 $ \sin C=\dfrac{c \sin B}{b}=\dfrac{2\sqrt{2} \sin {30}^{\circ }}{2}=\dfrac{\sqrt{2}}{2} $ ,因为 $ b < c $ ,所以 $ B < C < {180}^{\circ } $ ,所以角 $ C $ 为 $ {135}^{\circ } $ 或 $ {45}^{\circ } $ .故选 $ \mathrm{D} $ .
6.在 $ △ABC $ 中,内角 $ A $ , $ B $ , $ C $ 所对的边分别为 $ a $ , $ b $ , $ c $ ,若 $ a=4 $ , $ b=5 $ , $ \cos A=\dfrac{2\sqrt{2}}{3} $ ,则 $ \sin B= $ ( )
A. $ \dfrac{1}{3} $
B. $ \dfrac{5}{12} $
C. $ \dfrac{5}{6} $
D. $ \dfrac{1}{2} $
答案:B
解析:由 $ \cos A=\dfrac{2\sqrt{2}}{3} $ , $ A\in (0,\mathrm{\pi }) $ 得 $ \sin A > 0 $ ,则 $ \sin A=\sqrt{1-{ \cos }^{2}A}=\dfrac{1}{3} $ .由正弦定理得 $ \dfrac{a}{ \sin A}=\dfrac{b}{ \sin B} $ ,即 $ \dfrac{4}{\dfrac{1}{3}}=\dfrac{5}{ \sin B} $ ,得 $ \sin B=\dfrac{5}{12} $ .故选 $ \mathrm{B} $ .
7.在 $ △ABC $ 中,内角 $ A $ , $ B $ , $ C $ 所对的边分别为 $ a $ , $ b $ , $ c $ ,则下列判断正确的是( )
A. $ B={30}^{\circ } $ , $ c=4 $ , $ b=5 $ ,有两解
B. $ B={30}^{\circ } $ , $ c=4 $ , $ b=3.9 $ ,有一解
C. $ B={30}^{\circ } $ , $ c=4 $ , $ b=3 $ ,有一解
D. $ B={30}^{\circ } $ , $ c=4 $ , $ b=1 $ ,无解
答案:D
解析:选项 $ \mathrm{A} $ ,因为 $ b=5 > c=4 $ ,所以 $ B={30}^{\circ } > C $ , $ △ABC $ 只有一解,故 $ \mathrm{A} $ 错误;
选项 $ \mathrm{B} $ ,因为 $ c \sin {30}^{\circ }=2 < b=3.9 < c=4 $ ,所以 $ △ABC $ 有两解,故 $ \mathrm{B} $ 错误;
选项 $ \mathrm{C} $ ,因为 $ c \sin {30}^{\circ }=2 < b=3 < c=4 $ ,所以 $ △ABC $ 有两解,故 $ \mathrm{C} $ 错误;
选项 $ \mathrm{D} $ ,因为 $ b=1 < c \sin {30}^{\circ }=2 $ ,所以 $ △ABC $ 无解,故 $ \mathrm{D} $ 正确.
故选 $ \mathrm{D} $ .
8.在 $ △ABC $ 中,内角 $ A $ , $ B $ , $ C $ 的对边分别为 $ a $ , $ b $ , $ c $ ,其中 $ a=4 $ , $ B=\dfrac{\mathrm{\pi }}{4} $ ,若这个三角形有两组解,则 $ b $ 的取值范围为( )
A. $ (4,+\mathrm{\infty }) $
B. $ (0,2\sqrt{3}) $
C. $ (0,2\sqrt{2}) $
D. $ (2\sqrt{2},4) $
答案:D
解析:若这个三角形有两组解,则 $ a \sin B < b < a $ ,因为 $ a=4 $ , $ B=\dfrac{\mathrm{\pi }}{4} $ ,所以 $ 2\sqrt{2} < b < 4 $ .故选 $ \mathrm{D} $ .
9.在 $ △ABC $ 中,内角 $ A $ , $ B $ , $ C $ 的对边分别是 $ a $ , $ b $ , $ c $ ,且 $ {a}^{2}-{b}^{2}=\sqrt{3}bc $ , $ \sin C=\sqrt{3} \sin B $ ,则 $ A= $ ( )
A. $ {30}^{\circ } $
B. $ {60}^{\circ } $
C. $ {90}^{\circ } $
D. $ {120}^{\circ } $
答案:C
解析:在 $ △ABC $ 中,由 $ \sin C=\sqrt{3} \sin B $ 及正弦定理,得 $ c=\sqrt{3}b $ ,
又 $ {a}^{2}-{b}^{2}=\sqrt{3}bc $ ,则 $ a=2b $ ,显然 $ {b}^{2}+{c}^{2}=4{b}^{2}={a}^{2} $ ,所以 $ A={90}^{\circ } $ .故选 $ \mathrm{C} $ .
10.在 $ △ABC $ 中, $ a $ , $ b $ , $ c $ 分别为内角 $ A $ , $ B $ , $ C $ 所对的边,且 $ \dfrac{1}{2}c=b-a \cos C $ ,若 $ △ABC $ 的外接圆直径为 $ \dfrac{4\sqrt{3}}{3} $ ,则 $ a $ 的值为( )
A. $ \sqrt{3} $
B.2
C. $ 2\sqrt{3} $
D.4
答案:B
解析: $ \because \dfrac{1}{2}c=b-a \cos C $ , $ \therefore $ 由正弦定理得, $ \dfrac{1}{2} \sin C= \sin B- \sin A \cos C= \sin (A+C)- \sin A \cos C= \sin A \cos C+ \cos A \sin C- \sin A \cos C= \cos A \sin C $ ,
又在 $ △ABC $ 中, $ 0 < C < \mathrm{\pi } $ , $ 0 < A < \mathrm{\pi } $ ,
$ \therefore \sin C > 0 $ , $ \cos A=\dfrac{1}{2} $ , $ \therefore A=\dfrac{\mathrm{\pi }}{3} $ . $ \because △ABC $ 的外接圆直径为 $ \dfrac{4\sqrt{3}}{3} $ , $ \therefore \dfrac{a}{ \sin A}=\dfrac{4\sqrt{3}}{3} $ ,即 $ a=\dfrac{4\sqrt{3}}{3} \sin \dfrac{\mathrm{\pi }}{3}=2 $ .故选 $ \mathrm{B} $ .
11.在 $ △ABC $ 中,角 $ A $ , $ B $ , $ C $ 的对边分别为 $ a $ , $ b $ , $ c $ .若 $ a \cos C+c \cos A=a $ ,则 $ △ABC $ 的形状一定是( )
A.等腰三角形
B.锐角三角形
C.直角三角形
D.钝角三角形
答案:A
解析:在 $ △ABC $ 中,由 $ a \cos C+c \cos A=a $ 及正弦定理,得 $ \sin A \cos C+ \sin C \cos A= \sin A $ ,
则 $ \sin A= \sin (A+C)= \sin B $ .因为 $ 0 < A < \mathrm{\pi } $ , $ 0 < B < \mathrm{\pi } $ , $ 0 < A+B < \mathrm{\pi } $ ,所以 $ A=B $ ,所以 $ △ABC $ 是等腰三角形.故选 $ \mathrm{A} $ .
12.(多选)设 $ △ABC $ 的内角 $ A $ , $ B $ , $ C $ 所对的边分别为 $ a $ , $ b $ , $ c $ ,下列命题正确的有( )(多选)
A.若 $ { \cos }^{2}\frac{B}{2}=\dfrac{a+c}{2c} $ ,则 $ △ABC $ 为直角三角形
B.若 $ a-b=c \cos B-c \cos A $ ,则 $ △ABC $ 为直角三角形
C.若 $ c \cos B \cos A+b \cos A \cos C=b \cos B $ ,则 $ △ABC $ 为直角三角形
D.若 $ a=-c \cos (A+C) $ ,则 $ △ABC $ 为直角三角形
答案:AD
解析:对于 $ \mathrm{A} $ ,由 $ { \cos }^{2}\frac{B}{2}=\dfrac{a+c}{2c} $ ,可得 $ \dfrac{1+ \cos B}{2}=\dfrac{ \sin A+ \sin C}{2 \sin C}=\dfrac{1}{2}×\dfrac{ \sin A}{ \sin C}+\dfrac{1}{2} $ ,所以 $ 1+ \cos B=\dfrac{ \sin A}{ \sin C}+1 $ ,即 $ \cos B=\dfrac{ \sin A}{ \sin C} $ ,可得 $ \cos B \sin C= \sin A= \sin (B+C)= \sin B \cos C+ \cos B \sin C $ ,所以 $ \sin B \cos C=0 $ ,因为 $ B\in (0,\mathrm{\pi }) $ ,所以 $ \sin B > 0 $ ,所以 $ \cos C=0 $ ,又因为 $ C\in (0,\mathrm{\pi }) $ ,所以 $ C=\dfrac{\mathrm{\pi }}{2} $ ,所以 $ △ABC $ 为直角三角形,所以 $ \mathrm{A} $ 正确;
对于 $ \mathrm{B} $ ,因为 $ a-b=c \cos B-c \cos A $ ,所以 $ \sin A- \sin B= \sin C \cos B- \sin C \cos A $ ,
即 $ \sin (B+C)- \sin (A+C)= \sin C \cos B- \sin C \cos A $ ,所以 $ \sin B \cos C- \sin A \cos C=0 $ ,即 $ \cos C( \sin B- \sin A)=0 $ ,可得 $ \cos C=0 $ 或 $ \sin B= \sin A $ ,即 $ C=\dfrac{\mathrm{\pi }}{2} $ 或 $ A=B $ ,
所以 $ △ABC $ 是等腰三角形或直角三角形,所以 $ \mathrm{B} $ 错误;
对于 $ \mathrm{C} $ ,因为 $ c\cdot \cos B \cos A+b\cdot \cos A \cos C=b\cdot \cos B $ ,
所以 $ \sin C \cos B \cos A+ \sin B \cos A \cos C= \sin B \cos B $ ,即 $ \cos A \sin (B+C)= \sin B \cos B $ ,即 $ \sin 2A= \sin 2B $ ,
因为 $ A\in (0,\mathrm{\pi }) $ , $ B\in (0,\mathrm{\pi }) $ ,所以 $ 2A=2B $ 或 $ 2A+2B=\mathrm{\pi } $ ,所以 $ A=B $ 或 $ A+B=\dfrac{\mathrm{\pi }}{2} $ ,所以 $ △ABC $ 是等腰三角形或直角三角形,所以 $ \mathrm{C} $ 错误;
对于 $ \mathrm{D} $ ,因为 $ a=-c \cos (A+C)=-c \cos (\mathrm{\pi }-B)=c \cos B=c×\dfrac{{a}^{2}+{c}^{2}-{b}^{2}}{2ac} $ ,
整理可得 $ {a}^{2}+{b}^{2}={c}^{2} $ ,所以 $ △ABC $ 一定是直角三角形,所以 $ \mathrm{D} $ 正确.故选 $ \mathrm{A}\mathrm{D} $ .
二、刷提升
1.在 $ △ABC $ 中,内角 $ A $ , $ B $ , $ C $ 的对边分别为 $ a $ , $ b $ , $ c $ ,若 $ B={60}^{\circ } $ , $ b=3 $ ,则 $ \dfrac{a+c}{ \sin A+ \sin C}= $ ( )
A. $ \dfrac{\sqrt{3}}{6} $
B. $ \dfrac{1}{6} $
C. $ 2\sqrt{3} $
D.6
答案:C
解析:由正弦定理可得 $ \dfrac{a}{ \sin A}=\dfrac{c}{ \sin C}=\dfrac{b}{ \sin B} $ ,再由和比定理得 $ \dfrac{a+c}{ \sin A+ \sin C}=\dfrac{b}{ \sin B}=\dfrac{3}{\mathrm{ \sin }{60}^{\circ }}=\dfrac{3}{\dfrac{\sqrt{3}}{2}}=2\sqrt{3} $ .故选 $ \mathrm{C} $ .
2.在 $ △ABC $ 中,内角 $ A $ , $ B $ , $ C $ 的对边分别是 $ a $ , $ b $ , $ c $ ,且满足 $ c=3 $ , $ (2a-b) \cos C=c \cos B $ ,则 $ △ABC $ 外接圆的半径为( )
A. $ \sqrt{3} $
B.3
C. $ 2\sqrt{3} $
D.6
答案:A
解析:设 $ △ABC $ 外接圆的半径为 $ r(r > 0) $ .
在 $ △ABC $ 中,由余弦定理及 $ (2a-b) \cos C=c \cos B $ 可得 $ (2a-b)×\dfrac{{a}^{2}+{b}^{2}-{c}^{2}}{2ab}=c×\dfrac{{a}^{2}+{c}^{2}-{b}^{2}}{2ac} $ ,即 $ (2a-b)({a}^{2}+{b}^{2}-{c}^{2})=b({a}^{2}+{c}^{2}-{b}^{2}) $ ,
即 $ 2a({a}^{2}+{b}^{2}-{c}^{2})-b({a}^{2}+{b}^{2}-{c}^{2})=b({a}^{2}+{c}^{2}-{b}^{2}) $ ,
即 $ 2a({a}^{2}+{b}^{2}-{c}^{2})=b({a}^{2}+{b}^{2}-{c}^{2}+{a}^{2}+{c}^{2}-{b}^{2})=2{a}^{2}b $ ,即 $ {a}^{2}+{b}^{2}-{c}^{2}=ab $ .
$ \therefore $ 由余弦定理可得 $ \cos C=\dfrac{{a}^{2}+{b}^{2}-{c}^{2}}{2ab}=\dfrac{1}{2} $ .
$ \because C\in (0,\mathrm{\pi }) $ , $ \therefore \sin C=\dfrac{\sqrt{3}}{2} $ , $ \therefore $ 由正弦定理可得 $ 2r=\dfrac{c}{ \sin C}=\dfrac{3}{\dfrac{\sqrt{3}}{2}} $ ,解得 $ r=\sqrt{3} $ .故选 $ \mathrm{A} $ .
3.(多选)在 $ △ABC $ 中, $ AB=2 $ , $ C={30}^{\circ } $ ,若该三角形有且只有一解,则 $ AC $ 的值可能为( )(多选)
A.6
B.2
C.4
D.8
答案:BC
解析:在 $ △ABC $ 中, $ AB=2 $ , $ C={30}^{\circ } $ , $ {0}^{\circ } < B < {150}^{\circ } $ ,
由正弦定理,得 $ \sin B=\dfrac{AC \sin C}{AB}=\dfrac{1}{4}AC $ ,即 $ AC=4 \sin B $ .
当 $ B={90}^{\circ } $ 时, $ \sin B=1 $ , $ △ABC $ 有且只有一个解,此时 $ AC=4 $ ;
当 $ {30}^{\circ } < B < {150}^{\circ } $ ,且 $ B\ne {90}^{\circ } $ 时, $ \dfrac{1}{2} < \sin B < 1 $ , $ △ABC $ 有两解, $ 2 < AC < 4 $ ;
当 $ {0}^{\circ } < B\leqslant {30}^{\circ } $ 时, $ 0 < \sin B\leqslant \dfrac{1}{2} $ , $ △ABC $ 有且只有一个解, $ 0 < AC\leqslant 2 $ .
结合选项可知, $ AC $ 的值可能为2或4.故选 $ \mathrm{B}\mathrm{C} $ .
4.在 $ △ABC $ 中,内角 $ A $ , $ B $ , $ C $ 的对边分别为 $ a $ , $ b $ , $ c $ ,则“ $ a \cos B > c $ ”是“ $ △ABC $ 是钝角三角形”的( )
A.充分不必要条件
B.必要不充分条件
C.充要条件
D.既不充分也不必要条件
答案:A
解析:由 $ a \cos B > c $ 及正弦定理得 $ \sin A \cos B > \sin C $ ,
$ \because \sin C= \sin (A+B)= \sin A \cos B+ \cos A \sin B $ , $ \therefore \sin A \cos B > \sin A \cos B+ \cos A \sin B $ ,即 $ \cos A \sin B < 0 $ , $ \because A $ , $ B\in (0,\mathrm{\pi }) $ , $ \therefore \sin B > 0 $ , $ \therefore \cos A < 0 $ , $ \therefore A\in (\dfrac{\mathrm{\pi }}{2},\mathrm{\pi }) $ , $ \therefore △ABC $ 为钝角三角形,充分性成立;
若 $ △ABC $ 为钝角三角形,且 $ B $ 为钝角,则 $ \cos B < 0 $ , $ \therefore a \cos B < c $ ,必要性不成立.
综上所述,“ $ a \cos B > c $ ”是“ $ △ABC $ 是钝角三角形”的充分不必要条件.故选 $ \mathrm{A} $ .
5.在 $ △ABC $ 中, $ 2025{ \sin }^{2}C={ \sin }^{2}A+{ \sin }^{2}B $ ,则 $ \dfrac{( \tan A+ \tan B) \tan C}{ \tan A\cdot \tan B}= $ ( )
A. $ \dfrac{1}{2025} $
B. $ \dfrac{1}{2024} $
C. $ \dfrac{2}{2025} $
D. $ \dfrac{1}{1012} $
答案:D
解析:根据正弦定理,由 $ 2025{ \sin }^{2}C={ \sin }^{2}A+{ \sin }^{2}B $ 可得 $ 2025{c}^{2}={a}^{2}+{b}^{2} $ .
$ \dfrac{( \tan A+ \tan B) \tan C}{ \tan A\cdot \tan B}=\dfrac{(\dfrac{ \sin A}{ \cos A}+\dfrac{ \sin B}{ \cos B})×\dfrac{ \sin C}{ \cos C}}{\dfrac{ \sin A}{ \cos A}×\dfrac{ \sin B}{ \cos B}} $
$ =\dfrac{( \sin A \cos B+ \cos A \sin B)}{ \sin A \sin B}×\dfrac{ \sin C}{ \cos C} $
$ =\dfrac{ \sin (A+B)}{ \sin A \sin B}×\dfrac{ \sin C}{ \cos C} $ .
因为在 $ △ABC $ 中, $ A+B+C=\mathrm{\pi } $ ,所以 $ \sin (A+B)= \sin C $ ,
又根据余弦定理, $ \cos C=\dfrac{{a}^{2}+{b}^{2}-{c}^{2}}{2ab}=\dfrac{2025{c}^{2}-{c}^{2}}{2ab}=\dfrac{1012{c}^{2}}{ab} $ ,
故 $ \dfrac{( \tan A+ \tan B) \tan C}{ \tan A\cdot \tan B}=\dfrac{ \sin C}{ \sin A \sin B}×\dfrac{ \sin C}{ \cos C}=\dfrac{{c}^{2}}{ab}×\dfrac{ab}{1012{c}^{2}}=\dfrac{1}{1012} $ .故选 $ \mathrm{D} $ .
6.在 $ △ABC $ 中,内角 $ A $ , $ B $ , $ C $ 所对的边分别为 $ a $ , $ b $ , $ c $ ,下列判断正确的是( )(多选)
A.若 $ a > b $ ,则 $ \sin A > \sin B $
B.若 $ \sin A > \sin B $ ,则 $ A > B $
C.若 $ \sin A > \cos B $ ,则 $ △ABC $ 为锐角三角形
D.若 $ △ABC $ 为锐角三角形,则 $ \sin A > \cos B $
答案:ABD
解析:在 $ △ABC $ 中,若 $ a > b $ ,则根据正弦定理可得 $ \sin A > \sin B $ ,选项 $ \mathrm{A} $ 正确;
由 $ \sin A > \sin B $ 及正弦定理得 $ a > b $ ,则 $ A > B $ ,选项 $ \mathrm{B} $ 正确;
若 $ \sin A > \cos B $ ,即 $ \cos (\dfrac{\mathrm{\pi }}{2}-A) > \cos B $ ,当 $ \cos B < 0 $ , $ \cos (\dfrac{\mathrm{\pi }}{2}-A) > 0 $ 时, $ △ABC $ 为钝角三角形,选项 $ \mathrm{C} $ 错误;
若 $ △ABC $ 为锐角三角形,则 $ A+B > \dfrac{\mathrm{\pi }}{2} $ ,
则有 $ \dfrac{\mathrm{\pi }}{2} > A > \dfrac{\mathrm{\pi }}{2}-B > 0 $ ,
又正弦函数在 $ (0,\dfrac{\mathrm{\pi }}{2}) $ 上单调递增,
所以 $ \sin A > \sin (\dfrac{\mathrm{\pi }}{2}-B) $ ,即 $ \sin A > \cos B $ ,选项 $ \mathrm{D} $ 正确.故选 $ \mathrm{A}\mathrm{B}\mathrm{D} $ .
7.已知 $ a $ , $ b $ , $ c $ 分别是 $ △ABC $ 三个内角 $ A $ , $ B $ , $ C $ 的对边,下列关于 $ △ABC $ 形状的判断一定正确的为( )
A. 若 $ { \sin }^{2}A+{ \sin }^{2}B= \sin C $ ,则 $ △ABC $ 为直角三角形
B. 若 $ { \sin }^{2}A+{ \sin }^{2}B= \sin C $ ,则 $ △ABC $ 为等腰三角形
C. 若 $ { \sin }^{2}A+{ \sin }^{2}B+{ \sin }^{2}C=2 $ ,则 $ △ABC $ 为直角三角形
D. 若 $ { \sin }^{2}A+{ \sin }^{2}B+{ \sin }^{2}C=2 $ ,则 $ △ABC $ 为等腰三角形
答案:C
解析:对于A,B,当 $ { \sin }^{2}A+{ \sin }^{2}B= \sin C $ 时,由正弦定理可得 $ {a}^{2}+{b}^{2}=\dfrac{{c}^{2}}{ \sin C} $ ,即 $ \sin C=\dfrac{{c}^{2}}{{a}^{2}+{b}^{2}} $ ,因为 $ 0 < C < \mathrm{\pi } $ ,所以 $ 0 < \sin C\leqslant 1 $ ,所以 $ 0 < \dfrac{{c}^{2}}{{a}^{2}+{b}^{2}}\leqslant 1 $ ,即 $ 0 < {c}^{2}\leqslant {a}^{2}+{b}^{2} $ ,得 $ {a}^{2}+{b}^{2}-{c}^{2}\geqslant 0 $ ,所以 $ \cos C=\dfrac{{a}^{2}+{b}^{2}-{c}^{2}}{2ab}\geqslant 0 $ ,则 $ 0 < C\leqslant \dfrac{\mathrm{\pi }}{2} $ ,无法判断 $ △ABC $ 的形状,故A,B错误;
对于C,D,当 $ { \sin }^{2}A+{ \sin }^{2}B+{ \sin }^{2}C=2 $ 时,由 $ { \sin }^{2}C+{ \cos }^{2}C=1 $ ,得 $ { \sin }^{2}A+{ \sin }^{2}B+{ \sin }^{2}C=2({ \sin }^{2}C+{ \cos }^{2}C) $ ,整理得 $ { \sin }^{2}A+{ \sin }^{2}B-{ \sin }^{2}C=2{ \cos }^{2}C $ ,由正弦定理得 $ \dfrac{{a}^{2}+{b}^{2}-{c}^{2}}{{\left(2R\right) ^ {2}}}=2{ \cos }^{2}C $ ( $ R $ 是 $ △ABC $ 外接圆的半径),由余弦定理得 $ \dfrac{2ab \cos C}{{\left(2R\right) ^ {2}}}=2{ \cos }^{2}C $ ,所以由正弦定理得 $ \sin A \sin B \cos C={ \cos }^{2}C $ ,整理得 $ \cos C( \cos C- \sin A \sin B)=0 $ ,解得 $ C=\dfrac{\mathrm{\pi }}{2} $ 或 $ \sin A \sin B= \cos C=- \cos (A+B) $ ,即 $ \cos A \cos B=0 $ ,解得 $ A=\dfrac{\mathrm{\pi }}{2} $ 或 $ B=\dfrac{\mathrm{\pi }}{2} $ ,所以 $ △ABC $ 为直角三角形,故C正确,D错误.故选C.
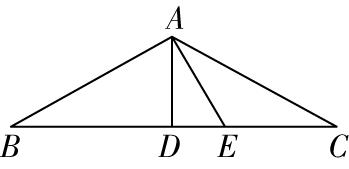
8.在 $ △ABC $ 中,已知 $ C=\dfrac{\mathrm{\pi }}{6} $ , $ \sin \mathrm{\angle }BAC= \cos B $ ,内角 $ A $ 的角平分线 $ AD $ 与 $ BC $ 交于点 $ D $ ,点 $ E $ 满足 $ \overrightarrow {BE}=2\overrightarrow {EC} $ ,则 $ \dfrac{AE}{AD}= $ ( )
A. $ \dfrac{\sqrt{3}}{3} $
B. $ \dfrac{\sqrt{3}}{2} $
C. $ \dfrac{2\sqrt{3}}{3} $
D. $ \sqrt{3} $
答案:C
解析:在 $ △ABC $ 中, $ C=\dfrac{\mathrm{\pi }}{6} $ , $ \sin \mathrm{\angle }BAC= \sin [\mathrm{\pi }-(B+C)]= \cos B $ ,
则 $ \cos B= \sin (B+C)= \sin (B+\dfrac{\mathrm{\pi }}{6})=\dfrac{\sqrt{3}}{2} \sin B+\dfrac{1}{2} \cos B $ ,整理可得 $ \tan B=\dfrac{\sqrt{3}}{3} $ .
因为 $ B\in (0,\dfrac{5\mathrm{\pi }}{6}) $ ,所以 $ B=\dfrac{\mathrm{\pi }}{6} $ ,所以 $ \mathrm{\angle }BAC=\dfrac{2\mathrm{\pi }}{3} $ , $ AC=AB $ .
如图所示,设 $ BC=3t(t > 0) $ ,因为 $ \overrightarrow {BE}=2\overrightarrow {EC} $ ,所以 $ BE=2t $ , $ CE=t $ .
在 $ △ABC $ 中,由正弦定理可得 $ \dfrac{AB}{ \sin C}=\dfrac{BC}{ \sin \mathrm{\angle }BAC} $ ,即 $ \dfrac{AB}{\dfrac{1}{2}}=\dfrac{3t}{\dfrac{\sqrt{3}}{2}} $ ,可得 $ AB=\sqrt{3}t $ ,所以 $ AC=\sqrt{3}t $ .
在 $ △ABE $ 中,由余弦定理可得 $ A{E}^{2}=A{B}^{2}+B{E}^{2}-2AB\cdot BE \cos \dfrac{\mathrm{\pi }}{6}=3{t}^{2}+4{t}^{2}-2\sqrt{3}t\cdot 2t\cdot \dfrac{\sqrt{3}}{2}={t}^{2} $ ,所以 $ AE=t $ .
因为 $ \mathrm{\angle }BAC $ 的角平分线 $ AD $ 与 $ BC $ 交于点 $ D $ ,所以 $ AD\perp BC $ ,所以 $ AD=AB \sin B=\sqrt{3}t×\dfrac{1}{2}=\dfrac{\sqrt{3}}{2}t $ ,故 $ \dfrac{AE}{AD}=\dfrac{t}{\dfrac{\sqrt{3}}{2}t}=\dfrac{2\sqrt{3}}{3} $ .故选 $ \mathrm{C} $ .
9.已知 $ △ABC $ 的内角 $ A $ , $ B $ , $ C $ 所对的边分别为 $ a $ , $ b $ , $ c $ ,若 $ \sqrt{3}b \sin A-a \cos B=2a $ ,则 $ B= $ .
答案: $ \dfrac{2\mathrm{\pi }}{3} $
解析:因为 $ \sqrt{3}b \sin A-a \cos B=2a $ ,所以由正弦定理得 $ \sqrt{3} \sin B \sin A- \sin A \cos B=2 \sin A $ .
因为 $ A\in (0,\mathrm{\pi }) $ ,所以 $ \sin A\ne 0 $ ,所以 $ \sqrt{3} \sin B- \cos B=2 $ ,
所以 $ \dfrac{\sqrt{3}}{2} \sin B-\dfrac{1}{2} \cos B=1 $ ,即 $ \sin B \cos \dfrac{\mathrm{\pi }}{6}- \cos B \sin \dfrac{\mathrm{\pi }}{6}=1 $ ,所以 $ \sin (B-\dfrac{\mathrm{\pi }}{6})=1 $ .
因为 $ B\in (0,\mathrm{\pi }) $ ,所以 $ -\dfrac{\mathrm{\pi }}{6} < B-\dfrac{\mathrm{\pi }}{6} < \dfrac{5\mathrm{\pi }}{6} $ ,
所以 $ B-\dfrac{\mathrm{\pi }}{6}=\dfrac{\mathrm{\pi }}{2} $ ,即 $ B=\dfrac{2\mathrm{\pi }}{3} $ .
10.已知在 $ △ABC $ 中,内角 $ A $ , $ B $ , $ C $ 所对的边分别是 $ a $ , $ b $ , $ c $ , $ a=4\sqrt{2} $ , $ \tan A=2\sqrt{2} $ .
(1) 求 $ △ABC $ 的外接圆半径;
(2) 求 $ △ABC $ 周长的最大值.
答案:(1) 【解】依题意, $ \begin{cases} \tan A=\dfrac{ \sin A}{ \cos A}=2\sqrt{2},\\ { \sin }^{2}A+{ \cos }^{2}A=1,\\ 0 < A < \dfrac{\mathrm{\pi }}{2},\end{cases} $
解得 $ \sin A=\dfrac{2\sqrt{2}}{3} $ , $ \cos A=\dfrac{1}{3} $ ,
故 $ △ABC $ 的外接圆半径 $ R=\dfrac{a}{2 \sin A}=\dfrac{4\sqrt{2}}{\dfrac{4\sqrt{2}}{3}}=3 $ .
(2) 由(1)知, $ \cos A=\dfrac{1}{3} $ ,
由余弦定理,得 $ {a}^{2}={b}^{2}+{c}^{2}-2bc \cos A={b}^{2}+{c}^{2}-\dfrac{2}{3}bc=(b+c)^{2}-\dfrac{8}{3}bc $ ,
因为 $ bc\leqslant \dfrac{{\left(b+c\right) ^ {2}}}{4} $ ,所以 $ -\dfrac{8}{3}bc\geqslant -\dfrac{2(b+c)^{2}}{3} $ ,
所以 $ 32\geqslant (b+c)^{2}-\dfrac{2 (b+c)^{2}}{3}=\dfrac{{\left(b+c \right) ^ {2}}}{3} $ ,
当且仅当 $ b=c=2\sqrt{6} $ 时等号成立,
故 $ b+c\leqslant 4\sqrt{6} $ ,
所以 $ △ABC $ 周长的最大值为 $ 4\sqrt{2}+4\sqrt{6} $ .
解析:
11.在 $ △ABC $ 中,内角 $ A $ , $ B $ , $ C $ 所对的边分别为 $ a $ , $ b $ , $ c $ ,且 $ b=6 $ , $ \cos A=-\dfrac{1}{3} $ . $ D $ 为线段 $ BC $ 上一点,且 $ BD=2DC $ , $ AD=\dfrac{\sqrt{129}}{3} $ .
(1) 求 $ c $ ;
(2) 求 $ \sin B $ .
答案:(1) 【解】因为 $ D $ 为线段 $ BC $ 上一点,且 $ BD=2DC $ ,
所以 $ \overrightarrow {BD}=\dfrac{2}{3}\overrightarrow {BC}=\dfrac{2}{3}(\overrightarrow {AC}-\overrightarrow {AB}) $ ,
所以 $ \overrightarrow {AD}=\overrightarrow {AB}+\overrightarrow {BD}=\dfrac{1}{3}\overrightarrow {AB}+\dfrac{2}{3}\overrightarrow {AC} $ .
因为 $ {|\overrightarrow {AD}|}^{2}={\left(\dfrac{1}{3}\overrightarrow {AB}+\dfrac{2}{3}\overrightarrow {AC}\right) ^ {2}} $ ,
所以 $ {|\overrightarrow {AD}|}^{2}=\dfrac{1}{9}{|\overrightarrow {AB}|}^{2}+\dfrac{4}{9}{|\overrightarrow {AC}|}^{2}+\dfrac{4}{9}\overrightarrow {AB}\cdot \overrightarrow {AC} $ ,即 $ \dfrac{129}{9}=\dfrac{1}{9}{c}^{2}+\dfrac{4}{9}×36+\dfrac{4}{9}×6c×(-\dfrac{1}{3}) $ ,
化简得 $ {c}^{2}-8c+15=0 $ ,解得 $ c=3 $ 或 $ c=5 $ .
(2) 因为 $ \cos A=-\dfrac{1}{3} $ ,且 $ 0 < A < \mathrm{\pi } $ ,
所以 $ \sin A=\sqrt{1-{ \cos }^{2}A}=\dfrac{2\sqrt{2}}{3} $ .
由余弦定理得 $ {a}^{2}={b}^{2}+{c}^{2}-2bc \cos A=36+{c}^{2}-12c×(-\dfrac{1}{3})=36+{c}^{2}+4c $ ,
当 $ c=3 $ 时, $ a=\sqrt{57} $ ,
由正弦定理得 $ \dfrac{a}{ \sin A}=\dfrac{b}{ \sin B}⇒ \sin B=\dfrac{b \sin A}{a}=\dfrac{6×\dfrac{2\sqrt{2}}{3}}{\sqrt{57}}=\dfrac{4\sqrt{114}}{57} $ ;
当 $ c=5 $ 时, $ a=9 $ ,此时 $ \sin B=\dfrac{b \sin A}{a}=\dfrac{6×\dfrac{2\sqrt{2}}{3}}{9}=\dfrac{4\sqrt{2}}{9} $ .
解析:
12.在锐角三角形 $ ABC $ 中,内角 $ A $ , $ B $ , $ C $ 所对的边分别为 $ a $ , $ b $ , $ c $ ,且 $ c+b=2a \cos B $ .
(1) 证明: $ A=2B $ ;
(2) 求 $ \dfrac{c}{a} $ 的取值范围.
答案:(1) 【证明】因为 $ c+b=2a \cos B $ ,所以 $ \sin C+ \sin B=2 \sin A \cos B $ ,
所以 $ \sin (A+B)+ \sin B=2 \sin A \cos B $ ,
即 $ \sin A \cos B+ \cos A \sin B+ \sin B=2 \sin A \cos B $ ,
整理得 $ \sin B= \sin A \cos B- \cos A \sin B= \sin (A-B) $ .
因为 $ 0 < A < \dfrac{\mathrm{\pi }}{2} $ , $ 0 < B < \dfrac{\mathrm{\pi }}{2} $ ,所以 $ -\dfrac{\mathrm{\pi }}{2} < A-B < \dfrac{\mathrm{\pi }}{2} $ ,
所以 $ B=A-B $ ,故 $ A=2B $ .
(2) 【解】由(1)知, $ A=2B $ ,则在锐角三角形 $ ABC $ 中,满足 $ \begin{cases}0 < A=2B < \dfrac{\mathrm{\pi }}{2},\\ 0 < C=\mathrm{\pi }-3B < \dfrac{\mathrm{\pi }}{2},\end{cases} $
解得 $ \dfrac{\mathrm{\pi }}{6} < B < \dfrac{\mathrm{\pi }}{4} $ ,故 $ \sqrt{2} < 2 \cos B < \sqrt{3} $ .
由题意得, $ \dfrac{c}{a}=\dfrac{ \sin C}{ \sin A}=\dfrac{ \sin 3B}{ \sin 2B}=\dfrac{ \sin 2B \cos B+ \cos 2B \sin B}{ \sin 2B}= \cos B+\dfrac{2{ \cos }^{2}B-1}{2 \cos B}=2 \cos B-\dfrac{1}{2 \cos B} $ ,
令 $ 2 \cos B=t\in (\sqrt{2},\sqrt{3}) $ ,
因为 $ f(t)=t-\dfrac{1}{t} $ 在 $ (\sqrt{2},\sqrt{3}) $ 上单调递增,所以 $ \dfrac{\sqrt{2}}{2} < f(t) < \dfrac{2\sqrt{3}}{3} $ ,
所以 $ \dfrac{c}{a} $ 的取值范围为 $ (\dfrac{\sqrt{2}}{2},\dfrac{2\sqrt{3}}{3}) $ .
解析:
13.在 $ △ABC $ 中,角 $ A $ , $ B $ , $ C $ 所对的边分别为 $ a $ , $ b $ , $ c $ ,若 $ a=8 $ , $ b=5 $ , $ \cos A=\dfrac{3}{5} $ ,则角 $ B $ 为( )
A. $ \dfrac{\mathrm{\pi }}{6} $
B. $ \dfrac{\mathrm{\pi }}{3} $
C. $ \dfrac{\mathrm{\pi }}{6} $ 和 $ \dfrac{5\mathrm{\pi }}{6} $
D. $ \dfrac{\mathrm{\pi }}{3} $ 和 $ \dfrac{2\mathrm{\pi }}{3} $
答案:A
解析:因为 $ \cos A=\dfrac{3}{5} $ , $ 0 < A < \mathrm{\pi } $ ,所以 $ \sin A=\sqrt{1-{ \cos }^{2}A}=\dfrac{4}{5} $ ,
由正弦定理可得 $ \dfrac{a}{ \sin A}=\dfrac{b}{ \sin B} $ ,则 $ \sin B=\dfrac{b\cdot \sin A}{a}=\dfrac{5×\dfrac{4}{5}}{8}=\dfrac{1}{2} $ .
因为 $ B\in (0,\mathrm{\pi }) $ ,所以 $ B=\dfrac{\mathrm{\pi }}{6} $ 或 $ \dfrac{5\mathrm{\pi }}{6} $ .又 $ b < a $ ,所以 $ B < A $ ,则 $ B=\dfrac{\mathrm{\pi }}{6} $ .故选 $ \mathrm{A} $ .
14.在 $ △ABC $ 中,内角 $ A $ , $ B $ , $ C $ 所对的边分别为 $ a $ , $ b $ , $ c.a=\sqrt{3} $ , $ b=\sqrt{2} $ , $ B={45}^{\circ } $ ,求角 $ A $ , $ C $ 和边 $ c $ .
答案:【解】由正弦定理 $ \dfrac{a}{ \sin A}=\dfrac{b}{ \sin B} $ ,得 $ \sin A=\dfrac{\sqrt{3}}{2} $ .因为 $ a > b $ ,所以 $ A={60}^{\circ } $ 或 $ A={120}^{\circ } $ .
当 $ A={60}^{\circ } $ 时, $ C={180}^{\circ }-{45}^{\circ }-{60}^{\circ }={75}^{\circ } $ , $ c=\dfrac{b \sin C}{ \sin B}=\dfrac{\sqrt{6}+\sqrt{2}}{2} $ .
当 $ A={120}^{\circ } $ 时, $ C={180}^{\circ }-{45}^{\circ }-{120}^{\circ }={15}^{\circ } $ , $ c=\dfrac{b \sin C}{ \sin B}=\dfrac{\sqrt{6}-\sqrt{2}}{2} $ .
解析:
15.在锐角三角形 $ ABC $ 中, $ a $ , $ b $ , $ c $ 分别是内角 $ A $ , $ B $ , $ C $ 的对边.若 $ B=2A $ ,则 $ \dfrac{b}{a} $ 的取值范围是( )
A. $ (-2,2) $
B. $ (0,2) $
C. $ (\sqrt{2} $ , $ \sqrt{3}) $
D. $ (\sqrt{2},2) $
答案:C
解析: $ \because B=2A $ , $ \therefore \sin B= \sin 2A $ .由正弦定理得 $ \dfrac{b}{a}=\dfrac{ \sin B}{ \sin A}=\dfrac{ \sin 2A}{ \sin A}=2 \cos A.\because 0 < 2A < \dfrac{\mathrm{\pi }}{2} $ , $ 0 < \mathrm{\pi }-3A < \dfrac{\mathrm{\pi }}{2} $ , $ \therefore \dfrac{\mathrm{\pi }}{6} < A < \dfrac{\mathrm{\pi }}{4} $ , $ \therefore \dfrac{\sqrt{2}}{2} < \cos A < \dfrac{\sqrt{3}}{2} $ , $ \sqrt{2} < 2 \cos A < \sqrt{3} $ .故选C.
16.在 $ △ABC $ 中,内角 $ A $ , $ B $ , $ C $ 所对的边分别为 $ a $ , $ b $ , $ c $ ,已知 $ 2{ \cos }^{2}\frac{A}{2}=\dfrac{\sqrt{3}}{3} \sin A $ .若 $ a=2\sqrt{3} $ ,则 $ △ABC $ 周长的取值范围为 .
答案: $ (4\sqrt{3},4+2\sqrt{3}] $
解析:由 $ 2{ \cos }^{2}\frac{A}{2}=\dfrac{\sqrt{3}}{3} \sin A $ 得 $ 1+ \cos A=\dfrac{\sqrt{3}}{3} \sin A $ ,即 $ \dfrac{\sqrt{3}}{3} \sin A- \cos A=1 $ ,
$ \therefore \dfrac{2\sqrt{3}}{3} \sin (A-\dfrac{\mathrm{\pi }}{3})=1 $ ,
即 $ \sin (A-\dfrac{\mathrm{\pi }}{3})=\dfrac{\sqrt{3}}{2} $ .
$ \because 0 < A < \mathrm{\pi } $ , $ \therefore -\dfrac{\mathrm{\pi }}{3} < A-\dfrac{\mathrm{\pi }}{3} < \dfrac{2\mathrm{\pi }}{3} $ ,
$ \therefore A-\dfrac{\mathrm{\pi }}{3}=\dfrac{\mathrm{\pi }}{3} $ ,即 $ A=\dfrac{2\mathrm{\pi }}{3} $ .
$ \because \dfrac{a}{ \sin A}=\dfrac{b}{ \sin B}=\dfrac{c}{ \sin C}=\dfrac{2\sqrt{3}}{\dfrac{\sqrt{3}}{2}}=4 $ ,
$ \therefore b=4 \sin B $ , $ c=4 \sin C $ .
则 $ b+c=4 \sin B+4 \sin C $
$ =4 \sin B+4 \sin (\dfrac{\mathrm{\pi }}{3}-B) $
$ =4 \sin B+4(\dfrac{\sqrt{3}}{2} \cos B-\dfrac{1}{2} \sin B) $
$ =2 \sin B+2\sqrt{3} \cos B=4 \sin (B+\dfrac{\mathrm{\pi }}{3}) $ .
$ \because 0 < B < \dfrac{\mathrm{\pi }}{3} $ , $ \therefore \dfrac{\mathrm{\pi }}{3} < B+\dfrac{\mathrm{\pi }}{3} < \dfrac{2\mathrm{\pi }}{3} $ .
则 $ \dfrac{\sqrt{3}}{2} < \sin (B+\dfrac{\mathrm{\pi }}{3})\leqslant 1 $ ,
即 $ 2\sqrt{3} < 4 \sin (B+\dfrac{\mathrm{\pi }}{3})\leqslant 4 $ ,
则 $ 2\sqrt{3} < b+c\leqslant 4 $ ,则 $ 4\sqrt{3} < a+b+c\leqslant 4+2\sqrt{3} $ ,
即 $ △ABC $ 周长的取值范围为 $ (4\sqrt{3},4+2\sqrt{3}] $ .
17.在 $ △ABC $ 中,内角 $ A $ , $ B $ , $ C $ 所对的边分别为 $ a $ , $ b $ , $ c $ .若 $ ({a}^{2}+{b}^{2}) \sin (A-B)=({a}^{2}-{b}^{2}) \sin (A+B) $ ,试判断 $ △ABC $ 的形状.
答案:【解】因为 $ ({a}^{2}+{b}^{2}) \sin (A-B)=({a}^{2}-{b}^{2}) \sin (A+B) $ ,
所以 $ {b}^{2}[ \sin (A+B)+ \sin (A-B)]={a}^{2}[ \sin (A+B)- \sin (A-B)] $ ,
所以 $ 2 \sin A \cos B\cdot {b}^{2}=2 \cos A \sin B\cdot {a}^{2} $ ,
即 $ {a}^{2} \cos A \sin B={b}^{2} \sin A \cos B $ .
由正弦定理知 $ a=2R \sin A $ , $ b=2R \sin B $ ( $ R $ 为 $ △ABC $ 外接圆的半径),
所以 $ { \sin }^{2}A \cos A \sin B={ \sin }^{2}B \sin A \cos B $ .
又 $ \sin A \sin B\ne 0 $ ,所以 $ \sin A \cos A= \sin B \cos B $ ,
所以 $ \sin 2A= \sin 2B $ .
因为在 $ △ABC $ 中, $ 0 < 2A < 2\mathrm{\pi } $ , $ 0 < 2B < 2\mathrm{\pi } $ ,
所以 $ 2A=2B $ 或 $ 2A=\mathrm{\pi }-2B $ ,所以 $ A=B $ 或 $ A+B=\dfrac{\mathrm{\pi }}{2} $ .
所以 $ △ABC $ 为等腰三角形或直角三角形.
解析:
