6.4.3 课时3与三角形面积相关的问题

在 $ △ABC $ 中, $ AB=4 $ , $ AC=3 $ , $ \mathrm{\angle }BAC=\dfrac{\mathrm{\pi }}{6} $ ,则 $ △ABC $ 的面积 $ S=\dfrac{1}{2}AB×AC× \sin \mathrm{\angle }BAC=\dfrac{1}{2}×4×3×\dfrac{1}{2}=3 $ .故选 $ \mathrm{B} $ .

$ \because {b}^{2}-40={\left(a-c\right) ^ {2}} $ , $ \therefore {b}^{2}={a}^{2}+{c}^{2}-2ac+40 $ , $ \therefore \cos B=\dfrac{{a}^{2}+{c}^{2}-{b}^{2}}{2ac}=\dfrac{2ac-40}{2ac}=\dfrac{1}{2} $ ,则 $ ac=40 $ , $ \therefore △ABC $ 的面积为 $ \dfrac{1}{2}ac \sin B=\dfrac{1}{2}×40×\dfrac{\sqrt{3}}{2}=10\sqrt{3} $ .故选 $ \mathrm{A} $ .

如图,延长 $ AD $ 到点 $ E $ 使 $ DE=AD $ ,连接 $ CE $ ,

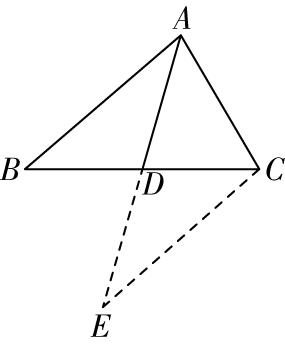
又 $ \because BD=DC $ , $ \mathrm{\angle }ADB=\mathrm{\angle }CDE $ , $ \therefore △ABD≌△ECD(\mathrm{S}\mathrm{A}\mathrm{S}) $ ,

$ \therefore CE=AB=2\sqrt{2} $ , $ AE=2\sqrt{5} $ , $ △ABC $ 的面积等于 $ △ACE $ 的面积.

在 $ △ACE $ 中,由余弦定理得 $ \cos \mathrm{\angle }ACE=\dfrac{A{C}^{2}+C{E}^{2}-A{E}^{2}}{2AC\cdot CE}=\dfrac{6+8-20}{2×\sqrt{6}×2\sqrt{2}}=-\dfrac{\sqrt{3}}{4} $ ,

又 $ 0 < \mathrm{\angle }ACE < \mathrm{\pi } $ ,

$ \therefore \sin \mathrm{\angle }ACE=\sqrt{1-\dfrac{3}{16}}=\dfrac{\sqrt{13}}{4} $ ,

$ \therefore S={S}_{△ACE}=\dfrac{1}{2}AC\cdot CE \sin \mathrm{\angle }ACE=\dfrac{1}{2}×\sqrt{6}×2\sqrt{2}×\dfrac{\sqrt{13}}{4}=\dfrac{\sqrt{39}}{2} $ .故选 $ \mathrm{C} $ .

在 $ △ABC $ 中,记角 $ A $ , $ B $ , $ C $ 所对的边分别为 $ a $ , $ b $ , $ c $ ,

因为 $ {S}_{△ABC}={S}_{△ABD}+{S}_{△CBD} $ ,

所以 $ \dfrac{1}{2}ac \sin \dfrac{\mathrm{\pi }}{3}=\dfrac{1}{2}×2c \sin \dfrac{\mathrm{\pi }}{6}+\dfrac{1}{2}×2a \sin \dfrac{\mathrm{\pi }}{6} $ ,即 $ a+c=\dfrac{\sqrt{3}}{2}ac $ ,所以 $ 2\sqrt{ac}\leqslant \dfrac{\sqrt{3}}{2}ac $ ,即 $ ac\geqslant \dfrac{16}{3} $ ,当且仅当 $ a=c=\dfrac{4\sqrt{3}}{3} $ 时等号成立,

所以 $ {S}_{△ABC}=\dfrac{1}{2}ac \sin \dfrac{\mathrm{\pi }}{3}=\dfrac{\sqrt{3}}{4}ac\geqslant \dfrac{4\sqrt{3}}{3} $ .

故选 $ \mathrm{D} $ .

$ \because \sqrt{3}(a \cos \text{ }C+c \cos \text{ }A)=2b \sin \text{ }B $ , $ \therefore $ 由正弦定理可得 $ \sqrt{3}( \sin \text{ }A \cos \text{ }C+ \sin \text{ }C \cos \text{ }A)=2{ \sin }^{2}B $ , $ \therefore \sqrt{3} \sin (A+C)=2{ \sin }^{2}B $ , $ \therefore \sqrt{3} \sin \text{ }B=2{ \sin }^{2}B $ .又 $ \because \sin \text{ }B\text{ }\ne 0 $ , $ \therefore \sin \text{ }B=\dfrac{\sqrt{3}}{2} $ . $ \because \mathrm{\angle }CAB=\dfrac{\mathrm{\pi }}{3} $ , $ \therefore B\in (0,\dfrac{2\mathrm{\pi }}{3}) $ , $ \therefore B=\dfrac{\mathrm{\pi }}{3} $ ， $ \therefore \mathrm{\angle }ACB=\mathrm{\pi }-\mathrm{\angle }CAB-B=\dfrac{\mathrm{\pi }}{3} $ ,因此 $ \mathrm{A} $ , $ \mathrm{B} $ 正确.四边形 $ ABCD $ 的面积等于 $ {S}_{△ABC}+{S}_{△ACD}=\dfrac{\sqrt{3}}{4}A{C}^{2}+\dfrac{1}{2}AD\cdot DC\cdot \sin \mathrm{\angle }ADC=\dfrac{\sqrt{3}}{4}(A{D}^{2}+D{C}^{2}-2AD\cdot DC\cdot \cos \mathrm{\angle }ADC)+\dfrac{1}{2}AD\cdot DC\cdot \sin \mathrm{\angle }ADC=\dfrac{\sqrt{3}}{4}×(9+1-6 \cos \mathrm{\angle }ADC)+\dfrac{1}{2}×3×1\cdot \sin \mathrm{\angle }ADC=\dfrac{5\text{  }\sqrt{3}}{2}+3 \sin (\mathrm{\angle }ADC-\dfrac{\mathrm{\pi }}{3})\leqslant \dfrac{5\text{  }\sqrt{3}}{2}+3 $ ,当且仅当 $ \mathrm{\angle }ADC-\dfrac{\mathrm{\pi }}{3}=\dfrac{\mathrm{\pi }}{2} $ ,即 $ \mathrm{\angle }ADC=\dfrac{5\mathrm{\pi }}{6} $ 时，等号成立,因此 $ \mathrm{C} $ 正确， $ \mathrm{D} $ 错误.故选 $ \mathrm{A}\mathrm{B}\mathrm{C} $ .

由 $ {S}_{△ABC}=\dfrac{1}{2}AB\cdot AC\cdot \sin \mathrm{\angle }BAC=12 \sin \mathrm{\angle }BAC=8\sqrt{2} $ ，得 $ \sin \mathrm{\angle }BAC=\dfrac{2\sqrt{2}}{3} $ ，

$ \because \mathrm{\angle }BAC $ 为锐角， $ \therefore \cos \mathrm{\angle }BAC=\sqrt{1-{ \sin }^{2}\mathrm{\angle }BAC}=\dfrac{1}{3} $ .

$ \because \overrightarrow {BM}=\overrightarrow {MC} $ ， $ \therefore M $ 为 $ BC $ 的中点，

$ \therefore \overrightarrow {AM}=\dfrac{1}{2}(\overrightarrow {AB}+\overrightarrow {AC}) $ ，

$ \therefore |\overrightarrow {AM}|=\dfrac{1}{2}\sqrt{{\left(\overrightarrow {AB}+\overrightarrow {AC}\right) ^ {2}}} $

$ =\dfrac{1}{2}\sqrt{{\overrightarrow {AB}}^{2}+{\overrightarrow {AC}}^{2}+2\overrightarrow {AB}\cdot \overrightarrow {AC}} $

$ =\dfrac{1}{2}×\sqrt{36+16+2×6×4×\dfrac{1}{3}}=\sqrt{17} $ .

故选 $ \mathrm{B} $ .

由余弦定理得 $ {a}^{2}+{b}^{2}-{c}^{2}=2ab \cos C $ ,

由三角形面积公式得 $ S=\dfrac{1}{2}ab \sin C $ ,

又 $ S=\dfrac{{a}^{2}+{b}^{2}-{c}^{2}}{4} $ ,所以 $ \dfrac{1}{2}ab \sin C=\dfrac{2ab \cos C}{4} $ .

因为 $ a > 0 $ , $ b > 0 $ ,所以 $ \dfrac{ \sin C}{ \cos C}=1 $ ,即 $ \tan C=1 $ .

又 $ {0}^{\circ } < C < {180}^{\circ } $ ,所以 $ C={45}^{\circ } $ .故选 $ \mathrm{C} $ .

由 $ a \cos C+\sqrt{3}a \sin C-b-c=0 $ 及正弦定理得 $ \sin A \cos C+\sqrt{3} \sin A \sin C= \sin B+ \sin C $ ,

$ \because B=\mathrm{\pi }-(A+C) $ ,

$ \therefore \sqrt{3} \sin A \sin C= \cos A \sin C+ \sin C $ .

$ \because 0 < C < \mathrm{\pi } $ , $ \therefore \sin C\ne 0 $ , $ \therefore \sqrt{3} \sin A- \cos A=1 $ , $ \therefore \sin (A-\dfrac{\mathrm{\pi }}{6})=\dfrac{1}{2} $ .又 $ 0 < A < \mathrm{\pi } $ , $ \therefore -\dfrac{\mathrm{\pi }}{6} < A-\dfrac{\mathrm{\pi }}{6} < \dfrac{5\mathrm{\pi }}{6} $ , $ \therefore A-\dfrac{\mathrm{\pi }}{6}=\dfrac{\mathrm{\pi }}{6} $ ,即 $ A=\dfrac{\mathrm{\pi }}{3} $ .

$ \because {S}_{△ABC}=\dfrac{1}{2}bc \sin A=6\sqrt{3} $ , $ \therefore bc=24 $ .由余弦定理得 $ {a}^{2}=49={b}^{2}+{c}^{2}-2bc \cos A $ ,

得 $ {b}^{2}+{c}^{2}=73 $ ,则 $ (b+c)^{2}={b}^{2}+{c}^{2}+2bc=73+48=121 $ ,故 $ b+c=11 $ , $ \therefore △ABC $ 的周长为 $ a+b+c=18 $ .故选 $ \mathrm{C} $ .

由正弦定理及 $ \sin B \sin C=\sqrt{3} \sin A $ 得 $ \sin C=\dfrac{\sqrt{3} \sin A}{ \sin B}=\dfrac{\sqrt{3}a}{b} $ ，所以 $ {S}_{△ABC}=\dfrac{1}{2}ab \sin C=\dfrac{\sqrt{3}}{2}{a}^{2}=\dfrac{3\sqrt{3}}{2} $ ，解得 $ a=\sqrt{3} $ .又 $ a+b=3\sqrt{3} $ ，所以 $ b=2\sqrt{3} $ ，则 $ \sin C=\dfrac{\sqrt{3}a}{b}=\dfrac{\sqrt{3}}{2} $ ，所以 $ \cos C=±\sqrt{1-{ \sin }^{2}C}=±\dfrac{1}{2} $ .

当 $ \cos C=\dfrac{1}{2} $ 时，

$ c=\sqrt{3+12-2×\sqrt{3}×2\sqrt{3}×\dfrac{1}{2}}=3 $ ；

当 $ \cos C=-\dfrac{1}{2} $ 时，

$ c=\sqrt{3+12-2×\sqrt{3}×2\sqrt{3}×(-\dfrac{1}{2})}=\sqrt{21} $ .

综上， $ c=3 $ 或 $ \sqrt{21} $ ，故选 $ \mathrm{D} $ ．

由三角形面积公式,得 $ {S}_{△ABC}=\dfrac{1}{2}AB\cdot BC\cdot \sin B=\dfrac{1}{2} $ .

又 $ \because AB=1 $ , $ BC=\sqrt{2} $ , $ \therefore \sin B=\dfrac{\sqrt{2}}{2} $ .

$ \because B\in (0,\mathrm{\pi }) $ , $ \therefore B=\dfrac{\mathrm{\pi }}{4} $ 或 $ B=\dfrac{3\mathrm{\pi }}{4} $ .由余弦定理得 $ A{C}^{2}=A{B}^{2}+B{C}^{2}-2AB\cdot BC \cos B $ .当 $ B=\dfrac{\mathrm{\pi }}{4} $ 时,得 $ AC=1 $ ,这时不符合 $ △ABC $ 为钝角三角形的要求,故舍去；当 $ B=\dfrac{3\mathrm{\pi }}{4} $ 时,得 $ AC=\sqrt{5} $ .故选 $ \mathrm{B} $ .