1．在某次测量中，设点 $ A $ 在点 $ B $ 的南偏东 $ {34}^{\circ }27\prime $ 方向，则点 $ B $ 在点 $ A $ 的（ ）
A．北偏西 $ {34}^{\circ }27\prime $ 方向
B．北偏东 $ {55}^{\circ }33\prime $ 方向
C．北偏西 $ {55}^{\circ }32\prime $ 方向
D．南偏西 $ {55}^{\circ }33\prime $ 方向
如图所示，因为点 $ A $ 在点 $ B $ 的南偏东 $ {34}^{\circ }27\prime $ 方向，所以点 $ B $ 在点 $ A $ 的北偏西 $ {34}^{\circ }27\prime $ 方向，故选 $ \mathrm{A} $ .
2．如图，前卫斜塔位于辽宁省葫芦岛市绥中县，始建于辽代，又名瑞州古塔，其倾斜度（塔与地面所成的角）远超著名的意大利比萨斜塔.现有一个斜塔的塔身长 $ 10\mathrm{m} $ ，一旅游者在正午时分（太阳光线与地面垂直）测得塔在地面上的投影长为 $ 5\mathrm{m} $ ，则该塔的倾斜度（塔与地面所成的角）为（ ）
A． $ {60}^{\circ } $
B． $ {45}^{\circ } $
C． $ {30}^{\circ } $
D． $ {15}^{\circ } $
如图所示,线段 $ AC $ 表示塔身,线段 $ AB $ 为塔在地面上的投影, $ CB\perp AB $ ,所以在 $ \mathrm{R}\mathrm{t}△ABC $ 中, $ \cos A=\dfrac{AB}{AC}=\dfrac{1}{2} $ .
因为 $ {0}^{\circ } < A < {90}^{\circ } $ ,所以 $ A={60}^{\circ } $ ,故选 $ \mathrm{A} $ .
3．如图所示，在坡度一定的山坡 $ A $ 处测得山顶上一建筑物 $ CD $ 的顶端 $ C $ 对于山坡的斜度为 $ {15}^{\circ } $ ，向山顶前进 $ 100\mathrm{m} $ 到达 $ B $ 处，又测得 $ C $ 对于山坡的斜度为 $ {45}^{\circ } $ .若 $ CD=50\mathrm{m} $ ，山坡对于地平面的坡度为 $ \theta $ ，则 $ \cos \theta = $ （ ）
A． $ \dfrac{\sqrt{3}}{2} $
B． $ \dfrac{\sqrt{2}}{2} $
C． $ \sqrt{3}-1 $
D． $ \sqrt{2}-1 $
由题意得 $ \mathrm{\angle }ACB={30}^{\circ } $ ,在 $ △ABC $ 中,由正弦定理得 $ \dfrac{AB}{ \sin {30}^{\circ }}=\dfrac{AC}{ \sin {135}^{\circ }} $ ,
$ \therefore AC=100\sqrt{2} $ ．
在 $ △ADC $ 中, $ \dfrac{AC}{ \sin (\theta +{90}^{\circ })}=\dfrac{CD}{ \sin {15}^{\circ }} $ ,
$ \therefore \cos \theta = \sin (\theta +{90}^{\circ })=\dfrac{AC\cdot \sin {15}^{\circ }}{CD}=\sqrt{3}-1 $ .故选 $ \mathrm{C} $ .
4．如图，一艘船航行到点 $ B $ 处时，测得灯塔 $ A $ 在其北偏西 $ {60}^{\circ } $ 的方向上，随后该船以20海里/时的速度，往正北方向航行两小时后到达点 $ C $ ，测得灯塔 $ A $ 在其南偏西 $ {75}^{\circ } $ 的方向上，此时船与灯塔 $ A $ 间的距离为（ ）
A． $ 20\sqrt{3} $ 海里
B． $ 40\sqrt{3} $ 海里
C． $ 20\sqrt{6} $ 海里
D． $ 40\sqrt{6} $ 海里
依题意,在 $ △ABC $ 中, $ B={60}^{\circ } $ , $ C={75}^{\circ } $ ,则 $ A={45}^{\circ } $ ,而 $ BC=40 $ ,由正弦定理得 $ \dfrac{AC}{ \sin B}=\dfrac{BC}{ \sin A} $ ,则 $ AC=\dfrac{BC \sin B}{ \sin A}=\dfrac{40\sqrt{3}}{\sqrt{2}}=20\sqrt{6} $ ,所以船与灯塔 $ A $ 间的距离为 $ 20\sqrt{6} $ 海里.故选 $ \mathrm{C} $ .
5．为加快推进“ $ 5\mathrm{G}+ $ 光网”双千兆城市建设，如图，在东北某地地面有四个 $ 5\mathrm{G} $ 基站 $ A $ ， $ B $ ， $ C $ ， $ D $ .已知 $ C $ ， $ D $ 两个基站建在松花江的南岸，距离为 $ 10\sqrt{3}\mathrm{k}\mathrm{m} $ ；基站 $ A $ ， $ B $ 在江的北岸，测得 $ \mathrm{\angle }ACB={75}^{\circ } $ ， $ \mathrm{\angle }ACD={120}^{\circ } $ ， $ \mathrm{\angle }ADC={30}^{\circ } $ ， $ \mathrm{\angle }ADB={45}^{\circ } $ ，则 $ A $ ， $ B $ 两个基站的距离为（ ）
A． $ 10\sqrt{6}\mathrm{k}\mathrm{m} $
B． $ 30(\sqrt{3}-1)\mathrm{k}\mathrm{m} $
C． $ 30(\sqrt{2}-1)\mathrm{k}\mathrm{m} $
D． $ 10\sqrt{5}\mathrm{k}\mathrm{m} $
在 $ △ACD $ 中, $ \mathrm{\angle }ADC={30}^{\circ } $ , $ \mathrm{\angle }ACD={120}^{\circ } $ ,所以 $ \mathrm{\angle }CAD={30}^{\circ } $ ,
所以 $ AC=CD=10\sqrt{3} $ .
又 $ \mathrm{\angle }ACB={75}^{\circ } $ ,所以 $ \mathrm{\angle }BCD={45}^{\circ } $ ,
在 $ △BDC $ 中, $ \mathrm{\angle }CDB={75}^{\circ } $ ， $ \mathrm{\angle }CBD={180}^{\circ }-({75}^{\circ }+{45}^{\circ })={60}^{\circ } $ ,由正弦定理,得 $ \dfrac{BC}{ \sin \mathrm{\angle }CDB}=\dfrac{CD}{ \sin \mathrm{\angle }CBD} $ ,则 $ BC=\dfrac{10\sqrt{3} \sin {75}^{\circ }}{ \sin {60}^{\circ }}=5\sqrt{2}+5\sqrt{6} $ .在 $ △ABC $ 中,由余弦定理,得
$ A{B}^{2}=A{C}^{2}+B{C}^{2}-2AC\cdot BC \cos \mathrm{\angle }ACB={\left(10\sqrt{3}\right) ^ {2}}+{\left(5\sqrt{2}+5\sqrt{6}\right) ^ {2}}-2×10\sqrt{3}×(5\sqrt{2}+5\sqrt{6})×\dfrac{\sqrt{6}-\sqrt{2}}{4}=500 $ ,所以 $ AB=10\sqrt{5} $ ,即 $ A $ , $ B $ 两个基站之间的距离为 $ 10\sqrt{5}\mathrm{k}\mathrm{m} $ .
故选 $ \mathrm{D} $ .
6．如图，南北分界线是蚌埠的标志性建筑，小明为了测量其高度 $ MN $ ，在地面上选择一个观测点 $ C $ ，在 $ C $ 处测得 $ A $ 处的无人机和该建筑的最高点 $ M $ 的仰角分别为 $ {30}^{\circ } $ , $ {45}^{\circ } $ ，无人机距地面的高度 $ AB $ 为20米，且在 $ A $ 处无人机测得点 $ M $ 的仰角为 $ {15}^{\circ } $ ，点 $ B $ ， $ C $ ， $ N $ 在同一条直线上，则该建筑的高度 $ MN $ （单位：米）为（ ）
A． $ 20\sqrt{3} $
B． $ 25\sqrt{3} $
C． $ \dfrac{40\sqrt{3}}{3} $
D．40
在 $ \mathrm{R}\mathrm{t}△ABC $ 中, $ \mathrm{\angle }ACB={30}^{\circ } $ , $ AB=20 $ ,则 $ AC=2AB=40 $ .
由题图可知 $ \mathrm{\angle }MAC={45}^{\circ } $ , $ \mathrm{\angle }MCA={180}^{\circ }-{45}^{\circ }-{30}^{\circ }={105}^{\circ } $ ,则 $ \mathrm{\angle }CMA={180}^{\circ }-{45}^{\circ }-{105}^{\circ }={30}^{\circ } $ .
在 $ △AMC $ 中,由正弦定理 $ \dfrac{AC}{ \sin \mathrm{\angle }AMC}=\dfrac{MC}{ \sin \mathrm{\angle }CAM} $ ,得 $ MC=\dfrac{40×\dfrac{\sqrt{2}}{2}}{\dfrac{1}{2}}=40\sqrt{2} $ .
在 $ \mathrm{R}\mathrm{t}△MNC $ 中, $ MN=MC\cdot \sin {45}^{\circ }=40\sqrt{2}×\dfrac{\sqrt{2}}{2}=40 $ .故选 $ \mathrm{D} $ .
7．某学生为测量宁波天封塔的高度，如图，选取了与天封塔底部 $ D $ 在同一水平面上的 $ A $ ， $ B $ 两点，测得 $ AB=50\sqrt{7} $ 米，在 $ A $ ， $ B $ 两点观察塔顶 $ C $ 点，仰角分别为 $ {45}^{\circ } $ 和 $ {30}^{\circ } $ ，且 $ \mathrm{\angle }ADB={150}^{\circ } $ ，则宁波天封塔的高度 $ CD $ （单位：米）是（ ）
A．50
B． $ 40\sqrt{3} $
C． $ 30\sqrt{7} $
D． $ 50\sqrt{7} $
设 $ CD=x $ ,由 $ \mathrm{\angle }CAD={45}^{\circ } $ , $ \mathrm{\angle }CBD={30}^{\circ } $ ,得 $ AD=x $ , $ BD=\sqrt{3}x $ .在 $ △ADB $ 中, $ \mathrm{\angle }ADB={150}^{\circ } $ ,由余弦定理得 $ (50\sqrt{7})^{2}={x}^{2}+ (\sqrt{3}x)^{2}-2x\cdot \sqrt{3}x\cdot (-\dfrac{\sqrt{3}}{2} ) $ ,解得 $ x=50 $ ,
所以宁波天封塔的高度 $ CD $ 是50米.故选 $ \mathrm{A} $ .
8．公路北侧有一幢楼，高为60米，公路与楼脚底面在同一水平面上.某人在点 $ A $ 处测得楼顶的仰角为 $ {45}^{\circ } $ ，他在公路上自西向东行走，行走60米到点 $ B $ 处，测得楼顶的仰角为 $ {45}^{\circ } $ ，沿该方向再行走60米到点 $ C $ 处，测得楼顶的仰角为 $ \theta $ ，则 $ \sin \theta $ 为（ ）
A． $ \dfrac{1}{2} $
B． $ \dfrac{\sqrt{2}}{2} $
C． $ \dfrac{\sqrt{3}}{3} $
D． $ \dfrac{1}{3} $
如图,记 $ DE $ 为楼的高度,由题意得 $ DE=AB=BC=60 $ , $ \mathrm{\angle }DAE=\mathrm{\angle }DBE={45}^{\circ } $ ,
则 $ AE=BE=AB=60 $ ,故 $ \mathrm{\angle }EAB={60}^{\circ } $ ,在 $ △ACE $ 中,由余弦定理得
$ EC=\sqrt{A{E}^{2}+A{C}^{2}-2AE\cdot AC \cos \mathrm{\angle }EAB}=\sqrt{{60}^{2}+{120}^{2}-2×60×120× \cos {60}^{\circ }}=60\sqrt{3} $ ,
在 $ \mathrm{R}\mathrm{t}△CDE $ 中, $ DC=\sqrt{{60}^{2}+(60\sqrt{3})^{2}}=120 $ ,则 $ \sin \theta = \sin \mathrm{\angle }DCE=\dfrac{DE}{DC}=\dfrac{1}{2} $ .故选 $ \mathrm{A} $ .
9．一艘渔船航行到 $ A $ 处时看灯塔 $ B $ 在 $ A $ 的南偏东 $ {15}^{\circ } $ 方向，距离为 $ 12\sqrt{6} $ 海里，灯塔 $ C $ 在 $ A $ 的北偏东 $ {60}^{\circ } $ 方向，距离为 $ 12\sqrt{3} $ 海里，该渔船由 $ A $ 处沿正东方向继续航行到 $ D $ 处时再看灯塔 $ B $ 在其南偏西 $ {30}^{\circ } $ 方向，则此时灯塔 $ C $ 位于渔船的（ ）
A．南偏东 $ {60}^{\circ } $ 方向
B．南偏西 $ {30}^{\circ } $ 方向
C．北偏西 $ {60}^{\circ } $ 方向
D．北偏西 $ {30}^{\circ } $ 方向
如图.
由题意，在 $ △ABD $ 中， $ B={15}^{\circ }+{30}^{\circ }={45}^{\circ } $ ， $ AB=12\sqrt{6} $ ， $ \mathrm{\angle }ADB={60}^{\circ } $ ，由正弦定理得 $ \dfrac{AD}{ \sin {45}^{\circ }}=\dfrac{AB}{ \sin {60}^{\circ }}=\dfrac{12\sqrt{6}}{\dfrac{\sqrt{3}}{2}}=24\sqrt{2} $ ，所以 $ AD=24 $ .
在 $ △ACD $ 中， $ AC=12\sqrt{3} $ ， $ \mathrm{\angle }CAD={30}^{\circ } $ ，由余弦定理得 $ C{D}^{2}=A{C}^{2}+A{D}^{2}-2AC×AD× \cos {30}^{\circ }={\left(12\sqrt{3}\right) ^ {2}}+{24}^{2}-2×12\sqrt{3}×24×\dfrac{\sqrt{3}}{2}=144 $ ，所以 $ CD=12 $ .
由正弦定理得 $ \dfrac{CD}{ \sin {30}^{\circ }}=\dfrac{AC}{ \sin \mathrm{\angle }CDA} $ ，
所以 $ \sin \mathrm{\angle }CDA=\dfrac{12\sqrt{3}×\dfrac{1}{2}}{12}=\dfrac{\sqrt{3}}{2} $ ，
又因为 $ AD > AC $ ，所以 $ \mathrm{\angle }CDA $ 为锐角，故 $ \mathrm{\angle }CDA={60}^{\circ } $ ，此时灯塔 $ C $ 位于渔船的北偏西 $ {30}^{\circ } $ 方向.故选 $ \mathrm{D} $ .
10．某校运动会开幕式上举行升旗仪式，旗杆正好处在坡角为 $ {15}^{\circ } $ 的观礼台的某一列的正前方，从这一列的第一排和最后一排测得旗杆顶部 $ B $ 的仰角分别为 $ {60}^{\circ } $ 和 $ {30}^{\circ } $ ，第一排和最后一排的距离为 $ 10\sqrt{6} $ 米（如图所示），旗杆底部与第一排在同一水平面上，若国歌播放的时间约为50秒，则升旗手匀速升旗的速度为 米/秒.
0.6
在 $ △BCD $ 中, $ \mathrm{\angle }BDC={30}^{\circ }+{15}^{\circ }={45}^{\circ } $ , $ \mathrm{\angle }CBD={180}^{\circ }-{45}^{\circ }-({180}^{\circ }-{15}^{\circ }-{60}^{\circ })={30}^{\circ } $ , $ CD=10\sqrt{6} $ ,
由正弦定理,得 $ \dfrac{BC}{ \sin \mathrm{\angle }BDC}=\dfrac{CD}{ \sin \mathrm{\angle }CBD} $ ,则 $ BC=\dfrac{CD \sin \mathrm{\angle }BDC}{ \sin \mathrm{\angle }CBD}=\dfrac{10\sqrt{6} \sin {45}^{\circ }}{ \sin {30}^{\circ }}=20\sqrt{3} $ .
在 $ \mathrm{R}\mathrm{t}△ABC $ 中, $ AB=BC \sin {60}^{\circ }=20\sqrt{3}×\dfrac{\sqrt{3}}{2}=30 $ .
所以升旗速度 $ v=\dfrac{AB}{t}=\dfrac{30}{50}=0.6 $ （米/秒）,
所以升旗手应以约0.6米/秒的速度匀速升旗.
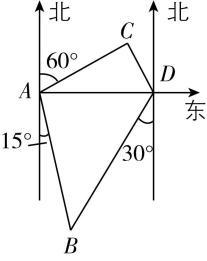
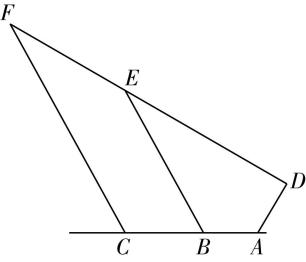
11．某海岸的 $ A $ 哨所在凌晨1点15分发现哨所北偏东 $ {30}^{\circ } $ 方向 $ 20\mathrm{n}\mathrm{m}\mathrm{i}\mathrm{l}\mathrm{e} $ 处的 $ D $ 点出现可疑船只，因天气恶劣能见度低，无法对船只进行识别，所以将该船雷达特征信号进行标记并上报周围哨所.早上5点15分位于 $ A $ 哨所正西方向 $ 20\mathrm{n}\mathrm{m}\mathrm{i}\mathrm{l}\mathrm{e} $ 的 $ B $ 哨所发现了该可疑船只位于 $ B $ 哨所北偏西 $ {30}^{\circ } $ 方向 $ 60\mathrm{n}\mathrm{m}\mathrm{i}\mathrm{l}\mathrm{e} $ 处的 $ E $ 点，并识别出其为走私船，立刻命令位于 $ B $ 哨所正西方向 $ 30\mathrm{n}\mathrm{m}\mathrm{i}\mathrm{l}\mathrm{e} $ 处 $ C $ 点的我方缉私船前往拦截，已知缉私船速度大小为 $ 30\mathrm{n}\mathrm{m}\mathrm{i}\mathrm{l}\mathrm{e}/\mathrm{h} $ .（假设所有船只均保持匀速直线航行）
（1） 求走私船的速度大小；
（2） 缉私船沿什么方向行驶才能截获走私船，并求出截获走私船的具体时间.
（1） 【解】如图,连接 $ BD $ , $ \because D $ 点位于 $ A $ 哨所北偏东 $ {30}^{\circ } $ 方向 $ 20\mathrm{n}\mathrm{m}\mathrm{i}\mathrm{l}\mathrm{e} $ 处, $ \therefore \mathrm{\angle }BAD={90}^{\circ }+{30}^{\circ }={120}^{\circ } $ , $ AD=20 $ , $ \because AB=20 $ ,
$ \therefore BD=\sqrt{A{D}^{2}+A{B}^{2}-2AD\cdot AB \cos {120}^{\circ }}=20\sqrt{3} $ .
$ \because AB=AD $ , $ \therefore \mathrm{\angle }ABD=\mathrm{\angle }ADB={30}^{\circ } $ .
$ \because E $ 点位于 $ B $ 哨所北偏西 $ {30}^{\circ } $ 方向 $ 60\mathrm{n}\mathrm{m}\mathrm{i}\mathrm{l}\mathrm{e} $ 处,
$ \therefore \mathrm{\angle }DBE={90}^{\circ }-{30}^{\circ }+{30}^{\circ }={90}^{\circ } $ , $ \therefore DE=\sqrt{B{D}^{2}+B{E}^{2}}=40\sqrt{3} $ .
设走私船的速度大小为 $ v\mathrm{n}\mathrm{m}\mathrm{i}\mathrm{l}\mathrm{e}/\mathrm{h} $ ,则 $ v=\dfrac{40\sqrt{3}}{4}=10\sqrt{3}(\mathrm{n}\mathrm{m}\mathrm{i}\mathrm{l}\mathrm{e}/\mathrm{h}) $ ,
$ \therefore $ 走私船的速度大小为 $ 10\sqrt{3}\mathrm{n}\mathrm{m}\mathrm{i}\mathrm{l}\mathrm{e}/\mathrm{h} $ .
（2） 连接 $ CE $ ,设在 $ F $ 点处截获走私船,截获走私船所需时间为 $ t\mathrm{h} $ .
$ \because BE=60 $ , $ BC=30 $ , $ \mathrm{\angle }CBE={60}^{\circ } $ ,
$ \therefore CE=\sqrt{B{E}^{2}+B{C}^{2}-2BE\cdot BC \cos {60}^{\circ }}=30\sqrt{3} $ .
$ \because B{E}^{2}=B{C}^{2}+C{E}^{2} $ , $ \therefore \mathrm{\angle }BCE={90}^{\circ } $ , $ \mathrm{\angle }BEC={30}^{\circ } $ ,
$ \therefore \mathrm{\angle }CEF={120}^{\circ } $ .
$ \because $ 走私船速度大小为 $ 10\sqrt{3}\mathrm{n}\mathrm{m}\mathrm{i}\mathrm{l}\mathrm{e}/\mathrm{h} $ ,缉私船速度大小为 $ 30\mathrm{n}\mathrm{m}\mathrm{i}\mathrm{l}\mathrm{e}/\mathrm{h} $ , $ \therefore EF=10\sqrt{3}t $ , $ CF=30t $ .
在 $ △CEF $ 中,根据余弦定理得, $ C{F}^{2}=C{E}^{2}+E{F}^{2}-2CE\cdot EF\cdot \cos {120}^{\circ } $ ,即 $ 900{t}^{2}=2700+300{t}^{2}-2×30\sqrt{3}×10\sqrt{3}t \cos {120}^{\circ } $ ,
化简得 $ 2{t}^{2}-3t-9=0 $ ,
$ \therefore t=-\dfrac{3}{2} $ （舍去）或 $ t=3 $ ,
此时 $ CE=EF=30\sqrt{3} $ ,
$ \therefore \mathrm{\angle }ECF={30}^{\circ } $ ,
$ \therefore $ 缉私船沿北偏西 $ {30}^{\circ } $ 方向行驶, $ 3\mathrm{h} $ 后即早上8点15分可截获走私船．
12．如图，计划在两个山顶 $ M $ ， $ N $ 间架设一条索道.为测量 $ M $ ， $ N $ 间的距离，施工单位测得以下数据：两个山顶的海拔高 $ MC=100\sqrt{3}\mathrm{m} $ ， $ NB=50\sqrt{2}\mathrm{m} $ ，在 $ BC $ 同一水平面上选一点 $ A $ ，在 $ A $ 处测得山顶 $ M $ ， $ N $ 的仰角分别为 $ {60}^{\circ } $ 和 $ {30}^{\circ } $ ，且测得 $ \mathrm{\angle }MAN={45}^{\circ } $ ，则 $ M $ ， $ N $ 间的距离为 .
$ 100\sqrt{2}\mathrm{m} $
在 $ \mathrm{R}\mathrm{t}△MCA $ 中, $ \mathrm{\angle }MAC={60}^{\circ } $ , $ MC=100\sqrt{3} $ ,
则 $ MA=\dfrac{MC}{ \sin {60}^{\circ }}=\dfrac{100\sqrt{3}}{\dfrac{\sqrt{3}}{2}}=200 $ .
在 $ \mathrm{R}\mathrm{t}△NBA $ 中, $ \mathrm{\angle }NAB={30}^{\circ } $ , $ NB=50\sqrt{2} $ ,
则 $ NA=\dfrac{NB}{ \sin {30}^{\circ }}=\dfrac{50\sqrt{2}}{\dfrac{1}{2}}=100\sqrt{2} $ .
在 $ △MAN $ 中, $ MA=200 $ , $ NA=100\sqrt{2} $ , $ \mathrm{\angle }MAN={45}^{\circ } $ ,
由余弦定理得 $ M{N}^{2}=M{A}^{2}+N{A}^{2}-2MA\cdot NA\cdot \cos \mathrm{\angle }MAN={200}^{2}+(100\sqrt{2})^{2}-2×200×100\sqrt{2}× \cos {45}^{\circ }=20000 $ ,
所以 $ MN=\sqrt{20000}=100\sqrt{2} $ ,
所以 $ M $ , $ N $ 间的距离为 $ 100\sqrt{2}\mathrm{m} $ .