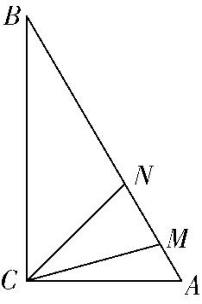
11.为响应国家“乡村振兴”号召,农民老王拟将自家一块直角三角形地按如图规划成3个功能区: $ △BNC $ 区域规划为荔枝林, $ △CMA $ 区域规划为供游客住宿及餐饮的民宿, $ △MNC $ 区域规划为供休闲垂钓的小型鱼塘.为安全起见,在鱼塘 $ △MNC $ 周围筑起护栏.已知 $ AC=40\mathrm{m} $ , $ BC=40\sqrt{3}\mathrm{m} $ , $ AC\perp BC $ , $ \mathrm{\angle }MCN={30}^{\circ } $ .
(1) 若鱼塘 $ △MNC $ 的面积是民宿 $ △CMA $ 的面积的 $ \sqrt{3} $ 倍,求 $ \mathrm{\angle }ACM $ .
答案:(1) 【解】设 $ \mathrm{\angle }ACM=\theta ({0}^{\circ } < \theta < {60}^{\circ }) $ ,则 $ \mathrm{\angle }BCN={60}^{\circ }-\theta $ ,
在 $ △ABC $ 中, $ AC\perp BC $ , $ AC=40 $ , $ BC=40\sqrt{3} $ ,则 $ A={60}^{\circ } $ , $ B={30}^{\circ } $ .
因为鱼塘 $ △MNC $ 的面积是民宿 $ △CMA $ 的面积的 $ \sqrt{3} $ 倍,
所以 $ \dfrac{1}{2}CN\cdot CM \sin {30}^{\circ }=\sqrt{3}\cdot \dfrac{1}{2}AC\cdot CM \sin \theta $ ,即 $ CN=80\sqrt{3} \sin \theta $ .
在 $ △CAN $ 中, $ \mathrm{\angle }CNA=B+\mathrm{\angle }BCN={90}^{\circ }-\theta $ ,由正弦定理可得 $ \dfrac{CN}{ \sin A}=\dfrac{AC}{ \sin \mathrm{\angle }CNA} $ ,即 $ \dfrac{CN}{ \sin {60}^{\circ }}=\dfrac{AC}{ \sin ({90}^{\circ }-\theta )}=\dfrac{40}{ \cos \theta } $ ,则 $ CN=\dfrac{20\sqrt{3}}{ \cos \theta } $ ,则 $ 80\sqrt{3} \sin \theta =\dfrac{20\sqrt{3}}{ \cos \theta } $ ,即 $ \sin 2\theta =\dfrac{1}{2} $ .
由 $ {0}^{\circ } < 2\theta < {120}^{\circ } $ ,得 $ 2\theta ={30}^{\circ } $ ,
所以 $ \theta ={15}^{\circ } $ ,即 $ \mathrm{\angle }ACM={15}^{\circ } $ .
(2) 由(1)知 $ \mathrm{\angle }ACM=\theta ({0}^{\circ } < \theta < {60}^{\circ }) $ , $ B={30}^{\circ } $ , $ A={60}^{\circ } $ ,所以 $ AB=2AC=80 $ ,
在 $ △ACM $ 中,由正弦定理得 $ \dfrac{CM}{ \sin A}=\dfrac{AC}{ \sin \mathrm{\angle }AMC} $ ,即 $ \dfrac{CM}{ \sin {60}^{\circ }}=\dfrac{AC}{ \sin ({120}^{\circ }-\theta )} $ ,则 $ CM=\dfrac{20\sqrt{3}}{ \sin ({120}^{\circ }-\theta )} $ ,由(1)知 $ CN=\dfrac{20\sqrt{3}}{ \cos \theta } $ ,
所以 $ {S}_{△CMN}=\dfrac{1}{2}CM\cdot CN\cdot \sin {30}^{\circ } $
$ =\dfrac{300}{ \sin ({120}^{\circ }-\theta ) \cos \theta } $
$ =\dfrac{300}{\dfrac{1}{2} \sin \theta \cos \theta +\dfrac{\sqrt{3}}{2}{ \cos }^{2}\theta } $
$ =\dfrac{600}{\dfrac{ \sin 2\theta }{2}+\dfrac{\sqrt{3} \cos 2\theta }{2}+\dfrac{\sqrt{3}}{2}} $
$ =\dfrac{1200}{2 \sin (2\theta +{60}^{\circ })+\sqrt{3}} $ .
又 $ {0}^{\circ } < \theta < {60}^{\circ } $ ,所以 $ {60}^{\circ } < 2\theta +{60}^{\circ } < {180}^{\circ } $ ,所以当且仅当 $ 2\theta +{60}^{\circ }={90}^{\circ } $ ,即 $ \theta ={15}^{\circ } $ 时,
$ △CMN $ 的面积取最小值,为 $ \dfrac{1200}{2+\sqrt{3}}=1200(2-\sqrt{3}){\mathrm{m}}^{2} $ .

 (多选)
(多选)