1．在 $ △ABC $ 中，已知 $ AC=5 $ , $ AB=3 $ , $ BC=7 $ , $ AD $ 是 $ BC $ 边上的中线，则 $ AD= $ （ ）
A． $ \dfrac{15}{4} $
B． $ \dfrac{\sqrt{19}}{2} $
C． $ \dfrac{7}{2} $
D． $ \dfrac{15}{7} $
在 $ △ABC $ 中,由余弦定理,得 $ \cos B=\dfrac{A{B}^{2}+B{C}^{2}-A{C}^{2}}{2AB\cdot BC}=\dfrac{9+49-25}{2×3×7}=\dfrac{11}{14} $ .
在 $ △ABD $ 中,由余弦定理,得 $ A{D}^{2}=A{B}^{2}+B{D}^{2}-2AB\cdot BD \cos B=9+\dfrac{49}{4}-2×3×\dfrac{7}{2}×\dfrac{11}{14}=\dfrac{19}{4} $ ,则 $ AD=\dfrac{\sqrt{19}}{2} $ .故选 $ \mathrm{B} $ .
2．在 $ △ABC $ 中，内角 $ A $ ， $ B $ ， $ C $ 的对边分别为 $ a $ ， $ b $ ， $ c $ ，向量 $ \boldsymbol{m}=(b,c) $ ， $ \boldsymbol{n}=( \cos B, \sin C) $ ， $ \boldsymbol{m}//\boldsymbol{n} $ .若 $ c=\sqrt{3} $ ， $ a=\sqrt{6} $ ， $ BD $ 为 $ AC $ 边上的中线，则 $ BD= $ （ ）
A． $ \dfrac{\sqrt{6}}{2} $
B．3
C． $ \dfrac{\sqrt{15}}{2} $
D． $ \dfrac{\sqrt{10}}{2} $
因为 $ \boldsymbol{m}=(b,c) $ , $ \boldsymbol{n}=( \cos B, \sin C) $ , $ \boldsymbol{m}//\boldsymbol{n} $ ,所以 $ b \sin C=c \cos B $ ,结合正弦定理得 $ \sin B \sin C= \sin C \cos B $ .
因为 $ C\in (0,\mathrm{\pi }) $ ,所以 $ \sin C\ne 0 $ ,所以 $ \sin B= \cos B $ .
若 $ \cos B=0 $ ,则 $ \sin B=±1 $ ,与上式矛盾,故 $ \cos B\ne 0 $ ,则 $ \tan B=1 $ ,
因为 $ B\in (0,\mathrm{\pi }) $ ,所以 $ B=\dfrac{\mathrm{\pi }}{4} $ .
由 $ BD $ 为 $ AC $ 边上的中线,得 $ 2\overrightarrow {BD}=\overrightarrow {BC}+\overrightarrow {BA} $ ,
则 $ 4{\overrightarrow {BD}}^{2}=(\overrightarrow {BC}+\overrightarrow {BA})^{2}={\overrightarrow {BC}}^{2}+2\overrightarrow {BC}\cdot \overrightarrow {BA}+{\overrightarrow {BA}}^{2}={a}^{2}+2ac \cos \mathrm{\angle }ABC+{c}^{2}=6+2×\sqrt{6}×\sqrt{3}×\dfrac{\sqrt{2}}{2}+3=15 $ ,得 $ BD=\dfrac{\sqrt{15}}{2} $ .故选 $ \mathrm{C} $ .
3．在锐角三角形 $ ABC $ 中，内角 $ A $ ， $ B $ ， $ C $ 所对的边分别为 $ a $ ， $ b $ ， $ c $ ，已知 $ C=\dfrac{\mathrm{\pi }}{3} $ , $ c=4 $ ， $ D $ 为 $ AB $ 的中点，则中线 $ CD $ 的取值范围是（ ）
A． $ (2,2\sqrt{3}] $
B． $ (\dfrac{4\sqrt{3}}{3},2\sqrt{3}] $
C． $ (\dfrac{2\sqrt{21}}{3},2\sqrt{3}] $
D． $ (\dfrac{4\sqrt{3}}{3},\dfrac{2\sqrt{21}}{3}] $
由 $ CD $ 是边 $ AB $ 上的中线,得 $ \overrightarrow {CD}=\dfrac{1}{2}(\overrightarrow {CA}+\overrightarrow {CB}) $ ,
则 $ {\overrightarrow {CD}}^{2}=\dfrac{1}{4}({\overrightarrow {CA}}^{2}+{\overrightarrow {CB}}^{2}+2\overrightarrow {CA}\cdot \overrightarrow {CB})=\dfrac{1}{4}({b}^{2}+{a}^{2}+2ba \cos \dfrac{\mathrm{\pi }}{3})=\dfrac{1}{4}({a}^{2}+{b}^{2}+ab) $ .
由正弦定理得 $ \dfrac{a}{ \sin A}=\dfrac{b}{ \sin B}=\dfrac{c}{ \sin C}=\dfrac{4}{ \sin \dfrac{\mathrm{\pi }}{3}}=\dfrac{8\sqrt{3}}{3} $ ,得 $ a=\dfrac{8\sqrt{3}}{3} \sin A $ , $ b=\dfrac{8\sqrt{3}}{3} \sin B $ ,则 $ {\overrightarrow {CD}}^{2}=\dfrac{1}{4}(\dfrac{64}{3}{ \sin }^{2}A+\dfrac{64}{3}{ \sin }^{2}B+\dfrac{64}{3} \sin A \sin B)=\dfrac{16}{3}({ \sin }^{2}A+{ \sin }^{2}B+ \sin A \sin B). $
而 $ { \sin }^{2}B={ \sin }^{2} (A+C )= (\dfrac{\sqrt{3}}{2} \cos A+\dfrac{1}{2} \sin A)^{2}=\dfrac{3}{4}{ \cos }^{2}A+\dfrac{\sqrt{3}}{2} \sin A \cos A+\dfrac{1}{4}{ \sin }^{2}A $ ,
$ \sin A \sin B= \sin A \sin (A+C)= \sin A\cdot (\dfrac{\sqrt{3}}{2} \cos A+\dfrac{1}{2} \sin A)=\dfrac{\sqrt{3}}{2} \sin A \cos A+\dfrac{1}{2}{ \sin }^{2}A $ ,
于是 $ {\overrightarrow {CD}}^{2}=\dfrac{16}{3}({ \sin }^{2}A+\dfrac{3}{4}{ \cos }^{2}A+\dfrac{\sqrt{3}}{2}\cdot \sin A \cos A+\dfrac{1}{4}{ \sin }^{2}A+\dfrac{\sqrt{3}}{2} \sin A \cos A+\dfrac{1}{2}{ \sin }^{2}A) $
$ =\dfrac{16}{3}({ \sin }^{2}A+\sqrt{3} \sin A \cos A+\dfrac{3}{4}) $
$ =\dfrac{8}{3}(1- \cos 2A)+\dfrac{8\sqrt{3}}{3} \sin 2A+4=\dfrac{16}{3}\cdot \sin (2A-\dfrac{\mathrm{\pi }}{6})+\dfrac{20}{3} $ ,
由 $ △ABC $ 为锐角三角形, $ C=\dfrac{\mathrm{\pi }}{3} $ ,得 $ \begin{cases}0 < \dfrac{2\mathrm{\pi }}{3}-A < \dfrac{\mathrm{\pi }}{2},\\ 0 < A < \dfrac{\mathrm{\pi }}{2},\end{cases} $ 即 $ \dfrac{\mathrm{\pi }}{6} < A < \dfrac{\mathrm{\pi }}{2} $ ,
则 $ \dfrac{\mathrm{\pi }}{6} < 2A-\dfrac{\mathrm{\pi }}{6} < \dfrac{5\mathrm{\pi }}{6} $ ,所以 $ \dfrac{1}{2} < \sin (2A-\dfrac{\mathrm{\pi }}{6})\leqslant 1 $ ,因此 $ \dfrac{28}{3} < {\overrightarrow {CD}}^{2}\leqslant 12 $ ,即 $ \dfrac{2\sqrt{21}}{3} < |\overrightarrow {CD}|\leqslant 2\sqrt{3} $ ,
所以 $ CD $ 的取值范围为 $ (\dfrac{2\sqrt{21}}{3},2\sqrt{3}] $ .故选 $ \mathrm{C} $ .
4．在 $ △ABC $ 中，内角 $ A $ ， $ B $ ， $ C $ 对应的边分别是 $ a $ ， $ b $ ， $ c $ ，且 $ b \cos C+c \cos B=2a \cos A $ .
（1） 求角 $ A $ ；
（2） 若 $ AB $ 的长为 $ {\rm 3，} AC $ 边上的中线 $ BD $ 长为 $ \sqrt{7} $ ，求 $ △ABC $ 的周长.
（1） 【解】因为 $ b \cos C+c \cos B=2a \cos A $ ,
所以由正弦定理得 $ \sin B \cos C+ \sin C \cos B=2 \sin A \cos A $ ,即 $ \sin A=2 \sin A \cos A. $
因为 $ 0 < A < \mathrm{\pi } $ ,所以 $ \sin A\ne 0 $ ,
所以 $ \cos A=\dfrac{1}{2} $ ,所以 $ A=\dfrac{\mathrm{\pi }}{3} $ .
（2） 在 $ △ABD $ 中, $ AB=3 $ , $ BD=\sqrt{7} $ ,
由余弦定理得 $ A{B}^{2}+A{D}^{2}-B{D}^{2}=2AB\cdot AD\cdot \cos A $ ,即 $ 9+A{D}^{2}-7=2×3×AD×\dfrac{1}{2} $ ,
解得 $ AD=1 $ 或 $ AD=2 $ .
当 $ AD=1 $ 时, $ AC=2AD=2 $ ,
则 $ B{C}^{2}=A{B}^{2}+A{C}^{2}-2AB\cdot AC\cdot \cos A=7 $ ,即 $ BC=\sqrt{7} $ ,此时 $ △ABC $ 的周长为 $ 5+\sqrt{7} $ ；
当 $ AD=2 $ 时, $ AC=2AD=4 $ ,
则 $ B{C}^{2}=A{B}^{2}+A{C}^{2}-2AB\cdot AC\cdot \cos A=13 $ ,即 $ BC=\sqrt{13} $ ,此时 $ △ABC $ 的周长为 $ 7+\sqrt{13} $ .
综上所述, $ △ABC $ 的周长为 $ 5+\sqrt{7} $ 或 $ 7+\sqrt{13} $ .
5．已知 $ △ABC $ 的内角 $ A $ ， $ B $ ， $ C $ 的对边分别为 $ a $ ， $ b $ ， $ c $ ，且 $ a=1 $ ， $ \sqrt{3} \cos C=c \sin A $ .若 $ b=3 $ ， $ D $ 是 $ AB $ 上的点， $ CD $ 平分 $ \mathrm{\angle }ACB $ ，则 $ △ACD $ 的面积为（ ）
A． $ \dfrac{9\sqrt{3}}{32} $
B． $ \dfrac{9\sqrt{3}}{16} $
C． $ \dfrac{9\sqrt{3}}{4} $
D． $ \dfrac{9\sqrt{3}}{2} $
由正弦定理可知, $ \dfrac{a}{ \sin A}=\dfrac{c}{ \sin \mathrm{\angle }ACB} $ ,即 $ a \sin \mathrm{\angle }ACB=c \sin A $ ,
故 $ \sqrt{3} \cos \mathrm{\angle }ACB=c \sin A=a \sin \mathrm{\angle }ACB= \sin \mathrm{\angle }ACB $ ,故 $ \tan \mathrm{\angle }ACB=\sqrt{3} $ ,而 $ \mathrm{\angle }ACB\in (0,\mathrm{\pi }) $ ,故 $ \mathrm{\angle }ACB=\dfrac{\mathrm{\pi }}{3} $ .
因为 $ D $ 是 $ AB $ 上的点, $ CD $ 平分 $ \mathrm{\angle }ACB $ ,所以由角平分线定理可知, $ \dfrac{AD}{BD}=\dfrac{AC}{BC}=\dfrac{b}{a}=3 $ ,故 $ AD=\dfrac{3}{4}AB $ ,即 $ {S}_{△ACD}=\dfrac{3}{4}\cdot {S}_{△ABC}=\dfrac{3}{4}×\dfrac{1}{2}ab\cdot \sin \mathrm{\angle }ACB=\dfrac{3}{4}×\dfrac{1}{2}×1×3× \sin \dfrac{\mathrm{\pi }}{3}=\dfrac{9\sqrt{3}}{16} $ .故选 $ \mathrm{B} $ .
6．在 $ △ABC $ 中，点 $ M $ ， $ N $ 在边 $ BC $ 上， $ AM $ 为边 $ BC $ 上的中线， $ AN $ 为 $ \mathrm{\angle }BAC $ 的平分线.若 $ \mathrm{\angle }BAC=\dfrac{\mathrm{\pi }}{3} $ ， $ AM=\dfrac{\sqrt{21}}{2} $ ， $ △ABC $ 的面积等于 $ \sqrt{3} $ ，则 $ AN= $ （ ）
A． $ \dfrac{2}{5} $
B． $ \dfrac{2\sqrt{3}}{5} $
C． $ \dfrac{4}{5} $
D． $ \dfrac{4\sqrt{3}}{5} $
记 $ △ABC $ 的内角 $ A $ , $ B $ , $ C $ 所对的边分别为 $ a $ , $ b $ , $ c.\because AM $ 为边 $ BC $ 上的中线, $ \therefore 2\overrightarrow {AM}=\overrightarrow {AB}+\overrightarrow {AC} $ ,
即 $ 4|\overrightarrow {AM}{|}^{2}=|\overrightarrow {AB}{|}^{2}+|\overrightarrow {AC}{|}^{2}+2\overrightarrow {AB}\cdot \overrightarrow {AC} $ ,即 $ 4×\dfrac{21}{4}={c}^{2}+{b}^{2}+2cb×\dfrac{1}{2} $ ,
即 $ {c}^{2}+{b}^{2}+bc=21 $ , $ \therefore (b+c)^{2}=21+bc $ .
$ \because {S}_{△ABC}=\dfrac{1}{2}bc \sin \mathrm{\angle }BAC=\dfrac{\sqrt{3}}{4}bc=\sqrt{3} $ ,
$ \therefore bc=4 $ , $ \therefore (b+c)^{2}=21+4=25 $ , $ \therefore b+c=5 $ .
$ \because AN $ 为 $ \mathrm{\angle }BAC $ 的平分线, $ \mathrm{\angle }BAC=\dfrac{\mathrm{\pi }}{3} $ ,
$ \therefore \mathrm{\angle }BAN=\mathrm{\angle }CAN=\dfrac{\mathrm{\pi }}{6} $ .
又 $ \because {S}_{△ABN}+{S}_{△ACN}={S}_{△ABC} $ ,
$ \therefore \dfrac{1}{2}×c×AN× \sin \dfrac{\mathrm{\pi }}{6}+\dfrac{1}{2}×b×AN× \sin \dfrac{\mathrm{\pi }}{6}=\sqrt{3} $ ,
即 $ \dfrac{1}{4}×AN×(b+c)=\sqrt{3} $ ,
$ \therefore \dfrac{1}{4}×AN×5=\sqrt{3} $ ,
解得 $ AN=\dfrac{4\sqrt{3}}{5} $ .故选 $ \mathrm{D} $ .
7．已知 $ △ABC $ 的内角 $ A $ ， $ B $ ， $ C $ 的对边分别为 $ a $ ， $ b $ ， $ c $ ，且 $ \dfrac{ \sin A- \sin B}{ \sin C}=\dfrac{c-b}{a+b} $ .
（1） 求角 $ A $ .
（2） 已知 $ △ABC $ 的面积为 $ 4\sqrt{3} $ .
① 当 $ E $ 为 $ BC $ 的中点，且 $ b+c=10 $ 时，求 $ BC $ 边上的中线 $ AE $ 的长；
② 当 $ D $ 为边 $ BC $ 上的点，且 $ AD $ 平分 $ \mathrm{\angle }BAC $ 时，求 $ AD $ 的最大值.
（1） 【解】由 $ \dfrac{ \sin A- \sin B}{ \sin C}=\dfrac{c-b}{a+b} $ 及正弦定理得 $ \dfrac{a-b}{c}=\dfrac{c-b}{a+b} $ ,即 $ {a}^{2}={b}^{2}+{c}^{2}-bc $ .
由余弦定理得 $ \cos A=\dfrac{{b}^{2}+{c}^{2}-{a}^{2}}{2bc}=\dfrac{1}{2} $ .
因为 $ 0 < A < \mathrm{\pi } $ ,所以 $ A=\dfrac{\mathrm{\pi }}{3} $ .
（2） ① 由 $ \dfrac{1}{2}bc \sin \mathrm{\angle }BAC=4\sqrt{3} $ ,得 $ bc=16 $ .又 $ b+c=10 $ ,所以 $ {b}^{2}+{c}^{2}=(b+c)^{2}-2bc={10}^{2}-2×16=68 $ .
因为 $ \overrightarrow {AE}=\dfrac{1}{2}(\overrightarrow {AB}+\overrightarrow {AC}) $ ,所以 $ {\overrightarrow {AE}}^{2}=\dfrac{1}{4}({\overrightarrow {AB}}^{2}+2\overrightarrow {AB}\cdot \overrightarrow {AC}+{\overrightarrow {AC}}^{2})=\dfrac{1}{4}({c}^{2}+2bc\cdot \cos \dfrac{\mathrm{\pi }}{3}+{b}^{2})=21 $ ,
所以 $ AE=\sqrt{21} $ .
② 由以上可知, $ \mathrm{\angle }BAC=\dfrac{\mathrm{\pi }}{3} $ , $ bc=16 $ .
由 $ {S}_{△ADB}+{S}_{△ADC}={S}_{△ABC} $ ,得 $ \dfrac{1}{2}AD\cdot c\cdot \sin \dfrac{\mathrm{\pi }}{6}+\dfrac{1}{2}AD\cdot b\cdot \sin \dfrac{\mathrm{\pi }}{6}=\dfrac{1}{2}bc \sin \dfrac{\mathrm{\pi }}{3} $ ,
解得 $ AD=\dfrac{16\sqrt{3}}{b+c} $ .由于 $ b+c\geqslant 2\sqrt{bc}=8 $ ,当且仅当 $ b=c=4 $ 时取等号,故 $ AD\leqslant 2\sqrt{3} $ .
故 $ AD $ 的最大值为 $ 2\sqrt{3} $ .
8．已知 $ △ABC $ 的内角 $ A $ ， $ B $ ， $ C $ 的对边分别为 $ a $ ， $ b $ ， $ c $ ，且 $ B=\dfrac{\mathrm{\pi }}{4} $ ， $ a=2\sqrt{2} $ ， $ b=2\sqrt{5} $ ，则 $ AC $ 边上的高 $ ℎ= $ （ ）
A． $ \dfrac{3\sqrt{2}}{2} $
B． $ \dfrac{6\sqrt{5}}{5} $
C． $ \dfrac{5\sqrt{3}}{6} $
D． $ \dfrac{7\sqrt{6}}{8} $
$ \because B=\dfrac{\mathrm{\pi }}{4} $ , $ a=2\sqrt{2} $ , $ b=2\sqrt{5} $ ,
$ \therefore $ 由余弦定理得 $ \cos B=\dfrac{{a}^{2}+{c}^{2}-{b}^{2}}{2ac} $ ,
即 $ \dfrac{\sqrt{2}}{2}=\dfrac{{\left(2\sqrt{2}\right) ^ {2}}+{c}^{2}-{\left(2\sqrt{5}\right) ^ {2}}}{2×2\sqrt{2}×c} $ ,
解得 $ c=6 $ 或 $ c=-2 $ （舍去）.
由三角形的面积公式可得 $ {S}_{△ABC}=\dfrac{1}{2}bℎ=\dfrac{1}{2}ac \sin B $ ,即 $ ℎ=\dfrac{ac \sin B}{b}=\dfrac{6\sqrt{5}}{5} $ .故选 $ \mathrm{B} $ .
9．在 $ △ABC $ 中，内角 $ A $ , $ B $ , $ C $ 所对的边分别是 $ a $ , $ b $ , $ c $ .若 $ a \cos B+b \cos A=4 $ ， $ AB $ 边上的高为 $ 2\sqrt{3} $ ，则角 $ C $ 的最大值为（ ）
A． $ \dfrac{\mathrm{\pi }}{4} $
B． $ \dfrac{\mathrm{\pi }}{3} $
C． $ \dfrac{5\mathrm{\pi }}{12} $
D． $ \dfrac{7\mathrm{\pi }}{12} $
由余弦定理得 $ a \cos B+b \cos A=\dfrac{{a}^{2}+{c}^{2}-{b}^{2}}{2c}+\dfrac{{b}^{2}+{c}^{2}-{a}^{2}}{2c}=c=4 $ ,
又 $ AB $ 边上的高为 $ 2\sqrt{3} $ ,
$ \therefore {S}_{△ABC}=\dfrac{1}{2}×4×2\sqrt{3}=\dfrac{1}{2}ab \sin C $ ,即 $ ab=\dfrac{8\sqrt{3}}{ \sin C} $ .
$ \because \cos C=\dfrac{{a}^{2}+{b}^{2}-{c}^{2}}{2ab}\geqslant \dfrac{2ab-{c}^{2}}{2ab}=1-\dfrac{8}{ab} $ ,当且仅当 $ a=b $ 时取等号,
$ \therefore \cos C\geqslant 1-\dfrac{\sqrt{3}}{3} \sin C $ ,即 $ \dfrac{1}{2} \sin C+\dfrac{\sqrt{3}}{2} \cos C\geqslant \dfrac{\sqrt{3}}{2} $ ,即 $ \sin (C+\dfrac{\mathrm{\pi }}{3})\geqslant \dfrac{\sqrt{3}}{2}① $ .
$ \because C\in (0,\mathrm{\pi }) $ , $ \therefore C+\dfrac{\mathrm{\pi }}{3}\in (\dfrac{\mathrm{\pi }}{3},\dfrac{4\mathrm{\pi }}{3}) $ ,结合①可得 $ C+\dfrac{\mathrm{\pi }}{3}\in (\dfrac{\mathrm{\pi }}{3},\dfrac{2\mathrm{\pi }}{3}] $ ,
$ \therefore C\in (0,\dfrac{\mathrm{\pi }}{3}] $ ,故角 $ C $ 的最大值为 $ \dfrac{\mathrm{\pi }}{3} $ .故选 $ \mathrm{B} $ .
10．在 $ △ABC $ 中，内角 $ A $ , $ B $ , $ C $ 所对的边分别是 $ a $ , $ b $ , $ c $ ，且 $ a \cos C+\sqrt{3}a \sin C-b-c=0 $ .
（1） 求 $ A $ 的大小；
（2） 若 $ AC $ 边的中线为 $ BE $ , $ BE=\dfrac{\sqrt{7}}{2}c $ , $ b=6 $ ，求 $ BC $ 边上的高.
（1） 【解】因为 $ a \cos C+\sqrt{3}a \sin C-b-c=0 $ ,所以由正弦定理得 $ \sin A \cos C+\sqrt{3} \sin A \sin C- \sin B- \sin C=0 $ .
又 $ A+B+C=\mathrm{\pi } $ ,则 $ \sin B= \sin (\mathrm{\pi }-A-C)= \sin (A+C) $ ,
所以 $ \sin A \cos C+\sqrt{3} \sin A \sin C- \sin (A+C)- \sin C=0 $ ,
所以 $ \sqrt{3} \sin A \sin C- \cos A \sin C- \sin C=0 $ .又 $ C\in (0,\mathrm{\pi }) $ ,则 $ \sin C\ne 0 $ ,
可得 $ \sqrt{3} \sin A- \cos A=1 $ ,
即 $ \sin (A-\dfrac{\mathrm{\pi }}{6})=\dfrac{1}{2} $ .
因为 $ A\in (0,\mathrm{\pi }) $ ,所以 $ A-\dfrac{\mathrm{\pi }}{6}\in (-\dfrac{\mathrm{\pi }}{6},\dfrac{5\mathrm{\pi }}{6}) $ ,所以 $ A-\dfrac{\mathrm{\pi }}{6}=\dfrac{\mathrm{\pi }}{6} $ ,所以 $ A=\dfrac{\mathrm{\pi }}{3} $ .
（2） 在 $ △ABE $ 中, $ B{E}^{2}=A{B}^{2}+A{E}^{2}-2AB\cdot AE\cdot \cos A $ ,即 $ \dfrac{7}{4}{c}^{2}={c}^{2}+9-3c $ ,解得 $ c=2 $ （负值舍去）.
又 $ {a}^{2}={b}^{2}+{c}^{2}-2bc \cos A=28 $ ,解得 $ a=2\sqrt{7} $ .
设 $ BC $ 边上的高为 $ ℎ $ ,
因为 $ {S}_{△ABC}=\dfrac{1}{2}bc \sin A=\dfrac{1}{2}aℎ $ ,
所以 $ \dfrac{1}{2}×6×2×\dfrac{\sqrt{3}}{2}=\dfrac{1}{2}×2\sqrt{7}\cdot ℎ $ ,可得 $ BC $ 边上的高 $ ℎ=\dfrac{3\sqrt{21}}{7} $ .
11．如图，在 $ △ABC $ 中，已知 $ B={45}^{\circ } $ ， $ D $ 是 $ BC $ 边上的一点， $ AD=5 $ ， $ AC=7 $ ， $ DC=3 $ ，则 $ AB= $ （ ）
A． $ 4\sqrt{3} $
B． $ 5\sqrt{2} $
C． $ 2\sqrt{10} $
D． $ \dfrac{5\sqrt{6}}{2} $
在 $ △ACD $ 中,由余弦定理得 $ \cos C=\dfrac{A{C}^{2}+C{D}^{2}-A{D}^{2}}{2AC\cdot CD}=\dfrac{49+9-25}{2×7×3}=\dfrac{11}{14} $ ,
又因为 $ C\in (0,\mathrm{\pi }) $ ,所以 $ \sin C=\sqrt{1-{\left(\dfrac{11}{14}\right) ^ {2}}}=\dfrac{5\sqrt{3}}{14} $ .
在 $ △ABC $ 中,由正弦定理得 $ \dfrac{AB}{ \sin C}=\dfrac{AC}{ \sin B} $ ,即 $ \dfrac{AB}{\dfrac{5\sqrt{3}}{14}}=\dfrac{7}{\dfrac{\sqrt{2}}{2}} $ ,解得 $ AB=\dfrac{5\sqrt{6}}{2} $ .故选 $ \mathrm{D} $ .
12．如图，在四边形 $ ABCD $ 中， $ \mathrm{\angle }ADB=\mathrm{\angle }DCA={45}^{\circ } $ ， $ \mathrm{\angle }BDC={30}^{\circ } $ ， $ \mathrm{\angle }BCA={15}^{\circ } $ ， $ AB=5\sqrt{5} $ ，则 $ CD $ 的长为（ ）
A． $ 5\sqrt{3} $
B． $ 5\sqrt{5} $
C． $ 10\sqrt{3} $
D． $ 10\sqrt{5} $
因为 $ \mathrm{\angle }BDC={30}^{\circ } $ , $ \mathrm{\angle }BCD={15}^{\circ }+{45}^{\circ }={60}^{\circ } $ ,所以 $ \mathrm{\angle }CBD={90}^{\circ } $ ,
设 $ BC=x $ ,则 $ CD=2x $ , $ BD=\sqrt{3}x $ ,
在 $ △ACD $ 中, $ \mathrm{\angle }DCA={45}^{\circ } $ , $ \mathrm{\angle }ADC={30}^{\circ }+{45}^{\circ }={75}^{\circ } $ ,故 $ \mathrm{\angle }CAD={60}^{\circ } $ ,
由正弦定理可得 $ \dfrac{AD}{ \sin \mathrm{\angle }DCA}=\dfrac{CD}{ \sin \mathrm{\angle }CAD} $ ,则 $ AD=\dfrac{CD \sin {45}^{\circ }}{ \sin {60}^{\circ }}=\dfrac{2\sqrt{6}}{3}x $ ,
在 $ △ABD $ 中,由余弦定理可得 $ A{B}^{2}=A{D}^{2}+B{D}^{2}-2AD\cdot BD \cos {45}^{\circ } $ ,
即 $ \dfrac{8}{3}{x}^{2}+3{x}^{2}-2\cdot \dfrac{2\sqrt{6}}{3}x\cdot \sqrt{3}x\cdot \dfrac{\sqrt{2}}{2}=\dfrac{5}{3}{x}^{2}=125 $ ,解得 $ x=5\sqrt{3} $ ,故 $ CD=2x=10\sqrt{3} $ .故选 $ \mathrm{C} $ .
13．如图，在凸四边形 $ ABCD $ 中， $ AB=1 $ ， $ BC=\sqrt{3} $ ， $ AC\perp CD $ ， $ AC=CD $ ，当 $ \mathrm{\angle }ABC $ 变化时，对角线 $ BD $ 的最大值为（ ）
A．3
B．4
C． $ \sqrt{7+2\sqrt{3}} $
D． $ \sqrt{6}+1 $
设 $ \mathrm{\angle }ABC=\alpha $ , $ \mathrm{\angle }ACB=\beta $ ,则在 $ △ABC $ 中,由余弦定理得 $ A{C}^{2}=4-2\sqrt{3} \cos \alpha $ ,所以 $ C{D}^{2}=4-2\sqrt{3} \cos \alpha $ ,
由正弦定理得 $ \dfrac{AB}{ \sin \beta }=\dfrac{AC}{ \sin \alpha } $ ,
则 $ \sin \beta =\dfrac{AB \sin \alpha }{AC}=\dfrac{ \sin \alpha }{\sqrt{4-2\sqrt{3} \cos \alpha }} $ .
在 $ △BCD $ 中,由余弦定理得 $ B{D}^{2}=B{C}^{2}+C{D}^{2}-2BC\cdot CD \cos (\beta +\dfrac{\mathrm{\pi }}{2})=3+4-2\sqrt{3} \cos \alpha -2\sqrt{3}\sqrt{4-2\sqrt{3} \cos \alpha }\cdot \cos (\beta +\dfrac{\mathrm{\pi }}{2})=7+2\sqrt{3} \sin \alpha -2\sqrt{3} \cos \alpha =7+2\sqrt{6} \sin (\alpha -\dfrac{\mathrm{\pi }}{4}) $ ,
又 $ \alpha \in (0,\mathrm{\pi }) $ ,则 $ \alpha -\dfrac{\mathrm{\pi }}{4}\in (-\dfrac{\mathrm{\pi }}{4},\dfrac{3\mathrm{\pi }}{4}) $ ,所以当 $ \alpha -\dfrac{\mathrm{\pi }}{4}=\dfrac{\mathrm{\pi }}{2} $ ,即 $ \alpha =\dfrac{3\mathrm{\pi }}{4} $ 时, $ B{D}^{2} $ 取得最大值 $ 7+2\sqrt{6} $ ,此时 $ BD=\sqrt{6}+1 $ .故选 $ \mathrm{D} $ .
14．（多选）如图，已知圆 $ O $ 的内接四边形 $ ABCD $ 中， $ AB=2 $ ， $ BC=6 $ ， $ AD=CD=4 $ ，下列说法正确的是（ ）
（多选）
A．四边形 $ ABCD $ 的面积为 $ 8\sqrt{3} $
B．该外接圆的直径为 $ \dfrac{2\sqrt{21}}{3} $
C． $ \overrightarrow {BO}\cdot \overrightarrow {CD}=-4 $
D．过 $ D $ 作 $ DF\perp BC $ 交 $ BC $ 于点 $ F $ ，则 $ \overrightarrow {DO}\cdot \overrightarrow {DF}=10 $
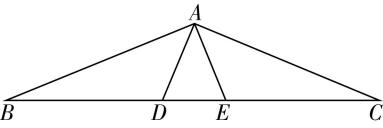
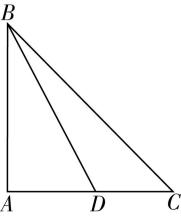
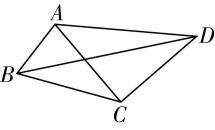
对于 $ \mathrm{A} $ ,如图①,连接 $ AC $ ,在 $ △ACD $ 中, $ \cos D=\dfrac{16+16-A{C}^{2}}{32} $ ,
图①
在 $ △ACB $ 中, $ \cos B=\dfrac{4+36-A{C}^{2}}{24} $ ,
因为 $ B+D=\mathrm{\pi } $ ,所以 $ \cos B+ \cos D=0 $ ,故 $ \dfrac{40-A{C}^{2}}{24}+\dfrac{32-A{C}^{2}}{32}=0 $ ,解得 $ A{C}^{2}=\dfrac{256}{7} $ ,
所以 $ \cos D=-\dfrac{1}{7} $ , $ \cos B=\dfrac{1}{7} $ ,
所以 $ \sin B= \sin D=\sqrt{1-\dfrac{1}{49}}=\dfrac{4\sqrt{3}}{7} $ ,
故 $ {S}_{△ABC}=\dfrac{1}{2}AB\cdot BC \sin B=\dfrac{1}{2}×2×6×\dfrac{4\sqrt{3}}{7}=\dfrac{24\sqrt{3}}{7} $ ,
$ {S}_{△ADC}=\dfrac{1}{2}AD\cdot DC \sin D=\dfrac{1}{2}×4×4×\dfrac{4\sqrt{3}}{7}=\dfrac{32\sqrt{3}}{7} $ ,
故四边形 $ ABCD $ 的面积为 $ \dfrac{24\sqrt{3}}{7}+\dfrac{32\sqrt{3}}{7}=8\sqrt{3} $ ,故 $ \mathrm{A} $ 正确；
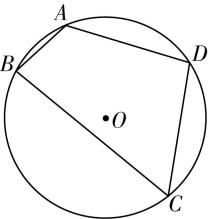
对于 $ \mathrm{B} $ ,设外接圆半径为 $ R $ ,则 $ 2R=\dfrac{AC}{ \sin B}=\dfrac{\sqrt{\dfrac{256}{7}}}{\dfrac{4\sqrt{3}}{7}}=\dfrac{4\sqrt{21}}{3} $ ,
故该外接圆的直径为 $ \dfrac{4\sqrt{21}}{3} $ ,半径为 $ \dfrac{2\sqrt{21}}{3} $ ,故 $ \mathrm{B} $ 错误；
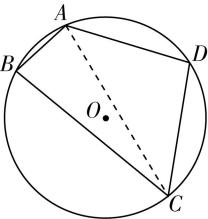
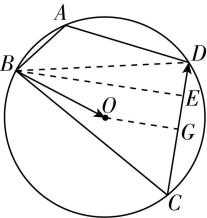
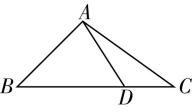
对于 $ \mathrm{C} $ ,如图②,连接 $ BD $ ,过点 $ O $ 作 $ OG\perp CD $ 于点 $ G $ ,过点 $ B $ 作 $ BE\perp CD $ 于点 $ E $ ,则由垂径定理得 $ CG=\dfrac{1}{2}CD=2 $ ,因为 $ A+C=\mathrm{\pi } $ ,所以 $ \cos A+ \cos C=0 $ ,即 $ \dfrac{4+16-B{D}^{2}}{16}+\dfrac{16+36-B{D}^{2}}{48}=0 $ ,解得 $ BD=2\sqrt{7} $ ,所以 $ \cos C=\dfrac{1}{2} $ ,则 $ C=\dfrac{\mathrm{\pi }}{3} $ ,且 $ CE=BC\cdot \cos C=6×\dfrac{1}{2}=3 $ ,所以 $ |\overrightarrow {EG}|=3-2=1 $ ,即 $ \overrightarrow {BO} $ 在向量 $ \overrightarrow {CD} $ 上的投影向量的模为1,且 $ \overrightarrow {EG} $ 与 $ \overrightarrow {CD} $ 反向,故 $ \overrightarrow {BO}\cdot \overrightarrow {CD}=-|\overrightarrow {EG}|\cdot |\overrightarrow {CD}|=-4 $ ,故 $ \mathrm{C} $ 正确；
图②
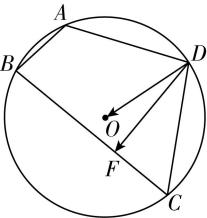
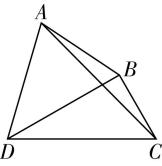
对于 $ \mathrm{D} $ ,如图③，由 $ \mathrm{C} $ 选项可知 $ C=\dfrac{\mathrm{\pi }}{3} $ ,故 $ |\overrightarrow {DF}|=CD\cdot \sin \dfrac{\mathrm{\pi }}{3}=4×\dfrac{\sqrt{3}}{2}=2\sqrt{3} $ ,且 $ \mathrm{\angle }CDF=\dfrac{\mathrm{\pi }}{6} $ ,
图③
因为 $ AD=CD $ ,由对称性可知 $ DO $ 为 $ \mathrm{\angle }ADC $ 的平分线,故 $ \mathrm{\angle }ODF=\dfrac{1}{2}\mathrm{\angle }ADC-\dfrac{\mathrm{\pi }}{6} $ ,
由 $ \mathrm{A} $ 选项可知 $ \cos \mathrm{\angle }ADC=-\dfrac{1}{7} $ ,显然 $ \dfrac{1}{2}\mathrm{\angle }ADC $ 为锐角,
故 $ \cos \dfrac{\mathrm{\angle }ADC}{2}=\sqrt{\dfrac{1+ \cos \mathrm{\angle }ADC}{2}}=\dfrac{\sqrt{21}}{7} $ , $ \sin \dfrac{\mathrm{\angle }ADC}{2}=\sqrt{1-\dfrac{3}{7}}=\dfrac{2\sqrt{7}}{7} $ ,
所以 $ \cos \mathrm{\angle }ODF= \cos (\dfrac{1}{2}\mathrm{\angle }ADC-\dfrac{\mathrm{\pi }}{6}) $
$ = \cos \dfrac{\mathrm{\angle }ADC}{2}\cdot \cos \dfrac{\mathrm{\pi }}{6}+ \sin \dfrac{\mathrm{\angle }ADC}{2}\cdot \sin \dfrac{\mathrm{\pi }}{6}=\dfrac{5\sqrt{7}}{14} $ ,
所以 $ \overrightarrow {DO}\cdot \overrightarrow {DF}=|\overrightarrow {DO}||\overrightarrow {DF}|\cdot \cos \mathrm{\angle }ODF=\dfrac{2\sqrt{21}}{3}×2\sqrt{3}×\dfrac{5\sqrt{7}}{14}=10 $ ,故 $ \mathrm{D} $ 正确.
故选 $ \mathrm{A}\mathrm{C}\mathrm{D} $ .
15．如图，在 $ △ABC $ 中， $ \mathrm{\angle }BAC=\dfrac{3\mathrm{\pi }}{4} $ ， $ AB=AC $ ， $ D $ ， $ E $ 是边 $ BC $ 上的两点，且 $ \mathrm{\angle }BAD=\mathrm{\angle }DAE=\mathrm{\angle }EAC $ ，则 $ \dfrac{DE}{BC}= $ .
$ 3-2\sqrt{2} $
因为 $ \mathrm{\angle }BAC=\dfrac{3\mathrm{\pi }}{4} $ , $ AB=AC $ ,所以 $ \mathrm{\angle }ABC=\mathrm{\angle }ACB=\dfrac{\mathrm{\pi }}{8} $ ,
不妨设 $ AB=m $ ,则 $ B{C}^{2}=A{B}^{2}+A{C}^{2}-2AB\cdot AC \cos \mathrm{\angle }BAC=(2+\sqrt{2}){m}^{2} $ .
因为 $ \mathrm{\angle }BAD=\mathrm{\angle }DAE=\mathrm{\angle }EAC $ ,所以 $ \mathrm{\angle }BAE=\dfrac{2}{3}\mathrm{\angle }BAC=\dfrac{\mathrm{\pi }}{2} $ ,
所以 $ BE=\dfrac{AB}{ \cos \mathrm{\angle }ABC}=\dfrac{m}{ \cos \dfrac{\mathrm{\pi }}{8}} $ ,同理可得 $ CD=\dfrac{m}{ \cos \dfrac{\mathrm{\pi }}{8}} $ .
因为 $ BE+CD=BC+DE $ ,所以 $ DE=2BE-BC $ ,故 $ \dfrac{DE}{BC}=\dfrac{2BE-BC}{BC}=\dfrac{2BE}{BC}-1 $ ,
由二倍角的余弦公式可得 $ \cos \dfrac{\mathrm{\pi }}{4}=2 \cos \hat{}2\dfrac{\mathrm{\pi }}{8}-1 $ ,可得 $ \cos \dfrac{\mathrm{\pi }}{8}=\sqrt{\dfrac{1+ \cos \dfrac{\mathrm{\pi }}{4}}{2}}=\dfrac{\sqrt{2+\sqrt{2}}}{2} $ ,
所以 $ \dfrac{DE}{BC}=\dfrac{2BE}{BC}-1=\dfrac{\dfrac{2m}{\dfrac{\sqrt{2+\sqrt{2}}}{2}}}{\sqrt{2+\sqrt{2}}\cdot m}-1=\dfrac{4}{2+\sqrt{2}}-1=3-2\sqrt{2} $ .