第六章高考强化
一、刷真题
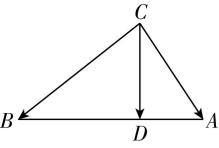
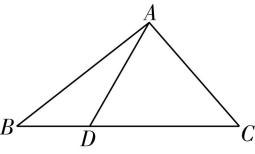
1.在 $ △ABC $ 中,点 $ D $ 在边 $ AB $ 上, $ BD=2DA $ .记 $ \overrightarrow {CA}=\boldsymbol{m} $ , $ \overrightarrow {CD}=\boldsymbol{n} $ ,则 $ \overrightarrow {CB}= $ ( )
A. $ 3\boldsymbol{m}-2\boldsymbol{n} $
B. $ -2\boldsymbol{m}+3\boldsymbol{n} $
C. $ 3\boldsymbol{m}+2\boldsymbol{n} $
D. $ 2\boldsymbol{m}+3\boldsymbol{n} $
答案:B
解析:如图,因为点 $ D $ 在边 $ AB $ 上, $ BD=2DA $ ,所以 $ \overrightarrow {CB}=\overrightarrow {CA}+\overrightarrow {AB}=\overrightarrow {CA}+3\overrightarrow {AD}=\overrightarrow {CA}+3(\overrightarrow {CD}-\overrightarrow {CA})=-2\overrightarrow {CA}+3\overrightarrow {CD}=-2\boldsymbol{m}+3\boldsymbol{n} $ ,故选 $ \mathrm{B} $ .
2.已知向量 $ \boldsymbol{a} $ , $ \boldsymbol{b} $ 满足 $ |\boldsymbol{a}|=1 $ , $ |\boldsymbol{a}+2\boldsymbol{b}|=2 $ ,且 $ (\boldsymbol{b}-2\boldsymbol{a})\perp \boldsymbol{b} $ ,则 $ |\boldsymbol{b}|= $ ( )
A. $ \dfrac{1}{2} $
B. $ \dfrac{\sqrt{2}}{2} $
C. $ \dfrac{\sqrt{3}}{2} $
D. 1
答案:B
解析:因为 $ (\boldsymbol{b}-2\boldsymbol{a})\perp \boldsymbol{b} $ ,所以 $ \boldsymbol{b}\cdot \boldsymbol{b}-2\boldsymbol{a}\cdot \boldsymbol{b}=0 $ ,即 $ {\boldsymbol{b}}^{2}=2\boldsymbol{a}\cdot \boldsymbol{b} $ .又 $ |\boldsymbol{a}+2\boldsymbol{b}|=2 $ ,所以 $ |\boldsymbol{a}+2\boldsymbol{b}{|}^{2}=(\boldsymbol{a}+2\boldsymbol{b})^{2}={\boldsymbol{a}}^{2}+4\boldsymbol{a}\cdot \boldsymbol{b}+4{\boldsymbol{b}}^{2}={\boldsymbol{a}}^{2}+2{\boldsymbol{b}}^{2}+4{\boldsymbol{b}}^{2}=1+6|\boldsymbol{b}{|}^{2}=4 $ ,解得 $ |\boldsymbol{b}{|}^{2}=\dfrac{1}{2} $ , $ |\boldsymbol{b}|=\dfrac{\sqrt{2}}{2} $ ,故选B.
3.已知向量 $ \boldsymbol{a} $ , $ \boldsymbol{b} $ , $ \boldsymbol{c} $ 满足 $ |\boldsymbol{a}|=|\boldsymbol{b}|=1 $ , $ |\boldsymbol{c}|=\sqrt{2} $ ,且 $ \boldsymbol{a}+\boldsymbol{b}+\boldsymbol{c}=0 $ ,则 $ \cos ⟨\boldsymbol{a}-\boldsymbol{c} $ , $ \boldsymbol{b}-\boldsymbol{c}⟩= $ ( )
A. $ -\dfrac{4}{5} $
B. $ -\dfrac{2}{5} $
C. $ \dfrac{2}{5} $
D. $ \dfrac{4}{5} $
答案:D
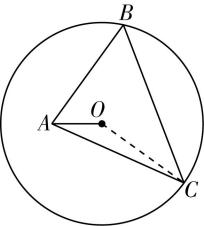
解析:设 $ \overrightarrow {OA}=\boldsymbol{a} $ , $ \overrightarrow {OB}=\boldsymbol{b} $ , $ \overrightarrow {OC}=\boldsymbol{c} $ ,因为 $ |\boldsymbol{a}|=|\boldsymbol{b}|=1 $ , $ |\boldsymbol{c}|=\sqrt{2} $ ,且 $ \boldsymbol{a}+\boldsymbol{b}+\boldsymbol{c}=0 $ ,所以 $ \boldsymbol{a}\perp \boldsymbol{b} $ ,如图.
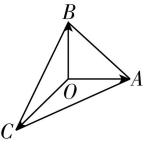
因为 $ \boldsymbol{a}-\boldsymbol{c}=\overrightarrow {OA}-\overrightarrow {OC}=\overrightarrow {CA} $ , $ \boldsymbol{b}-\boldsymbol{c}=\overrightarrow {OB}-\overrightarrow {OC}=\overrightarrow {CB} $ ,所以 $ ⟨\boldsymbol{a}-\boldsymbol{c} $ , $ \boldsymbol{b}-\boldsymbol{c}⟩=\mathrm{\angle }ACB $ .
由题意可知, $ \mathrm{\angle }AOC=\mathrm{\angle }BOC=\dfrac{3\mathrm{\pi }}{4} $ ,在 $ △AOC $ 中,由余弦定理得, $ A{C}^{2}=O{A}^{2}+O{C}^{2}-2OA\cdot OC\cdot \cos \mathrm{\angle }AOC={1}^{2}+ (\sqrt{2})^{2}-2×1×\sqrt{2}× (-\dfrac{\sqrt{2}}{2} )=5 $ ,所以 $ AC=BC=\sqrt{5} $ .在 $ △ABC $ 中, $ AB=\sqrt{2} $ ,由余弦定理得, $ \cos \mathrm{\angle }ACB=\dfrac{A{C}^{2}+B{C}^{2}-A{B}^{2}}{2AC\cdot BC}=\dfrac{(\sqrt{5})^{2}+(\sqrt{5})^{2}-(\sqrt{2})^{2}}{2\sqrt{5}×\sqrt{5}}=\dfrac{4}{5} $ ,所以 $ \cos ⟨\boldsymbol{a}-\boldsymbol{c} $ , $ \boldsymbol{b}-\boldsymbol{c}⟩=\dfrac{4}{5} $ ,故选 $ \mathrm{D} $ .
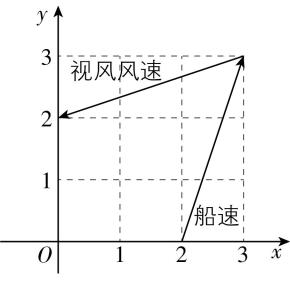
4.帆船比赛中,运动员可借助风力计测定风速的大小与方向,测出的结果在航海学中称为视风风速.视风风速对应的向量是真风风速对应的向量与船行风风速对应的向量之和,其中船行风风速对应的向量与船速对应的向量大小相等、方向相反.表中给出了部分风力等级、名称与风速大小的对应关系.已知某帆船运动员在某时刻测得的视风风速对应的向量与船速对应的向量如图所示(线段长度代表速度大小,单位: $ \mathrm{m}/\mathrm{s} $ ),则该时刻的真风为( )
级数 | 名称 | 风速大小(单位: $ \mathrm{m}/\mathrm{s} $ ) |
2 | 轻风 | $ 1.6~3.3 $ |
3 | 微风 | $ 3.4~5.4 $ |
4 | 和风 | $ 5.5~7.9 $ |
5 | 劲风 | $ 8.0~10.7 $ |
A.轻风
B.微风
C.和风
D.劲风
答案:A
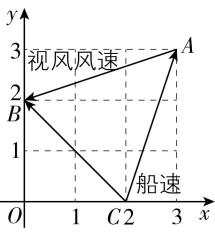
解析:如图,设点 $ A(3,3) $ , $ B(0,2) $ , $ C(2,0) $ ,由题意知,视风风速对应的向量为 $ \overrightarrow {AB} $ ,船速对应的向量为 $ \overrightarrow {CA} $ ,因为船行风风速对应的向量与船速对应的向量为相反向量,所以船行风风速对应的向量为 $ \overrightarrow {AC} $ ,则真风风速对应的向量为 $ \overrightarrow {AB}-\overrightarrow {AC}=\overrightarrow {CB}=(-2,2) $ , $ |\overrightarrow {CB}|=\sqrt{(-2)^{2}+{2}^{2}}=2\sqrt{2} $ ,而 $ 2\sqrt{2}\in (1.6,3.3) $ ,故该时刻的真风为轻风.故选 $ \mathrm{A} $ .
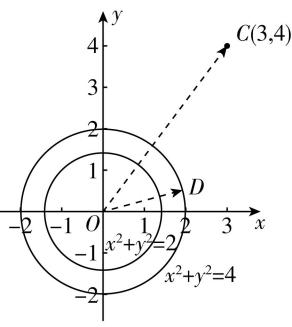
5.在平面直角坐标系 $ xOy $ 中, $ |\overrightarrow {OA}|=|\overrightarrow {OB}|=\sqrt{2} $ , $ |\overrightarrow {AB}|=2 $ ,设 $ C(3,4) $ ,则 $ |2\overrightarrow {CA}+\overrightarrow {AB}| $ 的取值范围是( )
A. $ [6,14] $
B. $ [6,12] $
C. $ [8,14] $
D. $ [8,12] $
答案:D
解析: $ \because |\overrightarrow {OA}|=|\overrightarrow {OB}|=\sqrt{2} $ , $ |\overrightarrow {AB}|=2 $ , $ \therefore |\overrightarrow {OA}{|}^{2}+|\overrightarrow {OB}{|}^{2}=|\overrightarrow {AB}{|}^{2}=4 $ , $ \therefore OA\perp OB $ 且点 $ A $ , $ B $ 在以点 $ O $ 为圆心, $ \sqrt{2} $ 为半径的圆上, $ \therefore |2\overrightarrow {CA}+\overrightarrow {AB}|=|\overrightarrow {CA}+\overrightarrow {CB}|=|\overrightarrow {OA}-\overrightarrow {OC}+\overrightarrow {OB}-\overrightarrow {OC}|=|\overrightarrow {OA}+\overrightarrow {OB}-2\overrightarrow {OC}| $ , $ \therefore |2\overrightarrow {CA}+\overrightarrow {AB}{|}^{2}= (\overrightarrow {OA}+\overrightarrow {OB})^{2}+4{\overrightarrow {OC}}^{2}-4 (\overrightarrow {OA}+\overrightarrow {OB} )\cdot \overrightarrow {OC}={\overrightarrow {OA}}^{2}+{\overrightarrow {OB}}^{2}+4{\overrightarrow {OC}}^{2}-4 (\overrightarrow {OA}+\overrightarrow {OB} )\cdot \overrightarrow {OC}=104-4 (\overrightarrow {OA}+\overrightarrow {OB} )\cdot \overrightarrow {OC} $ .
令 $ \overrightarrow {OD}=\overrightarrow {OA}+\overrightarrow {OB} $ ,则点 $ D $ 在以点 $ O $ 为圆心,2为半径的圆上,
$ \therefore (\overrightarrow {OA}+\overrightarrow {OB})\cdot \overrightarrow {OC}=\overrightarrow {OD}\cdot \overrightarrow {OC}=|\overrightarrow {OD}||\overrightarrow {OC}|\cdot \cos ⟨\overrightarrow {OD} $ , $ \overrightarrow {OC}⟩=10 \cos ⟨\overrightarrow {OD} $ , $ \overrightarrow {OC}⟩ $ .
$ \because ⟨\overrightarrow {OD} $ , $ \overrightarrow {OC}⟩\in [0,\mathrm{\pi }] $ , $ \therefore (\overrightarrow {OA}+\overrightarrow {OB})\cdot \overrightarrow {OC}\in [-10,10] $ ,
$ \therefore |2\overrightarrow {CA}+\overrightarrow {AB}{|}^{2}=104-4(\overrightarrow {OA}+\overrightarrow {OB})\cdot \overrightarrow {OC}\in [64,144] $ ,
$ \therefore |2\overrightarrow {CA}+\overrightarrow {AB}|\in [8,12] $ .故选 $ \mathrm{D} $ .
6.已知 $ \odot O $ 的半径为1,直线 $ PA $ 与 $ \odot O $ 相切于点 $ A $ ,直线 $ PB $ 与 $ \odot O $ 交于 $ B $ , $ C $ 两点, $ D $ 为 $ BC $ 的中点.若 $ |PO|=\sqrt{2} $ ,则 $ \overrightarrow {PA}\cdot \overrightarrow {PD} $ 的最大值为( )
A. $ \dfrac{1}{2}+\dfrac{\sqrt{2}}{2} $
B. $ \dfrac{1}{2}+\sqrt{2} $
C. $ 1+\sqrt{2} $
D. $ 2+\sqrt{2} $
答案:A
解析:直线 $ PA $ 与 $ \odot O $ 相切于 $ A $ ,且 $ |OA|=1 $ , $ |PO|=\sqrt{2} $ ,则 $ |PA|=1 $ .设 $ \overrightarrow {PO} $ 与 $ \overrightarrow {PD} $ 的夹角为 $ \theta $ ,则 $ \theta \in [0,\dfrac{\mathrm{\pi }}{4}) $ .
当 $ PA $ 与 $ PD $ 在 $ PO $ 的同侧时, $ \overrightarrow {PA}\cdot \overrightarrow {PD}=|\overrightarrow {PA}||\overrightarrow {PD}|\cdot \cos (\dfrac{\mathrm{\pi }}{4}-\theta )=1×|PO| \cos \theta × \cos (\dfrac{\mathrm{\pi }}{4}-\theta )=\sqrt{2} \cos \theta \cdot \cos (\dfrac{\mathrm{\pi }}{4}-\theta )=\sqrt{2} \cos \theta ×\dfrac{\sqrt{2}}{2}( \cos \theta + \sin \theta )={ \cos }^{2}\theta +\dfrac{1}{2} \sin 2\theta =\dfrac{1}{2}+\dfrac{\sqrt{2}}{2} \sin (2\theta +\dfrac{\mathrm{\pi }}{4})\leqslant \dfrac{1}{2}+\dfrac{\sqrt{2}}{2} $ ;
当 $ PA $ 与 $ PD $ 在 $ PO $ 的异侧时, $ \overrightarrow {PA}\cdot \overrightarrow {PD}=|\overrightarrow {PA}||\overrightarrow {PD}|\cdot \cos (\dfrac{\mathrm{\pi }}{4}+\theta )=1×|PO| \cos \theta × \cos (\dfrac{\mathrm{\pi }}{4}+\theta )=\sqrt{2} \cos \theta \cdot \cos (\dfrac{\mathrm{\pi }}{4}+\theta )=\sqrt{2} \cos \theta ×\dfrac{\sqrt{2}}{2}( \cos \theta - \sin \theta )={ \cos }^{2}\theta -\dfrac{1}{2} \sin 2\theta =\dfrac{1}{2}+\dfrac{\sqrt{2}}{2} \cos (2\theta +\dfrac{\mathrm{\pi }}{4})\leqslant \dfrac{1}{2}+\dfrac{1}{2}=1 $ .综上所述, $ \overrightarrow {PA}\cdot \overrightarrow {PD} $ 的最大值为 $ \dfrac{1}{2}+\dfrac{\sqrt{2}}{2} $ ,故选 $ \mathrm{A} $ .
7.(多选)已知 $ O $ 为坐标原点,点 $ {P}_{1}( \cos \alpha , \sin \alpha ) $ , $ {P}_{2}( \cos \beta ,- \sin \beta ) $ , $ {P}_{3}( \cos (\alpha +\beta ), \sin (\alpha +\beta )) $ , $ A(1,0) $ ,则( )(多选)
A. $ |\overrightarrow {O{P}_{1}}|=|\overrightarrow {O{P}_{2}}| $
B. $ |\overrightarrow {A{P}_{1}}|=|\overrightarrow {A{P}_{2}}| $
C. $ \overrightarrow {OA}\cdot \overrightarrow {O{P}_{3}}=\overrightarrow {O{P}_{1}}\cdot \overrightarrow {O{P}_{2}} $
D. $ \overrightarrow {OA}\cdot \overrightarrow {O{P}_{1}}=\overrightarrow {O{P}_{2}}\cdot \overrightarrow {O{P}_{3}} $
答案:AC
解析:对于选项 $ \mathrm{A} $ ,因为 $ \overrightarrow {O{P}_{1}}=( \cos \alpha , \sin \alpha ) $ , $ \overrightarrow {O{P}_{2}}=( \cos \beta ,- \sin \beta ) $ ,所以 $ |\overrightarrow {O{P}_{1}}|=\sqrt{{ \cos }^{2}\alpha +{ \sin }^{2}\alpha }=1 $ , $ |\overrightarrow {O{P}_{2}}|=\sqrt{{ \cos }^{2}\beta +(- \sin \beta )^{2}}=1 $ ,则 $ |\overrightarrow {O{P}_{1}}|=|\overrightarrow {O{P}_{2}}| $ ,故 $ \mathrm{A} $ 正确;对于选项 $ \mathrm{B} $ ,因为 $ \overrightarrow {A{P}_{1}}=( \cos \alpha -1, \sin \alpha ) $ , $ \overrightarrow {A{P}_{2}}=( \cos \beta -1,- \sin \beta ) $ ,所以 $ |\overrightarrow {A{P}_{1}}|=\sqrt{{\left( \cos \alpha -1\right) ^ {2}}+{ \sin }^{2}\alpha }=\sqrt{2-2 \cos }\alpha $ , $ |\overrightarrow {A{P}_{2}}|=\sqrt{( \cos \beta -1)^{2}+(- \sin \beta )^{2}}=\sqrt{2-2\mathrm{ \cos }\beta } $ ,当 $ \cos \alpha \ne \cos \beta $ 时, $ |\overrightarrow {A{P}_{1}}|\ne |\overrightarrow {A{P}_{2}}| $ ,故 $ \mathrm{B} $ 错误;对于选项 $ \mathrm{C} $ , $ \overrightarrow {OA}=(1,0) $ , $ \overrightarrow {O{P}_{3}}=( \cos (\alpha +\beta ), \sin (\alpha +\beta )) $ ,所以 $ \overrightarrow {OA}\cdot \overrightarrow {O{P}_{3}}= \cos (\alpha +\beta ) $ , $ \overrightarrow {O{P}_{1}}\cdot \overrightarrow {O{P}_{2}}= \cos \alpha \cos \beta - \sin \alpha \sin \beta = \cos (\alpha +\beta ) $ ,所以 $ \overrightarrow {OA}\cdot \overrightarrow {O{P}_{3}}=\overrightarrow {O{P}_{1}}\cdot \overrightarrow {O{P}_{2}} $ ,故 $ \mathrm{C} $ 正确;对于选项 $ \mathrm{D} $ , $ \overrightarrow {OA}\cdot \overrightarrow {O{P}_{1}}= \cos \alpha $ , $ \overrightarrow {O{P}_{2}}\cdot \overrightarrow {O{P}_{3}}= \cos \beta \cos (\alpha +\beta )- \sin \beta \sin (\alpha +\beta )= \cos [\beta +(\alpha +\beta )]= \cos (\alpha +2\beta ) $ ,当 $ \beta \ne k\mathrm{\pi } $ 且 $ \beta \ne k\mathrm{\pi }-\alpha (k\in \boldsymbol{Z}) $ 时, $ \overrightarrow {OA}\cdot \overrightarrow {O{P}_{1}}\ne \overrightarrow {O{P}_{2}}\cdot \overrightarrow {O{P}_{3}} $ ,故 $ \mathrm{D} $ 错误.故选 $ \mathrm{A}\mathrm{C} $ .
8.在 $ △ABC $ 中, $ D $ 为 $ AB $ 中点, $ \overrightarrow {CE}=\dfrac{1}{3}\overrightarrow {CD} $ ,记 $ \overrightarrow {AB}=\boldsymbol{a} $ , $ \overrightarrow {AC}=\boldsymbol{b} $ ,则 $ \overrightarrow {AE}= $ (用 $ \boldsymbol{a} $ , $ \boldsymbol{b} $ 表示);若 $ |\overrightarrow {AE}|=5 $ , $ AE\perp CB $ ,则 $ \overrightarrow {AE}\cdot \overrightarrow {CD}= $ .
答案: $ \dfrac{1}{6}\boldsymbol{a}+\dfrac{2}{3}\boldsymbol{b} $ ; $ -15 $
解析:依题意, $ \overrightarrow {AE}=\overrightarrow {AC}+\overrightarrow {CE}=\boldsymbol{b}+\dfrac{1}{3}\overrightarrow {CD} $ ,因为 $ D $ 是 $ AB $ 中点,所以 $ \overrightarrow {CD}=\dfrac{1}{2}\overrightarrow {CA}+\dfrac{1}{2}\overrightarrow {CB}=\dfrac{1}{2}\overrightarrow {CA}+\dfrac{1}{2}(\overrightarrow {AB}-\overrightarrow {AC})=\dfrac{1}{2}\overrightarrow {AB}-\overrightarrow {AC}=\dfrac{1}{2}\boldsymbol{a}-\boldsymbol{b} $ ,所以 $ \overrightarrow {AE}=\boldsymbol{b}+\dfrac{1}{3}(\dfrac{1}{2}\boldsymbol{a}-\boldsymbol{b})=\dfrac{1}{6}\boldsymbol{a}+\dfrac{2}{3}\boldsymbol{b} $ .
因为 $ |\overrightarrow {AE}|=5 $ , $ AE\perp CB $ ,所以 $ \begin{cases}{\left(\dfrac{1}{6}\boldsymbol{a}+\dfrac{2}{3}\boldsymbol{b}\right) ^ {2}}=25,\\ (\dfrac{1}{6}\boldsymbol{a}+\dfrac{2}{3}\boldsymbol{b})\cdot (\boldsymbol{a}-\boldsymbol{b})=0,\end{cases} $
即 $ \begin{cases}\dfrac{1}{36}{\mid \boldsymbol{a}\mid }^{2}+\dfrac{2}{9}\boldsymbol{a}\cdot \boldsymbol{b}+\dfrac{4}{9}{\mid \boldsymbol{b}\mid }^{2}=25,\\ \dfrac{1}{6}{\mid \boldsymbol{a}\mid }^{2}+\dfrac{1}{2}\boldsymbol{a}\cdot \boldsymbol{b}-\dfrac{2}{3}{\mid \boldsymbol{b}\mid }^{2}=0,\end{cases} $
即 $ \begin{cases}{\mid \boldsymbol{a}\mid }^{2}+8\boldsymbol{a}\cdot \boldsymbol{b}+16{\mid \boldsymbol{b}\mid }^{2}=900,①\\ {\mid \boldsymbol{a}\mid }^{2}-4{\mid \boldsymbol{b}\mid }^{2}+3\boldsymbol{a}\cdot \boldsymbol{b}=0,②\end{cases} $
由②得 $ {|\boldsymbol{a}|}^{2}=4{|\boldsymbol{b}|}^{2}-3\boldsymbol{a}\cdot \boldsymbol{b} $ ,代入①得 $ 20|\boldsymbol{b}{|}^{2}+5\boldsymbol{a}\cdot \boldsymbol{b}=900 $ ,
则 $ \overrightarrow {AE}\cdot \overrightarrow {CD}=(\dfrac{1}{6}\boldsymbol{a}+\dfrac{2}{3}\boldsymbol{b})\cdot (\dfrac{1}{2}\boldsymbol{a}-\boldsymbol{b})=\dfrac{1}{12}{|\boldsymbol{a}|}^{2}+\dfrac{1}{6}\boldsymbol{a}\cdot \boldsymbol{b}-\dfrac{2}{3}{|\boldsymbol{b}|}^{2}=-\dfrac{1}{3}{|\boldsymbol{b}|}^{2}-\dfrac{1}{12}\boldsymbol{a}\cdot \boldsymbol{b}=-\dfrac{1}{60}(20{|\boldsymbol{b}|}^{2}+5\boldsymbol{a}\cdot \boldsymbol{b})=-\dfrac{900}{60}=-15 $ .
【多种解法一】
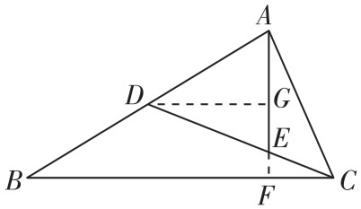
如图,延长 $ AE $ 交 $ BC $ 于 $ F $ ,则 $ AF\perp BC $ ,过 $ D $ 作 $ DG\perp AF $ 于 $ G $ ,所以 $ △CEF\sim △DEG $ ,
设 $ EF=x $ ,则 $ \dfrac{EG}{EF}=\dfrac{DE}{EC}=\dfrac{2}{1} $ ,所以 $ EG=2x $ .
又 $ D $ 为 $ AB $ 中点, $ DG//BF $ ,所以 $ AG=FG=3x $ ,所以 $ AE=AG+GE=3x+2x=5 $ ,
解得 $ x=1 $ ,即 $ EF=1 $ ,
所以 $ \overrightarrow {AE}\cdot \overrightarrow {CD}=\overrightarrow {AE}\cdot 3\overrightarrow {CE}=3|\overrightarrow {AE}||\overrightarrow {CE}|\cdot \cos ⟨\overrightarrow {AE} $ , $ \overrightarrow {CE}⟩=3|\overrightarrow {AE}||\overrightarrow {CE}|(- \cos \mathrm{\angle }CEF)=3|\overrightarrow {AE}||\overrightarrow {CE}|(-\dfrac{|\overrightarrow {EF}|}{|\overrightarrow {CE}|})=-3|\overrightarrow {AE}|\cdot |\overrightarrow {EF}|=-15 $ .
【多种解法二】
延长 $ AE $ 交 $ BC $ 于 $ F $ ,则 $ AF\perp BC. $
$ \overrightarrow {AE}\cdot \overrightarrow {CD}=\overrightarrow {AE}\cdot (\overrightarrow {CB}+\overrightarrow {BD})=\overrightarrow {AE}\cdot \overrightarrow {CB}+\overrightarrow {AE}\cdot \overrightarrow {BD}=0+\overrightarrow {AE}\cdot (-\dfrac{1}{2}\overrightarrow {AB})=-\dfrac{1}{2}\overrightarrow {AE}\cdot \overrightarrow {AB} $ .
设 $ \overrightarrow {AE} $ 与 $ \overrightarrow {AB} $ 的夹角为 $ \theta $ ,则 $ \overrightarrow {AE}\cdot \overrightarrow {CD}=-\dfrac{1}{2}\cdot |\overrightarrow {AE}|\cdot |\overrightarrow {AB}| \cos \theta $ $ =-\dfrac{1}{2}×5|\overrightarrow {AF}| $ .
设 $ \overrightarrow {AF}=\lambda \overrightarrow {AE}=\lambda (\dfrac{2}{3}\overrightarrow {AC}+\dfrac{1}{6}\overrightarrow {AB})=\dfrac{2}{3}\lambda \overrightarrow {AC}+\dfrac{\lambda }{6}\overrightarrow {AB} $ ,
因为 $ B $ , $ F $ , $ C $ 三点共线,所以 $ \dfrac{2}{3}\lambda +\dfrac{\lambda }{6}=1 $ ,解得 $ \lambda =\dfrac{6}{5} $ ,
所以 $ \overrightarrow {AF}=\dfrac{6}{5}\overrightarrow {AE} $ ,即 $ |\overrightarrow {AF}|=6 $ ,
所以 $ \overrightarrow {AE}\cdot \overrightarrow {CD}=-\dfrac{1}{2}×5×6=-15 $ .
9.设向量 $ \boldsymbol{a}=(x+1,x) $ , $ \boldsymbol{b}=(x,2) $ ,则( )
A. $ x=-3 $ 是 $ \boldsymbol{a}\perp \boldsymbol{b} $ 的必要条件
B. $ x=1+\sqrt{3} $ 是 $ \boldsymbol{a}//\boldsymbol{b} $ 的必要条件
C. $ x=0 $ 是 $ \boldsymbol{a}\perp \boldsymbol{b} $ 的充分条件
D. $ x=-1+\sqrt{3} $ 是 $ \boldsymbol{a}//\boldsymbol{b} $ 的充分条件
答案:C
解析:因为 $ \boldsymbol{a}=(x+1,x) $ , $ \boldsymbol{b}=(x,2) $ ,所以 $ \boldsymbol{a}\perp \boldsymbol{b} $ 的充要条件为 $ \boldsymbol{a}\cdot \boldsymbol{b}=0 $ ,即 $ (x+1)\cdot x+2x=0 $ ,解得 $ x=0 $ 或 $ x=-3 $ ,故 $ \mathrm{A} $ 错误, $ \mathrm{C} $ 正确 $ .\boldsymbol{a}//\boldsymbol{b} $ 的充要条件为 $ 2(x+1)={x}^{2} $ ,即 $ {x}^{2}-2x-2=0 $ ,解得 $ x=1±\sqrt{3} $ ,故 $ \mathrm{B} $ , $ \mathrm{D} $ 错误.故选 $ \mathrm{C} $ .
10.已知平面向量 $ \boldsymbol{a}=(x,1) $ , $ \boldsymbol{b}=(x-1,2x) $ .若 $ \boldsymbol{a}\perp (\boldsymbol{a}-\boldsymbol{b}) $ ,则 $ |\boldsymbol{a}|= $ .
解析:由题意得 $ \boldsymbol{a}-\boldsymbol{b}=(1,1-2x) $ ,由 $ \boldsymbol{a}\perp (\boldsymbol{a}-\boldsymbol{b}) $ ,得 $ \boldsymbol{a}\cdot (\boldsymbol{a}-\boldsymbol{b})=0 $ ,即 $ x+1-2x=0 $ ,所以 $ x=1 $ ,所以 $ \boldsymbol{a}=(1,1) $ ,故 $ |\boldsymbol{a}|=\sqrt{2} $ .
11.在 $ △ABC $ 中, $ BC=2 $ , $ AC=1+\sqrt{3} $ , $ AB=\sqrt{6} $ ,则 $ A= $ ( )
A. $ {45}^{\circ } $
B. $ {60}^{\circ } $
C. $ {120}^{\circ } $
D. $ {135}^{\circ } $
答案:A
解析:根据余弦定理有 $ \cos A=\dfrac{A{B}^{2}+A{C}^{2}-B{C}^{2}}{2\cdot AB\cdot AC}=\dfrac{6+4+2\sqrt{3}-4}{2\sqrt{6}(1+\sqrt{3})}=\dfrac{\sqrt{2}}{2} $ ,因为 $ {0}^{\circ } < A < {180}^{\circ } $ ,所以 $ A={45}^{\circ } $ .故选 $ \mathrm{A} $ .
12.(多选)已知 $ △ABC $ 的面积为 $ \dfrac{1}{4} $ , $ \cos 2A+ \cos 2B+2 \sin C=2 $ , $ \cos A \cos B \sin C=\dfrac{1}{4} $ ,则( )(多选)
A. $ \sin C={ \sin }^{2}A+{ \sin }^{2}B $
B. $ AB=\sqrt{2} $
C. $ \sin A+ \sin B=\dfrac{\sqrt{6}}{2} $
D. $ A{C}^{2}+B{C}^{2}=3 $
答案:ABC
解析:因为 $ \cos 2A+ \cos 2B+2 \sin C=2 $ ,所以 $ 2{ \cos }^{2}A-1+2{ \cos }^{2}B-1+2 \sin C=2 $ ,即 $ { \cos }^{2}A+{ \cos }^{2}B+ \sin C=2 $ ,
所以 $ 1-{ \sin }^{2}A+1-{ \sin }^{2}B+ \sin C=2 $ ,即 $ \sin C={ \sin }^{2}A+{ \sin }^{2}B $ ,故 $ \mathrm{A} $ 正确.
当 $ C > \dfrac{\mathrm{\pi }}{2} $ 时, $ A+B < \dfrac{\mathrm{\pi }}{2} $ ,即 $ 0 < A < \dfrac{\mathrm{\pi }}{2}-B < \dfrac{\mathrm{\pi }}{2} $ ,故有 $ 0 < \sin A < \sin (\dfrac{\mathrm{\pi }}{2}-B) $ ,即 $ 0 < \sin A < \cos B $ ,同理有 $ 0 < \sin B < \cos A $ ,
所以 $ { \sin }^{2}A+{ \sin }^{2}B < \sin A \cos B+ \sin B \cos A= \sin (A+B)= \sin C $ ,与 $ \mathrm{A} $ 选项矛盾,故 $ C > \dfrac{\mathrm{\pi }}{2} $ 不成立,同理可得 $ C < \dfrac{\mathrm{\pi }}{2} $ 也不成立,故 $ C=\dfrac{\mathrm{\pi }}{2} $ ,则 $ \sin C=1 $ , $ \cos C=0 $ .因为 $ \cos A \cos B\cdot \sin C=\dfrac{1}{4} $ ,所以 $ \cos A \cos B=\dfrac{1}{4} $ ,因为 $ A+B=\dfrac{\mathrm{\pi }}{2} $ ,所以 $ \cos B= \sin A $ ,所以 $ \cos A\cdot \sin A=\dfrac{1}{4} $ ,即 $ \sin 2A=\dfrac{1}{2} $ ,又 $ A\in (0,\dfrac{\mathrm{\pi }}{2}) $ , $ 2A\in (0,\mathrm{\pi }) $ ,故 $ 2A=\dfrac{\mathrm{\pi }}{6} $ 或 $ \dfrac{5\mathrm{\pi }}{6} $ ,即 $ A=\dfrac{\mathrm{\pi }}{12} $ 或 $ \dfrac{5\mathrm{\pi }}{12} $ .当 $ A=\dfrac{\mathrm{\pi }}{12} $ 时, $ \tan \dfrac{\mathrm{\pi }}{12}= \tan (\dfrac{\mathrm{\pi }}{3}-\dfrac{\mathrm{\pi }}{4})=2-\sqrt{3} $ ,所以 $ \dfrac{BC}{AC}=2-\sqrt{3}① $ .
$ {S}_{△ABC}=\dfrac{1}{2}AC\cdot BC=\dfrac{1}{4} $ ,故 $ AC\cdot BC=\dfrac{1}{2}② $ ,
结合①②可得
$ \begin{cases}A{C}^{2}=\dfrac{2+\sqrt{3}}{2},\\ B{C}^{2}=\dfrac{2-\sqrt{3}}{2},\end{cases} $ 所以 $ A{B}^{2}=A{C}^{2}+B{C}^{2}=2 $ ,则 $ AB=\sqrt{2} $ ,故 $ \mathrm{B} $ 正确, $ \mathrm{D} $ 错误.
当 $ A=\dfrac{\mathrm{\pi }}{12} $ 时, $ \sin \dfrac{\mathrm{\pi }}{12}= \sin (\dfrac{\mathrm{\pi }}{3}-\dfrac{\mathrm{\pi }}{4})=\dfrac{\sqrt{6}-\sqrt{2}}{4} $ , $ \sin \dfrac{5\mathrm{\pi }}{12}= \sin (\dfrac{\mathrm{\pi }}{6}+\dfrac{\mathrm{\pi }}{4})=\dfrac{\sqrt{6}+\sqrt{2}}{4} $ ,
所以 $ \sin A+ \sin B=\dfrac{\sqrt{6}-\sqrt{2}}{4}+\dfrac{\sqrt{6}+\sqrt{2}}{4}=\dfrac{\sqrt{6}}{2} $ ,故 $ \mathrm{C} $ 正确.
当 $ A=\dfrac{5\mathrm{\pi }}{12} $ 时,同理可得 $ \mathrm{B} $ 正确, $ \mathrm{C} $ 正确, $ \mathrm{D} $ 错误.故选 $ \mathrm{A}\mathrm{B}\mathrm{C} $ .
13.记 $ △ABC $ 的内角 $ A $ , $ B $ , $ C $ 的对边分别为 $ a $ , $ b $ , $ c $ ,已知 $ B={60}^{\circ } $ , $ {b}^{2}=\dfrac{9}{4}ac $ ,则 $ \sin A+ \sin C= $ ( )
A. $ \dfrac{3}{2} $
B. $ \sqrt{2} $
C. $ \dfrac{\sqrt{7}}{2} $
D. $ \dfrac{\sqrt{3}}{2} $
答案:C
解析: $ \because {b}^{2}=\dfrac{9}{4}ac $ , $ \therefore $ 由正弦定理可得 $ { \sin }^{2}B=\dfrac{9}{4} \sin A \sin C $ .
$ \because B={60}^{\circ } $ , $ \therefore \sin B=\dfrac{\sqrt{3}}{2} $ ,
$ \therefore \dfrac{3}{4}=\dfrac{9}{4} \sin A \sin C $ , $ \therefore \sin A \sin C=\dfrac{1}{3} $ .由余弦定理可得 $ {b}^{2}={a}^{2}+{c}^{2}-2ac \cos B={a}^{2}+{c}^{2}-ac $ ,将 $ {b}^{2}=\dfrac{9}{4}ac $ 代入整理得, $ {a}^{2}+{c}^{2}=\dfrac{13}{4}ac $ , $ \therefore $ 由正弦定理得 $ { \sin }^{2}A+{ \sin }^{2}C=\dfrac{13}{4} \sin A \sin C $ ,则 $ ( \sin A+ \sin C)^{2}={ \sin }^{2}A+{ \sin }^{2}C+2 \sin A \sin C=\dfrac{13}{4} \sin A \sin C+2 \sin A \sin C=\dfrac{21}{4} \sin A \sin C=\dfrac{21}{4}×\dfrac{1}{3}=\dfrac{7}{4} $ , $ \therefore \sin A+ \sin C=\dfrac{\sqrt{7}}{2} $ 或 $ -\dfrac{\sqrt{7}}{2} $ (舍).故选 $ \mathrm{C} $ .
14.在 $ △ABC $ 中, $ \mathrm{\angle }BAC={60}^{\circ } $ , $ AB=2 $ , $ BC=\sqrt{6} $ , $ \mathrm{\angle }BAC $ 的角平分线交 $ BC $ 于 $ D $ ,则 $ AD= $ .
解析:在 $ △ABC $ 中,由余弦定理得 $ \cos \mathrm{\angle }BAC=\dfrac{A{B}^{2}+A{C}^{2}-B{C}^{2}}{2AB\cdot AC}=\dfrac{4+A{C}^{2}-6}{4AC}=\dfrac{1}{2} $ ,所以 $ AC=1+\sqrt{3} $ (舍负).在 $ △ABD $ 中,由正弦定理得 $ \dfrac{BD}{ \sin \mathrm{\angle }BAD}=\dfrac{AB}{ \sin \mathrm{\angle }ADB} $ ,所以 $ \dfrac{ \sin \mathrm{\angle }ADB}{ \sin \mathrm{\angle }BAD}=\dfrac{AB}{BD} $ .在 $ △ACD $ 中,由正弦定理得 $ \dfrac{CD}{ \sin \mathrm{\angle }CAD}=\dfrac{AC}{ \sin \mathrm{\angle }ADC} $ ,所以 $ \dfrac{ \sin \mathrm{\angle }ADC}{ \sin \mathrm{\angle }CAD}=\dfrac{AC}{CD} $ ,又 $ AD $ 平分 $ \mathrm{\angle }BAC $ ,所以 $ \mathrm{\angle }BAD=\mathrm{\angle }CAD $ ,则 $ \sin \mathrm{\angle }BAD= \sin \mathrm{\angle }CAD $ ,又 $ \sin \mathrm{\angle }ADB= \sin \mathrm{\angle }ADC $ ,所以 $ \dfrac{AB}{BD}=\dfrac{AC}{CD} $ ,所以 $ \dfrac{BD}{CD}=\dfrac{AB}{AC}=\dfrac{2}{1+\sqrt{3}} $ ,且 $ BD+CD=\sqrt{6} $ ,所以 $ BD=\dfrac{2\sqrt{6}}{3+\sqrt{3}}=\sqrt{6}-\sqrt{2} $ .在 $ △ABC $ 中,由余弦定理得 $ \cos \mathrm{\angle }ABC=\dfrac{A{B}^{2}+B{C}^{2}-A{C}^{2}}{2AB\cdot BC}=\dfrac{4+6-{\left(1+\sqrt{3}\right) ^ {2}}}{4\sqrt{6}}=\dfrac{\sqrt{6}-\sqrt{2}}{4} $ ,在 $ △ABD $ 中,由余弦定理得 $ \cos \mathrm{\angle }ABD=\dfrac{A{B}^{2}+B{D}^{2}-A{D}^{2}}{2AB\cdot BD}=\dfrac{{2}^{2}+{\left(\sqrt{6}-\sqrt{2}\right) ^ {2}}-A{D}^{2}}{4(\sqrt{6}-\sqrt{2})}=\dfrac{\sqrt{6}-\sqrt{2}}{4} $ ,解得 $ AD=2 $ (舍负).
15.已知 $ △ABC $ 中,点 $ D $ 在边 $ BC $ 上, $ \mathrm{\angle }ADB={120}^{\circ } $ , $ AD=2 $ , $ CD=2BD $ .当 $ \dfrac{AC}{AB} $ 取得最小值时, $ BD= $ .
解析:设 $ CD=2BD=2m > 0 $ ,
则在 $ △ABD $ 中, $ A{B}^{2}=B{D}^{2}+A{D}^{2}-2BD\cdot AD \cos \mathrm{\angle }ADB={m}^{2}+4+2m $ .
在 $ △ACD $ 中, $ A{C}^{2}=C{D}^{2}+A{D}^{2}-2CD\cdot AD \cos \mathrm{\angle }ADC=4{m}^{2}+4-4m $ ,
所以 $ \dfrac{A{C}^{2}}{A{B}^{2}}=\dfrac{4{m}^{2}+4-4m}{{m}^{2}+4+2m}=\dfrac{4({m}^{2}+4+2m)-12(1+m)}{{m}^{2}+4+2m}=4-\dfrac{12}{(m+1)+\dfrac{3}{m+1}}\geqslant 4-\dfrac{12}{2\sqrt{(m+1)\cdot \dfrac{3}{m+1}}}=4-2\sqrt{3} $ ,
当且仅当 $ m+1=\dfrac{3}{m+1} $ ,即 $ m=\sqrt{3}-1 $ 时,等号成立,
所以当 $ \dfrac{AC}{AB} $ 取最小值时, $ m=\sqrt{3}-1 $ .
16.记 $ △ABC $ 的内角 $ A $ , $ B $ , $ C $ 的对边分别为 $ a $ , $ b $ , $ c $ .已知 $ \sin C=\sqrt{2} \cos B $ , $ {a}^{2}+{b}^{2}-{c}^{2}=\sqrt{2}ab $ .
(1) 求 $ B $ ;
(2) 若 $ △ABC $ 的面积为 $ 3+\sqrt{3} $ ,求 $ c $ .
答案:(1) 【解】已知 $ {a}^{2}+{b}^{2}-{c}^{2}=\sqrt{2}ab $ ,则有 $ \cos C=\dfrac{{a}^{2}+{b}^{2}-{c}^{2}}{2ab}=\dfrac{\sqrt{2}}{2} $ .
又 $ C\in (0,\mathrm{\pi }) $ ,所以 $ C=\dfrac{\mathrm{\pi }}{4} $ .
又 $ \sin C=\sqrt{2} \cos B $ ,所以 $ \cos B=\dfrac{ \sin C}{\sqrt{2}}=\dfrac{1}{2} $ .
又 $ B\in (0,\mathrm{\pi }) $ ,所以 $ B=\dfrac{\mathrm{\pi }}{3} $ .
(2) 由(1)可得 $ C=\dfrac{\mathrm{\pi }}{4} $ , $ B=\dfrac{\mathrm{\pi }}{3} $ ,由正弦定理,不妨令 $ \dfrac{c}{ \sin C}=\dfrac{b}{ \sin B}=k(k > 0) $ ,则有 $ c=\dfrac{\sqrt{2}}{2}k $ , $ b=\dfrac{\sqrt{3}}{2}k $ .
又 $ {S}_{△ABC}=3+\sqrt{3} $ ,
所以 $ {S}_{△ABC}=\dfrac{1}{2}bc \sin A=\dfrac{1}{2}bc \sin (B+C)=\dfrac{1}{2}\cdot \dfrac{\sqrt{2}}{2}k\cdot \dfrac{\sqrt{3}}{2}k( \sin B \cos C+ \cos B \sin C)=\dfrac{\sqrt{6}}{8}{k}^{2}(\dfrac{\sqrt{3}}{2}×\dfrac{\sqrt{2}}{2}+\dfrac{1}{2}×\dfrac{\sqrt{2}}{2})=\dfrac{\sqrt{6}}{8}{k}^{2}\cdot \dfrac{\sqrt{6}+\sqrt{2}}{4}=3+\sqrt{3} $ ,解得 $ k=4 $ (负值舍去),故 $ c=\dfrac{\sqrt{2}}{2}k=2\sqrt{2} $ .
解析:
17.在 $ △ABC $ 中, $ \cos A=-\dfrac{1}{3} $ , $ a \sin C=4\sqrt{2} $ .
(1) 求 $ c $ 的值;
(2) 再从条件①、条件②、条件③这三个条件中选择一个作为已知,使得 $ △ABC $ 存在,求 $ BC $ 边上的高.
条件①: $ a=6 $ ;条件②: $ a \sin B=\dfrac{10\sqrt{2}}{3} $ ;
条件③: $ △ABC $ 的面积为 $ 10\sqrt{2} $ .
注:如果选择的条件不符合要求,第(2)问得0分,如果选择多个符合要求的条件分别解答,按第一个解答计分.
答案:(1) 【解】在 $ △ABC $ 中, $ A\in (0,\mathrm{\pi }) $ , $ \cos A=-\dfrac{1}{3} $ ,
又 $ { \sin }^{2}A+{ \cos }^{2}A=1 $ , $ \therefore \sin A=\dfrac{2\sqrt{2}}{3} $ .
由正弦定理得 $ \dfrac{a}{ \sin A}=\dfrac{c}{ \sin C} $ ,
$ \therefore a \sin C=c \sin A=4\sqrt{2} $ , $ \therefore c=6 $ .
(2) 选条件①.
$ \because △ABC $ 中, $ \cos A=-\dfrac{1}{3} < 0 $ , $ \therefore A\in (\dfrac{\mathrm{\pi }}{2},\mathrm{\pi }) $ .
$ \because a=c=6 $ , $ \therefore △ABC $ 是等腰三角形,且 $ A=C $ ,
此时 $ △ABC $ 内角和大于 $ \mathrm{\pi } $ ,即 $ △ABC $ 不存在,故不选条件①.
选条件②.
$ \because a \sin B=b \sin A=\dfrac{10\sqrt{2}}{3} $ , $ \sin A=\dfrac{2\sqrt{2}}{3} $ ,
$ \therefore b=5 $ .
由(1)知 $ c=6 $ ,则由余弦定理可得
$ {6}^{2}+{5}^{2}-{a}^{2}=2×5×6×(-\dfrac{1}{3}) $ ,
$ \therefore a=9 $ (负值舍去),
$ \therefore 9 \sin C=4\sqrt{2} $ , $ \therefore \sin C=\dfrac{4\sqrt{2}}{9} $ .
设 $ BC $ 边上的高为 $ ℎ $ , $ \therefore ℎ=b \sin C=5×\dfrac{4\sqrt{2}}{9}=\dfrac{20\sqrt{2}}{9} $ .
选条件③.
$ \because {S}_{△ABC}=\dfrac{1}{2}bc \sin A=10\sqrt{2} $ , $ c=6 $ ,
$ \therefore b=5 $ .
在 $ △ABC $ 中,由余弦定理得 $ \cos A=\dfrac{{b}^{2}+{c}^{2}-{a}^{2}}{2bc}=-\dfrac{1}{3} $ ,解得 $ a=9 $ (负值舍去).
设 $ BC $ 边上的高为 $ ℎ $ ,则 $ {S}_{△ABC}=\dfrac{1}{2}aℎ=10\sqrt{2} $ ,解得 $ ℎ=\dfrac{20\sqrt{2}}{9} $ .
解析:
18.记 $ △ABC $ 的内角 $ A $ , $ B $ , $ C $ 的对边分别为 $ a $ , $ b $ , $ c $ ,已知 $ \sin A+\sqrt{3} \cos A=2 $ .
(1) 求 $ A $ ;
(2) 若 $ a=2 $ , $ \sqrt{2}b \sin C=c \sin 2B $ ,求 $ △ABC $ 的周长.
答案:(1) 【解】由 $ \sin A+\sqrt{3} \cos A=2 $ ,得 $ 2(\dfrac{1}{2} \sin A+\dfrac{\sqrt{3}}{2} \cos A)=2 $ ,
所以 $ \sin (A+\dfrac{\mathrm{\pi }}{3})=1 $ .
由 $ A\in (0,\mathrm{\pi }) $ ,得 $ A+\dfrac{\mathrm{\pi }}{3}\in (\dfrac{\mathrm{\pi }}{3},\dfrac{4\mathrm{\pi }}{3}) $ ,所以 $ A+\dfrac{\mathrm{\pi }}{3}=\dfrac{\mathrm{\pi }}{2} $ ,
所以 $ A=\dfrac{\mathrm{\pi }}{6} $ .
(2) 由 $ A $ , $ B $ , $ C $ 为三角形内角,得 $ \sin B\ne 0 $ , $ \sin C\ne 0 $ .
因为 $ \sqrt{2}b \sin C=c \sin 2B $ ,
所以由正弦定理得 $ \sqrt{2} \sin B \sin C= \sin C \sin 2B $ ,
所以 $ \sqrt{2} \sin B= \sin 2B $ ,即 $ \sqrt{2} \sin B=2 \sin B \cos B $ ,
所以 $ \cos B=\dfrac{\sqrt{2}}{2} $ ,所以 $ B=\dfrac{\mathrm{\pi }}{4} $ .
因为 $ a=2 $ , $ A=\dfrac{\mathrm{\pi }}{6} $ ,所以由正弦定理,得 $ b=\dfrac{a}{ \sin A} \sin B=2\sqrt{2} $ .
由 $ A=\dfrac{\mathrm{\pi }}{6} $ , $ B=\dfrac{\mathrm{\pi }}{4} $ ,得 $ C=\dfrac{7\mathrm{\pi }}{12} $ ,所以 $ \sin C= \sin \dfrac{7\mathrm{\pi }}{12}= \sin (\dfrac{\mathrm{\pi }}{3}+\dfrac{\mathrm{\pi }}{4})=\dfrac{\sqrt{2}}{2}×\dfrac{\sqrt{3}}{2}+\dfrac{\sqrt{2}}{2}×\dfrac{1}{2}=\dfrac{\sqrt{6}+\sqrt{2}}{4} $ ,
所以由正弦定理,得 $ c=\dfrac{a \sin C}{ \sin A}=\dfrac{2×\dfrac{\sqrt{6}+\sqrt{2}}{4}}{\dfrac{1}{2}}=\sqrt{6}+\sqrt{2} $ ,
所以 $ △ABC $ 的周长为 $ a+b+c=2+2\sqrt{2}+\sqrt{6}+\sqrt{2}=2+\sqrt{6}+3\sqrt{2} $ .
解析:
19.记 $ △ABC $ 的内角 $ A $ , $ B $ , $ C $ 的对边分别为 $ a $ , $ b $ , $ c $ ,已知 $ \dfrac{ \cos A}{1+ \sin A}=\dfrac{ \sin 2B}{1+ \cos 2B} $ .
(1) 若 $ C=\dfrac{2\mathrm{\pi }}{3} $ ,求 $ B $ ;
(2) 求 $ \dfrac{{a}^{2}+{b}^{2}}{{c}^{2}} $ 的最小值.
答案:(1) 【解】因为 $ \dfrac{ \cos A}{1+ \sin A}=\dfrac{ \sin 2B}{1+ \cos 2B}=\dfrac{2 \sin B \cos B}{2{ \cos }^{2}B}=\dfrac{ \sin B}{ \cos B}( \cos B\ne 0) $ ,
所以 $ \cos A \cos B= \sin B+ \sin A \sin B $ ,即 $ \cos (A+B)= \sin B $ ,即 $ \cos (\mathrm{\pi }-C)=- \cos C= \sin B $ ,
所以当 $ C=\dfrac{2\mathrm{\pi }}{3} $ 时, $ \sin B=- \cos \dfrac{2\mathrm{\pi }}{3}=\dfrac{1}{2} $ .
又 $ 0 < B < \dfrac{\mathrm{\pi }}{3} $ ,所以 $ B=\dfrac{\mathrm{\pi }}{6} $ .
(2) 由(1)知, $ \sin B=- \cos C $ ,所以 $ B=C-\dfrac{\mathrm{\pi }}{2} $ ,所以 $ \cos B= \sin C(\dfrac{\mathrm{\pi }}{2} < C < \mathrm{\pi }) $ .
由正弦定理得 $ \dfrac{{a}^{2}+{b}^{2}}{{c}^{2}}=\dfrac{{ \sin }^{2}A+{ \sin }^{2}B}{{ \sin }^{2}C}=\dfrac{{ \sin }^{2}A+{ \cos }^{2}C}{{ \sin }^{2}C}=\dfrac{{ \sin }^{2}(B+C)+{ \cos }^{2}C}{{ \sin }^{2}C} $
$ =\dfrac{1}{{ \sin }^{2}C}({ \sin }^{2}B{ \cos }^{2}C+{ \cos }^{2}B{ \sin }^{2}C+2 \sin B\cdot \cos B \sin C \cos C+{ \cos }^{2}C) $
$ =\dfrac{{ \cos }^{4}C+{ \sin }^{4}C-2{ \sin }^{2}C{ \cos }^{2}C+{ \cos }^{2}C}{{ \sin }^{2}C} $
$ =\dfrac{1}{{ \sin }^{2}C} [ (1-{ \sin }^{2}C)^{2}+{ \sin }^{4}C-2{ \sin }^{2}C\cdot (1-{ \sin }^{2}C )+1-{ \sin }^{2}C ] $
$ =\dfrac{4{ \sin }^{4}C-5{ \sin }^{2}C+2}{{ \sin }^{2}C} $
$ =4{ \sin }^{2}C+\dfrac{2}{{ \sin }^{2}C}-5\geqslant 4\sqrt{2}-5 $ ,
当且仅当 $ { \sin }^{4}C=\dfrac{1}{2}(\dfrac{\mathrm{\pi }}{2} < C < \mathrm{\pi }) $ 时取等号.故 $ \dfrac{{a}^{2}+{b}^{2}}{{c}^{2}} $ 的最小值为 $ 4\sqrt{2}-5 $ .
解析:
20.魏晋时期刘徽撰写的《海岛算经》是关于测量的数学著作,其中第一题是测量海岛的高.如图,点 $ E $ , $ H $ , $ G $ 在水平线 $ AC $ 上, $ DE $ 和 $ FG $ 是两个垂直于水平面且等高的测量标杆的高度,称为“表高”, $ EG $ 称为“表距”, $ GC $ 和 $ EH $ 都称为“表目距”, $ GC $ 与 $ EH $ 的差称为“表目距的差”,则海岛的高 $ AB= $ ( )

A. $ \dfrac{表高×表距}{表目距的差}+ $ 表高
B. $ \dfrac{表高×表距}{表目距的差}- $ 表高
C. $ \dfrac{表高×表距}{表目距的差}+ $ 表距
D. $ \dfrac{表高×表距}{表目距的差}- $ 表距
答案:A
解析:过点 $ D $ 作 $ DM//AC $ ,交 $ AB $ 于点 $ M $ .由题意可得 $ D $ , $ F $ , $ M $ 三点共线.设 $ \mathrm{\angle }DHE=\alpha $ , $ \mathrm{\angle }FCG=\beta $ ,则 $ \mathrm{\angle }BDM=\alpha $ , $ \mathrm{\angle }BFM=\beta $ .因为 $ \dfrac{BM}{MD}= \tan \alpha $ , $ \dfrac{BM}{MF}= \tan \beta $ ,所以 $ \dfrac{BM}{ \tan \alpha }=MD $ , $ \dfrac{BM}{ \tan \beta }=MF $ ,两式作差可得 $ \dfrac{BM}{ \tan \beta }-\dfrac{BM}{ \tan \alpha }=MF-MD=DF=EG $ ,所以 $ BM=\dfrac{EG}{\dfrac{1}{ \tan \beta }-\dfrac{1}{ \tan \alpha }}=\dfrac{EG}{\dfrac{GC}{FG}-\dfrac{EH}{DE}} $ .又因为 $ DE=FG $ ,所以 $ BM=\dfrac{EG\cdot DE}{GC-EH} $ ,所以海岛的高 $ AB=AM+BM=AM+\dfrac{EG\cdot DE}{GC-EH}=DE+\dfrac{EG\cdot DE}{GC-EH} $ .故选 $ \mathrm{A} $ .
二、刷原创
1.已知向量 $ \boldsymbol{a} $ 与 $ \boldsymbol{b} $ , $ |\boldsymbol{a}|=4 $ , $ |\boldsymbol{b}|=2 $ ,向量 $ \boldsymbol{a} $ 在向量 $ \boldsymbol{b} $ 上的投影向量是 $ -\dfrac{1}{2}\boldsymbol{b} $ ,则 $ |\boldsymbol{a}+\boldsymbol{b}|= $ ( )
A.4
B.16
C.1
D.3
答案:A
解析:因为 $ |\boldsymbol{a}|=4 $ , $ |\boldsymbol{b}|=2 $ ,所以向量 $ \boldsymbol{a} $ 在向量 $ \boldsymbol{b} $ 上的投影向量是 $ \dfrac{\boldsymbol{a}\cdot \boldsymbol{b}}{|\boldsymbol{b}|}\cdot \dfrac{\boldsymbol{b}}{|\boldsymbol{b}|}=\dfrac{\boldsymbol{a}\cdot \boldsymbol{b}}{2}\cdot \dfrac{\boldsymbol{b}}{2}=-\dfrac{1}{2}\boldsymbol{b} $ ,所以 $ \boldsymbol{a}\cdot \boldsymbol{b}=-2 $ ,所以 $ |\boldsymbol{a}+\boldsymbol{b}|=\sqrt{{\boldsymbol{a}}^{2}+{\boldsymbol{b}}^{2}+2\boldsymbol{a}\cdot \boldsymbol{b}}=\sqrt{16+4-4}=4 $ .故选 $ \mathrm{A} $ .
2.已知向量 $ \boldsymbol{a}=(2,1) $ , $ \boldsymbol{b}=( \cos \alpha ,- \sin \alpha ) $ ,且 $ \boldsymbol{a}\perp \boldsymbol{b} $ ,则 $ \sin 2\alpha +{ \cos }^{2}\alpha = $ .
解析:因为 $ \boldsymbol{a}=(2,1) $ , $ \boldsymbol{b}=( \cos \alpha ,- \sin \alpha ) $ ,且 $ \boldsymbol{a}\perp \boldsymbol{b} $ ,所以 $ \boldsymbol{a}\cdot \boldsymbol{b}=0 $ ,即 $ 2 \cos \alpha - \sin \alpha =0 $ ,所以 $ \tan \alpha =\dfrac{ \sin \alpha }{ \cos \alpha }=2 $ ,所以 $ \sin 2\alpha +{ \cos }^{2}\alpha =\dfrac{2 \sin \alpha \cos \alpha +{ \cos }^{2}\alpha }{{ \sin }^{2}\alpha +{ \cos }^{2}\alpha }=\dfrac{2 \tan \alpha +1}{{ \tan }^{2}\alpha +1}=1 $ .
3.已知点 $ A $ 是半径 $ r=4 $ 的圆 $ O $ 内一点, $ OA=2 $ , $ B $ , $ C $ 为圆 $ O $ 上任意两点,则当 $ \overrightarrow {AC}\cdot \overrightarrow {BC} $ 取得最大值时, $ |\overrightarrow {AB}|= $ .
解析:如图,连接 $ OC $ ,设 $ \theta $ 为 $ \overrightarrow {OA} $ 和 $ \overrightarrow {BC} $ 的夹角,
则 $ \overrightarrow {AC}\cdot \overrightarrow {BC}=(\overrightarrow {OC}-\overrightarrow {OA})\cdot \overrightarrow {BC}=\overrightarrow {OC}\cdot \overrightarrow {BC}-\overrightarrow {OA}\cdot \overrightarrow {BC}=|\overrightarrow {OC}|\cdot |\overrightarrow {BC}| \cos \mathrm{\angle }BCO-|\overrightarrow {OA}|\cdot |\overrightarrow {BC}| \cos \theta =\dfrac{1}{2}{|\overrightarrow {BC}|}^{2}-2|\overrightarrow {BC}| \cos \theta $ ,
又 $ \dfrac{1}{2}{|\overrightarrow {BC}|}^{2}-2|\overrightarrow {BC}|\leqslant \dfrac{1}{2}{|\overrightarrow {BC}|}^{2}-2|\overrightarrow {BC}|\cdot \cos \theta \leqslant \dfrac{1}{2}{|\overrightarrow {BC}|}^{2}+2|\overrightarrow {BC}| $ ,
即 $ \dfrac{1}{2}{\left(|\overrightarrow {BC}|-2\right) ^ {2}}-2\leqslant \dfrac{1}{2}{|\overrightarrow {BC}|}^{2}-2|\overrightarrow {BC}|\cdot \cos \theta \leqslant \dfrac{1}{2}{\left(|\overrightarrow {BC}|+2\right) ^ {2}}-2 $ .
由 $ |\overrightarrow {BC}|\in [0,8] $ ,可知当 $ |\overrightarrow {BC}|=8 $ 时, $ \overrightarrow {AC}\cdot \overrightarrow {BC} $ 有最大值48,此时 $ \cos \theta =-1 $ , $ \theta =\mathrm{\pi } $ , $ B $ , $ A $ , $ O $ , $ C $ 四点共线,且点 $ A $ 在线段 $ BO $ 上,所以 $ AB=4-2=2 $ ,即 $ |\overrightarrow {AB}|=2 $ .
4.在 $ △ABC $ 中, 内角 $ A $ , $ B $ , $ C $ 的对边分别为 $ a $ , $ b $ , $ c $ , $ \mathrm{\angle }ABC $ 的平分线交 $ AC $ 于点 $ D $ , $ BD=2 $ ,若 $ 9a+c $ 的最小值为32,则 $ \tan \mathrm{\angle }ABC= $ ( )
A. $ -\sqrt{3} $
B. $ \sqrt{3} $
C. $ \sqrt{7} $
D.2
答案:A
解析:设 $ \mathrm{\angle }ABC=2\theta (0 < \theta < \dfrac{\mathrm{\pi }}{2}) $ ,由 $ {S}_{△ABC}={S}_{△ABD}+{S}_{△BCD} $ ,角平分线性质和三角形面积公式得,
$ \dfrac{1}{2}ac \sin 2\theta =\dfrac{1}{2}\cdot 2a \sin \theta +\dfrac{1}{2}\cdot 2c \sin \theta $ ,即 $ 2ac \sin \theta \cdot \cos \theta =2(a+c) \sin \theta $ ,整理可得 $ \dfrac{1}{a}+\dfrac{1}{c}= \cos \theta $ ,则 $ 9a+c=\dfrac{1}{ \cos \theta }\cdot (9a+c)(\dfrac{1}{a}+\dfrac{1}{c})=\dfrac{1}{ \cos \theta }(\dfrac{c}{a}+\dfrac{9a}{c}+10)\geqslant \dfrac{1}{ \cos \theta }(2\sqrt{\dfrac{c}{a}\cdot \dfrac{9a}{c}}+10)=\dfrac{16}{ \cos \theta } $ ,当且仅当 $ \dfrac{c}{a}=\dfrac{9a}{c} $ ,即 $ c=3a $ 时取等号,即 $ \dfrac{16}{ \cos \theta }=32 $ ,所以 $ \cos \theta =\dfrac{1}{2} $ .又 $ 0 < \theta < \dfrac{\mathrm{\pi }}{2} $ ,所以 $ \theta =\dfrac{\mathrm{\pi }}{3} $ ,所以 $ \tan \mathrm{\angle }ABC= \tan \dfrac{2\mathrm{\pi }}{3}=-\sqrt{3} $ .故选 $ \mathrm{A} $ .
5.在 $ △ABC $ 中,内角 $ A $ , $ B $ , $ C $ 所对的边分别为 $ a $ , $ b $ , $ c $ , $ B=\dfrac{\mathrm{\pi }}{3} $ , $ a=4 $ ,则下列说法正确的是( )(多选)
A.若 $ b=2\sqrt{3} $ ,则 $ △ABC $ 为直角三角形
B. $ △ABC $ 的中线 $ BD $ 有最小值
C.若 $ \mathrm{\angle }ABC $ 的平分线 $ BD $ 长为 $ \sqrt{3} $ ,则 $ c=\dfrac{4}{3} $
D.当 $ △ABC $ 为锐角三角形时, $ b $ 的取值范围是 $ (\sqrt{3},2\sqrt{3}) $
答案:AC
解析:对于 $ \mathrm{A} $ ,由正弦定理得 $ \dfrac{a}{ \sin A}=\dfrac{b}{ \sin B} $ ,则 $ \sin A=\dfrac{a \sin B}{b}=1 $ ,因为 $ A\in (0,\mathrm{\pi }) $ ,所以 $ A=\dfrac{\mathrm{\pi }}{2} $ ,故 $ \mathrm{A} $ 正确;
对于 $ \mathrm{B} $ ,由题知 $ \overrightarrow {BD}=\dfrac{1}{2}(\overrightarrow {BA}+\overrightarrow {BC}) $ ,则 $ {\overrightarrow {BD}}^{2}=\dfrac{1}{4}({c}^{2}+{a}^{2}+2ac \cos \mathrm{\angle }ABC)=\dfrac{1}{4}({c}^{2}+16+4c) > 4 $ ,没有最小值,故 $ \mathrm{B} $ 错误;
对于 $ \mathrm{C} $ ,由 $ {S}_{△ABC}={S}_{△BCD}+{S}_{△ABD} $ 及角平分线的性质得 $ \dfrac{1}{2}ac \sin \dfrac{\mathrm{\pi }}{3}=\dfrac{1}{2}a\cdot BD \sin \dfrac{\mathrm{\pi }}{6}+\dfrac{1}{2}c\cdot BD \sin \dfrac{\mathrm{\pi }}{6} $ ,则 $ \sqrt{3}c=\sqrt{3}+\dfrac{\sqrt{3}}{4}c $ ,解得 $ c=\dfrac{4}{3} $ ,故 $ \mathrm{C} $ 正确;
对于 $ \mathrm{D} $ ,因为 $ B=\dfrac{\mathrm{\pi }}{3} $ ,所以 $ C=\mathrm{\pi }-A-B=\dfrac{2\mathrm{\pi }}{3}-A $ ,当 $ △ABC $ 为锐角三角形时, $ \begin{cases}0 < A < \dfrac{\mathrm{\pi }}{2},\\ 0 < \dfrac{2\mathrm{\pi }}{3}-A < \dfrac{\mathrm{\pi }}{2},\end{cases} $ 解得 $ \dfrac{\mathrm{\pi }}{6} < A < \dfrac{\mathrm{\pi }}{2} $ ,则 $ \dfrac{1}{2} < \sin A < 1 $ ,
由正弦定理得 $ \dfrac{a}{ \sin A}=\dfrac{b}{ \sin B} $ ,则 $ b=\dfrac{a \sin B}{ \sin A}=\dfrac{2\sqrt{3}}{ \sin A}\in (2\sqrt{3},4\sqrt{3}) $ ,故 $ \mathrm{D} $ 错误.故选 $ \mathrm{A}\mathrm{C} $ .
6.已知在锐角三角形 $ ABC $ 中,内角 $ A $ , $ B $ , $ C $ 所对的边分别为 $ a $ , $ b $ , $ c $ , $ 2{a}^{2} \cos A={b}^{2}-{c}^{2} $ ,若 $ ct{ \cos }^{2}C > b $ 恒成立,则实数 $ t $ 的最小值为 .
解析:由 $ 2{a}^{2} \cos A={b}^{2}-{c}^{2} $ 得, $ \dfrac{{b}^{2}-{c}^{2}}{{a}^{2}}=2 \cos A $ ,所以 $ \dfrac{{a}^{2}+{c}^{2}-2ac\cdot \cos B-{c}^{2}}{{a}^{2}}=2 \cos A $ ,所以 $ \dfrac{a-2c\cdot \cos B}{a}=2 \cos A $ ,由正弦定理可得 $ \sin A-2 \sin C \cos B=2 \sin A \cos A $ .在 $ △ABC $ 中,因为 $ \sin A= \sin (\mathrm{\pi }-B-C)= \sin (B+C)= \sin B \cos C+ \cos B \sin C $ ,
所以 $ \sin B \cos C- \cos B \sin C=2 \sin A\cdot \cos A $ ,即 $ \sin (B-C)= \sin 2A $ .
①当 $ B-C=2A $ 时,由 $ A+B+C=\mathrm{\pi } $ ,得 $ 2B=\mathrm{\pi }+A > \mathrm{\pi } $ , $ B > \dfrac{\mathrm{\pi }}{2} $ ,又 $ △ABC $ 是锐角三角形,所以不成立;
②当 $ B-C+2A=\mathrm{\pi } $ 时,由 $ A+B+C=\mathrm{\pi } $ ,得 $ A=2C $ , $ B=\mathrm{\pi }-3C $ ,又 $ △ABC $ 是锐角三角形,所以 $ \begin{cases}0 < A < \dfrac{\mathrm{\pi }}{2},\\ 0 < B < \dfrac{\mathrm{\pi }}{2},\end{cases} $ 得 $ \dfrac{\mathrm{\pi }}{6} < C < \dfrac{\mathrm{\pi }}{4} $ .
由 $ ct{ \cos }^{2}C > b $ 恒成立,得 $ t > \dfrac{b}{c{ \cos }^{2}C} $ 恒成立, $ \dfrac{b}{c{ \cos }^{2}C}=\dfrac{ \sin B}{ \sin C{ \cos }^{2}C}=\dfrac{2 \sin 3C}{ \sin 2C \cos C} $
$ =\dfrac{2 \sin (2C+C)}{ \sin 2C \cos C} $
$ =\dfrac{2( \sin 2C \cos C+ \cos 2C \sin C)}{ \sin 2C \cos C} $
$ =2+\dfrac{2 \cos 2C \sin C}{ \sin 2C \cos C} $
$ =2+\dfrac{2(2{ \cos }^{2}C-1) \sin C}{2 \sin C{ \cos }^{2}C}=4-\dfrac{1}{{ \cos }^{2}C} $ ,
又 $ \dfrac{\sqrt{2}}{2} < \cos C < \dfrac{\sqrt{3}}{2} $ ,则 $ { \cos }^{2}C\in (\dfrac{1}{2},\dfrac{3}{4}) $ ,
所以 $ 4-\dfrac{1}{{ \cos }^{2}C}\in (2,\dfrac{8}{3}) $ ,即 $ \dfrac{b}{c{ \cos }^{2}C}\in (2,\dfrac{8}{3}) $ ,所以 $ t\geqslant \dfrac{8}{3} $ ,所以实数 $ t $ 的最小值为 $ \dfrac{8}{3} $ .
7.在锐角三角形 $ ABC $ 中,内角 $ A $ , $ B $ , $ C $ 所对的边分别为 $ a $ , $ b $ , $ c $ , $ \dfrac{ \sin C}{ \sin B}=\dfrac{2b}{c}+ \cos A $ .
(1) 求证: $ { \sin }^{2}A+{ \sin }^{2}C=5{ \sin }^{2}B $ ;
(2) 求 $ \cos 2B $ 的取值范围.
答案:(1) 【证明】由 $ \dfrac{ \sin C}{ \sin B}=\dfrac{2b}{c}+ \cos A $ 及正弦定理得 $ \dfrac{c}{b}=\dfrac{2b}{c}+ \cos A $ ,所以 $ {c}^{2}-bc \cos A-2{b}^{2}=0 $ ,
由余弦定理得 $ \cos A=\dfrac{{b}^{2}+{c}^{2}-{a}^{2}}{2bc} $ ,所以 $ {c}^{2}-bc\cdot \dfrac{{b}^{2}+{c}^{2}-{a}^{2}}{2bc}-2{b}^{2}=0 $ ,整理得 $ 5{b}^{2}={c}^{2}+{a}^{2} $ ,
所以由正弦定理得 $ { \sin }^{2}A+{ \sin }^{2}C=5{ \sin }^{2}B $ .
(2) 【解】因为 $ △ABC $ 为锐角三角形,
所以 $ \begin{cases} \cos A=\dfrac{{b}^{2}+{c}^{2}-{a}^{2}}{2bc} > 0,\\ \cos B=\dfrac{{a}^{2}+{c}^{2}-{b}^{2}}{2ac} > 0,\\ \cos C=\dfrac{{b}^{2}+{a}^{2}-{c}^{2}}{2ab} > 0,\end{cases} $
则有 $ {b}^{2}+{a}^{2} > {c}^{2} $ , $ {b}^{2}+{c}^{2} > {a}^{2} $ , $ {a}^{2}+{c}^{2} > {b}^{2} $ .
由(1)得 $ 5{b}^{2}={c}^{2}+{a}^{2} $ ,所以 $ 3{a}^{2} > 2{c}^{2} $ , $ 3{c}^{2} > 2{a}^{2} $ ,所以 $ \dfrac{2}{3} < \dfrac{{c}^{2}}{{a}^{2}} < \dfrac{3}{2} $ ,即 $ \dfrac{\sqrt{6}}{3} < \dfrac{c}{a} < \dfrac{\sqrt{6}}{2} $ ,
所以 $ \cos B=\dfrac{{a}^{2}+{c}^{2}-{b}^{2}}{2ac}=\dfrac{{a}^{2}+{c}^{2}-\dfrac{1}{5}({a}^{2}+{c}^{2})}{2ac}=\dfrac{2}{5}(\dfrac{c}{a}+\dfrac{a}{c}) $ .
令 $ t=\dfrac{c}{a} $ ,则 $ \dfrac{\sqrt{6}}{3} < t < \dfrac{\sqrt{6}}{2} $ ,
所以 $ \cos B=\dfrac{2}{5}(t+\dfrac{1}{t}) $ ,令 $ f(t)=t+\dfrac{1}{t} $ ,则 $ f(t) $ 在 $ (\dfrac{\sqrt{6}}{3},1) $ 上单调递减,在 $ (1,\dfrac{\sqrt{6}}{2}) $ 上单调递增,又 $ f(1)=2 $ , $ f(\dfrac{\sqrt{6}}{3})=f(\dfrac{\sqrt{6}}{2})=\dfrac{5\sqrt{6}}{6} $ ,
所以 $ 2\leqslant t+\dfrac{1}{t} < \dfrac{5\sqrt{6}}{6} $ ,所以 $ \dfrac{4}{5}\leqslant \cos B < \dfrac{\sqrt{6}}{3} $ ,即 $ \cos B $ 的取值范围为 $ [\dfrac{4}{5},\dfrac{\sqrt{6}}{3}) $ .
所以 $ \cos 2B=2{ \cos }^{2}B-1\in [\dfrac{7}{25},\dfrac{1}{3}) $ .
故 $ \cos 2B $ 的取值范围为 $ [\dfrac{7}{25},\dfrac{1}{3}) $ .
解析:








