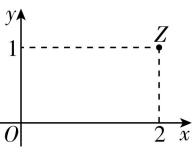
1.如图,在复平面内,复数 $ z $ 对应的点 $ Z $ 如图所示,则复数 $ z= $ ( )
A. $ 1-2\mathrm{i} $
B. $ 2-\mathrm{i} $
C. $ 1+2\mathrm{i} $
D. $ 2+\mathrm{i} $
复数 $ z $ 对应的点 $ Z $ 的坐标为 $ (2,1) $ ,则复数 $ z=2+\mathrm{i} $ .故选 $ \mathrm{D} $ .
1.如图,在复平面内,复数 $ z $ 对应的点 $ Z $ 如图所示,则复数 $ z= $ ( )

A. $ 1-2\mathrm{i} $
B. $ 2-\mathrm{i} $
C. $ 1+2\mathrm{i} $
D. $ 2+\mathrm{i} $
复数 $ z $ 对应的点 $ Z $ 的坐标为 $ (2,1) $ ,则复数 $ z=2+\mathrm{i} $ .故选 $ \mathrm{D} $ .
2.在复平面内,复数 $ z=({a}^{2}-2a)+({a}^{2}-a-2)\mathrm{i}(a\in \boldsymbol{R}) $ 对应的点在虚轴上,则( )
A. $ a=0 $ 或 $ a=2 $
B. $ a=0 $
C. $ a\ne 1 $ 且 $ a\ne 2 $
D. $ a\ne 1 $ 或 $ a\ne 2 $
$ \because $ 复数 $ z=({a}^{2}-2a)+({a}^{2}-a-2)\mathrm{i}(a\in \boldsymbol{R}) $ 对应的点在虚轴上, $ \therefore {a}^{2}-2a=0 $ , $ \therefore a=0 $ 或 $ a=2 $ .故选 $ \mathrm{A} $ .
3.当复平面内表示复数 $ z=({m}^{2}-8m+15)+({m}^{2}-5m-14)\mathrm{i} $ 的点位于第四象限时,实数 $ m $ 的取值范围是( )
A. $ (-2,7) $
B. $ (-2,3)\cup (5,7) $
C. $ (3,5) $
D. $ (5,7) $
由在复平面内表示复数 $ z=({m}^{2}-8m+15)+({m}^{2}-5m-14)\mathrm{i} $ 的点位于第四象限,得 $ \begin{cases}{m}^{2}-8m+15 > 0,\\ {m}^{2}-5m-14 < 0,\end{cases} $ 即 $ \begin{cases}m < 3或m > 5,\\ -2 < m < 7,\end{cases} $ 解得 $ -2 < m < 3 $ 或 $ 5 < m < 7 $ ,即实数 $ m $ 的取值范围是 $ (-2,3)\cup (5,7) $ ,故选 $ \mathrm{B} $ .
4.复数 $ 1-\sqrt{3}\mathrm{i} $ 在复平面内对应的点到原点的距离是 .
2
复数 $ 1-\sqrt{3}\mathrm{i} $ 在复平面内对应的点的坐标为 $ (1,-\sqrt{3}) $ ,所以复数 $ 1-\sqrt{3}\mathrm{i} $ 在复平面内对应的点到原点的距离是 $ \sqrt{{1}^{2}+(-\sqrt{3})^{2}}=2 $ .
5.在复平面内, $ O $ 为坐标原点,向量 $ \overrightarrow {OA} $ 对应的复数为 $ -3-7\mathrm{i} $ ,若点 $ A $ 关于实轴的对称点为 $ B $ ,则向量 $ \overrightarrow {OB} $ 对应的复数为( )
A. $ 7+3\mathrm{i} $
B. $ 3+7\mathrm{i} $
C. $ 3-7\mathrm{i} $
D. $ -3+7\mathrm{i} $
依题意,点 $ A $ 在复平面内的坐标为 $ (-3,-7) $ ,则点 $ A $ 关于实轴对称的点 $ B $ 的坐标为 $ (-3,7) $ ,所以向量 $ \overrightarrow {OB} $ 对应的复数为 $ -3+7\mathrm{i} $ .故选 $ \mathrm{D} $ .
6.在复平面内,平行四边形 $ ABCD $ 的3个顶点 $ A $ , $ B $ , $ C $ 对应的复数分别是 $ 1+2\mathrm{i} $ , $ -2+\mathrm{i} {\rm ,0} $ ,则点 $ D $ 对应的复数是( )
A. $ 3-\mathrm{i} $
B. $ -1+3\mathrm{i} $
C. $ 3+\mathrm{i} $
D. $ -3-\mathrm{i} $
由题知,点 $ A(1,2) $ , $ B(-2,1) $ , $ C(0,0) $ .设点 $ D $ 的坐标为 $ (x,y) $ ,则有 $ \overrightarrow {AD}=(x-1,y-2) $ , $ \overrightarrow {BC}=(2,-1) $ .又因为四边形 $ ABCD $ 为平行四边形,所以 $ \overrightarrow {AD}=\overrightarrow {BC} $ ,即 $ \begin{cases}x-1=2,\\ y-2=-1,\end{cases} $ 得 $ \begin{cases}x=3,\\ y=1,\end{cases} $ 所以点 $ D(3,1) $ ,其对应的复数为 $ 3+\mathrm{i} $ .故选 $ \mathrm{C} $ .
7.已知复平面内的点 $ M $ 对应的复数是1,点 $ N $ 对应的复数是 $ \mathrm{i} $ ,则向量 $ \overrightarrow {MN} $ 对应的复数是 .
$ -1+\mathrm{i} $
由题意得, $ M(1,0) $ , $ N(0,1) $ ,则 $ \overrightarrow {MN}=(0,1)-(1,0)=(-1,1) $ ,故 $ \overrightarrow {MN} $ 对应的复数为 $ -1+\mathrm{i} $ .
8.已知复数 $ z $ 在复平面内对应的点为 $ (-2,1) $ ,则 $ |z{|}^{2}= $ ( )
A.3
B. $ 3-4\mathrm{i} $
C. $ 5-4\mathrm{i} $
D.5
由题意可得复数 $ z $ 的实部为 $ -2 $ ,虚部为1,所以 $ |z{|}^{2}=(-2)^{2}+{1}^{2}=5 $ .故选 $ \mathrm{D} $ .
9.已知 $ {z}_{1} $ , $ {z}_{2} $ 为复数,则下列说法不正确的是( )(多选)
A.若 $ {z}_{1}={z}_{2} $ ,则 $ |{z}_{1}|=|{z}_{2}| $
B.若 $ {z}_{1}\ne {z}_{2} $ ,则 $ |{z}_{1}|\ne |{z}_{2}| $
C.若 $ {z}_{1} > {z}_{2} $ ,则 $ |{z}_{1}| > |{z}_{2}| $
D.若 $ |{z}_{1}| > |{z}_{2}| $ ,则 $ {z}_{1} > {z}_{2} $
因为当两个复数相等时,模一定相等,所以 $ \mathrm{A} $ 正确;当两个复数不相等时,它们的模有可能相等,比如 $ 1-\mathrm{i}\ne 1+\mathrm{i} $ ,但 $ |1-\mathrm{i}|=|1+\mathrm{i}| $ ,所以 $ \mathrm{B} $ 不正确;若 $ {z}_{1} > {z}_{2} $ ,则 $ {z}_{1} $ , $ {z}_{2} $ 为实数,当 $ {z}_{1}=1 $ , $ {z}_{2}=-2 $ 时,满足 $ {z}_{1} > {z}_{2} $ ,但 $ |{z}_{1}| < |{z}_{2}| $ ,所以 $ \mathrm{C} $ 不正确;因为两个虚数之间只有等与不等,不能比较大小,模可以比较大小,所以 $ \mathrm{D} $ 不正确.故选 $ \mathrm{B}\mathrm{C}\mathrm{D} $ .
10.设 $ z\in \boldsymbol{C} $ ,在复平面内 $ z $ 对应的点为 $ \mathbf{Z} $ ,那么满足下列条件的点 $ \mathbf{Z} $ 的集合是什么图形?
(1) $ |z|=2 $ ;
(2) $ 2\leqslant |z|\leqslant 3 $ .
(1) 【解】 $ |z|=2 $ ,则复数 $ z $ 对应的向量 $ \overrightarrow {OZ} $ 的模等于2,
即点 $ \mathbf{Z} $ 到原点 $ O $ 的距离等于2,因此满足条件 $ |z|=2 $ 的点 $ \mathbf{Z} $ 的集合是以原点 $ O $ 为圆心,2为半径的圆.
(2) 不等式 $ 2\leqslant |z|\leqslant 3 $ 可化为不等式组 $ \begin{cases}\mid z\mid \leqslant 3,\\ \mid z\mid \geqslant 2.\end{cases} $
不等式 $ |z|\leqslant 3 $ 的解集是圆 $ |z|=3 $ 和该圆内部所有的点构成的集合,
不等式 $ |z|\geqslant 2 $ 的解集是圆 $ |z|=2 $ 和该圆外部所有的点构成的集合,
这两个集合的交集,即上述不等式组的解集,也就是满足条件 $ 2\leqslant |z|\leqslant 3 $ 的点 $ \mathbf{Z} $ 的集合.
所以满足 $ 2\leqslant |z|\leqslant 3 $ 的点 $ \mathbf{Z} $ 的集合是以原点 $ O $ 为圆心,2和3为半径的两圆所夹的圆环,并包括圆环的边界.

11.已知 $ z $ 在复平面内对应的点为 $ (2,-1) $ ,则 $ z $ 的共轭复数 $ \overline{z} $ 在复平面内对应的点为( )
A. $ (-2,1) $
B. $ (-2,-1) $
C. $ (2,1) $
D. $ (2,-1) $
由题意可得 $ z=2-\mathrm{i} $ ,则 $ \overline{z}=2+\mathrm{i} $ ,其在复平面内对应的点为 $ (2,1) $ .故选 $ \mathrm{C} $ .
12.若复数 $ z $ 满足 $ z=1+\mathrm{i}(\mathrm{i} $ 是虚数单位 $ ) $ ,则下列说法不正确的是( )
A.复数 $ z $ 在复平面内对应的点在第一象限
B. $ z $ 的模为 $ \sqrt{2} $
C. $ z $ 的共轭复数为 $ 1-\mathrm{i} $
D.复数 $ z $ 的虚部为 $ \mathrm{i} $
复数 $ z=1+\mathrm{i} $ 在复平面内对应的点为 $ (1,1) $ ,在第一象限,故 $ \mathrm{A} $ 正确;
$ |z|=\sqrt{{1}^{2}+{1}^{2}}=\sqrt{2} $ ,故 $ \mathrm{B} $ 正确;
$ z $ 的共轭复数 $ \overline{z}=1-\mathrm{i} $ ,故 $ \mathrm{C} $ 正确;
复数 $ z $ 的虚部为1,故 $ \mathrm{D} $ 错误.故选 $ \mathrm{D} $ .
13.已知复数 $ z $ 在复平面内对应的点在第二象限,它的模为3,实部是 $ -\sqrt{5} $ ,则 $ \overline{z}= $ .
$ -\sqrt{5}-2\mathrm{i} $
依题意,设 $ z=-\sqrt{5}+y\mathrm{i} $ , $ y > 0 $ ,于是得 $ |z|=\sqrt{{\left(-\sqrt{5}\right) ^ {2}}+{y}^{2}}=3 $ ,解得 $ y=2 $ ,所以 $ \overline{z}=-\sqrt{5}-y\mathrm{i}=-\sqrt{5}-2\mathrm{i} $ .