第7.2节综合训练

由题意得 $ |{z}_{1}|=\sqrt{13} $ , $ |{z}_{2}|=\sqrt{17} $ , $ |{z}_{1}-{z}_{2}|=|-3-\mathrm{i}|=\sqrt{10} $ ,所以 $ |{z}_{2}| > |{z}_{1}| > |{z}_{1}-{z}_{2}| $ .故选 $ \mathrm{A} $ .

因为 $ {z}_{1}+{z}_{2}=a-4+(3+b)\mathrm{i} $ 为实数,所以 $ 3+b=0 $ ,即 $ b=-3 $ .

又 $ {z}_{1}-{z}_{2}=a+4+(3-b)\mathrm{i} $ 为纯虚数,所以 $ \begin{cases}a+4=0,\\ 3-b\ne 0,\end{cases} $ 即 $ a=-4 $ 且 $ b\ne 3 $ .

综上可知 $ \begin{cases}a=-4,\\ b=-3,\end{cases} $ 所以 $ a+b=-7 $ .故选 $ \mathrm{A} $ .

因为 $ z=-{\mathrm{i}}^{2025}+\dfrac{3-4\mathrm{i}}{|3+4\mathrm{i}|}=-\mathrm{i}+\dfrac{3-4\mathrm{i}}{5}=\dfrac{3}{5}-\dfrac{9}{5}\mathrm{i} $ ,所以 $ \overline{z}=\dfrac{3}{5}+\dfrac{9}{5}\mathrm{i} $ ,故 $ \overline{z} $ 的虚部为 $ \dfrac{9}{5} $ .故选 $ \mathrm{B} $ .

令 $ z=a+b\mathrm{i} $ , $ a $ , $ b\in \boldsymbol{R} $ ,则 $ |z|+z=a+\sqrt{{a}^{2}+{b}^{2}}+b\mathrm{i}=5+\sqrt{3}\mathrm{i} $ ,

所以 $ b=\sqrt{3} $ ,且 $ a+\sqrt{{a}^{2}+{b}^{2}}=a+\sqrt{{a}^{2}+3}=5 $ ,即 $ \sqrt{{a}^{2}+3}=5-a $ ,

所以 $ {a}^{2}+3={a}^{2}-10a+25 $ ,可得 $ a=\dfrac{11}{5} $ ,

故 $ z=\dfrac{11}{5}+\sqrt{3}\mathrm{i} $ ,所以 $ z-\overline{z}=\dfrac{11}{5}+\sqrt{3}\mathrm{i}-\dfrac{11}{5}+\sqrt{3}\mathrm{i}=2\sqrt{3}\mathrm{i} $ .故选 $ \mathrm{B} $ .

根据题意得 $ |z|=|({z}_{2}-z)-{z}_{2}|\leqslant |{z}_{2}-z|+|{z}_{2}|=|{z}_{1}-1|+1\leqslant |{z}_{1}|+1+1=3 $ ,

当 $ {z}_{1}=-1 $ , $ {z}_{2}=1 $ , $ z=3 $ 时, $ |{z}_{1}-{z}_{2}|=|{z}_{1}-1|=|{z}_{2}-z|=2 $ ,此时 $ |z|=3 $ ,

所以 $ |z{|}_{ \max }=3 $ .故选 $ \mathrm{B} $ .

取 $ {z}_{1}=\mathrm{i} $ , $ \theta =0 $ ,则 $ {z}_{2}=1 $ , $ ({z}_{1}+{z}_{2})^{2}={\left(\mathrm{i}+1 \right) ^ {2}}=2\mathrm{i} $ , $ |{z}_{1}+{z}_{2}{|}^{2}={|\mathrm{i}+1|}^{2}=2 $ ,则 $ ({z}_{1}+{z}_{2})^{2}\ne |{z}_{1}+{z}_{2}{|}^{2} $ ,故 $ \mathrm{A} $ 错误；

$ {z}_{2}^{2}={\left( \cos \theta +\mathrm{i}\mathrm{s}\mathrm{i}\mathrm{n}\theta \right) ^ {2}}={ \cos }^{2}\theta -{ \sin }^{2}\theta +\mathrm{i}\cdot 2 \sin \theta \cos \theta = \cos 2\theta +\mathrm{i}\cdot \sin 2\theta $ ,

$ \therefore |{z}_{2}^{2}|={ \cos }^{2}2\theta +{ \sin }^{2}2\theta =1 $ ,

则复平面内 $ {z}_{2}^{2} $ 对应的点的集合是半径为1的圆,即单位圆,故 $ \mathrm{B} $ 正确；

$ \because {z}_{1}+{z}_{2}=x+ \cos \theta +\mathrm{i}\cdot (y+ \sin \theta ) $ , $ \overline{{z}_{1}+{z}_{2}}=x+ \cos \theta -\mathrm{i}\cdot (y+ \sin \theta ) $ ,

$ \overline{{z}_{1}}+\overline{{z}_{2}}=x-y\mathrm{i}+ \cos \theta -\mathrm{i}\mathrm{s}\mathrm{i}\mathrm{n}\theta =x+ \cos \theta -\mathrm{i}\cdot (y+ \sin \theta ) $ , $ \therefore \overline{{z}_{1}+{z}_{2}}=\overline{{z}_{1}}+\overline{{z}_{2}} $ ,故 $ \mathrm{C} $ 正确；

由 $ |{z}_{1}-\mathrm{i}|=1 $ 得 $ {z}_{1} $ 在复平面内对应的点到点 $ (0,1) $ 的距离为1,即 $ {z}_{1} $ 在复平面内对应点的集合是以 $ (0,1) $ 为圆心,1为半径的圆,故 $ \mathrm{D} $ 错误.故选 $ \mathrm{B}\mathrm{C} $ .

由题知 $ \mathrm{\Delta }={b}^{2}-4 < 0 $ ,所以方程的根为 $ x=\dfrac{-b±\sqrt{4-{b}^{2}}\mathrm{i}}{2} $ ,不妨设 $ {z}_{1}=-\dfrac{b}{2}+\dfrac{\sqrt{4-{b}^{2}}}{2}\mathrm{i} $ , $ {z}_{2}=-\dfrac{b}{2}-\dfrac{\sqrt{4-{b}^{2}}}{2}\mathrm{i} $ ,可知 $ {\overline{z}}_{1}={z}_{2} $ ,故 $ \mathrm{A} $ 正确；

由一元二次方程根与系数的关系知 $ {z}_{1}\cdot {z}_{2}=1 $ ,所以 $ |{z}_{1}\cdot {z}_{2}|=1 $ ,故 $ \mathrm{C} $ 正确；

$ \dfrac{{z}_{1}}{{z}_{2}}=\dfrac{{z}_{1}^{2}}{{z}_{1}\cdot {z}_{2}}={z}_{1}^{2}=\dfrac{{b}^{2}-2}{2}-\dfrac{b\sqrt{4-{b}^{2}}}{2}\mathrm{i} $ ,因为 $ -2 < b < 2 $ ,所以当 $ b\ne 0 $ 时, $ \dfrac{{z}_{1}}{{z}_{2}}\notin \boldsymbol{R} $ ,故 $ \mathrm{B} $ 错误；

当 $ b=1 $ 时, $ {z}_{1}=-\dfrac{1}{2}+\dfrac{\sqrt{3}}{2}\mathrm{i} $ , $ {z}_{2}=-\dfrac{1}{2}-\dfrac{\sqrt{3}}{2}\mathrm{i} $ ,

所以 $ {z}_{1}^{2}=-\dfrac{1}{2}-\dfrac{\sqrt{3}}{2}\mathrm{i} $ , $ {z}_{1}^{3}=(-\dfrac{1}{2}-\dfrac{\sqrt{3}}{2}\mathrm{i})\cdot (-\dfrac{1}{2}+\dfrac{\sqrt{3}}{2}\mathrm{i})={\left(-\dfrac{1}{2}\right) ^ {2}}-{\left(\dfrac{\sqrt{3}}{2}\mathrm{i}\right) ^ {2}}=\dfrac{1}{4}+\dfrac{3}{4}=1 $ ,

$ {z}_{2}^{2}=-\dfrac{1}{2}+\dfrac{\sqrt{3}}{2}\mathrm{i} $ , $ {z}_{2}^{3}=(-\dfrac{1}{2}+\dfrac{\sqrt{3}}{2}\mathrm{i})\cdot (-\dfrac{1}{2}-\dfrac{\sqrt{3}}{2}\mathrm{i})={\left(-\dfrac{1}{2}\right) ^ {2}}-{\left(\dfrac{\sqrt{3}}{2}\mathrm{i}\right) ^ {2}}=\dfrac{1}{4}+\dfrac{3}{4}=1 $ ,所以 $ {z}_{1}^{3}={z}_{2}^{3}=1 $ ,故 $ \mathrm{D} $ 正确.

故选 $ \mathrm{A}\mathrm{C}\mathrm{D} $ .

设 $ z=a+b\mathrm{i}(a,b\in \boldsymbol{R}) $ ,则 $ \overline{z}=a-b\mathrm{i} $ .因为 $ z+\overline{z}=4 $ ,所以 $ a=2 $ .

又因为 $ z\cdot \overline{z}=8 $ ,所以 $ 4+{b}^{2}=8 $ ,所以 $ {b}^{2}=4 $ .所以 $ b=±2 $ ,即 $ z=2±2\mathrm{i} $ ,故 $ \dfrac{\overline{z}}{z}=±\mathrm{i} $ .

设 $ {z}_{1} $ , $ {z}_{2} $ 在复平面内对应的向量分别为 $ \boldsymbol{a} $ , $ \boldsymbol{b} $ ,则 $ |\boldsymbol{a}|=2 $ , $ |\boldsymbol{b}|=1 $ ,且 $ \boldsymbol{a}+\boldsymbol{b}=(1,2) $ .

考虑到 $ (\boldsymbol{a}+\boldsymbol{b})^{2}+(\boldsymbol{a}-\boldsymbol{b})^{2}=2|\boldsymbol{a}{|}^{2}+2|\boldsymbol{b}{|}^{2} $ ,故 $ 5+(\boldsymbol{a}-\boldsymbol{b})^{2}=10 $ ,

故 $ |\boldsymbol{a}-\boldsymbol{b}|=\sqrt{5} $ ,所以 $ |{z}_{1}-{z}_{2}|=\sqrt{5} $ .

由题意将 $ \left|\begin{matrix}z1+\mathrm{i}\\ -\mathrm{i}2\mathrm{i}\end{matrix}\right|=0 $ 化简得, $ z\cdot 2\mathrm{i}+\mathrm{i}(1+\mathrm{i})=0 $ , $ z=\dfrac{1-\mathrm{i}}{2\mathrm{i}}=\dfrac{\mathrm{i}-{\mathrm{i}}^{2}}{2{\mathrm{i}}^{2}}=\dfrac{\mathrm{i}+1}{-2}=-\dfrac{1}{2}-\dfrac{1}{2}\mathrm{i} $ ,所以 $ \overline{z}=-\dfrac{1}{2}+\dfrac{1}{2}\mathrm{i} $ ,所以复数 $ \overline{z} $ 在复平面内对应的点在第二象限.

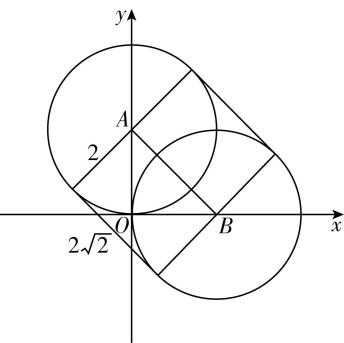
如图,在复平面内,设 $ {z}_{1} $ 对应的点为 $ P $ ,则点 $ P $ 在线段 $ AB $ 上运动,其中 $ A(0,2) $ , $ B(2,0) $ , $ |AB|=2\sqrt{2} $ .

设 $ {z}_{2} $ 对应的点为 $ Q $ ,则点 $ Q $ 在以原点为圆心的单位圆上运动, $ |OQ|=1 $ .

设 $ {z}_{1}+2{z}_{2} $ 对应的点为 $ M $ ,则 $ \overrightarrow {OM}=\overrightarrow {OP}+2\overrightarrow {OQ} $ ,所以 $ |\overrightarrow {OM}-\overrightarrow {OP}|=2|\overrightarrow {OQ}|=2 $ ,则 $ |\overrightarrow {PM}|=2 $ ,

即点 $ M $ 在以点 $ P $ 为圆心,2为半径的圆上运动.

当点 $ P $ 在线段 $ AB $ 上运动时,点 $ M $ 在复平面上扫过的图形为一个矩形（长和宽分别为4和 $ 2\sqrt{2} $ ）和两个半圆（半径为2）,

其面积为 $ 4×2\sqrt{2}+\mathrm{\pi }×{2}^{2}=8\sqrt{2}+4\mathrm{\pi } $ .