1．下列说法正确的是（ ）
A．有两个面平行，其余各面都是四边形的几何体叫棱柱
B．有两个面平行，其余各面都是平行四边形的几何体叫棱柱
C．各侧面都是正方形的四棱柱一定是正方体
D．九棱柱有9条侧棱，9个侧面，侧面均为平行四边形
有两个面平行,其余各面是四边形，且每相邻两个四边形的公共边都相互平行的几何体叫棱柱,满足 $ \mathrm{A} $ 选项或 $ \mathrm{B} $ 选项描述的一种几何体如图所示,故 $ \mathrm{A} $ , $ \mathrm{B} $ 都不正确.
各侧面都是正方形的四棱柱,上下底面可能是菱形,故 $ \mathrm{C} $ 不正确.
根据棱柱的定义可知九棱柱有9条侧棱,9个侧面,侧面均为平行四边形，故 $ \mathrm{D} $ 正确.故选 $ \mathrm{D} $ .
2．（多选）下列命题中为假命题的是（ ）（多选）
A．长方体是四棱柱，直四棱柱是长方体
B．棱柱中至少有两个面的形状完全相同
C．有两个侧面是矩形的四棱柱是直四棱柱
D．正四棱柱是平行六面体
对于选项 $ \mathrm{A} $ ,当底面不是矩形的时候,直四棱柱非长方体, $ \mathrm{A} $ 为假命题；对于选项 $ \mathrm{B} $ ,棱柱的两个底面全等,则棱柱中至少有两个面的形状完全相同, $ \mathrm{B} $ 为真命题；对于选项 $ \mathrm{C} $ ,有两个侧面是矩形的四棱柱可以是两对称面为矩形的平行六面体, $ \mathrm{C} $ 为假命题； $ \mathrm{D} $ 选项,正四棱柱是平行六面体, $ \mathrm{D} $ 为真命题.故选 $ \mathrm{A}\mathrm{C} $ .
3．如图所示，在三棱台 $ A^\prime B^\prime C^\prime -ABC $ 中，截去三棱锥 $ A^\prime -ABC $ ，则剩余部分是（ ）
A．三棱锥
B．四棱锥
C．三棱柱
D．组合体
三棱台 $ A^\prime B^\prime C^\prime -ABC $ 中，沿平面 $ A^\prime BC $ 截去三棱锥 $ A^\prime -ABC $ ，剩余的部分是以 $ A^\prime $ 为顶点，四边形 $ BCC\prime B^\prime $ 为底面的四棱锥 $ A^\prime -BCC\prime B^\prime $ .故选 $ \mathrm{B} $ .
4．（多选）下列说法中正确的有（ ）（多选）
A．正四面体是正三棱锥
B．棱锥的侧面是全等的三角形
C．正三棱锥是正四面体
D．延长棱台所有侧棱，它们会交于一点
$ \mathrm{A} $ 选项,正四面体的四个面都是等边三角形,是正三棱锥, $ \mathrm{A} $ 正确；
$ \mathrm{B} $ 选项,棱锥的侧面是三角形,不一定全等, $ \mathrm{B} $ 错误；
$ \mathrm{C} $ 选项,正三棱锥的侧棱长和底面边长不一定相等, $ \mathrm{C} $ 错误；
$ \mathrm{D} $ 选项,根据棱台的定义可知,延长棱台所有侧棱,它们会交于一点, $ \mathrm{D} $ 正确.故选 $ \mathrm{A}\mathrm{D} $ .
5．（多选）下列说法中，不正确的是（ ）（多选）
A．有两个面互相平行，其余四个面都是等腰梯形的六面体是棱台
B．有一个面是多边形，其余各面都是三角形的几何体是棱锥
C．棱锥至少有6条棱
D．若棱锥的侧棱长与底面多边形的边长相等，则此棱锥可能是正三棱锥
对于 $ \mathrm{A} $ ,有两个面互相平行,其余四个面都是等腰梯形的六面体不一定是棱台,如图①.只有当四个等腰梯形的腰延长后交于一点,这个六面体才是棱台,故 $ \mathrm{A} $ 错误.
图①
对于 $ \mathrm{B} $ ,有一个面是多边形,其余各面都是三角形的几何体不一定是棱锥,如图②,故 $ \mathrm{B} $ 错误.
图②
对于 $ \mathrm{C} $ ,三棱锥是棱数最少的棱锥,有6条棱,故 $ \mathrm{C} $ 正确.
对于 $ \mathrm{D} $ ,棱锥的侧棱长与底面多边形的边长相等,若底面是正三角形,则此棱锥是正三棱锥,故 $ \mathrm{D} $ 正确.故选 $ \mathrm{A}\mathrm{B} $ .
6．如图是一个正方体的表面展开图，则图中“九”在正方体中的对面是（ ）
A．县
B．市
C．联
D．考
把正方体还原后如图所示,
则上面是九,下面是市,左面是县,右面是联,前面是考,后面是区,故选 $ \mathrm{B} $ .
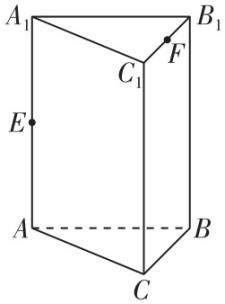
7．如图所示，在直三棱柱 $ ABC-{A}_{1}{B}_{1}{C}_{1} $ 中， $ AB=BC=2 $ ， $ B{B}_{1}=2\sqrt{2} $ ， $ \mathrm{\angle }ABC={90}^{\circ } $ ， $ E $ ， $ F $ 分别是 $ A{A}_{1} $ ， $ {B}_{1}{C}_{1} $ 的中点，沿棱柱表面从 $ E $ 到 $ F $ 的最短路径长为（ ）
A． $ \sqrt{11} $
B． $ \sqrt{7+2\sqrt{2}} $
C．3
D． $ \sqrt{7+\sqrt{2}} $
若从 $ E $ 到 $ F $ 经过棱 $ {A}_{1}{B}_{1} $ ，则沿棱 $ {A}_{1}{B}_{1} $ 展开如图①，
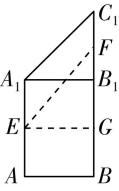
图①
过 $ E $ 作 $ EG\perp B{B}_{1} $ 于 $ G $ ，则 $ EG=AB=2 $ ， $ FG=1+\sqrt{2} $ ，
故 $ EF=\sqrt{{2}^{2}+(1+\sqrt{2})^{2}}=\sqrt{7+2\sqrt{2}} $ .
若从 $ E $ 到 $ F $ 经过棱 $ B{B}_{1} $ ，则沿棱 $ B{B}_{1} $ 展开如图②， $ {A}_{1}E=\sqrt{2} $ ， $ {A}_{1}F=3 $ ，则 $ EF=\sqrt{(\sqrt{2})^{2}+{3}^{2}}=\sqrt{11} $ .
图②
若从 $ E $ 到 $ F $ 经过棱 $ C{C}_{1} $ ，则沿棱 $ C{C}_{1} $ 展开如图③，因为 $ AB=BC=2 $ ， $ \mathrm{\angle }ABC={90}^{\circ } $ ，
图③
所以 $ AC=\sqrt{{2}^{2}+{2}^{2}}=2\sqrt{2} $ ，
$ {A}_{1}E=\sqrt{2} $ ， $ {A}_{1}F=2\sqrt{2}+1 $ ，则 $ EF=\sqrt{2+(2\sqrt{2}+1)^{2}}=\sqrt{11+4\sqrt{2}} $ .
若从 $ E $ 到 $ F $ 经过棱 $ {A}_{1}{C}_{1} $ ，则沿棱 $ {A}_{1}{C}_{1} $ 展开如图④，连接 $ A{C}_{1} $ ，由题意， $ △{A}_{1}{B}_{1}{C}_{1} $ 为等腰直角三角形，四边形 $ AC{C}_{1}{A}_{1} $ 为正方形，故 $ △{A}_{1}A{C}_{1} $ 为等腰直角三角形，故四边形 $ {A}_{1}{B}_{1}{C}_{1}A $ 为直角梯形.
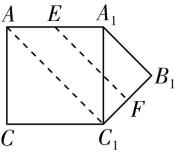
图④
又 $ {A}_{1}{B}_{1}=2 $ ， $ A{C}_{1}=\sqrt{(2\sqrt{2})^{2}+(2\sqrt{2})^{2}}=4 $ ，故 $ EF=\dfrac{1}{2}×(2+4)=3 $ .
又 $ 3=\sqrt{9} < \sqrt{7+2\sqrt{2}} < \sqrt{11} < \sqrt{11+4\sqrt{2}} $ ，所以沿棱柱表面从 $ E $ 到 $ F $ 的最短路径长为3.故选 $ \mathrm{C} $ .
8．现有一块如图所示的三棱锥木料，其中 $ \mathrm{\angle }AVB=\mathrm{\angle }AVC=\mathrm{\angle }BVC={40}^{\circ } $ ， $ VA=VB=VC=6 $ ，木工师傅打算过点 $ A $ 将木料切成两部分，则截面 $ △AEF $ 周长的最小值为 .
$ 6\sqrt{3} $
将三棱锥的侧面沿着 $ VA $ 展开,连接 $ A^\prime A $ ,如图所示.
则 $ VA=VA\prime =6 $ , $ \mathrm{\angle }AVA\prime ={120}^{\circ } $ ,
由余弦定理可得, $ AA{\prime }^{2}={6}^{2}+{6}^{2}-2×6×6 \cos {120}^{\circ }=108 $ ,则 $ AA\prime =6\sqrt{3} $ ,
所以截面 $ △AEF $ 周长的最小值为 $ 6\sqrt{3} $ .