8.1课时2 圆柱、圆锥、圆台和球

以矩形的一边所在的直线为旋转轴,将矩形旋转一周而形成的曲面所围成的几何体叫做圆柱,以矩形的一条对角线所在直线为轴,旋转所得到的几何体不是圆柱,故 $ \mathrm{A} $ 错误；

圆锥的顶点、圆锥底面圆周上任意一点及底面圆的圆心三点的连线可以构成直角三角形,故 $ \mathrm{B} $ 正确；

用一平行于底面的平面去截圆锥,底面与截面之间的部分叫做圆台,故 $ \mathrm{C} $ 错误；

通过圆台侧面上一点,只能作一条母线,故 $ \mathrm{D} $ 错误.故选 $ \mathrm{B} $ .

因为等腰梯形上、下底边互相平行,两腰相等,所以以较长的底边所在直线为轴,其他三边旋转一周形成的面所围成的几何体的几何结构是一个圆柱、两个圆锥,故选 $ \mathrm{A} $ .

对于①,根据圆柱的特征,可知①正确；

对于②,圆锥的轴截面为等腰三角形,该三角形顶角的取值范围为 $ (0,\mathrm{\pi }) $ ,若三角形的顶角不相等,则三角形的面积可能不相等,故②错误；

对于③,根据圆台的特征,可知③正确；

对于④,圆锥所有的轴截面都是等腰三角形,且腰长等于母线长,底长等于圆锥底面圆直径,故④正确.

故错误的说法为②.

由题意,圆柱的侧面展开图是矩形,如图所示, $ AC $ 即为葛藤的最短长度,一条直角边长（即圆木的高）为 $ 3×10+5=35 $ （尺）,另一条直角边长为 $ 3×4=12 $ （尺）,故葛藤的最短长度为 $ \sqrt{{35}^{2}+{12}^{2}}=37 $ （尺）.故选 $ \mathrm{A} $ .

由圆锥底面半径为 $ \sqrt{2} $ ,侧面展开图是圆心角为 $ \dfrac{2\mathrm{\pi }}{3} $ 的扇形,可设圆锥的母线长为 $ l $ ,则 $ l=\dfrac{2\mathrm{\pi }×\sqrt{2}}{\dfrac{2\mathrm{\pi }}{3}}=3\sqrt{2} $ .

连接 $ AE $ ,将 $ △ABE $ 绕直线 $ AB $ 旋转到 $ △PAB $ 的位置,并且点 $ P $ 在 $ BC $ 的反向延长线上,连接 $ PG $ ,交 $ AB $ 于点 $ F $ ,此时 $ EF+FG $ 最小,最小值为 $ PG $ ,如图所示.

因为 $ AB=BC=2 $ ,所以 $ \mathrm{\angle }ACB=\mathrm{\angle }PCG=\dfrac{\mathrm{\pi }}{4} $ .又因为 $ BC=2BE $ ,所以 $ BE=BP=1 $ ,

又 $ AC=\sqrt{2}AB=2\sqrt{2} $ ,

所以 $ CG=\dfrac{3}{4}AC=\dfrac{3\sqrt{2}}{2} $ , $ PC=PB+BC=3 $ .

在 $ △PCG $ 中,由余弦定理得 $ P{G}^{2}=P{C}^{2}+C{G}^{2}-2PC\cdot CG\cdot \cos \mathrm{\angle }PCG=9+\dfrac{9}{2}-2×3×\dfrac{3\sqrt{2}}{2}×\dfrac{\sqrt{2}}{2}=\dfrac{9}{2} $ ,解得 $ PG=\dfrac{3\sqrt{2}}{2} $ ,即 $ EF+FG $ 的最小值为 $ \dfrac{3\sqrt{2}}{2} $ .

对于 $ \mathrm{A} $ ,如图①,用平面 $ AC{D}_{1} $ 截长方体 $ ABCD-{A}_{1}{B}_{1}{C}_{1}{D}_{1} $ ,得到的截面是三角形,故 $ \mathrm{A} $ 正确；

图①

对于 $ \mathrm{B} $ ,如图②,用平面 $ PAB $ 截圆锥,得到的截面是三角形,故 $ \mathrm{B} $ 正确；

图②

对于 $ \mathrm{C} $ ,三棱锥各个面为三角形,除三棱锥外,过棱锥底面不相邻两顶点和棱锥顶点的截面为三角形,故 $ \mathrm{C} $ 正确；

对于 $ \mathrm{D} $ ,圆台的截面不可能为三角形,故 $ \mathrm{D} $ 错误.故选 $ \mathrm{D} $ .

由题图可知,扇形的弧长等于圆锥底面圆的周长,且圆锥底面圆的半径 $ r=1 $ .

设扇形半径为 $ R $ ,则有 $ \dfrac{\mathrm{\pi }}{2}R=2\mathrm{\pi }r $ ,解得 $ R=4 $ ,所以圆锥的母线长 $ R=4 $ ,

故圆锥的高 $ h=\sqrt{{R}^{2}-{r}^{2}}=\sqrt{16-1}=\sqrt{15} $ .

故选 $ \mathrm{C} $ .

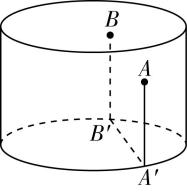
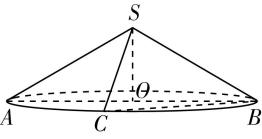
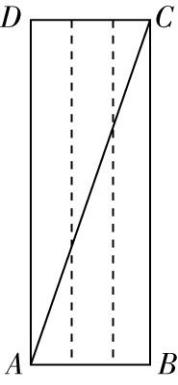
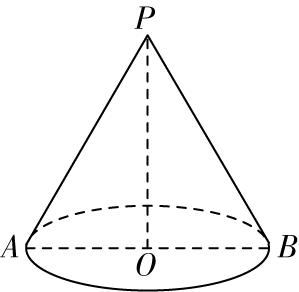
对于 $ \mathrm{A} $ ,圆台的高即轴截面等腰梯形 $ ABCD $ 的高 $ h=\sqrt{{2}^{2}-(2-1)^{2}}=\sqrt{3} $ ,因此圆台的轴截面面积为 $ \dfrac{2+4}{2}×\sqrt{3}=3\sqrt{3} $ , $ \mathrm{A} $ , $ \mathrm{B} $ 正确.

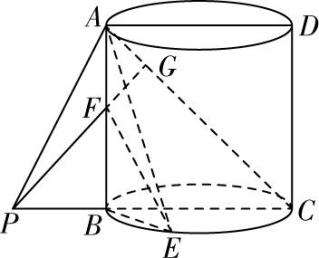
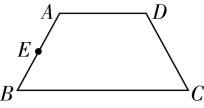
对于 $ \mathrm{C} $ ,如图,延长 $ BA $ , $ CD $ 交于点 $ F $ ,则 $ \dfrac{FA}{FA+AB}=\dfrac{{r}_{1}}{{r}_{2}}=\dfrac{1}{2} $ ,解得 $ FA=2 $ .

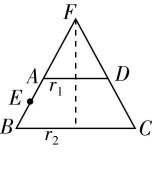
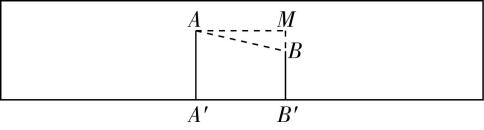
如图,将圆台的侧面展开，设圆台的侧面所在扇形的圆心角为 $ \alpha $ ，圆台的上底面周长为 $ 2\mathrm{\pi } $ ,下底面周长为 $ 4\mathrm{\pi } $ ,则 $ \alpha =\dfrac{2\mathrm{\pi }}{2}=\mathrm{\pi } $ ,故圆台侧面展开图是半圆环,则圆台的侧面积为 $ \dfrac{1}{2}\cdot 4\mathrm{\pi }\cdot 4-\dfrac{1}{2}\cdot 2\mathrm{\pi }\cdot 2=6\mathrm{\pi } $ , $ \mathrm{C} $ 错误.

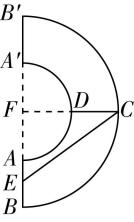
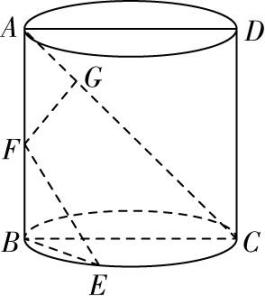
在圆台的侧面上,从点 $ C $ 到点 $ E $ 的最短路径的长度为线段 $ CE $ 的长度,

由题意得, $ FB=FC=4 $ , $ AB=2 $ ,由 $ E $ 为 $ AB $ 的中点,得 $ FE=3 $ ,

所以 $ CE=\sqrt{C{F}^{2}+F{E}^{2}}=\sqrt{{4}^{2}+{3}^{2}}=5 $ , $ \mathrm{D} $ 正确.故选 $ \mathrm{A}\mathrm{B}\mathrm{D} $ .

用一个平面去截圆锥得到的截面可能为三角形、圆等,不可能出现矩形,故 $ \mathrm{A} $ 不满足题意；

用一个平行于底面的平面去截正四棱锥得到的截面为正方形（也是矩形）,故 $ \mathrm{C} $ 满足题意；

用一个平面去截圆柱、正方体,截面的形状都有可能是矩形,故 $ \mathrm{B} $ , $ \mathrm{D} $ 满足题意.故选 $ \mathrm{B}\mathrm{C}\mathrm{D} $ .

对于 $ \mathrm{A} $ ,圆柱的侧面展开图是矩形,所以 $ \mathrm{A} $ 正确；对于 $ \mathrm{B} $ ,球面可以看成是一个圆绕着它的直径所在的直线旋转 $ {180}^{\circ } $ 所形成的曲面,所以 $ \mathrm{B} $ 正确；对于 $ \mathrm{C} $ ,直角梯形只有在绕它垂直于底边的腰所在直线旋转一周形成的几何体才是圆台,所以 $ \mathrm{C} $ 错误；对于 $ \mathrm{D} $ ,圆柱、圆锥、圆台中,平行于底面的截面都是圆面,所以 $ \mathrm{D} $ 正确.故选 $ \mathrm{A}\mathrm{B}\mathrm{D} $ .

由题知圆台上、下底面半径分别为 $ {r}_{1}=1 $ , $ {r}_{2}=2 $ .设母线长为 $ l $ ,高为 $ h $ ,则球 $ O $ 的直径为 $ h $ ,因为 $ BC $ 与半圆 $ O $ 相切于点 $ P $ ,则 $ BP={r}_{1}=1 $ , $ CP={r}_{2}=2 $ ,所以 $ l=BP+CP=3 $ ,①正确.

过点 $ B $ 作 $ BM\perp CD $ 于点 $ M $ ,则 $ BM=h $ , $ CM={r}_{2}-{r}_{1}=1 $ ,所以 $ h=\sqrt{{l}^{2}-C{M}^{2}}=\sqrt{{3}^{2}-{1}^{2}}=2\sqrt{2} $ ,即球 $ O $ 的半径为 $ \sqrt{2} $ ,②正确.

因为 $ AB//CD $ ,易得 $ \dfrac{HA}{HD}=\dfrac{AB}{CD}=\dfrac{1}{2} $ ,则 $ HD=2HA=2AD=2h=4\sqrt{2} $ , $ ③ $ 错误.

过点 $ P $ 作 $ PQ\perp BM $ 于点 $ Q $ ,延长 $ PQ $ 与 $ AD $ 交于点 $ {O}_{1} $ ,则 $ P $ 的轨迹是以 $ {O}_{1} $ 为圆心, $ {O}_{1}P $ 为半径的圆.

作 $ PN\perp CD $ 于点 $ N $ ,得 $ △BQP\sim △PNC $ ,则 $ \dfrac{BP}{PC}=\dfrac{QP}{NC} $ ,即 $ \dfrac{1}{2}=\dfrac{{O}_{1}P-1}{2-DN}=\dfrac{{O}_{1}P-1}{2-{O}_{1}P} $ ,解得 $ {O}_{1}P=\dfrac{4}{3} $ .所以点 $ P $ 的轨迹的长度是 $ 2\mathrm{\pi }×\dfrac{4}{3}=\dfrac{8\mathrm{\pi }}{3} $ ,④错误.故选 $ \mathrm{B} $ .

过正方体中心的平面截正方体所得的截面至少与正方体的四个面相交,所以不可能是三角形；截面为五边形时不过正方体的中心；过正方体各面上相邻两边的中点以及正方体的中心的截面图形为正六边形.故答案为②④.

不妨设 $ a > b $ .该圆柱的侧面展开图如图所示,过 $ A $ 作 $ A^\prime B^\prime $ 的平行线,交 $ B^\prime B $ 的延长线于 $ M $ .已知 $ AA\prime =a $ , $ BB\prime =b $ ,则 $ MB=a-b $ , $ \stackrel{⌢}{A^\prime B^\prime }=\dfrac{\mathrm{\pi }R}{3}=AM $ ,沿圆柱侧面从 $ A $ 到 $ B $ 的最短距离是 $ AB $ .根据勾股定理可得 $ AB=\sqrt{A{M}^{2}+M{B}^{2}}=\sqrt{ (a-b)^{2}+{\left(\dfrac{\mathrm{\pi }R}{3} \right) ^ {2}}} $ .

由 $ {S}_{△SAB}=\dfrac{1}{2}SO\cdot AB=2\sqrt{3}SO=4\sqrt{3} $ ,即 $ SO=2 $ ,故 $ SA=SB=\sqrt{{2}^{2}+(2\sqrt{3})^{2}}=4 $ .

令 $ \mathrm{\angle }ASB=2\theta $ 且 $ 0 < \theta < \dfrac{\mathrm{\pi }}{2} $ ,则 $ \sin \theta =\dfrac{OB}{SB}=\dfrac{2\sqrt{3}}{4}=\dfrac{\sqrt{3}}{2} $ ,即 $ \theta =\dfrac{\mathrm{\pi }}{3} $ ,所以 $ \mathrm{\angle }ASB=\dfrac{2\mathrm{\pi }}{3} $ .

由 $ {S}_{△SBC}=\dfrac{1}{2}SB\cdot SC \sin \mathrm{\angle }BSC=8 \sin \mathrm{\angle }BSC $ ,而 $ 0 < \mathrm{\angle }BSC\leqslant \dfrac{2\mathrm{\pi }}{3} $ ,

所以当 $ \mathrm{\angle }BSC=\dfrac{\mathrm{\pi }}{2} $ 时,截面 $ SBC $ 的面积最大,此时 $ {S}_{△SBC}=8 $ .

对于 $ \mathrm{A} $ ：圆台的上、下底面的圆周上各取一点,这两点的连线不一定是母线,因为圆台所有母线的延长线交于一点,且所有母线长相等,故 $ \mathrm{A} $ 错误；

对于 $ \mathrm{B} $ ：如图,四面体 $ A-BCD $ 的每个面都是直角三角形,故 $ \mathrm{B} $ 正确；

对于 $ \mathrm{C} $ ：半圆面绕其直径所在的直线旋转一周得到的几何体是球,故 $ \mathrm{C} $ 正确；

对于 $ \mathrm{D} $ ：球面上两点与球心共线时,连成的线段才是球的直径,故 $ \mathrm{D} $ 错误.故选 $ \mathrm{B}\mathrm{C} $ .

选项 $ \mathrm{A} $ 是圆锥的性质,故 $ \mathrm{A} $ 正确；对于 $ \mathrm{B} $ ,一张扇形的纸片只能卷成一个无底面的圆锥,故 $ \mathrm{B} $ 错误；对于 $ \mathrm{C} $ ,根据圆柱的结构特征可知,若两个相等的圆面不平行,那么这个几何体不是圆柱,故 $ \mathrm{C} $ 错误；对于 $ \mathrm{D} $ ,圆台是由圆锥截得的,所以其任意两条母线延长后一定交于一点,故 $ \mathrm{D} $ 错误.故选 $ \mathrm{A} $ .

设两个截面圆的半径分别为 $ {r}_{1} $ , $ {r}_{2} $ ,则 $ \mathrm{\pi }{r}_{1}^{2}=10\mathrm{\pi } $ , $ \mathrm{\pi }{r}_{2}^{2}=7\mathrm{\pi } $ ,解得 $ {r}_{1}=\sqrt{10} $ , $ {r}_{2}=\sqrt{7} $ .设两个截面到球心的距离分别为 $ {d}_{1} $ , $ {d}_{2} $ ,则 $ {d}_{1}=\sqrt{16-10}=\sqrt{6} $ , $ {d}_{2}=\sqrt{16-7}=3 $ ,故这两个平面之间的距离为 $ 3-\sqrt{6} $ 或 $ 3+\sqrt{6} $ .