1.如图所示的几何体是一个奖杯,该几何体由( )
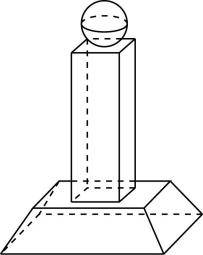
A.一个球、一个四棱柱、一个圆台构成
B.一个球、一个长方体、一个棱台构成
C.一个球、一个四棱台、一个圆台构成
D.一个球、一个五棱柱、一个棱台构成
由题图可知,该几何体是由一个球、一个长方体、一个棱台构成.故选 $ \mathrm{B} $ .
1.如图所示的几何体是一个奖杯,该几何体由( )

A.一个球、一个四棱柱、一个圆台构成
B.一个球、一个长方体、一个棱台构成
C.一个球、一个四棱台、一个圆台构成
D.一个球、一个五棱柱、一个棱台构成
由题图可知,该几何体是由一个球、一个长方体、一个棱台构成.故选 $ \mathrm{B} $ .
2.已知正五边形 $ ABCDE $ 的中心为 $ O $ .以 $ AO $ 所在的直线为轴,其余五边旋转半周形成的面围成一个几何体,则( )
A.该几何体为圆台
B.该几何体是由圆台和圆锥组合而成的简单组合体
C.该几何体为圆柱
D.该几何体是由圆柱和圆锥组合而成的简单组合体
画出正五边形 $ ABCDE $ ,以 $ AO $ 所在的直线为轴,其余五边旋转半周形成的面所围成的几何体如图所示,

由图可知,该几何体是由圆台和圆锥组合而成的简单组合体.故选 $ \mathrm{B} $ .
3.某广场设置了一些石凳供大家休息,如图,每个石凳都是由正方体截去八个相同的正三棱锥得到的几何体,则下列结论不正确的是( )
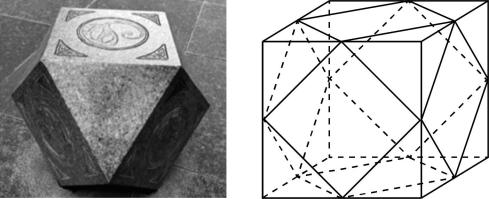
A.该几何体有6个面是正方形
B.该几何体有8个面是正三角形
C.该几何体恰有26条棱
D.该几何体的表面积比原正方体的表面积小
对于 $ \mathrm{A} $ , $ \mathrm{B} $ ,因为正方体截去八个正三棱锥,所以比原正方体多出八个正三角形,原来的六个表面还是正方形,所以 $ \mathrm{A} $ , $ \mathrm{B} $ 正确;
对于 $ \mathrm{C} $ ,因为原正方体每个表面均有四条棱,所以该几何体共有24条棱, $ \mathrm{C} $ 不正确;
对于 $ \mathrm{D} $ ,不妨取正方体的棱长为2,截去的每个正三棱锥的侧面积为 $ 3×\dfrac{1}{2}×1×1=\dfrac{3}{2} $ ,
而它的底面是边长为 $ \sqrt{2} $ 的正三角形,其面积为 $ \dfrac{1}{2}×(\sqrt{2})^{2}×\dfrac{\sqrt{3}}{2}=\dfrac{\sqrt{3}}{2} < \dfrac{3}{2} $ ,
即截去的每个正三棱锥的侧面积比底面积大,所以该几何体的表面积比原正方体的表面积小,所以 $ \mathrm{D} $ 正确.故选 $ \mathrm{C} $ .
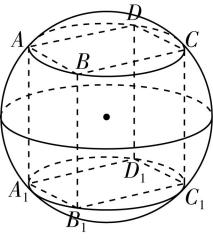
4.如图所示的几何体为一个球挖去一个内接正方体得到的组合体,现用一个过球心的平面截它,所得截面图形不可能是( )
A.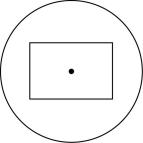
B.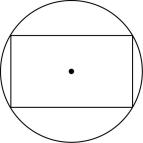
C.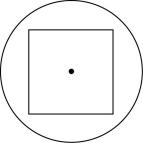
D.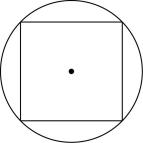
当截面过球心,且截面不平行于正方体的每个面,不过体对角线时,截面图形是 $ \mathrm{A} $ ;
当截面过正方体的对角面时,截面图形是 $ \mathrm{B} $ ;
当截面过球心,且平行于正方体的一个面时,截面图形是 $ \mathrm{C} $ ;
过球心的截面不能为 $ \mathrm{D} $ .故选 $ \mathrm{D} $ .
5.一个长方体的容器中装有一定量的水,现在将容器绕着其底部的一条棱旋转,在旋转的过程中,
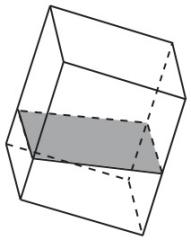
(1) 水面的形状不断变化,可能是矩形,也可能变成不是矩形的平行四边形,对吗?
(2) 水的形状也不断变化,可以是棱柱,也可能变为棱台或棱锥,对吗?
(3) 如果旋转时,不是绕着底部的一条棱,而是绕着其底面的一个顶点,上面的第(1)问和第(2)问对不对?
(1) 【解】不对.水面的形状就是用一个与旋转时固定不动的棱平行的平面截长方体时截面的形状,因而是矩形,不可能是非矩形的平行四边形.
(2) 不对.水的形状就是用与旋转时固定不动的棱平行的平面将长方体截去一部分后,剩余部分的几何体,此几何体是棱柱.水比较少时,是三棱柱;水较多时,可能是四棱柱或五棱柱,但不可能是棱台或棱锥.
(3) 用任意一个过长方体底面的一个顶点的平面去截长方体,其截面形状可以是三角形、四边形、五边形、六边形,因而水面的形状可以是三角形、四边形、五边形、六边形;水的形状可以是棱锥、棱柱、棱台.故此时(1)对,(2)对.
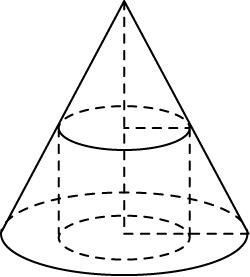
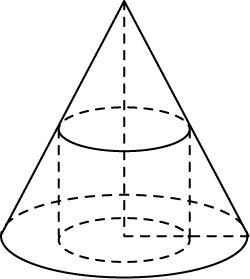
6.如图,在底面半径为2,母线长为4的圆锥中内接一个高为 $ \sqrt{3} $ 的圆柱,则圆锥过轴的截面面积为 ,圆柱的底面半径为 .
$ 4\sqrt{3} $ ; 1
如图,圆锥的高 $ h=\sqrt{{4}^{2}-{2}^{2}}=2\sqrt{3} $ ,则圆锥过轴的截面面积为 $ \dfrac{1}{2}×4×2\sqrt{3}=4\sqrt{3} $ .
设圆柱的底面半径为 $ r $ ,由相似三角形的知识可得 $ \dfrac{r}{2}=\dfrac{2\sqrt{3}-\sqrt{3}}{2\sqrt{3}} $ ,解得 $ r=1 $ ,即圆柱的底面半径为1.