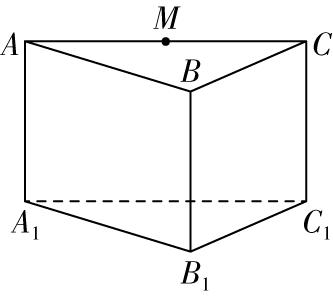
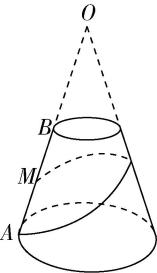
5.如图,在底面为正三角形的直三棱柱 $ ABC-{A}_{1}{B}_{1}{C}_{1} $ 中, $ AB=2\sqrt{3} $ , $ A{A}_{1}=2 $ ,点 $ M $ 为 $ AC $ 的中点,一只小虫从 $ {B}_{1} $ 沿三棱柱 $ ABC-{A}_{1}{B}_{1}{C}_{1} $ 的表面爬行到 $ M $ 处,则小虫爬行的最短路程为 .
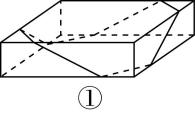
解析:如图①,将三棱柱 $ ABC-{A}_{1}{B}_{1}{C}_{1} $ 的侧面 $ B{B}_{1}{C}_{1}C $ 和侧面 $ C{C}_{1}{A}_{1}A $ 沿 $ C{C}_{1} $ 展开至同一平面内,连接 $ M{B}_{1} $ ,
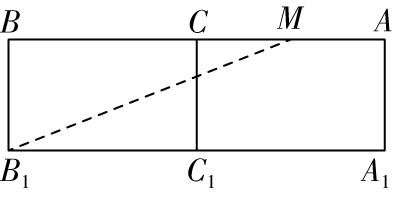
图①
$ \because M $ 为 $ AC $ 的中点,直三棱柱底面 $ △ABC $ 和 $ △{A}_{1}{B}_{1}{C}_{1} $ 是等边三角形,
$ \therefore CM=\dfrac{1}{2}AC=\sqrt{3} $ , $ \therefore BM=CM+BC=3\sqrt{3} $ ,
在 $ \mathrm{R}\mathrm{t}△MB{B}_{1} $ 中,由勾股定理得 $ {B}_{1}M=\sqrt{31} $ .
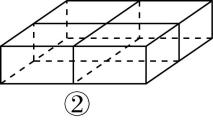
如图②,把底面 $ ABC $ 和侧面 $ B{B}_{1}{A}_{1}A $ 沿 $ AB $ 展开至同一平面内,连接 $ M{B}_{1} $ ,
过点 $ M $ 作 $ MF\perp {A}_{1}{B}_{1} $ 于点 $ F $ ,交 $ AB $ 于点 $ E $ ,由图易知四边形 $ AEF{A}_{1} $ 是矩形,且 $ ME\perp AB $ ,
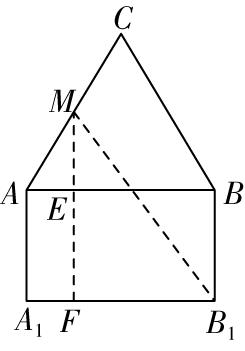
图②
在 $ \mathrm{R}\mathrm{t}△AME $ 中, $ \mathrm{\angle }MAE={60}^{\circ } $ ,
$ \therefore ME=AM\cdot \sin {60}^{\circ }=\sqrt{3}×\dfrac{\sqrt{3}}{2}=\dfrac{3}{2} $ , $ AE=AM\cdot \cos {60}^{\circ }=\dfrac{\sqrt{3}}{2} $ ,
$ \therefore MF=ME+EF=\dfrac{7}{2} $ , $ {B}_{1}F={A}_{1}{B}_{1}-{A}_{1}F=\dfrac{3\sqrt{3}}{2} $ ,
在 $ \mathrm{R}\mathrm{t}△MF{B}_{1} $ 中,由勾股定理可得 $ {B}_{1}M=\sqrt{19} $ .
如图③,将底面 $ {A}_{1}{B}_{1}{C}_{1} $ 和侧面 $ {A}_{1}{C}_{1}CA $ 沿 $ {A}_{1}{C}_{1} $ 展开至同一平面内,连接 $ {B}_{1}M $ 交 $ {A}_{1}{C}_{1} $ 于点 $ N $ ,则 $ {B}_{1}M\perp AC $ , $ {B}_{1}N\perp {A}_{1}{C}_{1} $ ,
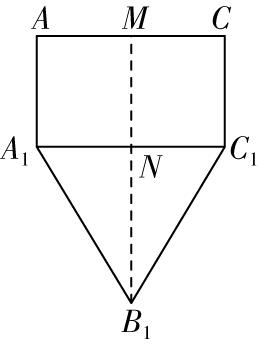
图③
$ 在\mathrm{R}\mathrm{t}△{A}_{1}N{B}_{1} $ 中, $ \mathrm{\angle }N{A}_{1}{B}_{1}={60}^{\circ } $ , $ \therefore N{B}_{1}={A}_{1}{B}_{1}\cdot \sin {60}^{\circ }=3 $ , $ \therefore {B}_{1}M={B}_{1}N+MN=5 $ .
$ \because \sqrt{19} < 5 < \sqrt{31} $ , $ \therefore $ 小虫爬行的最短路程为 $ \sqrt{19} $ .